基于互信息的深证股票复杂网络拓扑性质分析

胡振华,覃子龙,杨燕

(中南大学商学院,长沙410083)

基于互信息的深证股票复杂网络拓扑性质分析

胡振华,覃子龙,杨燕

(中南大学商学院,长沙410083)

文章针对以往在非线性系统中不当使用线性系统统计指标——Pearson相关系数来构建复杂网络的方法,以深证股票为研究对象,使用在非线性系统中衡量随机变量之间相关性的指标——互信息来构建复杂网络并分析了该网络的拓扑性质,认为深证股票复杂网络具有小世界特征和无标度特征,深证股票紧密程度高,市场信息传递效率也较高,社团结构呈现第二产业集聚、第三产业分散的特点,股票收益率的波动与产业链具有更大的相关性,网络对随机故障具有较高的鲁棒性,而对蓄意攻击具有高度的脆弱性。

非线性系统;信息熵;互信息;复杂网络;拓扑性质

0 引言

国内外大量的研究表明,金融市场具有参与要素众多、内部结构复杂等特点,在本质上是一个典型的非线性动力学系统,如收益率“尖峰厚尾”的分布特征、收益率波动的集聚现象等[1,2]。非线性理论对此提供了新的研究范式,其中网络科学把金融市场视为一个系统,认为系统内的个体是非匀质的,以异质的个体为节点,以个体之间存在的一定关系为边,构建出相应的复杂网络模型[3,4]。构建股票复杂网络模型主要采用两种方法:阈值法[5]和拓扑约束法[6],这两种方法均以Pearson相关系数为基础。在计算Pearson相关系数时,除了要求两个变量符合联合正态分布外,更要求两个变量之间呈直线相关关系。而股票收益率时间序列数据大多呈现出“尖峰厚尾”的特征,并不服从正态分布的假设;并且在上述方法中,以线性系统中的统计指标为基础来建立非线性系统模型,其适用性也值得商榷,可能产生潜在的估计错误风险。事实上,起源于信息论的互信息概念,可用于衡量非线性系统中两个或多个变量之间的相关关系,目前已经被广泛应用于生物基因、水文、经济等诸多领域。本文以信息熵和互信息为基础,以深证100指数为研究对象,阐明股票复杂网络模型的构建过程,并分析该复杂网络的拓扑性质。

1 信息熵和互信息

1.1 信息熵

信息熵的概念隶属于信息论领域,由热力学熵的概念泛化而来,Shannon首先定义了信息熵作为某件事情不确定性的度量。对于离散型随机变量X,其信息熵H(X)的定义式为:

其中,p(x)为x每种取值的概率,对于底数b的不同取值意味着信息熵H(X)有不同的量纲,以下不再赘述。对于连续型随机变量X,其信息熵H(X)的定义式为:

二维推广,对于离散型、连续型的随机变量X、y,分别有:

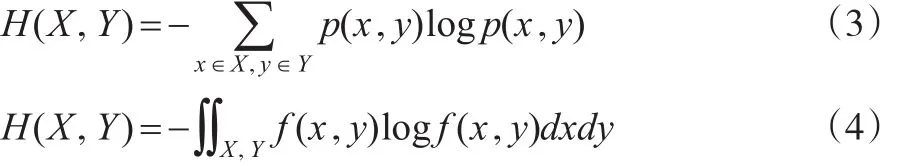
其中,p(x，y)为X、y的联合概率,f(x，y)为X、y的联合概率密度函数。

1.2 互信息

互信息用于度量两个或多个变量所共享的信息量,互信息越大则变量间的相关性越强,反之则反然。对于离散型、连续型的二维随机变量X、y,其定义式分别为:

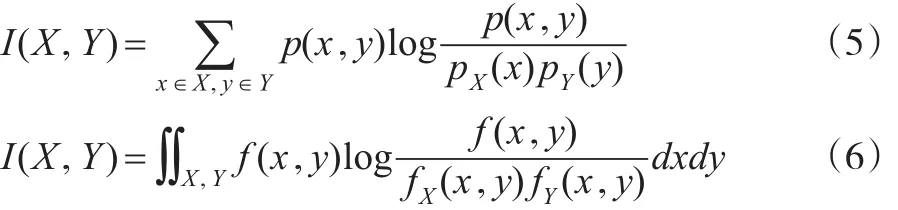
其中,pX(x)、py(y)分别为X、y的边缘概率, fX(x，y)、fy(x，y)分别为X、y的边缘概率密度函数。

根据上述公式,易得:

1.3 信息熵和互信息的估计

对信息熵和互信息的估计主要采用两种方法:参数方法和非参数方法。使用参数方法时,首先需假定概率密度函数的形式,再根据样本数据估计出其中的各项参数,进而求得信息熵和互信息。但在实际应用中,或者概率密度函数通常难以得知,或者参数方法无法处理非线性不规则的联合分布,使得参数方法的应用受到极大限制,而发展出的非参数方法得到更为广泛的应用。

常见的非参数方法有直方图法[7]和核函数法[8]。直方图法是把区间或者区域划分成若干个bin,进而估计概率密度函数,求得信息熵和互信息的方法。该方法简单易行,但精度较低,只适用于低维数据,计算误差主要来源于bin的数量的选择,换而言之,与bin的区间宽度h有关。核函数法是在每个样本点上叠置一个核函数,将所有核函数叠加而作为概率密度函数的一个估计,求得信息熵和互信息的方法。该方法计算复杂度高,精度也高,但只适用于小样本的情形,当样本量较大时,核参数的估计将会变得十分困难。值得一提的是,为了避免联合概率密度函数的估计,可以较为方便的通过Copula熵来估计互信息[9,10]。

2 基于互信息的深证股票复杂网络模型构建

鉴于时间序列的样本数据规模通常较大,本文舍弃核函数法估计信息熵和互信息;在将信息熵和互信息转换为欧氏空间距离时,为了保持分子、分母计算口径的一致性,本文舍弃了Copula熵法估计互信息,统一选用直方图法估计信息熵和互信息,进而构建相应的复杂网络。本文所有的数据处理和分析通过Matlab 7.11.0、Mathematica 9.0和Ucinet6实现。

2.1 数据来源与预处理

本文选取深证100指数作为分析对象,选取指标为每日收盘价。其中,深证100指数来自深圳证券交易所网站(http://www.szse.cn)发布的成分股,数据下载时间为2014年6月23日。股价数据的时间跨度为2011年1月4日至2014年3月31日,共783个观测日,74,895个观测数据,数据来源为锐思数据库(http://www.resset.cn)。对因上市时间较晚、停牌时间较长以及其他原因使得数据缺失较多的10支成分股数据予以剔除,对剩下90支股票的缺失数据采用线性插值法予以补齐。

2.2 构建股票复杂网络

(1)计算股票的对数收益率

其中,Rx(t)表示股票X第t期的对数收益率,px(t)表示股票X第t期的收盘价。

(2)采用等距法计算两两股票X、y的信息熵和互信息

①计算bin的最优宽度h*[11]

对于股票X,有:

其中,n为样本规模,σx为Rx的样本标准差,同理可得

②估计概率密度函数

构造Rx的M个bin区间设Rx落在区间上的样本点数量为ui,则有Rx的概率密度函数:

其中,N为Ry的bin区间数量,vi为Ry落在区间上的样本点数量,wij为Rx落在区间、Ry落在区间[ymin+(j-1)上的样本点数量。

③计算信息熵和互信息

依据式(2)、式(4)分别计算H(X)、H(y)和H(X，y),依据式(7)计算I(X，y)。

(3)计算欧氏距离

由于互信息不完全满足三角不等式,还需将其转换为欧氏空间距离d(X，y),计算公式为[12]:

(4)构建复杂网络

由于阈值法具有一定的主观性,并且阈值过低起不到良好的过滤冗余信息的效果;最小生成树的生成方法又存在信息过滤过度的问题;而平面最大过滤图不仅保留了最小生成树所包含的网络层级结构,还包含了网络内部结构的其他大量信息[13],因此本文使用平面最大过滤图来生成相应的复杂网络。

以股票为节点,以欧氏空间距离为边,设复杂网络共包含V个节点,以平面最大过滤图的方法来构建相应的复杂网络的步骤为[13]:初始网络不含任何连边,将d(X，y)按降序排列,逐次将d(X，y)所对应的边加入网络,当且仅当生成的网络仍是可平面图时加入该边,否则取消这条边的加入,直至网络包含3(V-2)条边,生成的深证股票平面最大过滤图PMFG如图1所示。

图1 深证股票复杂网络PMFG

3 深证股票复杂网络的拓扑性质分析

3.1 小世界特性

较多复杂网络都具有与相同规模随机网络相当的较小的平均路径长度,同时又具有与相同规模规则网络相当的较大的平均聚类系数,复杂网络所表现出的这种统计特性就是小世界特性。根据平面最大过滤图的生成规则, PMFG的平均度必然为以此为标准,生成相同规模的ER随机图和最近邻耦合网络,PMFG与它们的拓扑性质对比见表1。可以看到, PMFG既具有与ER随机图相近的平均路径长度,又具有与最近邻耦合网络相近的平均聚类系数,小世界特征十分明显。平均路径长度刻画了某个节点平均需要经过多少个节点即可到达另一个节点,PMFG较小的平均路径长度说明深证股票市场的信息传递效率较高;平均聚类系数刻画的是某个节点的任意两个邻居节点也互为邻居的可能性,PMFG较大的平均聚类系数说明深证股票的紧密程度较高。

表1 复杂网络PMFG和随机网络、规则网络的拓扑性质对比

3.2 无标度特性

不同于随机变量常见的钟形分布,大部分取值位于均值/峰值的附近,或者说落在以特征标度为中心的一个相对较小的区间里。现实中的很多复杂网络的大部分节点度都比较小,但也存在少数较大的节点度,即服从“长尾”分布,不存在单一的特征标度,这一统计特性就是复杂网络的无标度特性。如图2(a)所示,复杂网络PMFG的度分布很不均匀,大多数节点的度数都很小,一半以上股票的度数为2;但也有少量度数较大的Hub节点,节点度最高的股票是乐视网,度数达到66,也就是说,该股票与网络中近75%的股票有连接,存在相关关系。如图2(b)所示,在双对数直角坐标系下,其度分布大致在一条斜率为-1.1708的直线附近,亦即PMFG的度分布服从参数为γ=1.1708的幂律分布。

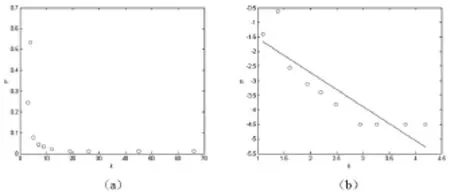
图2 复杂网络PMFG的度分布

3.3 社团结构

很多实际网络都具有社团结构,即整个复杂网络由若干个社团构成,每个社团内部的节点之间连接相对紧密,社团之间的节点之间连接相对稀疏。模块度Q是常用来衡量社团划分质量的指标[14],其上限为1,通常认为只要Q值大于0.3就说明网络存在明显的社团结构[15]。Ucinet6在划分社团结构时采用的是Girvan-Newman算法,该算法是以边介数为社团间瓶颈的社团发现算法[16]。当PMFG划分为8个社团时,模块度Q取得最大值0.427,相应的社团结构及其行业分布如图3、表2所示,其中行业分类依据为中国证券监督管理委员会2012年颁布的《上市公司行业分类指引》。

图3 复杂网络PMFG的社团结构

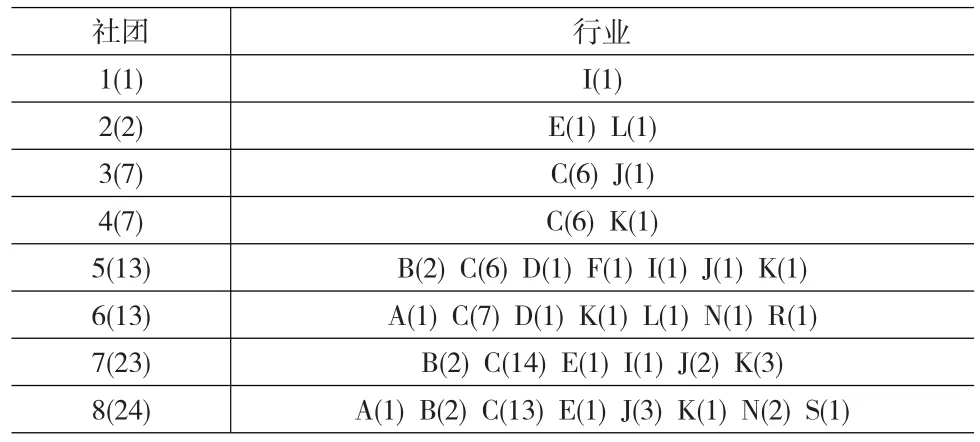
表2 复杂网络PMFG社团的行业分布

从表2中可以看到,除社团1和社团2的节点成员较少外,其余社团的行业分布呈现如下两个特点:①第二产业呈现集聚的特点,其中制造业(C)基本占了各个社团节点成员数量的一半,甚至绝大多数;②第三产业呈现分散的特点,尤其是金融业(J)和房地产业(K)几乎出现在各个社团中。以上社团结构特点说明:其一,第二产业在国民经济中仍占据着举足轻重的地位;其二,第三产业在广度、深度上都取得了长足的发展,在国民经济和社会发展中的地位日益突出;其三,相较于行业,股票收益率的波动应与产业链具有更大的相关性。股票网络的社团结构划分对于组合投资具有重要意义,投资者应当尽量将资金投资于不同社团的股票以分散投资风险,增强投资的稳定性,仅仅依赖股票的行业归属等直观信息进行决策是不可靠的。

3.4 鲁棒性与脆弱性

当复杂网络受到攻击时,网络的连通程度就会受到破坏,传输能力也会受到影响[17]。为了分析复杂网络PMFG的鲁棒性与脆弱性,考虑两种节点去除策略[18]:①蓄意攻击策略,即从去除网络中度最高的节点开始,依次去除部分度最高的节点;②随机故障策略,即完全随机地去除网络中的部分节点。f为去除的节点数占复杂网络PMFG总节点数的比例,S为最大连通子图的相对大小,L为平均路径长度,各指标的变化趋势如图4所示,其中对于随机故障策略取50次独立实验的平均值。可以看到,由于复杂网络PMFG具有无标度特征,对随机故障具有较高的鲁棒性,最大连通子图的相对大小下降得较为缓慢,平均路径长度的变化则并不显著;但是,对于蓄意攻击具有高度的脆弱性,去除网络中少量度最高的节点就可破坏网络的连通性,在去除40%左右的节点时,S就趋紧于0了。由于股市对经济的波动是异常敏感的,因此搜集关键股票节点的信息,掌握经济冲击股市的方式和范围,对维持股市的稳定、防止遭受恶意破坏、保持国家经济的稳健发展都有着十分重要的意义。

图4 复杂网络PMFG的鲁棒性与脆弱性

4 结论

复杂网络的建模方法对于非线性系统的分析提供了一种新的研究方法,但以往以线性系统中的Pearson相关系数为基础构建复杂网络的方法与非线性系统的建模初衷是不相吻合的。本文以深证股票为研究对象,以非线性系统中衡量两个变量相关关系的互信息指标为基础,构建了复杂网络PMFG。

通过对其拓扑性质进行分析,认为复杂网络PMFG具有小世界特征,说明深证股票市场的信息传递效率较高,股票的紧密程度也较高;网络中大多数的节点度数很小,但也存在少量Hub节点,具有无标度特征;网络具有明显的社团结构,呈现第二产业集聚、第三产业分散的特点,股票收益率的波动与产业链具有更大的相关性;网络对随机故障具有较高的鲁棒性,而对蓄意攻击具有高度的脆弱性。

在以往对以Pearson相关系数为基础构建的复杂网络的研究中,复杂网络同样具有明显的社团结构,但显示的是股票收益率的波动与行业具有更大的相关性[19]。本文的结论与此有所区别,该差异可能来自于以下几个原因:研究方法的差异导致结论的差异、我国股票市场的有效程度不如美国等发达国家、我国的产业结构仍处在不断调整的过程中。因此,就我国股票网络的社团结构及其内部构成还有待进一步的分析。

[1]黄登仕.金融市场的标度理论[J].管理科学学报,2000,3(2).

[2]Patton A J.Copula一Based Models for Financial Time Series[A].Andersen T G,Davis R A,KreiB J一P,et al.Handbook of Financial Time Series[M].Heidelberg:Springer,2009.

[3]马源源,庄新田,李凌轩.股市中危机传播的SIR模型及其仿真[J].管理科学学报,2013,16(7).

[4]张鼎,庄新田,卢文娟,曲红涛.基于复杂网络理论的期货指数网络的研究[J].系统管理学报,2014,23(1).

[5]张鼎,庄新田,卢文娟.我国沪深股市同配性和网络导航现象研究——基于复杂网络理论[J].技术经济,2013,32(7).

[6]黄玮强,庄新田,姚爽.中国股票关联网络拓扑性质与聚类结构分析[J].管理科学,2008,21(3).

[7]Meyer PE,Lafitte F,BontempiG.Minet:A R/Bioconductor Package for Inferring Large TranscriptionalNetworksUsingMutual Information [J].BMCBioinformatics,2008,9.

[8]Moon y I,Rajagopalan B,Lall U.Estimation ofMutual Information Using KernelDensity Estimators[J].PhysicalReview E,1995,52(3).

[9]Zeng X,Durrani TS.Estimation ofMutual Information Using Copula Density Function[J].Electronics Letters,2011,47(8).

[10]韩敏,刘晓欣.基于Copula熵的互信息估计方法[J].控制理论与应用,2013,30(7).

[11]龚伟.基于信息熵和互信息的流域水文模型不确定性分析[D].北京:清华大学硕士论文,2012.

[12]Kraskov A,Stogbauer H,Andrzejak RG,et al.Hierarchical Clustering Using Mutual Information[J].Europhysics Letters,2005,70 (2).

[13]Tumminello M,Aste T,DiM T,et al.A Tool for Filtering Information in Complex Systems[J].Proc.Natl.Acad.Sci.USA,2005,102 (30).

[14]Newman M E J,Girvan M.Finding and Evaluating Community Structure in Networks[J].PhysicalReview E,2004,69(2).

[15]Newman M E J.Detecting Community Structure in Networks[J].European Physical Journal B,2004,38(2).

[16]Girvan M,Newman M E J.Community Structure in Socialand BiologicalNetworks[J].Proc.Natl.Acad.Sci.USA,2002,99(12).

[17]KurantM,Thiran P,Hagmann P.Error and Attack Tolerance of Layered Complex Networks[J].PhysicalReview E,2007,76(2).

[18]Albert R,Jeong H,BarabásiA L.Error and Attack Tolerance ofComplex Networks[J].Nature,2000,406.

[19]Jiang X F,Chen TT,Zheng B.Structure of Local Interactions in Complex FinancialDynamics[J].Scientific Reports,2014,(4).

(责任编辑/亦民)

F830.91

A

1002-6487(2016)20-0160-04

胡振华(1962—),男,湖南邵阳人,教授,研究方向:金融计量、货币政策。覃子龙(1982—),男,湖南张家界人,博士研究生,研究方向:复杂网络、金融计量。