基于遗传分层序列法的云制造资源优化配置

汪勇,徐琼,张凌,王静

(武汉科技大学管理学院,武汉430081)

基于遗传分层序列法的云制造资源优化配置

汪勇,徐琼,张凌,王静

(武汉科技大学管理学院,武汉430081)

文章针对分层序列法和非支配排序遗传算法在求解多目标决策问题时的不足,结合遗传算法和分层序列法的优势,提出一种遗传分层序列多目标决策方法。设计遗传分层序列法的分层目标、遗传策略和原目标无量纲化处理方法。考虑运输时间因素,以制造完成时间最短和制造成本最低为目标,建立多制造任务资源分配模型,并设计一种基于时间矩阵的多制造任务完成时间计算方法。实验表明,应用遗传分层序列法进行多制造任务资源优化配置时,效果优于标准遗传算法和非支配排序遗传算法,可以满足决策者的不同决策偏好。

云制造;资源分配;多目标决策;遗传分层序列法

0 引言

随着互联网、云计算和物联网等技术的迅猛发展,云制造[1]已成为学界和业界关注的热点。云制造资源分配是一个多目标优化问题,国内外学者提出了不同的网络化制造资源分配模型。考虑交货期和成本等因素,朱金达等提出了联盟企业多目标任务分配的数学模型[2]。彭建刚等以最小化最大完工时间、机器总负荷和最大机器负荷为目标,研究柔性作业车间调度问题[3]。面向多任务制造,为使生产计划合理、高效和优化,Manupati等构建了多任务过程计划选择模型[4]和基于产品和企业重要性分级的生产计划任务分解分配模型[5]。

多目标问题通常采用指派法、分层序列法、贝叶斯矩阵[6]和智能优化方法求解。由于云制造涉及的企业和资源种类不同,任务复杂,导致资源优化配置方案巨大。面对云制造资源分配的实时性要求,本文结合分层序列法的优势,设计一种快速的多目标遗传算法,以满足决策者的不同决策偏好。

1 遗传分层序列法

1.1 目标设计

分层序列法是多目标决策的一种方法,其本质是按一个原始目标选择若干可行解,再按另一目标缩小可行解的范围,直至所有目标分析完成为止。分层序列法不适合求解具有巨型解空间的多目标决策问题。在分层序列法和遗传算法基础上,本文设计另一种多目标决策方法,即遗传分层序列法(GLM)。该方法有两个分层序列目标,第一层目标是原始目标值之和,第二层目标是原始目标的离差均值。设某多目标决策问题有n个目标,且要求所有目标最小化,则第一层目标可表示为:

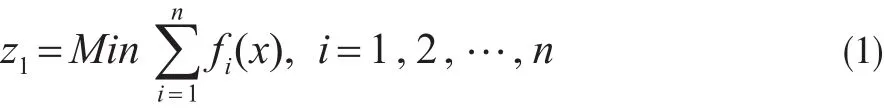
原始目标量纲不同,直接相加缺乏语义,且目标之和最小往往并非最优解。假设决策者设置的原始目标宽容值为Fi,i=1,2,…,n,采用基准法对原始目标进行无量纲化处理得:

公式(2)计算遗传分层序列法的第一层目标,同时也作为遗传算法的适应度函数。z1越小,表示该决策方案至少有一个目标较优,但目标整体性能不一定最优,需要进一步考察原始目标的离散程度。原始目标的离差均值可以区分决策方案的优劣,故采用离差均值作为遗传分层序列法的第二层目标计算方法。假设有m个可行方案,则各方案的离差均值为:

z2越小,表示决策方案的原始目标值较为均衡,目标整体性能较好。z2越大,表示该决策方案原始目标中至少存在一个较优目标。根据决策者的偏好,选择z2决策原则。

1.2 遗传策略设计

假设每代的制造资源分配方案为N个,选择、交叉和变异概率分别为ps,pc和pm。

(1)选择策略

根据公式(2),将z1升序排列,从小到大间隔选择N×ps个方案组成第t代的选择方案集Xs(t),显然,Xs(t)包含精英个体。

(2)交叉策略

随机选择N×pc个不相同的方案作为交叉个体,依次两两顺序配对,采用多点等位交叉,得到交叉个体集Xc(t)。

(3)变异策略

随机选择N×pm个不相同的方案作为变异个体,多点变异,得到变异个体集Xm(t)。则第t+1代种群X(t+1)=Xs(t)∪Xc(t)∪Xm(t)。

选择策略保证优良基因得意延续,交叉和变异策略确保种群个体多样性,避免算法陷入局部最优。

1.3 GLM算法流程

针对一组决策方案,按公式(2)计算第一层目标值并保存本代最优方案。通过遗传操作获得新的种群,重复上述步骤,直到满足终止条件为止。按公式(3)比较各代最优方案的离差均值,根据决策者偏好,选择多目标决策的最优方案。算法流程见图1。终止条件一般设定为最大进化代数。

图1 GLM算法流程

2 多制造任务资源分配模型

2.1 问题描述

多制造任务是指共享云制造平台或企业专有云制造平台接收不同产品的制造任务,且这些任务的部分工序使用相同的制造资源,每个任务的批量进行整体资源分配。设有m个处于不同地域的企业,共有n类资源,每个企业拥有的资源数量、单位加工时间和单位加工成本分别为q,PT和PC。企业间的运输时间为DT。现有k个订单需要加工,批量分别为b1,b2,…,bk,任务i的工艺路线为Ri= [ri1,ri2,…,rip(i)],ria表示任务i第a道工序,工序数值与资源编号对应。任务i的工艺路线共有p(i)道工序组成。PTia, PCia分别表示任务i第a道工序的单位加工时间和单位加工成本,DTia表示任务i从第a-1道工序运输到第a道工序的时间,WTia为任务i到达第a道工序时的等待加工时间。

若为任务i(1≤i≤k)的每道工序分配拥有相应资源的生产企业,按照工序顺序构成的企业集合就是任务i的资源分配方案Xi,Xi=[Xi1,Xi2,…,Xip(i)],则完成所有任务的资源分配方案X={X1,X2,…,Xk}。设每个任务的加工完成的时间分别为T1,T2,…,Tk,完成所有任务的加工成本为C。在满足资源数量约束和资源不冲突的条件下,寻找一个最优方案X,使得完成所有加工任务的时间T最短且加工成本C最低,见公式(4)和公式(5)。

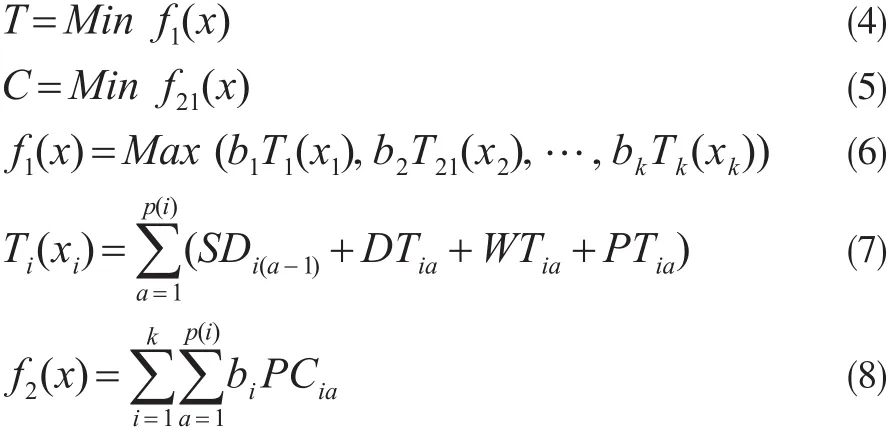
公式(5)和公式(6)表示在每组方案的最大完成时间中的最小值。Ti(Xi)表示任务i完成所有工序加工的单位时间,p(i)表示任务i的工序数。SDi(a-1)表示第a-1道工序的完成时间,也就是第a道工序的开始运输时间。令SDi0=0,即从0时刻开始计时。

2.2 约束条件

(1)设任务i第a道工序需要资源ra,ra∈R,分配的企业为Xia,1≤Xia≤m,q(Xia,ra)表示企业Xia拥有资源ra的数量,则:

(2)任务i第a道工序只能分配给一个企业加工,即在同一工序,任务不再拆分。设任务i第a道工序分配的企业为Xia,Xia⊂E,E表示可分配的企业,则:

(3)多任务一次性同时分配资源,即方案X的模为k。

(4)多个任务分配同一企业的同类资源,则按先到先加工原则进行分配。设任务i第a道工序与任务j第c道工序分配到同一企业的相同资源,若任务j先到达,且SDj(c-1)+ DTjc+PTjc≥SDi(a-1)+DTia,则任务i第a道工序的等待时间为:

(5)资源数量q和任务批量bi为正整数,N表示正整数集合。

2.3 多制造任务完成时间计算

由于每个任务的每道工序可能存在资源冲突,可以按照任务优先级、短工时优先和先到先分配的原则处理资源冲突。先到先分配是通过比较任务的运输到达时间判断是否需要等待。k个任务的工艺路线可表示为集合R=

L(i)表示任务i之前所有任务的工艺路线长度之和。若Xia表示分配给任务i第a道工序的制造企业,1≤Xia≤m, m为企业数,则资源分配方案记为X=[X11,X12,…,X1p(1);X21, X22,…,X2p(2);…;Xk1,Xk2,…,Xkp(k)]。

按照先到先分配原则,各任务制造完成时间计算步骤如下:

(1)构造进度矩阵S

设v=MaX(p(1),p(2),…,p(k)),v表示所有任务中的最大工序数。则进度矩阵为:

S的每行表示一个任务各工序的开始运输时间(SD)、到达时间(ED)、开始加工时间(SP)和加工完成时间(EP),S的每列表示各任务某个状态的时间值。

(2)初始化S

设所有任务起始运输时间相同,即第一道工序的SD= 0。不考虑等待时间,对于方案X,按照各任务工序间的运输时间DT和加工时间PT,分别计算各任务的SD,ED,SP和EP。不足最大工序数的任务,其余列设置为0。

(3)令FT=[EP11,EP12,…,EP1p(1),EP21,EP22,…,EP2p(2),…, EPk1,EPk2,…,EPkp(k)]。EPij表示各任务各工序的加工完成时间,j=1,2,…,p(i)。FT初值为0,表示该资源未被使用,非0数值表示资源已被分配,其值表示资源释放时间。

(4)更新进度矩阵

①从S的第j列开始(j初值为2),查找第j列[ED1j; ED2j;…;EDkj]中非0的最小EDij,EDij对应的是任务i的第+1道工序的到达时间,EDij=S(i,j)。任务i的第+1道工序的资源,分配的企业

②查找R中与res相同的资源,若为空,表示不存在相同的资源,则任务i的第+1道工序的后续时间SP,EP,SD和ED无须更新,因该资源已释放,但需要更新FT中任务i的第+1道工序的加工完成时间,即

③若存在与res相同的资源,则根据这些资源在R中的位置,查找X中相应位置的企业,若为空,表示分配的企业与ent不相同,则操作同步骤②。

④若这些企业与ent相同,则比较到达时间S(i,j)与相同资源相同企业的FT值,若S(i,j)≥相同资源相同企业的FT值,则操作同步骤②。

⑤若S(i,j)＜相同资源相同企业的FT最大值MFT,则任务i的第+1道工序的后续时间SP,EP,SD和 ED均加上等待时间WT,WT=MFT-S(i,j),即更新S的第i行第j+1至4X p(i)列,同时更新FT中任务i的第+1道工序的加工完成时间,FT(L(i)+

⑥重复步骤①至步骤⑤,查找第j列非0的次小EDij,直到所有任务的时间更新完毕。

(5)j=j+4,重复步骤(4),直到j=4v-2为止。

(6)确定资源分配方案X的最短完成时间,f1(X)=MaX(FT (p(1)),FT(p(2)),…,FT(p(k)))。

2.4 算法步骤

应用遗传分层序列法求解上述制造资源分配问题步骤如下:

(1)资源分配方案编码采用符号编码,Xia表示分配给任务i第a道工序的企业编号,Xia∈[1,m],编码长度L=p (1)+p(2)+…+p(k)。

(2)初始化种群X(t)={X1,X2,…,XN},t=1,2,…,MaXGen, MaXGen表示最大进化代数,N是种群内个体数,即方案数。

(3)按公式(2)计算第一层目标值,选择目标值最小的个体存入可行解集。宽容值设定为初始种群各目标的最大值。

(4)按照设计的遗传策略进行遗传操作,产生新一代种群X(t+1),重复步骤(2)至步骤(3),直到达到最大进化代数MaXGen为止。

(5)按公式(4)计算可行解集中各方案的离差均值。

(6)若决策者要求多个目标均衡,则选择具有最小离差均值的方案作为最优资源分配方案。

3 实验分析

3.1 数据准备

以湖北省8家制造企业为例(m=8),企业分布见表1所示。企业1接到两个订单的生产任务,批量分别是b1= 200件,b2=100件。任务1工艺路线为R1=[r2,r4,r3,r6,r5, r1]。任务2的工艺路线为R2=[r3,r1,r2,r5,r6]。企业间的运输时间见表2所示。

表1 企业地理分布

表2 运输时间

企业共拥有6类资源,各企业拥有的资源信息如表3所示。

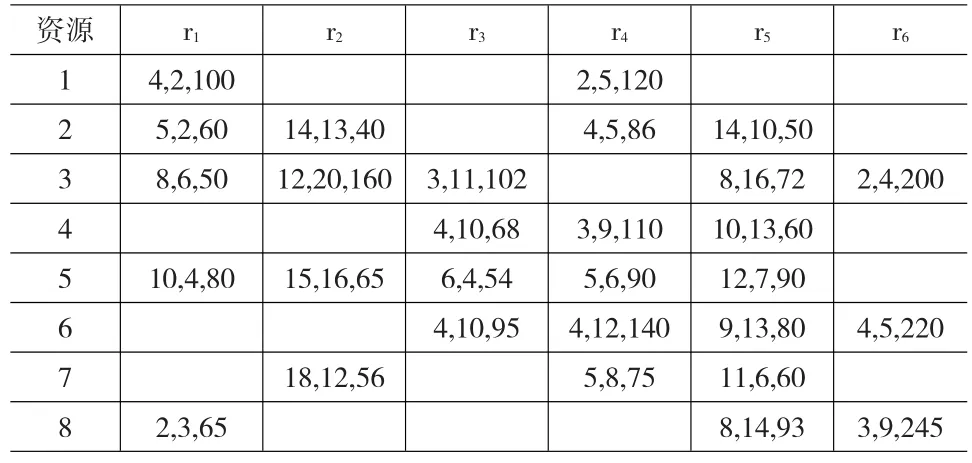
表3 企业资源

表3中的每一行代表该企业拥有的各类资源信息,单元格中第一个数据表示企业拥有某类资源的数量q,第二个数据表示单位加工时间PT(分钟/件/台),第三个数据表示单位加工成本PC(元/件)。空单元格表示企业没有该类资源。

采用GLM、NSGA-II和GA进行比较分析,GLM第二层目标采取均衡选择原则,GA采用原始目标之和作为适应度函数。三个算法的选择、交叉和变异概率分别为ps= 0.4,pc=0.4,pm=0.2,种群N=20,最大进化代数MaXGen= 1000。计算结果均为10次的平均值。

3.2 不同进化阶段的计算结果比较

三个算法在不同进化阶段的计算的制造完成时间和制造成本目标值见表4所示。

表4 不同进化阶段的目标值

表5 资源分配方案

由表4可知,三个算法分别在217代、339代和456代达到最优,分配方案见表5。GLM算法求解结果最好,NSGA-II的制造任务完成时间较GA短,但它的制造成本高于GA,目标值之和小于GA算法。尽管NSGA-II找到最优解的时间比GLM短,但在相同精度下,它的效率最低。GA收敛较早。算法的收敛特性如图2所示。

图2 不同目标的收敛曲线

观察图2可知,三个算法的制造时间(左图)、制造成本(中图)和目标之和(右图)曲线均呈下降趋势,算法均收敛。从任务完成时间来看,GLM时间最短,NSGA-II次之。从制造成本来看,NSGA-II低于GLM。综合来看, GLM性能优于NSGA-II和GA。

3.3 不同决策目标的计算结果比较

分别采用均衡决策目标、制造任务完成时间最短目标和制造成本最低目标,三个算法得到的最优资源分配方案及目标值如表6所示。

表6单元格中第一行与第二行分别表示两个任务的资源分配方案,第三行是目标值。无论决策目标如何, GLM计算的原目标之和、制造任务完成时间和制造成本均最低,优于NSGA-II和GA算法的计算结果。NSGA-II根据解的支配关系选择非劣解,其时间复杂度为N2× MaXGen,相对于GLM,NSGA-II达到相同精度的解,需要更长的计算时间。

表6 不同决策目标的资源分配方案

4 结论

计算实验表明,遗传分层序列法是一个性能更优的多目标决策方法,不仅计算速度较快,解的质量也最高,适合于多制造任务资源的优化配置。尽管遗传分层序列法在进行多目标决策时具有优势,但它的第一层采取的原目标和最优保存策略,这有可能丢失原目标较为均衡的解,如何结合解的支配关系,设计更为合理的遗传算法适应度函数值得研究。此外,云制造是一项复杂的系统工程,资源优化配置仅是其中的一项工作。关于云制造的复杂资源信息建模、可变工艺路线情形的算法编码以及不同制造模式的资源分配模型值得进一步探索。

[1]李伯虎,张霖,任磊等.再论云制造[J].计算机集成制造系统, 2011,17(3).

[2]朱金达,郑艳萍,宋海生.网络化制造环境下多目标任务分配的研究[J].河北科技大学学报,2010,31(5).

[3]彭建刚,刘明周,张铭鑫等.基于改进非支配排序的云模型进化多目标柔性作业车间调度[J].机械工程学报,2014,50(12).

[4]Manupati v K,Thakkar J J,w ong K y,etc.Near Optimal Process Plan Selection for Multiple Jobs in Networked Based Manufacturing Using Multi一objective Evolutionary Algorithms[J].Computers&IndustrialEngineering,2013,66(1).

[5]郭世伟,何霆,战德臣.网络化制造环境下的生产计划策略[J].计算机工程,2010,36(7).

[6]Chu w w,Liy G,Liu CQ,etc.AMatrix一based Bayesian Approach for Manufacturing Resource Allocation Planning in Supply Chain Management[J].International Journal of Production Research,2014, 52(11).

(责任编辑/浩天)

TP301

A

1002-6487(2016)20-0080-04

国家社会科学基金资助项目(14BTQ058);湖北省科技厅软科学研究类一般项目(2015BDF087)

汪勇(1967—),男,安徽庐江人,博士,教授,研究方向:多目标决策方法,复杂系统建模。徐琼(1989—),女,湖北红安人,硕士研究生,研究方向:进化计算,数据挖掘。