线路图设计中遵循的规律及其应用
贾锐
(陕西理工大学,陕西汉中723000)
线路图设计中遵循的规律及其应用
贾锐
(陕西理工大学,陕西汉中723000)
为保证线路图的信息传达有效,其众多设计方案必然遵循某种规律。本文利用数学定义定理的严密性来分析研究线路图的设计。以序拓扑与公交车站线路图为例进行研究,首次揭示了序拓扑与线路图的本质联系和设计线路图必须遵循的规律。然后利用这个规律指导设计,并对线路图的设计应用进行了讨论。这个规律亦可用于各种线路图的设计。
线性序;半开区间;线路图;信息传达
在信息爆炸的今天,很难避免信息超载,结果是人们很难辨别并获取真正有价值的信息,而且往往被不必要的信息甚至是错误信息所误导[1]。在设计线路图时,我们希望在设计图中保留必要的信息,屏除冗余信息,以保证方案的有效性和简洁性。本文试图用拓扑学观点阐明线路图设计中所要传达的本质信息。拓扑学主要研究图形在连续变换下保持不变的性质,并且已经在设计中有所应用。设计理论的研究者们一直尝试将拓扑学理论与设计实践相结合,如汤士东撰写的《基于拓扑形态产品造型语义的研究》[2],李滨泉等撰写的《建筑形态的拓扑同胚演化》[3]和李斌等撰写的《基于拓扑、几何关系于一体的产品模型研究》[4]等。四兵锋,陈伯阳等在《城市可变信息标识选址算法》[5]一文中,为研究城市交通对路网进行了拓扑变换得到路网拓扑结构图,使繁杂的信息变得简洁明了。这是拓扑学理论在设计中很有价值的应用。本文用线性序拓扑分析线路图的设计,揭示了线路图设计中必须遵循的规律,然后利用这个规律尝试设计两条线路的一般情况,并对三条线路中比较复杂的情况进行了设计尝试。同时我们也讨论了这些设计的应用。
1 线路图设计的拓扑学基础
为了揭示多种多样线路图设计中的不变因素,现引入拓扑学的一个领域“线性序拓扑”来研究线路图的设计。以公交车站线路图为例进行研究。首先,我们研究如何用抽象的线性序拓扑定义来描述公交线路。
1.1 车站的线性序定义
集合X在满足下列条件时称为线性序(linear order set)(拓扑空间论,定义1.8[6])。
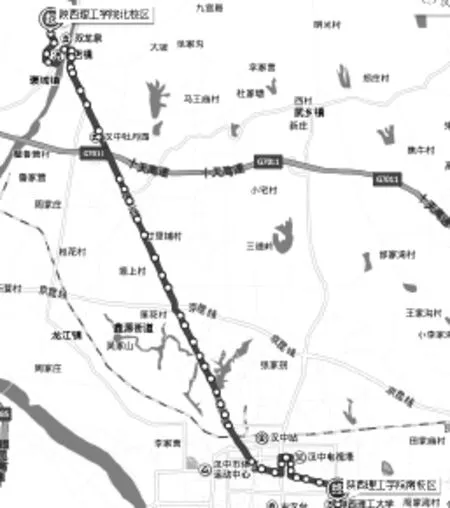
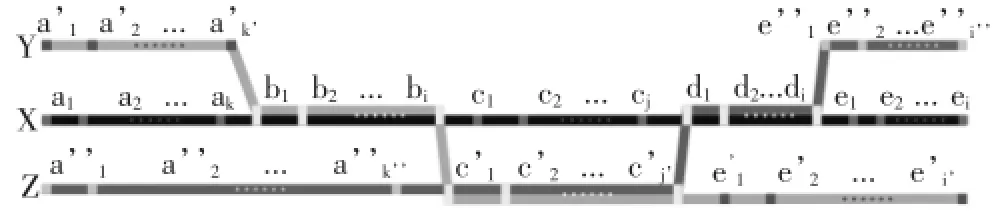
(1)任意的a,b∈X,必有a (2)任意的a,b∈X,a 注意在这里“a 我们设集合X={a,b,c,...,z}是X路公共汽车的所有车站。 条件(1)相当于X路公共汽车的任意a,b两站有a站在b站之前,或者b站在a站之前(这个可以根据实际道路情况确定)。为了方便记录为a 条件(2)相当于a 进一步再比较a站与c站,用a 如果我们把X路公共汽车中的任意两站(相当于任意的a,b∈X)都进行比较而如上所述定义出位置关系,相当于定义出X路公共汽车所有车站的位置关系如下: 也可以是c 如果返程用a1表示终点站,a26表示起点站,即a1>a2>a3>...>a24>a25>a26(iv)。则(iv)和(iii)是反对称的。因此我们只考虑(iii)。这样我们按先后顺序为X路公共汽车站点安排了一个线性序。在这里a1表示起点站,a26表示终点站。注意:数学中线性序只定义了两个元素a与b的比较。而通过以上1.1的工作,我们为任意有限个车站赋予和实际具体情况相符合的线性序。 1.2 为了研究线性序拓扑的定义与公交车站的本质联系我们引入半开区间(half-open interval)和序拓扑(order topology)[7]定义如下: 设an [an:这里方括号“[”表示乘车路段包括an站和从an到an+1,这个区间,因为这名乘客在an站已经上车至少到an+1这个站才可能下车。 am):这里圆括号“)”表示乘车路段不包括am站,因为这名乘客在am站已经下车。特别,在am=a26时,由于a26是终点站必定用方括弧“]”,就成为[an,a26]。 则可以证明CE为线性序空间X的一个拓扑,AE为线性序拓扑空间X的一个基(bases)。我们略去极为简单的纯数学化证明过程,而致力于拓扑空间与实际具体情况的联系和应用。 注意在这里,AE实际上是指一名乘客如果只乘一次车,所有可能上下车的车站和此次乘车所经过的车站。也就是一名乘客所有的可能乘车区间。例如,这名乘客如果在任意站[an上车(an CE实际上是指一名乘客想乘X路车在沿线多次上下车,所有的可能上下车车站和多次乘车经过的所有车站。 先对本文出现的重要语词定义进行明确区分。据《汉典》[8],路线是指从一地到另一地所经过的道路;线路是细小狭窄的道路及电流或运动物体所经过的路线。显然路线更贴近路本身的形态特征,更倾向于路径形象的表达;而线路从属于路线,是路线的抽象,更倾向于路径线性的表达。现为了便于研究,我们将路线定义为接近真实的地理形态,线路定义为途经站点的线性序表达。也就是说路线更强调原本路途形的特征,而线路更强调原本路途上站点的顺序特征。以上作为为本文路线和线路两词的使用依据。 现以X路公交路线为例展开分析。如下图1是在百度地图上查找到的C市X路公交路线图。由于是在地图上表达公交路线,需要尽可能的再现真实的路途形态,因此该路线是由站点所在的地理位置连接而成,基本真实的再现了该路线的地理方位特征,并详细展示了相关停靠站点的位置关系,甚至可以看到该路线穿过一条河流及若干村镇,但因为没有出现真实站点的对应名称,对不熟悉当地环境的人来说在该地图上找到目的地不是一件容易的事情。 图1 C市地图上的X路公交路线 假如一名乘客决定乘坐X路公交车并明确乘车方向后,接下来需要确定的是从哪里上车,相当于确定自己初始乘车车站的站名。在线性序拓扑空间等同于找出某个半开区间的左端点[an,至于这个左端点距始发站有多少公里等问题都不是本质特征。乘客上车后在乘车区间内对于公交车经过那些街道,几条河流,具体行驶几公里,汽车在路上什么时候该向哪个方向行驶,等等,这些在地图上被明确表示的问题都不是乘客所关心的本质问题。真正关心的本质问题是区间右端点am是什么,即这名乘客乘上车后最关心的问题是:途经多少站点后在哪一站am)下车。这些信息恰恰全部被包含在拓扑空间的半开区间[an,am)里。而另一方面,半开区间[an,am)表示乘车站[an左端点,经过an,an+1,…,am-1这n-m个车站后,在右端点am)站下车,所以半开区间[an,am)不能表示线路上的其它具体地理特征,即半开区间[an,am)包含且仅仅包含乘车站、经过车站和下车站这些信息。这就是序拓扑与线路图本质的联系。用序拓扑包含的全部信息设计公交线路图不会漏掉必要的信息,也不会包含不必要的信息。在此指导思想下就可以设计出清楚明晰的公交线路图。 按照第1,2节的讨论,我们可知公交线路符合线性序拓扑定义的要求,因此按照线性序拓扑的特征,不论拉长,缩短或弯曲公交线路图上的线段,只要不更改站点元素的顺序,该线性序拓扑性质保持不变。也就是说在设计公交线路图时,只要能保证站点顺序表达准确,乘客就能够明确自己的乘坐区间[an,am)。这就说明公交线路图的本质特征在于站点的顺序及方向。现对线性序拓扑所揭示出的线路图设计本质规律表述如下:要且只要清楚表达站点名称的顺序。即就是说,站点名称的顺序是线路图设计的不变因素,应作为设计的重点。为方便,称仅包含这些因素的线路图为拓扑线路图。据现有资料,拓扑线路图多用于长途汽车和有轨线路。 3.1 一条公交线路的拓扑线路图设计 如果所设计的只是一条公交线路,这条规律已经被设计者不自觉地广为应用,如下图2. 图2 一条公交线路的情况 3.2 两条线路的拓扑线路图的设计 现在讨论两条线路,令X={a1,...,ak,b1,...,bi,c1,...,cj,d1,...,dh,e1,...,el}表示X路公共汽车所有的车站且满足: a1<... 令Y={a’1,...,a’k’,b1,...,bi,c’1,...,c’j’,d1,...,dh,e’1,...,e’l’}表示Y路公共汽车所有车站且满足: a’1<... 则X路公共汽车有相应的基AEx和拓扑CEx,同理对Y路汽车也有基AEy和拓扑CEy.我们用X∩Y表示这两路公共汽车共有的站点。则X∩Y={b1,...,bi,d1,...,dh}。用AEx∩AEy表示这两路公共汽车所有可能的共有乘车区间。则 称之为“2交情况”,即有两段分开相交区间的情况。 (1)取[bn,dm)x∈AEx.则[bn,dm)x={bn,...,bi,c1,...,cj,d1,...,dm}。注意c1,...,cj站都不在Y路公共汽车上。则[bn,dm)x不属于AEx∩AEy.同理[bn,dm)y∈AEy.则我们有[bn,dm)y不属于AEx∩AEy. (2)一般若b1=...=bi且不存在d1,...,dm,则表示X路与Y路车只有一个共同停靠站且没有共同行驶区间。 (3)若b1=...=bi,d1=...=dm且b1≠d1,则表示X路与Y路车有两个共同停靠站且没有共同行驶区间。 (4)令B={b1,...,bi}表示Ⅰ类商品街在X路与Y路车共同停靠区间内的所有车站,D={d1,...,dh}表示Ⅱ类商品街在X路与Y路车共同停靠区间内的所有车站。有时也有p1 (5)在“2交情况”里,X路与Y路有三段不同的公交区间。它们是:Xa={a1,...,ak},Ya={a’1,...,a’k’},Xc={c1,...,cj},Yc={c’1,...,c’j’},Xe={e1,...,el}和Ye={e’1,...,e’l’}。在设计图上每一段线路图有两种设计方案:Xa线段在Ya线段的上侧或Xa线段在Ya线段的下侧。则三段共有8种设计方案。注意我们已有一条线路X路的理论基础和设计基础,把这些基础应用到两条线路来。考虑到对称因素,则仅有两种设计方案,如下图3和下图4. 图3 “2交情况”的第一种方案 图4 “2交情况”的第二种方案 3.3 “2交情况”拓扑线路图的讨论 (1)如果考虑公交站牌设计中线路图占用空间大小的问题,显然第二种方案更合适。根据我们在第1节和第2节所得到的结果,第二种方案决不意味着X路车的路线在Y路车的北侧。 (2)就“2交情况”讨论公交线路的规划设计。假设Xa,Ya,Xc,Yc,Xe,Ye为城市居民区,而Xb=Yb,Xd=Yd为商业区,如电子街或服装街。而X,Y为连接商业区和居民区的公路。我们可以根据居民区的分布和不同商品的需求程度来规划设计公交线路。如果公路X,Y的区间还有工业区,文化区等,那么我们就要根据具体客流来规划设计公交线路。根据刘剑锋在《北京轨道交通网络化客流特征分析与启示》一文中给出的资料,北京市轨道交通日客运量从2000年的119万人次增长至2011年的700万人次以上[9]。那么随着客流变化,我们有必要在一些区段增加新的线路。例如,当从a1站到c’j’站之间的客流增大时,根据需要我们可以增加Z={a1,...,ak,b1,...,bi,c’1,...,c’j’}路车。增加Z路车后,与Z路车相应的另一些区段还要调整车次以适应客流的变化。 (3)拓扑线路图也可应用于电子地图的设计。现在利用电子地图导航非常便利,当我们输入出发点和终点时,计算机程序会提供一条或几条可行的路线。图4给出的拓扑线路图可以作为电子地图设计的依据。比如从ak到e’l’站有许多不同的走法,通过图4“2交情况”方案设计,很容易设计出从ak到e’l’站的所有走法,然后计算机根据道路的不同情况(如堵车,修路等)通过分析就可以得到最佳路线。 3.4 三条线路的拓扑线路图的设计 三条或三条以上的线路图就要比二条复杂的多。据现有资料,拓扑线路图多用于长途汽车和有轨线路。所以我们仅对X,Y,Z两两相交且两交仅有一段共有区间的情形进行分析研究。 设X={a1,...,ak,b1,...,bi,c1,...,cj,d1,...,dh,e1,...,el}且满足 a1<... Y={a’1,...,a’k’,b1,...,bi,c’1,...,c’j’,e’1,...,e’l’}且满足a’1<... a’’1<...a’’k’’ 则我们有公式: AEx∩AEy={[bn,bm)|bn 根据公式(1),(2)和(3),三条公交线路两两相交拓扑线路图设计如图5所示。 图5 三条公交线路两两相交的情况 我们可以根据两条线路(1),(2),(3)的应用对图5进行讨论。 限于篇幅,本文就三条线路仅仅研究了一种普遍情况的设计。四条或更多条线路情况更没有涉及,如有需要,我们可以根据客户的实际情况和实际要求,在第1,2节中得到的基础理论指导下做出拓扑设计图。 本文首先分析了线性序拓扑和路线图的关系,揭示了线路图和线性序拓扑的本质联系。找到了设计拓扑线路图时必须遵循的规律。然后我们利用这些研究结果,尝试设计了一些公交线路图并讨论了它们的应用。 [1]张志贤.信息的可视化图像表现[J].美术与设计,2015,12(10):204-207. [2]汤士东.基于拓扑形态产品造型语义的研究[J].包装工程,2010,31(16):35-37. [3]李滨泉,李桂文.建筑形态的拓扑同胚演化[J].建筑学报,2006,21(5):51-54. [4]李斌,张再勇,黄剑等.基于拓扑、几何关系于一体的产品模型研究[J].中国机械工程,2005,16(23):35-37. [5]四兵锋,陈伯阳,蒋明清,等.城市可变信息标识选址算法[J].交通运输工程学院,2015,15(6):110-117. [6][日]儿玉之宏,永见启应著,方嘉琳译.拓扑空间论[M].科学出版社,1984:3. [7][美]凯莱著,吴从忻,吴让泉译.一般拓扑学[M].科学出版社,2010:4,38. [8]李行健.现代汉语规范词典[M].北京:外语教学与研究出版社,语文出版社. [9]刘剑锋.北京轨道交通网络化客流特征分析与启示[J].都市快轨交通,2012,25(5):27.The Rule Of Route Maps Design And The Application JIA Rui Solutions of route maps design always follow certain rules to ensure the effectiveness of the information expressions. By the preciseness of mathematical definitions and theorems,we analyze the design rules of bus route maps. Based on order topology and bus route maps,we reveal the essences of the design rules at first,use the essences to guide designs,and discuss applications of the designs. The design ideas can be applied to guide route maps designs and to reveal design rules which also could be used for various route maps designs. linear orders;half-open intervals;route maps;information expressions U121 A 1672-545X(2016)09-0213-04 2016-06-11 国家自然科学基金(11171162) 贾锐(1982-),女,陕西咸阳人,硕士,讲师,主要研究方向为设计方法学,设计符号。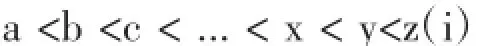
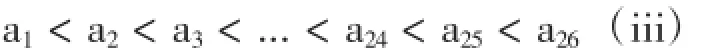
2 地图上公交路线和序拓扑的本质联系
3 公交线路图的设计

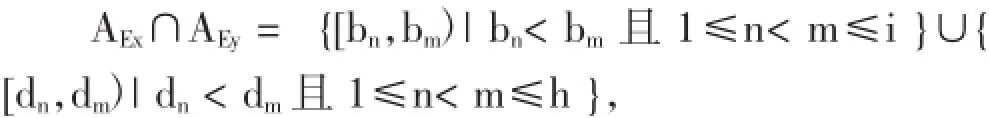



4 结束语
(Shannxi Sci-Tech University,Hanzhong Shannxi 723000,China)

