基于密度的稀疏表示及其对烟叶分级研究

马孝腊+申金媛+刘润杰+穆晓敏

摘要：稀疏表示（SRC）中字典的构建对分级的效率和准确率至关重要，提出一种基于密度的SRC字典构建方法，并利用建立好的DSRC（基于密度的SRC）对烟叶进行分级。该方法将减法聚类算法中基于密度选择中心的思想应用于稀疏算法中进行字典构建，通过确定合适的聚类半径kia、kib以及约束条件来确定字典原子，不仅可减少字典原子数目，而且选择的字典具有更好的代表性。基于该方法选择的字典对2013年（13个等级）、2014年（6个等级）和2015年（42个等级）的烟叶进行分级，试验结果表明，该方法不仅可以提高烟叶分级的准确率，而且还可以有效地提高烟叶分级速度。

关键词：减法聚类；稀疏表示；烟叶分级；字典

中图分类号： TP391.4；S126 文献标志码： A

文章编号：1002-1302（2016）09-0371-03

现阶段，在我国的烟叶收购过程中，大多是通过人工方式来对其进行分级。这种带有较大主观性的分级方式在人力、物力有限的情况下，存在较大的误差，进而影响卷烟质量。近年来，计算机和人工智能技术越来越多地被应用于农产品检测中，基于计算机视觉和红外光谱分析技术的烟叶无损分级引起越来越多的关注[1-2]。

基于计算机视觉的烟叶分级研究主要集中于识别方法和数字图像特征筛选方法的研究[1-2]。用于烟叶智能分级的方法有很多，如最近邻、径向基神经网络、支持向量机、Adaboost、粗糙集、随机森林[3]和稀疏表示[4]等，在文献[4]中简单地随机地选择每级烟叶中的2/3作为字典原子建立稀疏表示字典，这样选择的字典不仅原子数目大，影响烟叶分级时间，而且可能选择了不正确的样本作为字典，因而影响烟叶分级的准确率。合适的字典对烟叶分级的准确率和速度都有重要的影响，为此本研究提出一种基于密度的稀疏表示算法对烟叶进行分级。

减法聚类算法是Chiu于1994年在山峰聚类算法的基础上提出的，此方法根据欧氏距离准则对每个样本点计算其密度值（山峰值），选择其中密度最大的点作为聚类中心[5]。然后对剩余样本的密度进行更新，重复选择密度值最大的样本点直到到达设定的条件为止。本研究将减法聚类算法中基于密度的聚类中心的选择思想应用于稀疏表示的字典原子构建中，提出一种基于密度的稀疏表示方法[6]。通过确定每类中合适的聚类半径kia、kib以及约束条件确定字典原子数目和选择字典原子，然后通过求解L1范数最小化问题和最小残差项对烟叶进行分级，结果表明本方法可以在保证一定识别率的前提下有效提高烟叶分级的速度。

1 基于密度的稀疏表示（DSRC）

1.1 稀疏表示（SRC）原理[7]

稀疏表示算法首先通过训练样本构建字典，然后利用测试样本对字典的投影进行模式识别。常见的字典构建原理如下，假设模式分属于C类，第i类的训练样本集为：

kib的取值一般大于kia是为了避免距离太近的聚类中心；根据更新后的密度选择出Di2，以此类推，可选择出所有的中心Di3，Di4，…，DiLi。

1.3 改进SRC算法

稀疏表示中影响输入模式分类的主要因素有2个，一个是字典原子的构成，另一个是最佳稀疏矩阵X的求解方法。其中字典原子的数目会极大地影响稀疏表示的分级速度，进而影响到该方法的实时使用性能；而字典原子的特性则不仅仅影响字典原子的数目而且会直接影响稀疏表示分级的正确性。一个好的字典应该不仅具有良好的代表性、遍历性，而且数目应该尽可能地少。具有非常好的代表性的原子，即以较少的原子实现样本的遍历性。没有经过分析选择的训练样本，其代表性不一定很好。因此本研究提出利用基于密度的减法聚类算法进行字典的原子选择。

根据公式（4）计算第i类样本点的密度值，选择密度最大的样本作为第1个原子Di1；然后利用公式（5）进行样本点的密度值更新，选择具有密度最大的样本作为第2个原子Di2，依此类推可选择出所需要的所有原子Di3，Di4，……，DiLi。

邻域半径值kia、kib的选择非常关键，极大地影响字典的构成；传统中邻域半径值为固定值，不能随着原始数据的特性进行调整变化，具有一定的局限性。本研究中根据公式（7）来确定第i类邻域半径kia，其公式如下：

最后利用公式（2），基于L1范数通过字典D求解系数矩阵X，并根据公式（3）求解最小残差值对输入样本进行分类。

2 实际烟叶分级结果及分析

2.1 试验对象和预处理

试验对象为河南省烟草公司平顶山市烟草公司提供的2013年（13个等级的烟叶）、2014年（6个等级，每个等级的烟叶来自5个不同的县区）和2015年（42个等级的烟叶）的烟叶，其中27组主组15组副组。烟叶分级的标准为郑州市烟草公司提供的烟叶评定准则。本研究中采集的烟叶图片是用CCD摄像机（型号为TK-C1481BEC）在暗箱中拍摄所得（图1）。

为了减少在采集数据过程中热噪声、背景噪声的影响，对图像进行中值滤波进行去噪。

基于图像选择39个特征X={xj}对烟叶进行自动分级，xj表示第j个特征的值，特征顺序j分别对应为长，宽，长宽比，面积，周长，破损率，圆形度，矩形度，R、G、B、H、S、I的均值和方差等，能量，惯性，相关性，熵（烟叶的4个纹理特征），脉络长，脉络宽，脉络比，脉络的R、G、B、H、S、I的均值和方差等。为了提高分级率以及减少建立分级模型所需的时间，对特征数据按照公式（9）进行归一化：

2.2 结果分析

试验时选择其中的1/3为训练样本，2/3为测试样本。根据公式（6）、公式（7）对聚类半径kia、kib进行确定，在求解聚类半径的时候，主要确定合适的参数值T1、T2。

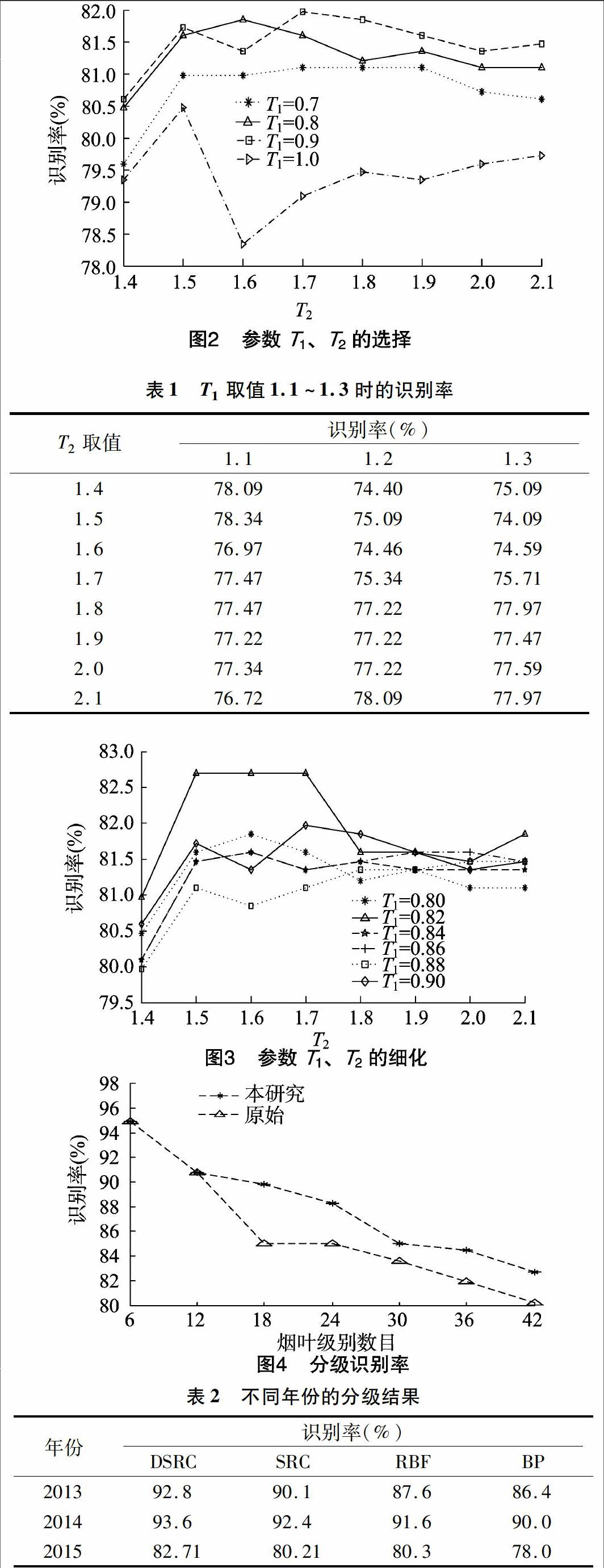
图2为采用网格遍历法对参数T1、T2进行筛选，横轴为参数T2的取值范围，纵轴为对应的识别率，从图2中可以发现在T1为0.8和0.9时的识别率相对其他参数值具有较好的识别效果。表1为T1取值1.1、1.2、1.3时的识别率，结合图2、表1可以进一步看出T1在0.8到0.9之间相比其他值具有更好的识别效果。

从图2中可知，在T1为0.8和0.9时，两者有一定的交叉重叠部分，不能确定T1的具体取值，故进一步对范围为0.8～0.9的T1进行研究，以寻找最佳的参数选择，结果如图3所示。横轴为参数T2的取值，纵轴为对应的识别率，从中可以看到在T1为0.82的时候识别率达到最大值，在确定T1后，根据公式（6）进行参数T2的选择，从图3中可以看到在T1为 0.82时，T2在1.5、1.6、1.7处具有相同的识别率（最大识别率）。

求解系数矩阵X的时候，字典中原子个数的数目直接影响烟叶的分级速度，为了提高烟叶分级速度本研究利用DSRC对字典样本进行筛选，选择一些具有较好代表性和遍历性的字典原子，经筛选后的样本数（365）比原始字典数 （588）约减少一半。因此，在识别率形同的前提下，选择具有较少原子个数的字典，在T2的取值为1.7时（365个字典原子），相比其他具有较少的原子个数，因此选择T2为1.7。

基于确定的参数T1、T2即聚类半径kia、kib选择构成字典的原子，最后对对测试烟叶样本进行分级；图4所示为SRC和本研究中提出的DSRC随烟叶类别数目变化的分级结果。图中星形标志为本研究提出基于密度的稀疏表示的分级结果，三角形标志为原始稀疏方法的分级结果，横坐标为烟叶级别数目，纵坐标为其对应的识别率。显然DSRC比SRC的识别率有明显的提高，在烟叶级别数目为18时，两者识别率相差5百分点。

对于所选择的训练样本不可避免地存在错误分类的样本。由于错分类的样本具有更小的密度，所以基于密度选择的原子可去除一些可能错误分类的训练样本，约束条件又保证了它们和原始字典具有基本相同的遍历性，但比原始原子具有更好的代表性。因此基于DSRC对烟叶分级可提高烟叶分级的识别率；同时由于原子数目的减少，DSRC的分级速度得到了提高。

对2013年13个等级的烟叶、2014年6个等级的烟叶、2015年42个等级的烟叶样本分别利用DSRC、SRC、BP、RBF神经网络烟叶分级模型进行分析，识别率见表2。可以看到针对不同年份，不同级别数目的烟叶，本研究提出的基于密度稀疏表示的分级效果均优于传统的SRC、BP、RBF等算法，可见此方法具有一定的实用性。

4 结论

本研究提出基于密度的稀疏表示对烟叶进行分级，通过设定合适的邻域半径kia、kib以及约束条件来确定所寻找字典。在确定字典原子后对烟叶样本进行分级，烟叶分级正确率达到94.9%。同时，本研究提出的基于密度的稀疏表示提高了烟叶的分级速度。对2013年、2014年、2015年的烟叶进行测试，均有较好的分级效果，说明本研究的方法对于不同年份的烟叶具有一定的实用性。

参考文献：

[1]赵海东，申金媛，刘润杰，等. 基于聚类的烟叶近红外光谱有效特征的筛选方法[J]. 红外技术，2013，35（10）：659-664.

[2]申振宇，申金媛，刘剑君，等. 基于神经网络的特征分析在烟叶分级中的应用[J]. 计算机与数字工程，2012（7）：122-124.

[3]秦玉华，宫会丽，宋 楠，等. 改进随机森林的波长选择用于烟叶近红外稳健校正模型的建立[J]. 烟草化学，2014（6）：64-68.

[4]向金海，杨 申，樊 恒，等. 基于稀疏表示的烤烟烟叶品质分级研究[J]. 农业机械学报，2013，44（11）：287-292.

[5]Chiu S L. Fuzzy model identification based on cluster estimation[J]. Journal of Intelligent & Fuzzy Systems，1994，2（3）：267-278.

[6]张 亮，李敏强. 半监督聚类中基于密度的约束扩展方法[J]. 计算机工程，2008，34（10）：13-15.

[7]Wright J，Yang A Y，Ganesh A，et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，31（2）：210-227.