基于时间序列的内河航道有效净宽研究
王梦紫 王艳锋
(武汉交通职业学院,湖北 武汉 430065)
基于时间序列的内河航道有效净宽研究
王梦紫 王艳锋
(武汉交通职业学院,湖北 武汉 430065)
为了研究内河航道不同水位期的有效宽度,运用时间序列分析模型对桥区水域水位随时间的变化规律进行回归分析,并结合桥区水下地形的特征向量,计算出内河航道的有效净宽。文章以武汉航段某一断面为例验证了计算模型的可行性。
内河航道; 水位; 水下地形;时间序列
随着沿江建筑物的日益增多,船舶流量和通航密度越来越多,使长江航道变得越来越拥挤,通航环境日趋复杂。同时,长江船舶大型化和标准化的发展,对长江航道的通航要求也越来越高。水位的季节性变化和水下地形条件是航道通航尺度的重要影响因素。在1936年,斯莱德提出了用对数正态曲线来确定水文物理性质[1]。邬晓光、刘来君等人运用时间序列分析方法,给出了桥梁水域水位的季节性预报模型[2-3]。García-Díaz J C运用时间序列模型揭示水文变量的动态变化规律[4]。本文运用时间序列分析方法和长江航道水下地形回归方法来建立动态模型,计算出不同水位期的航道有效宽度。
1 航道有效净宽建模
1.1 时间序列
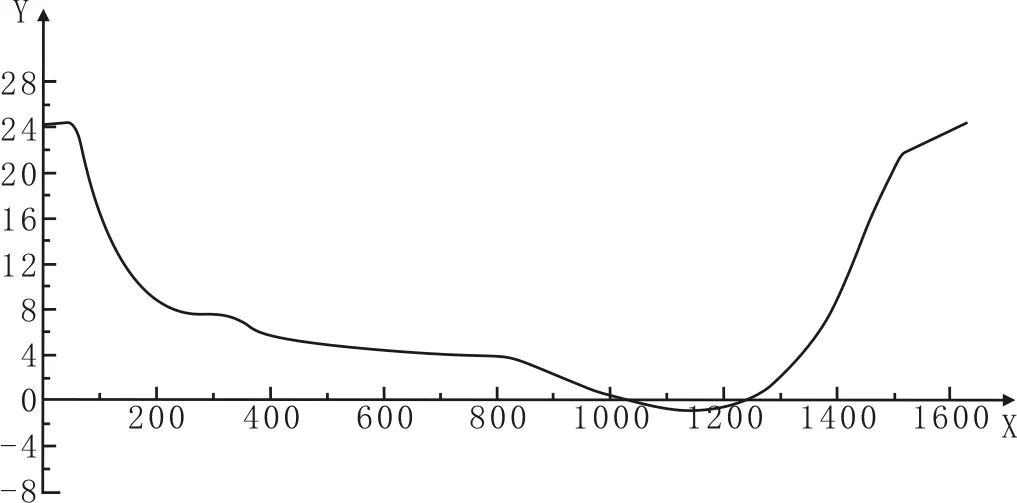
在科学研究和生产过程中,对某一个或者某一组变量x(t)进行观察和测量,并将在这一系列时刻t1,t2,…,tn(t为自变量,且t1 时间序列分析模型是根据系统观测所得到的时间序列数据,通过曲线拟合和参数估计来建立数学模型的理论和方法,它一般采用曲线拟合和参数估计法(如非线性回归法)进行。时间序列建模的基本步骤[5]:(1)取得被观测系统时间序列内的动态数据,可采用观测、统计、调查、抽样等方法;(2)依据动态数据进行相关分析,并求自相关函数;(3)通过适合的随机模型,进行曲线拟合。 时间序列分析模型主要有:趋势模型、季节模型、ARMA模型和滑动平均模型等序列分析模型。 (1) 由于河道水下地形具有不规则性,在同一水位期下,河道内的每一点水深也均不相同,总体呈现河道中间深、两边浅的趋势,水下地形的特点也制约着内河航道的有效通航净宽。 为进一步研究内河航道的有效净宽,需要对内河航道水下地形的断面变化规律进行回归分析,并建立水下地形断面方程。 建立方程方法如下:(1)采集水下地形坐标值。根据内河断面水下地形图,建立水下地形坐标系,并采集地形坐标值(X,Y)。(2)水下地形方程回归。根据水下断面图形,内河水下断面图形多呈现分段式二次抛物线形式。因此,可建立方程组: (2) 1.3 动态方程求解 根据上述计算模型,为求得内河航道某一断面的有效通航净宽,需将水位回归方程和水下地形回归方程建立在同一坐标系下,并求取在该坐标系下的不同水位期下的坐标值,即为船舶可航水域的宽度。 2.1 水位回归分析 据2014年长江武汉段相关月份水位统计资料分析可知,水位随时间的变化属于二次趋势,因此,在对水位随时间的变化分析中,采用三次指数平滑模型进行回归分析(见表1)。 据上述拟合数据得到相关参数值:a= 14.4825,b= 0.7382,c= -0.0505,均方误差=1.3385。因此,拟合后水位随时间序列的递推关系函数为: F(t)=14.4825+0.7382t-0.0505t2 (3) 其中t为时间序列。 表1 水位拟合结果 2.2 水下地形方程回归 根据武汉沌口某断面水下地形图(见图1),在AutoCAD中直接导出水下地形坐标值,由于导出的坐标值为在该CAD图形下的坐标,因此,需要将该坐标值转换为相对于0点坐标值(见表2)。 图1 桥位处断面水下地形图 序号距离X(m)地形Y1(吴淞高程m)序号距离X(m)地形Y1(吴淞高程m)120.0024.5741321240.008.02615240.0024.4859722260.007.87534351.1524.4683923280.007.716435462.1523.6068524300.007.558405570.0021.9486425320.007.400315680.0019.5724526340.007.23877790.0018.0931427360.006.8665858100.0016.6926128374.436.530059110.0015.4553829390.006.1738210120.0014.454130410.005.9486411130.0013.4099231440.005.6298312140.0012.3708632460.005.4162213147.8011.617933490.005.13855514160.0010.6787934510.005.0156515170.0010.1255235537.114.84914516180.009.7007736570.004.64317517192.169.24091537600.584.45013518210.008.5771338630.004.2778619222.308.19187539660.004.21928520230.008.10049540690.004.20877 运用matlab对上述地形坐标进行分段拟合,分段坐标点为(800,4.12971)。 拟合后计算结果: (1)当20≤x≤800时,计算可得: y=0.00006785x2-0.075305x+23.973(见图2),误差平方和=1.787289e+02 图2 水下地形拟合图 (2)当800≤x≤1635.11时,计算可得: y=0.00009169x2-0.20265x+106.97(见图3),误差平方和=1.200036e+02 图3 水下地形拟合图 通过第(1)、(2)步可以得到,桥位横断面水下地形分段函数: (4) 2.3 动态模型计算分析 根据方程(3)和(4)联立计算可得,武汉沌口河段某断面2014年随水位变化的可航水域宽度见表3和图4。 表3 不同水位期通航净宽 图4 不同水位期通航净宽 综合上述计算可知: (1)根据上述对长江武汉段水位的拟合计算结果可知,在5月和10月,长江水位由低水位升至高水位和由高水位降至低水位,水位变化较大时,出现两个较大的残差值。可以根据每天实际观测值,采用时间序列分析法,可有效降低误差。 (2)根据上述对沌口桥区水下地形图拟合计算可知,由于水下地形的不规则性,以(800,4.12971)为分段坐标点,进行二段式拟合,①段的拟合误差要大于②段的拟合误差,说明在①段水下地形更加不规则,可采用多段二次拟合,以降低误差;②段二次拟合误差较小,效果较好。 (3)水位在每变化0.5m的过程中,可航水域的通航净宽变化幅度不大。但是,水位由23m降至12.5m时,可航水域宽度减少119m,整体变化幅度较大,对习惯沿江边航行的船舶影响较大。 水位的季节性变化和水下地形特性直接影响内河航道的通航尺度,运用时间序列分析模型中的三次指数平滑预测模型能够很好地分析预测内河水位的变化规律,并结合水下地形回归模型,建立动态内河航道可航水域净宽计算模型,能够有效计算出不同水位期河道断面的通航净宽,为进一步研究整个航道的有效通航净宽奠定了基础。 [1]Slade J J. An asymmetric probability function[J]. Transactions of the American Society of Civil Engineers, 1936, 101(1): 35-61. [2]邬晓光,刘来君.应用AR(P)模型预报桥梁施工水位[J].西安公路交通大学学报,1996,16(2):53-55. [3]邬晓光.桥梁施工水位预报模型的应用研究[J].桥梁建设,1996,21(3):55-57. [4]García-Díaz J C. Monitoring and forecasting nitrate concentration in the groundwater using statistical process control and time series analysis: a case study[J]. Stochastic Environmental Research and Risk Assessment, 2011, 25(3): 331-339. [5]杨一鸣.时间序列分类问题的算法比较[J].计算机学报,2007, 22(4):194-198. [6]李深洛.基于特征的时间序列聚类[D].桂林:广西师范大学,2014. [7]郭龙.时间序列数据的周期性研究[D].成都:电子科技大学,2013. [8]注册土木工程师执业资格考试港口与航道工程规范汇编 (上、下册) [M].北京:人民交通出版社,2003. [9]袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,1997. [10]王多银.长江上跨江建筑物的布设原则探讨[J].水运工程,2001, 21(3):89-95. 2016-07-07 王梦紫(1982-),女,河南洛阳人,武汉交通职业学院船员培训中心教师,主要从事海事教育教学研究。王艳锋(1982-),男,河南驻马店人,武汉交通职业学院船舶与航运学院教师,主要从事交通信息工程及控制研究。 10.3969/j.issn.1672-9846.2016.03.018 U442 A 1672-9846(2016)03-0073-04
2 模型应用






3 结论

