基于偏序任务的社会网络合作算法研究
刘 勇 韩 雪 李金宝 任倩倩 王 楠
(黑龙江大学计算机科学技术学院 哈尔滨 150080)(黑龙江省数据库与并行计算重点实验室(黑龙江大学) 哈尔滨 150080)(acliuyong@sina.com)
基于偏序任务的社会网络合作算法研究
刘 勇 韩 雪 李金宝 任倩倩 王 楠
(黑龙江大学计算机科学技术学院 哈尔滨 150080)(黑龙江省数据库与并行计算重点实验室(黑龙江大学) 哈尔滨 150080)(acliuyong@sina.com)
针对不同任务之间通常存在偏序关系这种实际情况,提出了基于偏序任务的社会网络合作问题(collaboration problem in social networks based on tasks with partial ordering relations, CSN-TPR).该问题研究如何从社会网络中选择合适的团队来合作完成具有偏序关系的任务集,使得由通信代价、时间代价和预算代价构成的总体代价性能最优.首先证明了CSN-TPR是NP-hard问题,然后利用爬山法、分支限界策略和动态规划方法提出了近似算法HillClimbingTF_BBS.HillClimbingTF_BBS算法不仅输出有效的团队,而且能给出团队成员的具体任务分配以及每项任务的开始时间. 真实数据上的实验结果表明: HillClimbingTF_BBS算法能有效并高效求解CSN-TPR.
社会网络;合作;偏序关系;爬山法;分支限界
随着社会的发展,项目的规模越来越大,社会成员间的合作愈显重要.传统的合作问题[1]研究给定项目P(P中包含若干个任务),候选人集合S以及S中每个人所会的任务集合,选择一个能完成项目P的团队,使得某个目标最优(例如完成项目时间最短或者项目花费最小).但是,这种方法忽略了团队内部个体间的合作程度,若团队内个体间互不熟悉或有矛盾,那么所选择的团队未必是一个最佳团队.
近年来,由于大规模社交网站(如Facebook、Twitter、人人网等)变得非常流行,基于社会网络的合作问题逐渐成为了数据挖掘领域的热点研究内容[2-5].基于社会网络的合作问题定义如下:给定社会网络G=(V,E),V中每个个体所会的任务集,以及由若干个任务构成的项目P,要求从V中选择一个团队T.在完成项目P的前提下,使团队T中成员间的通信代价尽可能小.通信代价可以使用最小生成树、Steiner树、密度、直径等多个标准度量[6-7].针对该问题,已经提出了多个问题变体和多种解决方法.
然而,已有研究工作在选择团队时只考虑完成项目中的所有任务,并没有考虑任务间可能具有先后顺序,某些任务只有在前序任务完成后才能开始.例如:在建楼过程中,如图1所示,首先要打地基,才能开始后续工作,楼主体结构建成后才能安装门窗和管道.没有先后顺序要求的工作又可以并行进行以提升整个工程的进度,如安装门窗和管道可以同时实施.这种任务间具有偏序关系的项目在实际应用中普遍存在.对于这样的项目,在构建团队时,不仅要完成所有任务,还要根据任务间的偏序关系给出团队成员的具体任务分配,使得整个项目的完成时间最短.

Fig. 1 An example for tasks with partial relations.图1 偏序任务示例
除了整个项目的完成时间,团队成员间的合作程度、项目的成本也是影响整个项目的重要因素,是管理者需要考虑的重要问题.因此,为了有效完成项目,最佳的团队必须综合考虑团队的时间代价、通信代价和预算代价3方面因素,使得总体代价最优.每部分代价在总体代价中所占的比重可以根据实际项目的需要由管理者自己选择.本文主要研究如何从社交网中选择合适的团队来合作完成带有偏序关系的任务集(项目),使得总体代价最优,其主要贡献有3点:
1) 提出了基于偏序任务的社会网络合作问题(collaboration problem in social networks based on tasks with partial ordering relations, CSN-TPR),并证明了该问题是NP-hard问题.
2) 利用爬山法、分支限界策略及动态规划方法提出了一个求解CSN-TPR问题的高效算法HillClimbingTF_BBS.该算法不仅输出有效的团队,而且给出团队成员的具体任务分配以及每项任务的开始时间.
3) 真实数据上的实验结果表明:HillClimbingTF_BBS算法能有效并高效求解CSN-TPR问题,此外,还通过实验给出了HillClimbingTF_BBS算法的联机近似比.
1 相关工作
社会个体如何合作高效完成任务一直是学术界的热点研究内容,因为其具有极大的社会需求和广泛的应用前景.例如:Meetup和Google都已经开发了活动合作功能,用于安排活动时间和活动参与者.
自2004年团队构建概念提出后[1],合作研究迅速成为了一个热门的研究领域,已经提出很多成熟高效的算法.大部分研究工作仅以团队完成既定任务为目标,没有考虑社会成员间的社会关系和以往的合作程度[8].近些年来的研究工作在原有合作问题的基础上进行了扩展,在完成任务的前提下尽可能降低成员间的通信代价.Lappas等人[2]首次提出了基于社会网络的合作问题,根据社会成员间以往的合作程度,并利用最小生成树、Steiner树、直径等标准度量通信代价[6-7],研究如何构建通信代价最小的团队.Datta等人[3]对社会网络合作问题加入任务负载平衡的限制.Rangapuram等人[4]和Gajewar等人[9]基于稠密子图定义通信代价,研究了社会网络合作问题.Yang等人[10]在构建团队时除了优化通信代价,也把完成任务的时间作为一个优化目标.Li等人[11]对任务给出了限制条件,规定每个任务所需的人员数,运用划分的方法求解社会网络合作问题.Kargar等人[5]综合考虑通信代价和成员报酬,提出了一个双目标的组合优化.Farhadi等人[12]和Sozio等人[13]利用社团划分方法来求解社会网络合作问题,在划分后的社团上构建团队不仅提高了挖掘效率,同时保证了结果的准确性.Anagnostopoulos等人[14]在大规模社会网络上进行社团划分,使得团队构建问题可应用于大规模网络.Sun等人[15]最近提出了社会网络上支持任务分组的团队构建问题并给出了有效的算法.
然而,已有研究工作并没有考虑完成任务先后顺序的限制,本文将针对带有偏序关系的任务集,定义社会网络合作问题,并提出有效算法求解该问题.
2 预备知识
本节描述文中所用的符号定义以及本文算法所用的2个树搜索策略.
2.1 符号定义
G(V,E)表示无向加权图,其中V为个体集,E为边集.d(i,i′)表示在图G中个体i到i′的最短距离.

P(T,R)表示项目(有向无环图),T⊆A表示项目中的任务集,R表示任务之间的偏序关系.k表示项目P中的任务数,即|T|=k.Cc(V′)表示团队V′的通信代价,即V′中个体构成最小生成树边上的权值和.Ct(V′)表示团队V′的时间代价,即完成项目所需最长时间.Cb(V′)表示团队V′的预算代价,即每个个体完成相应任务所需薪资总和.
2.2 爬山法与分支限界策略
本文中将采用爬山法解决带有任务偏序关系的社会网络合作问题.爬山法是一种深度优先树搜索算法.初始化时,构造由根节点组成的单元素栈S.在搜索过程中,判断栈顶元素p是否为目标节点,如果是,则返回目标节点搜索结束;否则弹出栈顶元素p,将p的子节点按照其启发测度由大到小(或由小到大)的顺序压入栈S,继续搜索过程.显然,在深度优先树搜索过程中,爬山法使用贪心方法确定搜索的方向,是优化的深度优先搜索策略.
本文将采用分支限界法缩小搜索空间,提高算法效率.分支限界法常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间.每一个活节点只有一次机会成为扩展节点,活节点一旦成为扩展节点,就一次性产生其所有孩子节点.在这些孩子节点中,导致不可行解或导致非最优解的孩子节点被舍弃,其余孩子节点被加入活节点表中.此后,从活节点表中取下一节点成为当前扩展节点,并重复上述节点扩展过程.这个过程一直持续到找到所需的解或活节点表为空时为止.
3 问题定义
在完成具有偏序关系的任务集而构建团队的前提下,比较合理并且实际的目标是找到的团队不仅通信代价小,而且所花费时间和预算都尽可能小.
为了找到低通信代价、低预算、高效率的合作团队,本文给出了基于偏序任务的社会网络合作问题(CSN-TPR),定义如下:
定义1. 给定社会网络G(V,E),任务域A,每个个体所会的任务集Task(V)={X1,X2,…,Xn}以及项目P(T,R),目标是找到一个团队V′⊆V和对该团队V′的具体任务分配,使得3个条件成立:

2)V′中个体完成任务的顺序应满足项目P(T,R)中要求的偏序关系R;
3) 总代价αCc(V′)+βCt(V′)+(1-α-β)Cb(V′)最小.
在上面的问题定义中,所找团队V′⊆V要满足3个条件:1)V′中所有个体被分配的任务集合可以覆盖项目P(T,R)中的任务集T.2)对T中任意任务Ti和Tj,如果在偏序关系R中Ti在Tj之前,那么Ti的完成时间应早于Tj的开始时间.注意:本文算法不仅找到所需团队,而且可以确定任务对团队成员的具体分配以及每个任务的开始和完成时间.3)本文综合考虑团队的通信代价Cc(V′)、时间代价Ct(V′)和预算代价Cb(V′),使得总代价尽可能小.其中,Cc(V′)可用最小生成树或直径等标准衡量[6-7],Ct(V′)是项目最后的完成时间,Cb(V′)是团队成员完成任务的薪资总和.α,β是平衡各部分代价的参数,根据具体的项目由管理者来确定.由于不同代价的度量范围不同,本文将社会图中权值统一为1~10范围内的数,个体完成任务的时间和所需薪资都统一为1~10范围内的数,这样可以用平衡参数计算总代价.
图2给出了一个具体的例子,社会网络G(V,E)如图2(a)中所示,要完成的项目P(T,R)如图2(b)中所示.其中,任务集合T={j1,j2,j3,j4},偏序关系R={〈j1,j3〉,〈j1,j4〉,〈j2,j4〉}.每个个体所会任务集如下:X1={(j1,4,3),(j2,2,3),(j3,5,1)},X2={(j3,2,2),(j4,1,5)},X3={(j1,4,2),(j2,3,3)},X4={(j3,3,2)},X5={(j4,2,2)},平衡参数α=0.3,β=0.4.
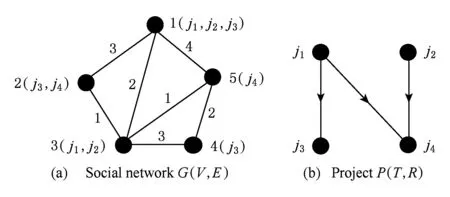
Fig. 2 The input for CSN-TPR.图2 CSN-TPR问题的输入
表1对上面的例子给出了2个候选团队,每个任务的具体分配以及任务开始和完成时间.在团队Team1中,任务j1由个体3来完成,薪资为4;任务j2由个体1来完成,薪资为2;任务j3由个体2来完成,薪资为2;任务j4由个体5来完成,薪资为2,所以预算代价Cb(V′)=4+2+2+2=10.个体3,1,2,5在社会网络(如图2(a)所示)中构成的最小生成树权为1+1+2=4,所以通信代价Cc(V′)=4.整个项目的最后结束时间是5,所以Ct(V′)=5.因此总代价为0.3×4+0.4×5+(1-0.3-0.4)×10=6.2.用类似的方法可计算团队Team2的总代价为8.3.注意:在任务分配时,多个任务可以分配给同一个个体,如Team2中任务j1和j2都分配给了个体1.这时任务j1和j2不能像Team1那样同时被执行,必须有先后顺序.在计算个体1,4,2构成的最小生成树时,尽管个体4和个体1,个体4和个体2不直接相连,但可以计算个体4和个体1的最短路径d(4,1)=5,个体4和个体2的最短路径d(4,2)=4.个体1,4,2构成的最小生成树的权为d(4,2)+d(1,2)=7.因此,Team2中的通信代价为7.

Table 1 Two Selected Teams for the Problem Shown in the Fig.2
定理1. 基于偏序任务的社会网络合作问题CSN-TPR是NP-hard问题.
证明. 如果项目中的各个任务独立,没有偏序关系,同时忽略时间代价和预算代价,只考虑通信代价(通过设置平衡参数α=1,β=0,总代价就是通信代价),那么本文所提出的问题CSN-TPR等价于Lappas等人在文献[2]中提出的原始社会网络合作问题Mst-Tf.也就是说,对Mst-Tf问题的任何一个实例,通过取α=1,β=0,就可以在多项式时间内变换成CSN-TPR问题的一个实例.因此,Mst-Tf问题可以在多项式时间内规约到CSN-TPR问题.因为Mst-Tf问题是NP-hard[2],所以CSN-TPR问题也是NP-hard.
证毕.
4 算 法
针对CSN-TPR问题,本文采用爬山法进行任务树搜索,利用分支限界策略进行剪支,提出了HillClimbingTF_BBS算法.由于在CSN-TPR问题中,任务集具有严格的偏序关系,所以时间代价的计算不能单纯地进行串行累加计算,本文应用动态规划方法来计算时间代价.
4.1 HillClimbingTF_BBS算法
根据任务间的偏序关系,可建立一棵搜索树.例如:根据图2(b)的偏序关系可建立搜索树如图3所示.利用爬山法进行树结构搜索,每步分支都选择当前所有可扩展分支中使得总代价最小的节点去扩展.设当前构建的部分团队为V′,则每步分支都应选择使总代价C(V′∪i)=αCc(V′∪i)+βCt(V′∪i)+(1-α-β)Cb(V′∪i)最小的节点i去扩展.
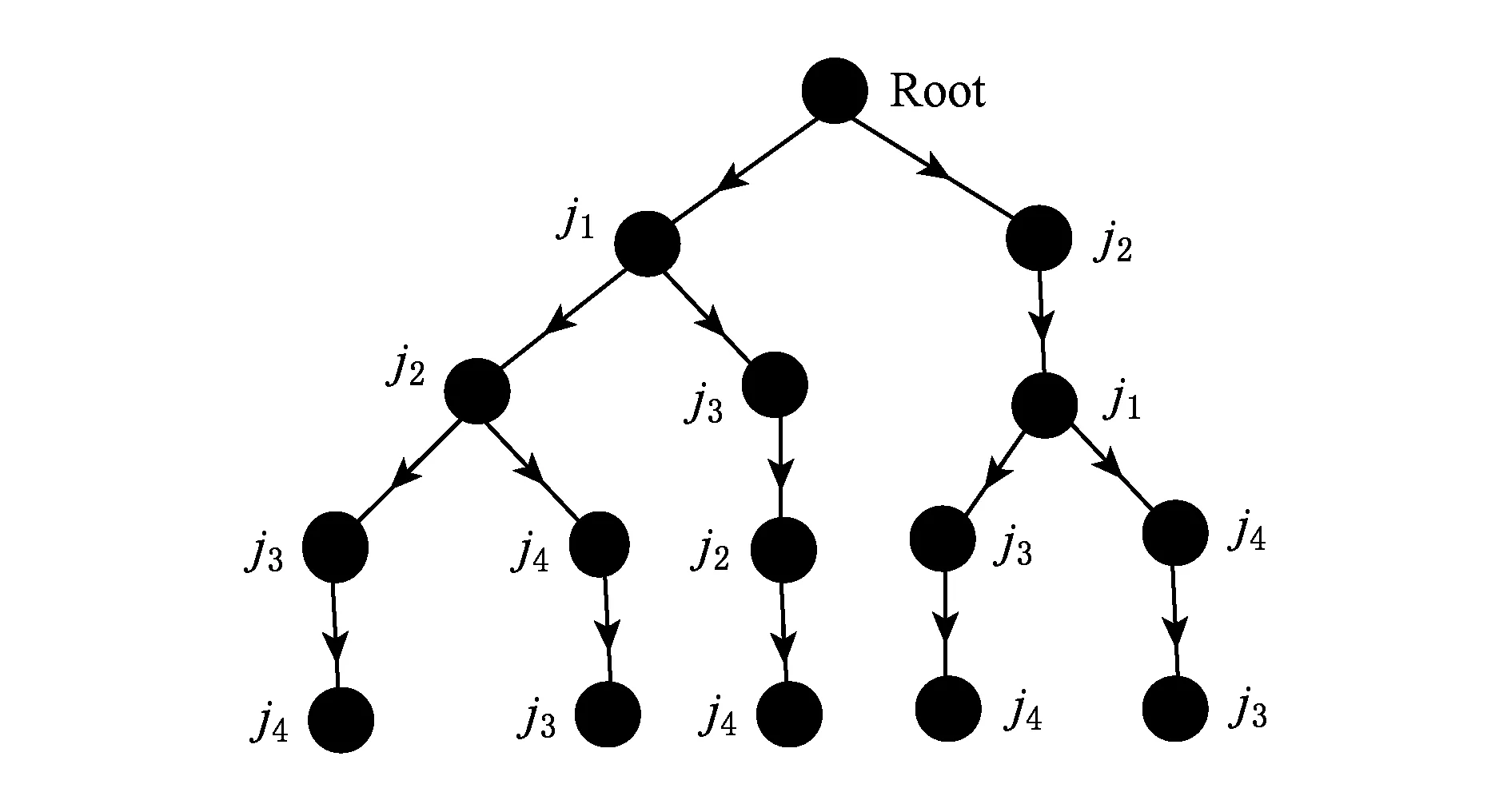
Fig. 3 Searching tree for the tasks.图3 任务的搜索树
当任务数过多、偏序关系过于复杂而且社会网络节点过多时,算法的执行效率会由于搜索树的结构过大而降低.在算法中加入分支限界策略,对不可能产生最优解的分支提前剪支可以极大地提升算法效率.
如图4所示,本文采用爬山法进行深度优先搜索,当扩展到叶节点j4时,记录当前的一个总代价值cost=6.6;当回溯到另一分枝考虑j2节点时,若当前团队的代价值cost=6.8,表示再向下扩展节点时,总代价不可能小于6.8,所以此分枝不可能产生最优解,通过分支限界法将此分枝裁剪掉.

Fig. 4 The pruned searching tree.图4 被裁剪的搜索树
在图4中,每个节点都对应着一个完成该任务的个体,然而root所对应的个体应如何选择?本文将root节点所对应的个体设定为整个团队的leader.在实际应用中leader通常由管理层指定,无需选择.但CSN-TPR问题定义中没有给出leader,需要选取leader.选取leader通常需要考虑3方面因素:1)该个体认识的成员相对较多,也就是图G中度较大的节点;2)所会任务相对较多;3)完成所会任务的平均时间相对较短.为了将这3方面因素都考虑到leader的选取中,本文又引入平衡参数γ和μ(γ,μ∈[0,1],γ+μ≤1)来平衡这3方面因素,leader选取算法伪代码如算法1所示:
算法1.leader选取算法.
输入:G(V,E),Task(V)={X1,X2,…,Xn},γ,μ;
输出:leader.
①max_power=0;
② fori∈Vdo
③Degree=节点i在图G中的度数;
④CoverRatio=10×i所会任务数/任务总数;
⑤TaskTime=10/i做所会任务平均时间;
⑥i_power=γ×Degree+μ×CoverRatio+
(1-γ-μ)×TaskTime;
⑦ ifi_power>max_powerthen
⑧max_power=i_power;
⑨leader=i;
⑩ end if


利用爬山法进行树结构搜索过程中,需要计算团队的通信代价.本文采用最小生成树的权值作为通信代价[2].为快速计算通信代价,本文对图G中每个节点到其他节点的最短距离预先计算并存储.求解CSN-TPR问题的HillClimbingTF_BBS算法伪代码如算法2所示:
算法2. HillClimbingTF_BBS算法.
输入:G(V,E),Task(V)={X1,X2,…,Xn},P(T,R);
输出:Team,Allocation.
① 初始化优先级队列Q[0],Q[1],…,Q[k]=∅,初始化Team,Allocation,V′=∅;
② 使用算法1选取leader;
③leader放入Q[0];
④Team,Allocation=HillClimbing_BBS(0,V′);
⑤ returnTeam,Allocation.
在算法2中,步骤①为初始化工作.因为在搜索树的每一层都需要1个优先级队列,存储当前任务的所有后继任务和完成后继任务的最优个体以及对应的代价,所以初始化k+1个优先级队列Q[0],Q[1],…,Q[k],其中k为任务数.Team记录算法选择的优化团队,Allocation记录为优化团队成员分配的任务以及对应的时间和预算等信息,V′记录当前构建的部分团队.步骤③调用遍历任务搜索树的递归算法HillClimbing_BBS,其伪代码如算法3所示:
算法3. HillClimbing_BBS算法.
输入:h,V′;
输出:Team,Allocation.
① ifh=kthen /*k为任务数*/
②Node=Q[h].Pop( );
③V′=V′∪Node;
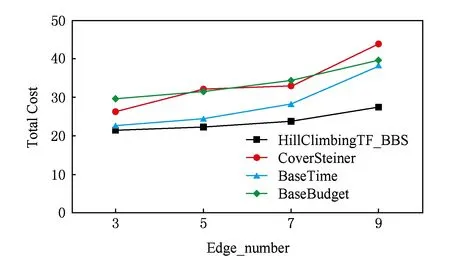
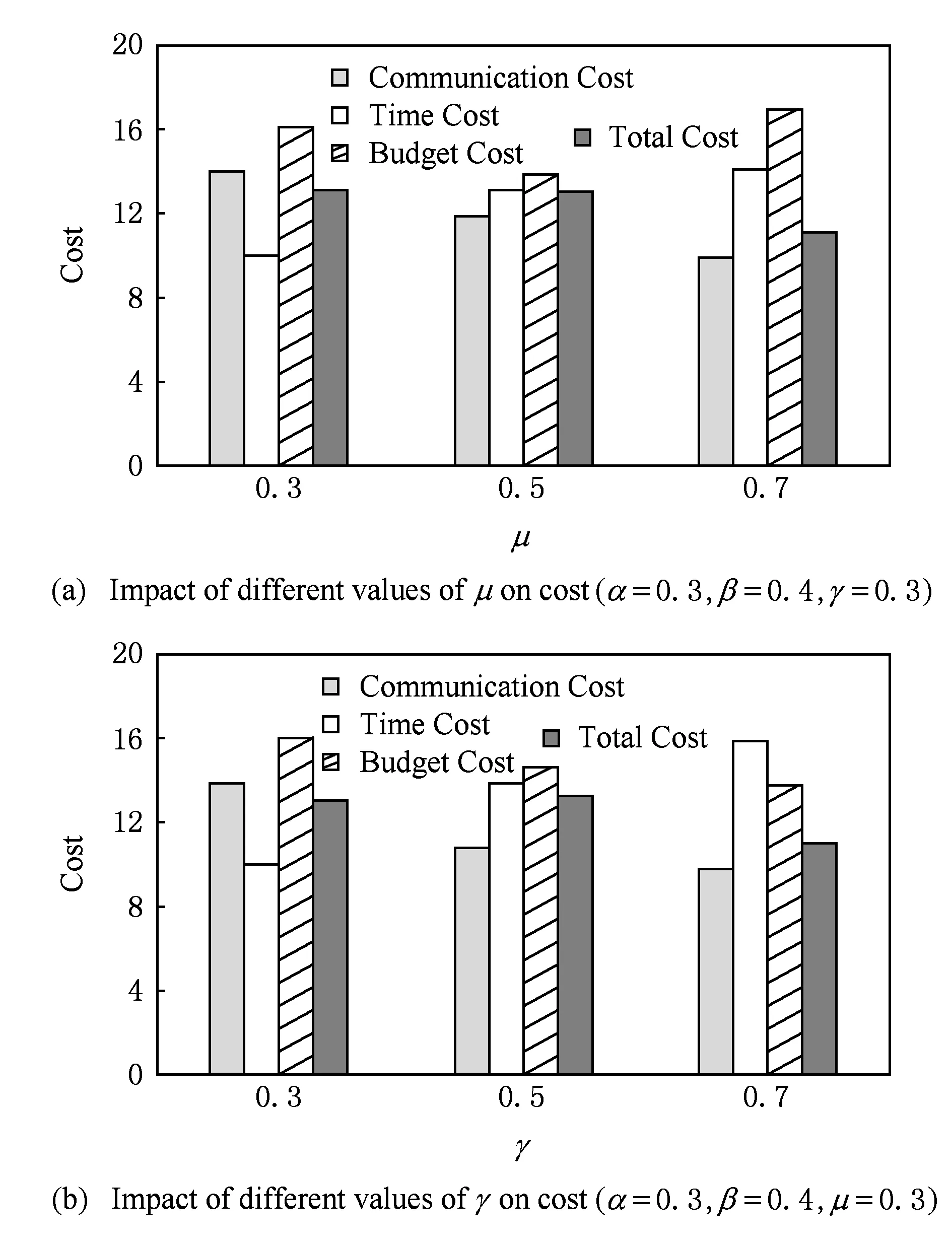
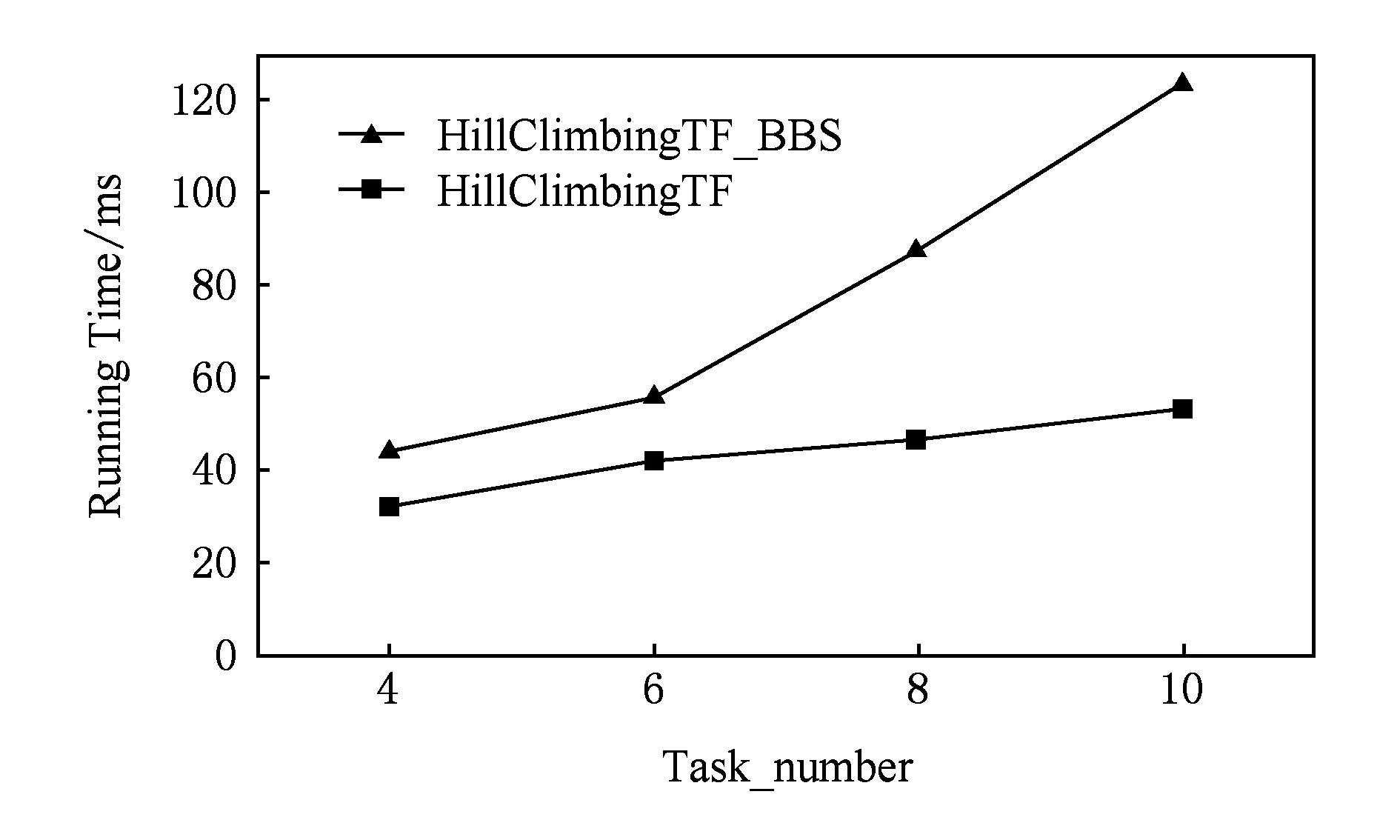
④ ifC(V′) ⑤mincost=C(V′),Team=V′; ⑥ 在Allocation中记录Node的任务、时间和预算分配; ⑦ end if ⑧h=h-1; ⑨ HillClimbing_BBS(h,V′Node); ⑩ end if 扩展*/ 节点); 4.2 动态规划求解时间代价 完成每项任务的人员一旦确定,完成每项任务的时间也就确定了.图5(a)给出了一个偏序任务集,每项任务的执行时间在任务旁边列出. Fig. 5 Tasks with partial relation and weighted graph.图5 任务偏序集和对应的加权图 由于任务之间具有严格的偏序关系,某些任务的开始执行必须在所有前驱任务完成之后,如图5(a)中j4的开始时间应为j1和j2中最后完成的时间,所以时间代价不能是最长任务的执行时间.又由于有些任务没有先后顺序可以并行执行,如图5(a)中j1和j2,所以时间代价也不应该是每项任务执行时间之和.对于具有偏序关系的任务集合,时间代价应为整个项目最后完成的时间.对图5(a)中的偏序任务集,因为j1和j2可以同时执行,j1和j2完成后才可以执行j4,所以整个项目的完成时间为3+2=5,图5(a)中的偏序任务集的时间代价等于5. 我们使用动态规划方法计算偏序任务集的时间代价.对于任何偏序任务集,可以构造一个带有源点和终点的加权图.例如:对图5(a)中的偏序任务集,构造的加权图如图5(b)所示.这时,求偏序任务集的时间代价就等价于在加权图中计算从源点S到终点T的最长路径长度.例如,计算图5(a)中的偏序任务集的时间代价等价于计算图5(b)中从源点S到终点T的最长路径长度. 设L(u,v)表示加权图中从节点u到节点v的最长路径长度.对于图5(b)中的加权图显然有: L(S,T)=max{0+L(j1,T),0+L(j2,T)}, L(j1,T)=max{1+L(j3,T),1+L(j4,T)}, L(j2,T)=max{3+L(j4,T)}. 容易验证在有向加权图中求从源点到终点的最长路径长度问题满足最优子结构,重叠子问题条件,因而可用动态规划进行求解. 设Gw表示从任务的偏序集构造的带有源点S和终点T的加权图.l表示从源点S到达终点T的最多边数.令L(u,T)表示从节点u到终点T的最长路径长度;next(u)表示从节点u到终点T的最长路径上u的后继节点.令LV(i)表示最多经过i条边到达终点T的节点集合.动态规划方法计算时间代价的伪代码如算法4所示: 算法4. 计算时间代价的算法. 输入:Gw; /*加权图*/ 输出: 源点S到终点T的最长路径长度length. ① fori=2 tol ② foru∈LV(i) ⑤ end for ⑥ end for ⑦length=0,u=S; ⑧ fori=1 tol ⑨length=length+d(u,next(u)); ⑩u=next(u); 4.3 算法复杂度分析 HillClimbingTF_BBS算法预先计算图G中每个节点到其他节点的最短距离,可以对每个节点调用DIJKSTRA算法或者直接使用FLOYD算法,时间复杂性为O(n3),其中n为图G中节点数. 在计算个体i加入当前团队V′的总代价时,需要计算通信代价、预算代价、时间代价.通信代价可以使用Prim算法计算最小生成树获得,时间复杂性为O(k2),其中k为任务数;计算预算代价只需对所有成员的薪资累加求和,时间复杂性为O(k);计算时间代价需要在偏序任务集对应的加权图上计算源点到终点的最长路径,使用动态规划方法的时间复杂性为O(n′+e′),其中n′为加权图上的节点数,e′为加权图上的边数.因为n′=k+2,e′≤k2+2k,所以计算时间代价的时间复杂性最多为O(k2).因此,计算一次总体代价的时间复杂性为O(k2). 令p表示会某个任务的平均人数.HillClimbingTF_BBS算法在遍历搜索树中的某个节点时,需要对会该任务的所有人计算总体代价,因此遍历搜索树中某个节点的平均时间复杂性为O(pk2).显然,搜索树中的节点数最多为k!,所以HillClimbingTF_BBS算法遍历整个搜索树的时间复杂性为O(k!pk2).加上计算最短距离的预处理时间,算法HillClimbingTF_BBS的时间复杂性为O(n3+k!pk2). 在实际应用中,最短距离计算可以计算一次存储起来,不需要每次都计算.任务数k通常是一个比较小的值,而且,由于采用了分支限界策略,被搜索的节点数通常要远远小于k!.因而算法HillClimbingTF_BBS在实际应用中会有很高的效率. 5.1 实验设置 偏序任务集为模拟生成的有向无环图,具体生成过程如下:1)设定偏序图中的任务数k和偏序边数e.当任务数为k时,从任务域A中随机选择k个任务作为偏序图的结点(不同的节点可以具有相同的任务).2)从这k个节点中随机选择一对不同的节点u和v,再随机确定边的方向,例如u→v.如果边u→v加入偏序图中没有形成回路,则添加边u→v到偏序图中;如果边u→v加入偏序图中形成回路,则放弃边u→v.重复上述过程,直到偏序图中包含了e条边.在后面的实验中,如果没有明确说明边数e,则边数e默认取k-1. 为了使得通信代价、时间代价和预算代价具有可比性,本文将边上权值、完成任务时间和薪资的数值单位均统一到1~10之间的数.具体过程如下:如果DBLP合作网络边上的权值ω(i,i′)在[0,0.1)区间,则设置ω(i,i′)=1;如果ω(i,i′)在[0.1,0.2)区间,则设置ω(i,i′)=2.以此类推,如果ω(i,i′)在[0.9,1)区间,则设置ω(i,i′)=10.个体完成各任务的时间和所需薪资从1~10中均匀随机生成. 所有算法用C++编写,在VC++ 6.0环境下编译.所有实验都在AMD Athlon II X4、2 GHz的CPU、8 GB内存的台式机上运行. 5.2 不同算法比较 本组实验比较不同算法产生团队的总代价.由于现有的算法不能直接求解CSN-TPR问题.我们构造如下对比算法: 1) CoverSteiner[2].在忽略偏序关系的基础上执行CoverSteiner算法求得通信代价小的团队,将所得团队中的中间连接节点去掉,只保留完成任务的个体,再将处理后的团队根据任务偏序关系进行时间和薪资的分配,并计算总代价. 2) BaseTime.只考虑时间因素求时间代价最小的团队,所获团队再计算总代价. 3) BaseBudget.只考虑薪酬因素求预算代价最小的团队,所获团队再计算总代价. α=0.3,β=0.4,γ=0.3,μ=0.4Fig. 6 Comparison of HillClimbingTF_BBS and other algorithms w.r.t different Task_number.图6 不同任务数下HillClimbingTF_BBS和其他算法的比较 以上算法计算通信代价都以最小生成树为衡量标准. 在固定平衡参数条件下,分别选取带有不同任务数的偏序任务比较不同算法产生团队的总代价,实验结果如图6所示.为了排除偶然性,对每个任务数都随机生成10组偏序任务进行实验,结果取均值. 从图6可以看出,HillClimbingTF_BBS算法所求总代价明显低于其他算法.尤其当任务数增多时,HillClimbingTF_BBS算法的优势更显著.这是由于其他算法只考虑某一方面代价的优化,而HillClimb-ingTF_BBS算法同时考虑通信代价、时间代价和预算代价3方面的优化. 5.3 偏序程度对不同算法的影响 本组实验考察偏序程度对不同算法的影响.在固定任务数k=8条件下,分别选取不同数目的偏序边从而生成不同的偏序任务,比较不同算法产生团队的总代价,实验结果如图7所示.为了排除偶然性,当偏序边数固定时,随机生成10组偏序任务进行实验,结果取均值. k=8,α=0.3,β=0.4,γ=0.3,μ=0.4Fig. 7 Comparison of HillClimbingTF_BBS and other algorithms w.r.t different Edge_number.图7 不同偏序程度下HillClimbingTF_BBS和其他算法的比较 从图7可以看出,随着偏序程度复杂化(偏序边数增多),HillClimbingTF_BBS算法所求总代价明显低于其他算法.例如:当偏序边数从7增加到9时,HillClimbingTF_BBS算法所求的总代价只增加了3个单位左右,而其他算法所求的总代价却增加了10单位以上.这是由于其他算法只考虑某一方面代价的优化,没有考虑任务之间的偏序关系.当任务集合固定时,所构造的团队也固定了.但当偏序程度变复杂时,时间上的可协调性受到更多限制,因此时间代价明显增大,总代价也随之增大.而HillClimbingTF_BBS算法同时考虑通信代价、时间代价和预算代价3方面的优化.当任务集合固定而偏序程度变复杂时,HillClimbingTF_BBS算法会考虑偏序关系优化总代价,从而会选择不同的团队,因而总代价增加得较缓慢,这说明Hill-ClimbingTF_BBS算法更适合处理偏序程度复杂化的任务集合. 当固定任务数k取4,6,10条件下变化偏序边数目时,也得到了与实验图7类似的实验结果. 5.4 任务数对分项代价影响 本组实验考察在不同任务数条件下产生团队的各分项代价以及总代价的变化.将平衡参数值固定,分别选取带有不同任务数的偏序任务进行代价值比较,为了排除偶然性,对每个任务数都随机生成10组偏序任务进行实验,结果取均值. 实验结果如图8所示,平衡参数一定,随着任务数的增多,各分项代价以及总代价都会相应增大.这是因为随着任务数的增多,任务偏序关系趋向于复杂化,所找到的团队人数增多,由此通信代价和预算代价就会相应增大,而时间上的可协调性也受到更多限制,因此时间代价也会相应增大,总代价也随之增大. α=0.3,β=0.4,γ=0.3,μ=0.4Fig. 8 Cost of each part of HillClimbingTF_BBS w.r.t different Task_number.图8 不同任务数条件下HillClimbingTF_BBS算法各分项代价 5.5 不同平衡参数对算法的影响 本组实验考察不同参数的变化对团队的分项代价和总代价的影响.在图9(a)中,固定了参数β,γ,μ的值,改变参数α的值,考察各分项代价和总代价的变化.随着α的增大,通信代价逐渐减小,预算代价逐渐增大.这是由于α的增大,通信代价在总代价中的比重逐渐增大,而预算在总代价中的比重则逐渐减小,为了使得总代价最小化,对占比重较大的通信代价限制会更严格,通信代价便逐渐减小,而预算代价限制则相对放宽,预算代价便逐渐增大. 在图9(b)中,固定了参数α,γ,μ的值,改变参数β的值,考察各分项代价和总代价的变化.随着β的增大,时间代价逐渐减小,预算代价逐渐增大.这是由于β的增大,使得时间代价在总代价中的比重逐渐增大,而预算在总代价中的比重则逐渐减小,为了使得总代价最小化,对占比重较大的时间代价限制会更严格,时间代价便逐渐减小,而预算代价限制则相对放宽,预算代价便逐渐增大. 在图10(a)中,固定了参数α,β,γ的值,改变参数μ的值,考察各分项代价和总代价的变化.随着μ值的增大,所找团队通信代价逐渐减小,时间代价逐渐增大.这是由于当μ值逐渐增大时,使得选取leader时社会网络中节点度数所占比重逐渐增大,所以由leader开始扩展的节点相对较多,所找团队通信代价逐渐减小,而由于可选个体的增多,团队在时间协调性上受到一定限制,时间代价则相应增大. 在图10(b)中,固定了参数α,β,μ的值,改变参数γ的值,考察各分项代价和总代价的变化.随着γ值的增大,所找团队通信代价逐渐减小,预算代价逐渐减小.这是由于参数γ控制了leader的任务覆盖率,随着γ值的增大,leader所会技能增多,相对地在所找到的团队中leader所做任务数相对地增多,团队人数相对地减小,总体的通信代价则会降低.由于团队人数减少,每个团队内成员可能做多个任务,影响了任务的可并行性,使得时间代价增大. Fig. 10 Impact of the variation of μ and γ on cost.图10 参数μ和γ的变化对代价的影响 5.6 分支限界策略的有效性 α=0.3,β=0.4,γ=0.3,μ=0.4Fig. 11 Running time of HillClimbingTF and HillClimbingTF_BBS w.r.t different Task_number.图11 不同任务数条件下HillClimbingTF和HillClimbingTF_BBS运行时间 为了验证分支限界策略的有效性,本节进行如下对比实验:选择没有加入分支限界策略的HillClimbingTF算法与HillClimbingTF_BBS算法进行比较.在固定平衡参数条件下,分别选取带有不同任务数的偏序任务进行算法效率对比,为了排除偶然性,对相同任务数分别取10个不同的偏序任务进行实验,实验结果取均值.如图11所示,随着任务数的增多,HillClimbingTF算法的效率大幅下降,而HillClimbingTF_BBS算法则具有很好的扩展性.因为任务数的增多使得搜索树的分支呈指数增长,HillClimbingTF算法的运行时间也随之大幅度增长;而加入分支限界策略的HillClimbingTF_BBS算法提前减去不可能产生最优结果的分支,使得搜索范围大大降低,提升了算法效率. 5.7 联机近似比 为了证明HillClimbingTF_BBS算法的有效性,本节通过实验给出算法的联机近似比.对于具体的CSN-TPR问题,我们很容易计算最优团队总代价的下界.设V*是最优团队.首先使用算法CoverSteiner[2]求得通信代价最小的团队V1,显然有Cc(V1) 设V为HillClimbingTF_BBS算法求得的团队,则联机近似比为 图12显示了当任务数变化时本文算法输出团队的总代价以及最优团队总代价的下界.实验结果表明HillClimbingTF_BBS算法的联机近似比约为1.6,由此验证了HillClimbingTF_BBS算法的有效性. α=0.3,β=0.4,γ=0.3,μ=0.4Fig. 12 Total cost of HillClimbingTF_BBS and lower ound.图12 HillClimbingTF_BBS算法总代价和总代价下界 本文首次提出了基于偏序任务的社会网络合作问题CSN-TPR,并证明了此问题为NP-hard问题.为了解决该问题,本文提出了一个高效的近似算法HillClimbingTF_BBS.实验结果验证了该算法的有效性和高效率. [1]Chen S J, Lin L. Modeling team member characteristics for the formation of a multifunctional team in concurrent engineering[J]. IEEE Trans on Engineering Management, 2004, 51(2): 111-124 [2]Lappas T, Liu K, Terzi E. Finding a team of experts in social networks[C] //Proc of the 15th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2009: 467-476 [3]Datta S, Majumder A, Naidu K. Capacitated team formation problem on social networks[C] //Proc of the 18th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2012: 1005-1013 [4]Rangapuram S S, Hler T, Hein M. Towards realistic team formation in social networks based on densest subgraphs[C] //Proc of the 24th Int Conf on World Wide Web. New York: ACM, 2013: 1077-1087 [5]Kargar M, An A, Zihayat M. Efficient Bi-Objective Team Formation in Social Networks[M]. Berlin: Springer, 2012: 483-498 [6]Arkin E M, Refael H. Minimum-diameter covering problems[J]. Networks, 1997, 36(3): 147-155 [7]Duin C W, Volgenant A, Voß S. Solving group Steiner problems as Steiner problems[J]. European Journal of Operational Research, 2004, 154(1): 323-329 [8]Baykasoglu A, Dereli T, Das S. Project team selection using fuzzy optimization approach[J]. Cybernetics and Systems, 2007, 38(2): 155-185 [9]Gajewar A, Sarma A D. Multi-skill collaborative teams based on densest subgraphs[C] //Proc of the 12th SIAM Int Conf on Data Mining. Philadelphia, PA: SIAM, 2012: 165-176 [10]Yang D N, Chen Y L, Lee W C, et. al. On social-temporal group query with acquaintance constraint[J]. Proceedings of VLDB Endowment, 2011, 4(6): 397-408 [11]Li C T, Shan M K. Team formation for generalized tasks in expertise social networks[C] //Proc of IEEE Int Conf on Social Computing. Piscataway, NJ: IEEE, 2010: 9-16 [12]Farhadi F, Hoseini E, Hashemi S M. TeamFinder: A co-clustering based framework for finding an effective team of experts in social networks[C] //Proc of IEEE Int Conf on Data Mining Workshops. Piscataway, NJ: IEEE, 2012: 107-114 [13]Sozio M, Gionis A. The community-search problem and how to plan a successful cocktail party[C] //Proc of the 16th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2010: 939-948 [14]Anagnostopoulos A, Becchetti L, Castillo C, et. al. Power in unity: Forming teams in large-scale community systems[C] //Proc of the 19th ACM Int Conf on Information & Knowledge Management. New York: ACM, 2010: 599-608 [15]Sun Huanliang, Jin Mingyu, Liu Junling, et al. Methods for team formation problem with grouping task in social networks[J]. Journal of Computer Research and Development, 2015, 52(11): 2535-2544 (in Chinese) (孙焕良, 金洺宇, 刘俊岭, 等. 社交网络上支持任务分组的团队形成方法[J]. 计算机研究与发展, 2015, 52(11): 2535-2544) Liu Yong, born in 1975. Associate professor at Heilongjiang University. Member of China Computer Federation. His main research interests include data mining and social network. Han Xue, born in 1991. Graduate student at Heilongjiang University. His main research interests include data mining and social network. Li Jinbao, born in 1969. Professor and PhD supervisor at Heilongjiang University. Senior member of China Computer Federation. His main research interests include sensor network, mobile social network and big data. Ren Qianqian, born in 1980. Associate professor at Heilongjiang University. Her main research interests include database and information processing. Wang Nan, born in 1980. PhD candidate at Heilongjiang University. Her main research interests include sensor network and social network. Collaboration Algorithm in Social Networks Based on Tasks with Partial Relation Liu Yong, Han Xue, Li Jinbao, Ren Qianqian, and Wang Nan (SchoolofComputerScienceandTechnology,HeilongjiangUniversity,Harbin150080)(KeyLaboratoryofDatabaseandParallelComputingofHeilongjiangProvince(HeilongjiangUniversity),Harbin150080) The collaboration problem in social networks has attracted lots of interests among the data mining community. Previous work focused on finding a team with the lowest communication cost to complete all tasks in a project. However, tasks in the realistic projects usually have partial ordering relations. Existing methods cannot deal with partial ordering relations, and thus are not capable of obtaining an effective team. In this paper, we study how to complete the tasks with partial ordering relations effectively, and propose a novel collaboration problem in social networks, named CSN-TPR (collaboration problem in social networks based on tasks with partial ordering relations). Specifically, we investigate how to select an appropriate team in social networks to complete the tasks with partial ordering relations so as to minimize the total cost which is composed of communication cost, time cost and budget cost. We firstly prove that CSN-TPR is NP-hard, and then adopt hill-climbing method, branch and bound strategy and dynamic programming method to propose an approximation algorithm called HillClimbingTF_BBS. HillClimbingTF_BBS can not only acquire an effective team, but also obtain the task allocation of each team member and the start time of each task. The experimental results on real data show that HillClimbingTF_BBS can solve CSN-TPR effectively and efficiently. social networks; collaboration; partial relation; hill-climbing; branch and bound 2015-06-30; 2016-03-22 国家自然科学基金项目(61370222,61300225);黑龙江省自然科学基金项目(F201430);黑龙江省高校科技创新团队建设计划项目(2013TD012);黑龙江省教育厅科技研究项目(12531476);哈尔滨科技创新人才研究专项资金项目(2012RFQXG096) 任倩倩(rqian99@163.com) TP311.1 This work was supported by the National Natural Science Foundation of China (61370222, 61300225), the Natural Science Foundation of Heilongjiang Province of China (F201430), the University Science & Technology Innovation Team Project of Heilongjiang Province (2013TD012), the Science & Technology Project of Department of Education of Heilongjiang Province (12531476), and the Innovation Talents Project of Science and Technology Bureau of Harbin (2012RFQXG096).
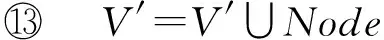
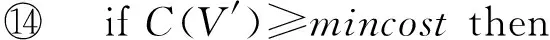
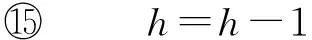




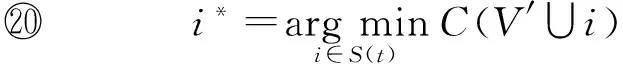













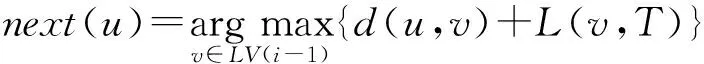
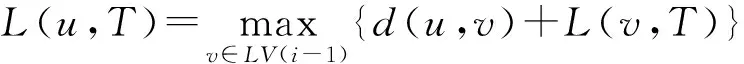


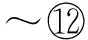
5 实验结果与分析
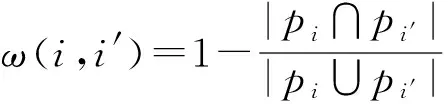




6 结束语






