基于仿生学的不相关局部保持鉴别分析
宁 欣 李卫军 李浩光 刘文杰
(中国科学院半导体研究所 北京 100083) (ningxin@semi.ac.cn)
基于仿生学的不相关局部保持鉴别分析
宁 欣 李卫军 李浩光 刘文杰
(中国科学院半导体研究所 北京 100083) (ningxin@semi.ac.cn)
由于形象思维方式是人类的一种本质思维方式,人类通过各种感官来认知事物的规律性,进而提取出具有代表性的特征,因此通过形象思维的方法来提取事物的本质特征符合人类认知事物的规律.针对人脸识别中特征提取问题,该算法以形象认知规律与无监督判别投影为理论基础,提出了一种仿生不相关空间局部保持鉴别分析(biomimetic uncorrelated locality preserving discriminant analysis, BULPDA)算法.算法首先根据人类形象认知的特性构建了一种新的相似系数表示方法;然后结合不相关空间概念,确保矢量空间具有不相关性;最后给出了基于奇异值分解的矢量空间求解方法,形成了一种特征提取新思路.在标准数据库上的实验结果表明,新算法优于传统的特征提取方法和其他改进的局部保持投影方法.
无监督判别投影;形象认知;不相关空间;特征提取;奇异值分解
在基于子空间分析的方法中,He等人[1]提出的局部保持投影 (locality preserving projection, LPP) 算法是一种经典特征提取算法,该算法由于考虑了样本的流形结构,在模式识别中取得了较好的识别效果,因而得到了关注,并从不同角度提出了改进的算法,均取得了较好的识别效果[2-8];文献[2]给出了LPP在应用于高维小样本时的具体求解框架;文献[3]则针对LPP数值解的稳定性进行了研究,给出了一种稳定的求解模型;文献[4]则针对LPP中的相似矩阵进行了研究,给出了一种优化相似矩阵的LPP;但上述改进方法并没有从分类的角度考虑问题,文献[9]提出的无监督判别投影(unsupervised discriminant projection, UDP)算法更适合分类,该方法目标函数类似于Fisher线性鉴别分析,使得投影后同类样本相互靠近,非同类样本相互远离,但是该方法没有用到样本间的类别信息,当人脸图像的表情、姿态等发生较明显变化时,算法的识别性能会明显下降;因此,后续有很多基于UDP算法的改进[10-11],文献[11]提出了一种基于Fisher的保局投影(Fisher locality preserving projections, FLPP)算法,改善了算法的识别性能,但是未考虑到类别内部与不同类之间的规律.
总而言之,现有的特征提取技术是从逻辑思维的方法来解决形象思维的问题,但是以定理、推论等手段的逻辑思维方法很难反映人类认知过程的本质性.而形象思维方法是人的一种本质思维方式,通过人的各种感官来认知事物的规律性,进而提取出具有代表性的特征,因此形象思维的问题通过形象思维的方法来解决是具有优势的.另一方面,上述方法所求的鉴别矢量之间不具有不相关性,在特征提取理论中,通常希望所获得的鉴别矢量相关性越低越好,从而提高识别率.本文结合人类形象思维的特性提出了一种仿生不相关局部保持鉴别分析(biomimetic uncorrelated locality preserving discriminant analysis, BULPDA)算法.BULPDA算法以UDP算法为理论基础,根据形象思维的特性提出了一种新的相似系数构造方法,不仅利用了样本间的类别信息,而且反映了同类样本之间的规律和不同类样本间的相似性;另外,BULPDA算法引入了不相关空间,使得最终的矢量集具有不相关性,不仅进一步发展了UDP算法,而且形成了一种特征提取的新思想和新方法.
1 无监督判别投影
UDP算法[9]是对LPP算法的改进,其目标函数类似于Fisher线性鉴别分析,因此,相比于LPP算法,UDP算法更加适合分类,但是仍然没有用到类别信息.样本空间X=[x1,x2,…,xi],每个xi代表一幅人脸图像,首先给出UDP算法中局部散度矩阵SL、非局部散度矩阵SNL与总体散度矩阵Stotal的定义为
(1)
(2)
(3)
式(1)与式(2)中的相似系数si j计算为
(4)
局部散度矩阵SL与非局部散度矩阵SNL类似于Fisher线性判别分析中的类内散度矩阵和类间散度矩阵,但是并没有用到样本的类别信息.UDP算法的目标函数为
(5)
或者
(6)

(7)
或者

(8)
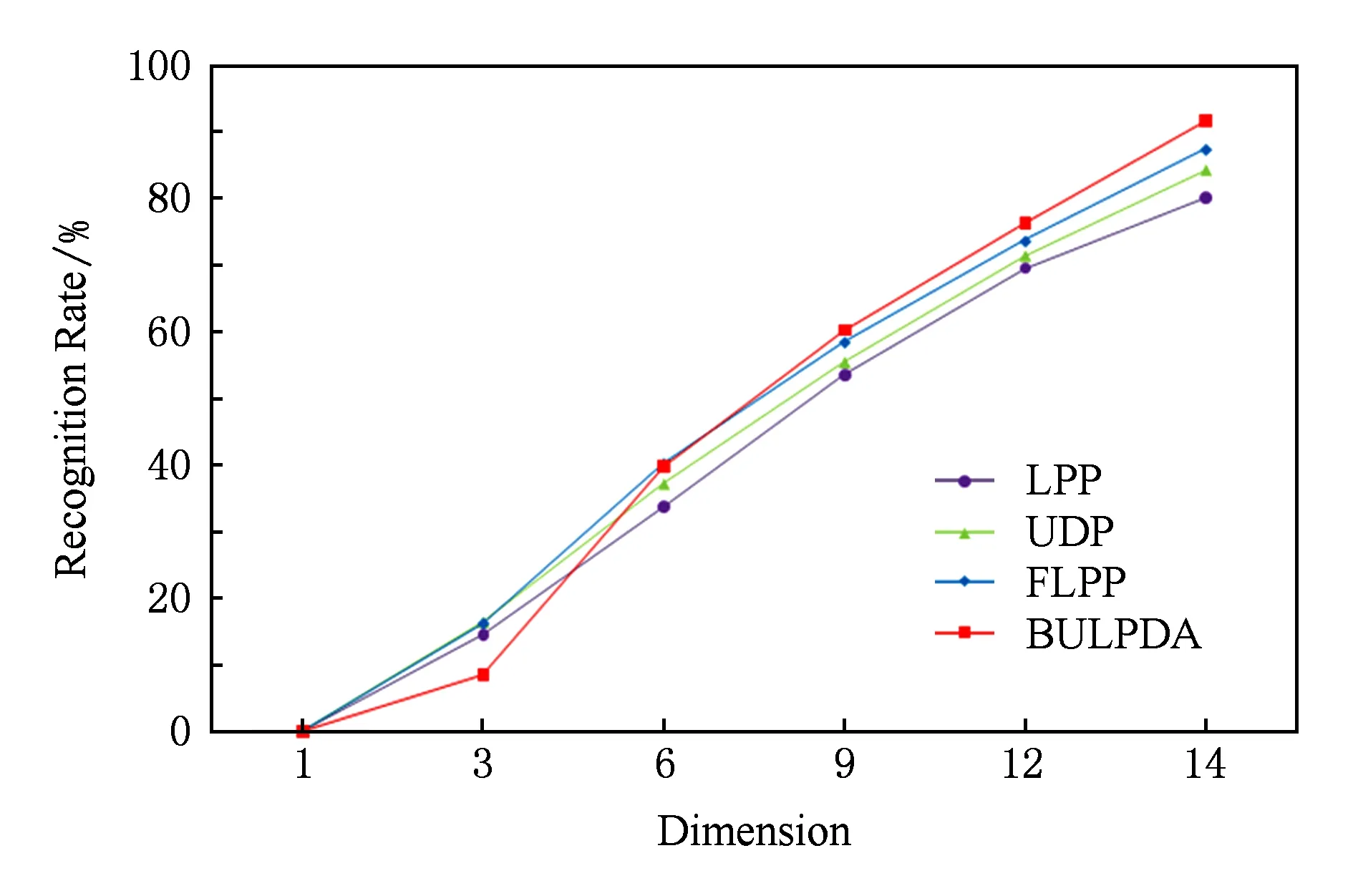
假设把求得的特征值按降序排列λi≥λi+1,选择对应前d(通常d 2.1 仿生形象思维特性 仿生形象思维方法应用于信息科学领域以来,成功地应用于模式识别等多领域[12-14].相对于用逻辑思维方法来解决信息科学领域问题,以形象思维方法研究为基础的方法,是目前解决图像处理、语音识别等形象思维问题的有效方法.本文算法主要是依据2个形象思维特性: 1) 同源连续性 来源于同一个事物并表征其不同状态的样本,称为同源样本.一般情况下,2个同源样本α1与α2之间至少存在1条连续的通道η,该通道中的每一个点均属于α1与α2的同源样本,使得样本α1沿着通道η所表示的是一个连续渐变的过程,可以逐步演变为同源样本α2.同源样本之间所存在的上述内在规律,我们称之为同源连续性规律(principle of homology continuity, PHC)[15-16]. 2) 异源相似性 2个不同类的样本存在着一定的相似性.从人类形象认知方面出发,假设人区分1只狗和1只羊的认知难度为β1,区分1只狗和1只狼的认知难度为β2,那么很显然有β1>β2,因为狗与狼之间的相似性大于狗与羊的相似性,更加难以区分.因此,一个样本点和不同的异类样本点之间的相似性是不同的,相似性的量化值是渐变的,这个关于异源的样本间的相似性规律,我们称之为异源相似性原理. 传统的模式识别方法做训练时,将训练样本严格分为正样本和负样本,但是并未考虑到正样本内在的规律,也没有考虑到正样本与负样本之间的联系,因此,并不符合人类形象思维的认知过程. 2.2 BULPDA算法描述 在上述UDP算法中的局部散度矩阵SL和非局部散度矩阵SNL均用到了相似系数si j,si j表示样本xi与样本xj之间的相似关系.LPP算法中,si j构成近邻矩阵S表示不同样本之间的位置相似权值.但是,算法UDP与LPP均未用到样本间的类别信息,只是利用样本的近邻关系来构造相似系数.文献[7]用到了类别间的信息,但是未考虑到类别内部的同源连续性与不同类之间的异源相似性.在此,给出按照形象思维特征构造的相似系数hi j: 若xi与xj为同类样本,则: (9) 若xi与xj为不同类样本,则: (10) 其中,t为可调参数,取值范围为0 (11) 显然式(11)可以等价于 (12) 此时目标函数中的W没有任何限制,然而在特征提取理论中,一般希望获得的鉴别矢量空间相关性尽可能小,最好是不相关的,从而提高算法的识别率.下面给出不相关鉴别空间的定义. 根据定义1可知若使W具有不相关性,需满足: (13) 综合式(12)与式(13)可得最优函数为 (14) 2.3 BULPDA算法的求解 由于最终的鉴别矢量W=(w1,w2,…,wr)之间具有不相关性,所以存在1个不相关空间P,使得PTStotalP=I.BULPDA算法求解的关键一步是不相关空间的构造,下面给出不相关空间P的构造过程. 首先对Stotal进行奇异值分解,由于Stotal为对称的半正定矩阵,根据矩阵定理可被分解为 (15) 其中,U和V分别为正交矩阵,Σ2m是按照降序排列的对角矩阵,m=rank(Stotal).令U=(U1,U2),U1∈n×m,U2∈n×(n-m),n为样本的维数.U1为Stotal非零特征值对应的特征向量,令,则有: (16) 由于P满足不相关空间的定义,故P即为所求的不相关空间. P为Stotal经过奇异值分解后得出的不相关空间,P∈m×m;Q为进行特征值分解后前r个最大特征值对应的特征向量,Q∈m×r.令W=PQ,其中QTQ=Ir,r为最终选取特征的个数,则式(14)可以转化为 (17) (18) 综上所述,关于BULPDA算法的具体实现步骤如下: 1) 根据式(9)和式(10)计算出具有形象思维特性的相似系数hi j,并将其线性归一化为0~1范围之间; 3) 对Stotal进行奇异值分解,然后求出不相关空间P; 6) 令W=PQ=[w1,w2,…,wr],即W为所求的仿生不相关局部保持鉴别矢量集. 为了验证BULPDA算法的性能,在YALE和CMU PIE数据库上进行了实验,为了尽可能地避免识别部分的干扰,采用最近邻分类器进行分类. YALE人脸库中人脸图像光照表情变化较大,该人脸库包含15个人的165幅图像,每人11幅图像,每人的每幅图像均是从不同的视角获得,有较大的表情变化、光照变化以及部分缺损,每幅图像的分辨率为100×100,图1为YALE人脸库的部分图像.CMU PIE数据库包含68个人的41 368张人脸图片,采集于不同的姿态、表情和光照条件.在本实验中我们选取了C29子集的1 632张图片作为实验图像,一共68个人,每个人24张图像.图2为CMU PIE人脸库的部分图像. Fig. 1 11 samples of YALE face database.图1 YALE人脸库11个样本 Fig. 2 24 samples of CMU PIE face database.图2 CMU PIE人脸库24个样本 3.1 特征维数实验及结果分析 人脸识别的识别率主要受到样本维数与所提取的特征维数的影响.本实验中,为了验证算法的有效性,我们在YALE和CMU PIE数据库上分别选取2个数据库中前n张图像作为训练样本(YALE数据库选6张,CMU PIE数据库选14张),剩余图像作为测试样本.实验发现,FLPP算法与BULPDA算法最大特征个数取C-1时效果最佳(C为样本类别数),因此,在下面实验中,各算法的最大特征个数都取为C-1.将BULPDA,LPP,UDP,FLPP[11]算法在提取不同特征数目时的识别性能进行了比较,结果如图3和图4所示: Fig. 3 The recognition rate of four algorithms in YALE database.图3 YALE人脸库上4种算法的性能比较 Fig. 4 The recognition rate of four algorithms in CMU PIE database.图4 CMU PIE人脸库上4种算法的性能比较 从图3与图4可知,总体上来看,随着特征数目的增加4种算法的识别率都有明显的提升.算法FLPP与BULPDA无论在YALA数据库上还是CMU PIE数据库上最佳识别率都高于算法LPP与UDP,这是因为二者利用到了样本间的类别信息,属于有监督.另外,可以发现,算法BULPDA在特征数目比较少时优势并不明显,但是随着特征数目的增加识别率快速上升,最终高于其他3种算法,这是由于算法BULPDA提取的矢量空间具有不相关性,随着特征数目的增加,这种优势会更加明显. 3.2 不同样本个数实验及结果分析 不同的样本个数对算法的识别率也有较大影响,为了消除算法BULPDA识别结果的偶然性,每次实验中,在YALE和CMU PIE数据库中分别随机选取n幅图像作为训练样本,剩余图像作为测试样本,每组实验重复进行10次,取平均值作为实验结果.为了验证基于仿生特性相关系数的有效性,将UDP算法中的相关系数更换为本文基于仿生学的相关系数构造方法,求解过程不变,构成BUDP(biomimetic unsupervised discriminant projection)算法.将算法BULPDA与算法LPP,UDP,FLPP,BUDP在取不同样本个数时的识别性能进行了比较,结果如表1与表2所示. Table 1 The Recognition Rate of Five Algorithms in YALE Database Table 2 The Recognition Rate of Five Algorithms in CMU PIE Database 由表1与表2可知,总体上5种算法的识别率随着样本数量的增高而增高.可以看出,BUDP算法在2个数据库中取不同样本时的识别率均高于UDP算法,说明了基于仿生学的相关系数构造方法比传统的构造方法更加有效;BULPDA算法的识别率均高于另外4种算法,但是本文算法在多样本下的优势比少量样本情况下更明显.例如,在YALA数据库中,样本数为6时BULPDA算法识别率比FLPP算法高4.2%,样本数为3时BULPDA算法识别率比FLPP算法高0.6%,说明算法在多样本情况下优势更明显,因为多量样本数据规律性更加明显,少量样本数据规律难以提取,这也符合人类分类认知的规律. 本文讨论了UDP算法以及其他LPP改进算法的特点与不足,并在此基础上提出了一种仿生不相关局部保持鉴别分析算法BULPDA.本文算法根据人类形象认知的特性提出了一种新的相似系数构建方法,并且引入了不相关空间概念,使得最终求得的鉴别矢量空间具有不相关性,最后给出了具体的求解过程.YALE与CMU PIE人脸库上的实验结果也验证了算法的有效性.尽管本文算法具有一定优势,但是其本质是一种有监督算法,在现实问题中往往很难获得大量有类别标签的样本,因此如何充分利用无标签样本,即将算法拓展为一种半监督算法是我们下一步研究的重点. [1]He Xiaofei, Yan Shuicheng, Hu Yuxiao, et al. Face recognition using Laplacianfaces[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2005, 27(3): 328-340 [2]Zhang Yinling, Yang Fan, Zhao Xuetang. An improved LPP algorithm[C] //Proc of the 21st Int Conf on Niu Jing Systems and Infomatics. Piscataway, NJ: IEEE, 2012: 664-668 [3]Xu Yong, Song Fengxi, Feng Ge, et al. A novel local preserving projection scheme for use with face recognition[J]. Expert Systems with Applications, 2010, 37(9): 6718-6721 [4]Zhang Limei, Qiao Lishan, Chen Songkan. Graph-optimized locality preserving projections[J]. Pattern Recognition, 2010, 43(6): 1993-2002 [5]Lin Yu’e, Li Jingzhao, Liang Xingzhu. Direct orthogonal discrimination locality preserving projections method[J]. Journal of Optoelectronics·Laser, 2012, 23(3): 561-565 (in Chinese) (林玉娥, 李敬兆, 梁兴柱. 直接正交鉴别保局投影算法[J]. 光电子·激光, 2012, 23(3): 561-565) [6]Wang Qingjun, Zhang Rubo, Pan Haiwei. Face recognition based on kernel orthogonal local discrimination embedding[J]. Journal of Optoelectronics·Laser, 2010, 21(9): 1386-1389 (in Chinese) (王庆军, 张汝波, 潘海为. 基于核正交局部判别嵌入的人脸识别[J]. 光电子·激光, 2010, 21(9): 1386-1389) [7]Dornaika F, Assoum A. Enhanced and parameterless locality preserving projections for face recognition[J]. Neurocomputing, 2013, 99(1): 448-457 [8]Lin Guojun, Xie Mei. A face recognition algorithm using Gabor wavelet and orthogonal locality preserving projection[C] //Proc of 2012 Int Conf on Computational Problem-Solving. Piscataway, NJ: IEEE, 2012: 320-324 [9]Wong W, Zhao Haitao. Supervised optimal locality preserving projection[J]. Pattern Recognition, 2012, 45(1): 186-197 [10]Yang Jian, Zhang Dong, Yang Jingyu, et al. Globally maximizing, locally minimizing: Unsupervised discriminant projection with applications to face and palm biometrics[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2007, 29(4): 650-664 [11]Yang Wankou, Sun Changyin, Zhang Lei. A multi-manifold discriminant analysis for image feature extraction[J]. Pattern Recognition, 2011, 44(8): 1649-1657 [12]Wang Guoqiang, Shu Yunxing, Liu Dianting. Fisher locality preserving projections for face recognition[J]. Journal of Computational Information Systems, 2013, 9(8): 2993-3000 [13]Wang Shoujue, Lai Jiangliang. High dimensional imagery geometry and it’s applications[J]. Chinese Journal of Electronics, 2006, 15(4): 761-767 [14]Zhou Quanqiang, Zhang Fuzhi. Ensemble approach for detecting user profile attacks based on bionic pattern recognition[J]. Journal of Computer Research and Development, 2014, 51(4): 789-801 (in Chinese) (周全强, 张付志. 基于仿生模式识别的用户概貌攻击集成检测方法[J]. 计算机研究与发展, 2014, 51(4): 789-801) [15]Yang Guowei, Wang Shoujue, Wei Chengbing. Pattern classification neural network model based on homologue connectedness[J]. Acta Electronica Sinica, 2013, 41(1): 52-55 (in Chinese) (杨国为, 王守觉, 卫成兵, 等. 基于同源的同类事物连通本性的模式分类神经网络模型[J]. 电子学报, 2013, 41(1): 52-55) [16]Wang Shoujue, Lai Jiangliang. First Step to Multi-Demensional Space Biomimetic Informatics[M]. Beijing: National Defence Industry Press, 2008 Ning Xin, born in 1989. PhD candidate in the Institute of Semiconductors, Chinese Academy of Sciences. His main research interests include machine learning, digital image processing and pattern recognition. Li Weijun, born in 1975. PhD and Professor in the Institute of Semiconductors, Chinese Academy of Sciences. His main research interests include machine learning, pattern recognition and intelligent system. Li Haoguang, born in 1981. PhD candidate in the Institute of Semiconductors, Chinese Academy of Sciences. His main research interests include machine learning, digital image processing and pattern recognition. Liu Wenjie, born in 1989. PhD candidate in the Institute of Semiconductors, Chinese Academy of Sciences. His main research interests include machine learning, digital image processing and pattern recognition. Uncorrelated Locality Preserving Discriminant Analysis Based on Bionics Ning Xin, Li Weijun , Li Haoguang, and Liu Wenjie (InstituteofSemiconductors,ChineseAcademyofSciences,Beijing100083) Imagery thinking model is an essential way of thinking for human being. It cognizes the regularity of things through various human senses, and then extracts the representative features. Therefore, using the method of imagery thinking to extract the essential characteristics of things is in conformity with the law of human cognition. According to the problem of feature extraction in face recognition technology, we propose an uncorrelated space locality preserving discriminant analysis algorithm—BULPDA based on the theory of unsupervised discriminant projection and image cognitive law. On the basis of the characteristics of human image cognitive, the proposed algorithm first builds a new construction method of similarity coefficient. Then, it applies uncorrelated space concepts to ensure the non-relevance of vector space. Finally, it gives the solution of the proposed algorithm based on singular value decomposition. The algorithm presents a new idea of feature extraction. The experimental results on the standard face database show that the proposed algorithm is better than the traditional preserving projection algorithms. unsupervised discriminant projection; image cognitive; uncorrelated space; feature extraction; singular value decomposition 2015-07-02; 2015-11-19 国家自然科学基金项目(90920013,61572458);国家公派访问学者项目(201404910237);国家重大科学仪器设备开发专项项目(2014YQ470377) 李卫军(wjli@semi.ac.cn) TP391.4 This work was supported by the National Natural Science Foundation of China (90920013,61572458), the China Scholarship Council (201404910237), and the National Key Scientific Instrument and Equipment Development Project (2014YQ470377).2 不相关空间局部保持鉴别分析
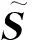


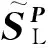
3 实验和分析





4 总 结





