蒸发冷却器的流场仿真与优化设计
钟星立++张波++张斌
摘要: 针对蒸发冷却技术相关理论模型并未完全成熟的问题,通过计算流体力学方法模拟转炉煤气干法除尘系统中蒸发冷却器的工作过程.仿真采用离散相模型(Discrete Phase Model,DPM),并在分散相液滴上应用蒸发换热模型.通过该数值方法优化该干法除尘系统中蒸发冷却器的喷淋布置方案,减少壁面的高温区域,提高温度的均匀性,使出口最高温度偏差由18.6%降低至3.4%.
关键词: 转炉; 蒸发冷却器; 离散相模型; 蒸发换热模型; 喷淋布置方案; 优化
中图分类号: TF341.1 文献标志码: B
0 引 言
蒸发冷却器是一种将水冷与空冷、传热与传质过程融为一体且兼有两者之长的高效节能冷却设备,具有结构紧凑、传热效率高、投资省、操作费用低,以及安装和维护方便等优点,被广泛应用于化工、冶金、建筑等领域.该设备的工作原理是向不饱和气体喷洒液态水,通过水与气体的接触换热以及水的蒸发吸热迅速降低气体温度.
蒸发冷却理论的形成可上溯到18世纪道尔顿提出的蒸发理论.1952年,CHUKLIN提出一种关于蒸发式冷却器管内制冷剂冷凝设计的普遍化方法,并将蒸发冷却技术应用于工业制冷,蒸发冷却器从此正式走向工艺化应用阶段.此后,众多专家学者通过多种组合实验总结出一系列传热膜系数的经验公式,初步完善蒸发冷却器的工程应用参考.[1-2]20世纪80年代以来,对蒸发冷却器的强烈需求和计算机应用技术的飞速发展,使得蒸发冷却理论和模拟研究达到新的高度.WEBB[3]较早推出统一的蒸发冷却理论模型,采用不同的相关系数区分水膜的传热系数和通过水膜传递给空气流的传质系数.随后,包括PASCAL等[4]很多人都提出自己理论模型,但到目前为止,尚没有一种获得公认的蒸发冷却换热机理的准确模型.除运用传热传质理论来分析蒸发冷却过程外,BORIS[5]和QURESHI等[6]从热力学角度研究蒸发换热模型,在系统性能评价上获得良好的效果,但并没有从根本上改变目前理论模型难以准确表述传热传质过程的窘境.
尽管蒸发换热的精确模型还有待更进一步研究,但采用现有模型的相关模拟已被大量应用,如FOUDA等[7]、QURESHI等[8]和WU等[9]都对蒸发冷却器进行数值仿真研究.然而,目前的研究大部分都集中在空调制冷方向,对于大型的工业高温气体冷却研究较少.本文针对目前钢铁冶金领域广泛应用的转炉煤气干法除尘系统中的蒸发冷却器进行仿真分析,并对该系统特有的流场结构下的喷淋布置方案进行优化.
1 数值方法
转炉煤气干法除尘系统是指在转炉钢水吹炼过程中,烟气由活动烟罩捕集并经余热锅炉冷却至1 273 K左右的转炉煤气,首先进入蒸发冷却器降温、调质和粗除尘,温度降至473 K左右后,进入静电除尘器进行精除尘;经过精除尘后的煤气,根据其品质及生产状况回收或放散.[10]在该系统的蒸发冷却器中,高压液态水经设备入口附近的喷枪喷洒到高温气体中,高压作用下的液态水在喷口形成雾化液滴.此过程中液态水滴所占体积很小,故可仅考虑气相对液滴的作用,忽略由于液滴体积和运动对气相造成的能量和动量影响.因此,本文采用离散相模型(Discrete Phase Model,DPM)模拟气-液两相流动,并在分散相液滴上应用蒸发换热模型,在DPM中选择雾化器模型.
1.1 连续相控制方程
1.2 离散相控制方程
1.2.1 离散相运动方程
1.2.2 离散相的传热和传质模型
当液滴温度低于蒸发温度时,采用热平衡方程关联液滴温度Tp与其表面的对流传热[11],即
1.2.3 两相间的耦合
在计算液滴运动轨迹的同时,跟踪计算液滴沿轨道运动的热量、质量和动量的得失,并将这些量作用于随后的连续相计算中.交替求解离散相与连续相的控制方程,直到二者均收敛为止,实现双向耦合计算.
2 应用算例
2.1 计算模型
以某钢厂200 t级转炉蒸发冷却器为研究对象,其入口直径为3.825 m;U型段在水平方向上投影长度为7 m,直径与入口直径相同;喷枪位于U型段末端,本体直筒高为21 m,直径为5.224 m.蒸发冷却器三维模型及网格划分示意见图1.
按照传统设计方法,18个喷枪在圆周方向上均匀布置,喷枪之间的角度间隔θ=20°,见图2,其中:1,2,17和18号喷枪的插入深度为945 mm, 其他喷枪插入深度为600 mm.
喷枪喷管直径为315 mm,喷嘴直径为420 mm.喷管工作压力为0.3 MPa.假设喷嘴在0.3 MPa压力条件下冷却水完全雾化且液滴呈30°实心圆锥体状喷出,以此作为DPM模型的入口边界条件.
计算网格采用完全结构化网格,对喷嘴附近区域局部加密,网格数约为120万个,最小网格尺寸约10 mm,远小于喷嘴直径.
由于系统庞大,蒸发冷却器被布置在一个180°的管道弯头后,进入蒸发冷却器的气流受此弯头影响会明显向弯管外侧偏斜,传统喷枪均匀布置方案必然无法达到理想的冷却效果,因此必须优化设计蒸发冷却器上18个喷枪的雾化喷口方案,保证蒸发冷却器出口温度均衡为473±20 K,否则会影响下一步静电除尘器工作;另外,还要尽量减少蒸发冷却器上端壁面的高温(>573 K)区域,以减少该区域耐高温材料的使用量,降低成本.
2.2 计算工况及边界条件
入口条件:煤气流量为105 N·m3/h,温度为1 273 K,密度为1.362 kg/m3,定压比热容为1.518 kJ/(m3·K),导热系数为0.022 2 W/(m·K),动力黏度为1.61×10-5 Pa·s.出口为压力出口边界条件,表压为-150 Pa.壁面为无滑移边界条件.
DPM喷射条件为:(1)水流质量入口12.795 18 kg/s,18个喷枪均分该水量;(2)根据设备厂家提供的参数,蒸发冷却器中的喷枪喷洒出的平均喷射粒径为60 μm;(3)液滴温度为306 K.
2.3 计算结果及分析
对不喷洒液滴情况下的蒸发冷却器流场进行仿真,结果见图3.由此可知:蒸发冷却器入口前的U型弯管对煤气的速度分布产生很大影响,导致煤气流量在蒸发冷却器入口截面上分布不均匀,流动在弯管外侧明显较强而在内侧很弱,这就要求在流动较强一侧设置更大的喷淋量.
通过反复调整喷枪布置并对比仿真结果,得到一种优化方案,见图4.图中编号对应的线条代表喷枪的位置和插入深度(具体数值见表1).该优化方案的模拟结果见图5,喷枪在蒸发冷却器右侧密集,使得右侧高温得到一定缓解,入口下方7 m处壁面最高温度为562 K,入口下方6 m处壁面最高温度为595 K,高温区域集中在蒸发冷却器入口下方7 m的范围内.
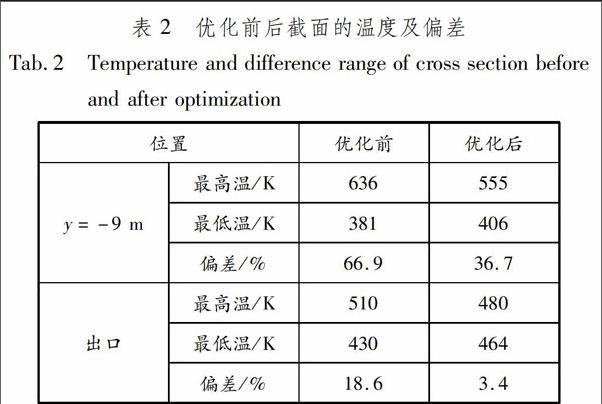
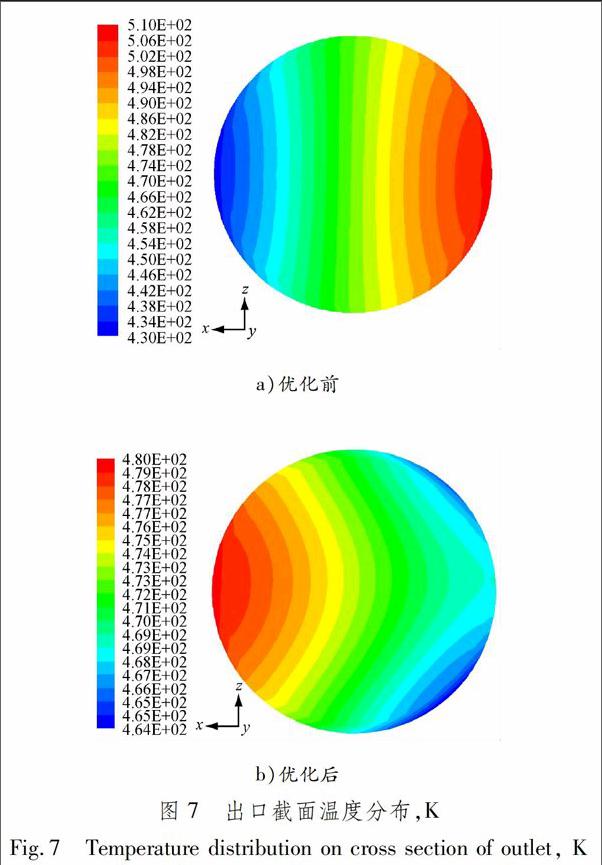
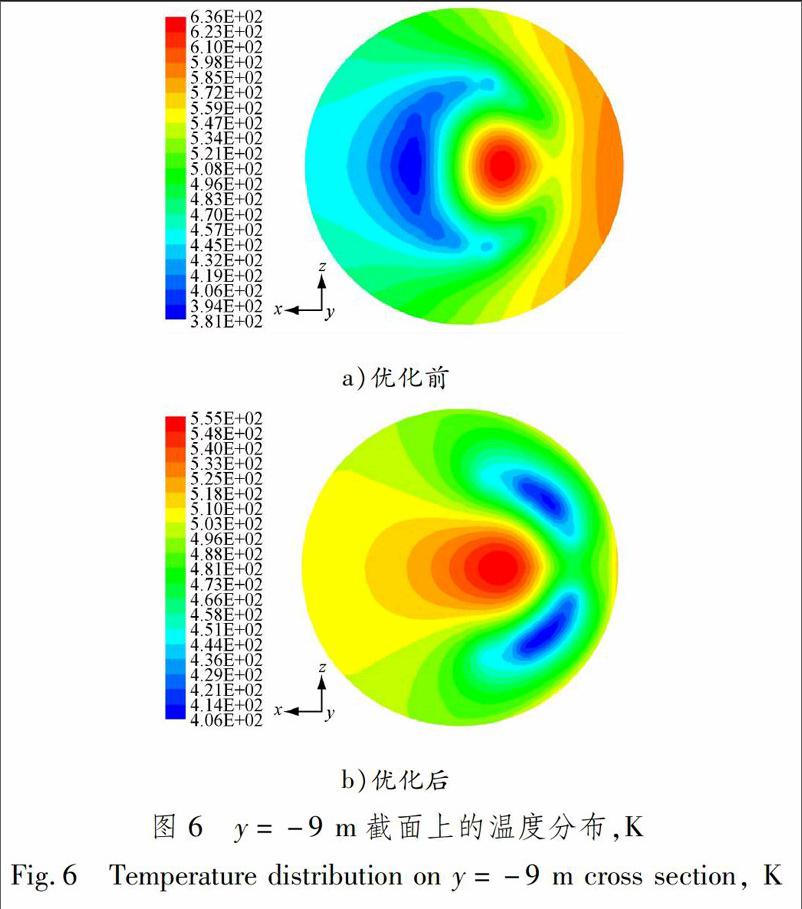
优化前后截面y=-9 m和出口的温度场比较见图6和7.优化前后截面的温度及偏差范围(定义为((最高温-最低温)/最低温)×100%)见表2.
由图6和7及表2可以看出:通过仿真优化,截面温度不均匀性得到明显改善,出口处温度由优化前的473±40 K,缩小至473±9 K范围以内,满足473±20 K的设计要求;出口截面左侧温度高于右侧,说明如果进一步增强右侧的喷淋强度,虽然可以减少蒸发冷却器壁面高温区域,但出口右侧的温度可能会过低,甚至有可能导致机械水的产生,不满足设计要求.优化后其他截面的温度分布见图8和9,各截面的最低温度均超过373 K,因此可以判断流场不存在机械水.
蒸发冷却器中按照温度渲染的喷淋液滴的流动迹线见图10.由此可知,喷淋液滴全部蒸发,没有碰到内壁,不易引起湿壁和积灰结垢.
3 结 论
采用DPM对转炉干法除尘系统中蒸发冷却器的工作过程进行模拟,成功将蒸发换热模型施加在离散液滴上.通过该数值方法对某干法除尘系统中蒸发冷却器的喷淋布置方案进行优化,蒸发冷却器出口温度偏差范围由原设计方案的18.6%降低至3.4%,满足473±20 K设计要求;同时,蒸发冷却器壁面的高温区域减小,从而降低制造成本,提高系统的运行性能.
需要指出的是,由于工程尚未投产,缺乏实际生产运行数据,本文采用的数值计算方法有待进一步确认.待条件成熟,可结合测试数据对该方法进行验证与优化,为未来蒸发冷却器的持续改进与方案创新提供支撑.
参考文献:
[1] 朱冬生, 涂爱民, 蒋翔, 等. 蒸发式冷凝冷却设备的研究状况及其应用前景分析[J]. 化工进展, 2007, 26(10): 1404-1409. DOI: 10.3321/j.issn:1000-6613.2007.10.008.
ZHU D S, TU A M, JIANG X, et al. Research progress and application prospect analysis of evaporative condensing/cooling equipment[J]. Chemical Industry and Engineering Progress, 2007, 26(10): 1404-1409. DOI: 10.3321/j.issn:1000-6613.2007.10.008.[2] 尾花英郎. 热交换器设计手册[M]. 3 版. 徐中全,译.北京: 化学工业出版社, 1973: 300-355.
[3] WEBB R L. A unified theoretical treatment of thermal analysis of cooling towers, evaporative condensers, and fluid coolers[J]. ASHRAE Transactions, 1984(90): 398-415.
[4] PASCAL S, DOMINIQUE M. Simplified model for indirect contact evaporative cooling-tower behavior[J]. Applied Energy, 2004, 78(4): 433-451. DOI: 10.1016/j.apenergy.2003.09.004.
[5] BORIS H. A general mathematical model of evaporative cooling devices[J]. Revue Generale de Thermique, 1998, 37(4): 245-255. DOI: 10.1016/S0035-3159(98)80092-5.
[6] QURESHI B A, ZUBAIR S M. Second-law-based performance evaluation of cooling towers and evaporative heat exchangers[J]. International Journal of Thermal Sciences, 2007, 46(2): 188-198. DOI: 10.1016/j.ijthermalsci.2006.04.014.
[7] FOUDA A, MELIKYAN Z. A simplified model for analysis of heat and mass transfer in a direct evaporative cooler[J]. Applied Thermal Engineering, 2011, 30(5): 932-936. DOI: 10.1016/j.applthermaleng.2010.11.016.
[8] QURESHI B A, ZUBAIR S M. Prediction of evaporation loss in evaporative fluid coolers[J]. Applied Thermal Engineering, 2007, 27(2): 520-527. DOI: 10.1016/j.applthermaleng.2006.06.008.
[9] WU J M, HUANG X, ZHANG H. Numerical investigation on the heat and mass transfer in a direct evaporative cooler[J]. Applied Thermal Engineering, 2009, 29(1): 195-201. DOI: 10.1016/j.applthermaleng.2008.02.018.
[10] 张斌, 王北南. 转炉煤气干法除尘在国内的应用[J]. 中国科技信息, 2011(22): 114-114. DOI: 10.3969/j.issn.1001-8972.2011.22.067.
ZHANG B, WANG B N. Application of converter gas dry dedusting system in china[J]. China Science and Technology Information, 2011(22): 114-115. DOI: 10. 3969/j.issn.1001-8972.2011.22.067.
[11] 杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 2006: 13-237.
[12] 车得福, 李会雄. 多相流及其应用[M]. 西安: 西安通大学出版社, 2007: 64-80.

