利用阵列感应测井进行储层渗透率评价

周峰，孟庆鑫，胡祥云，Evert Slob，潘和平，马火林

1 中国地质大学(武汉)机械与电子信息学院，武汉 4300742 中国地质大学(武汉)地球物理与空间信息学院地球内部多尺度成像湖北省重点实验室，武汉 4300743 河北地质大学勘查技术与工程学院，石家庄 050031 4 代尔夫特理工大学土木与地球科学学院，荷兰 2628 CN

高明亮，于生宝，郑建波，徐畅，刘伟宇，栾卉*

吉林大学仪器科学与电气工程学院，长春 130026



利用阵列感应测井进行储层渗透率评价

周峰1,2，孟庆鑫3，胡祥云2*，Evert Slob4，潘和平2，马火林2

1 中国地质大学(武汉)机械与电子信息学院，武汉 4300742 中国地质大学(武汉)地球物理与空间信息学院地球内部多尺度成像湖北省重点实验室，武汉 4300743 河北地质大学勘查技术与工程学院，石家庄 050031 4 代尔夫特理工大学土木与地球科学学院，荷兰 2628 CN

钻井过程中储层受到泥浆侵入影响的程度与储层岩性有着密切关系，其中储层渗透率对侵入深度有着较大影响，因此若可以获知泥浆侵入深度，则有望对储层渗透率进行评估.本文首先建立含泥饼增长的泥浆侵入数值模型，然后建立阵列感应测井数值模型，两者的联合正演模拟显示泥浆侵入对地层的影响可以反映在阵列感应测井响应上，利用阻尼最小二乘法对阵列感应测井响应进行反演可以得到侵入深度.对侵入深度和储层渗透率的关系进行分析发现：在渗透率为1～100 mD(1 mD= 0.987×10-3μm2)数量级的储层中，渗透率的变化可以在侵入深度上得到反映.以储层和井数据进行二维数值模拟发现：利用阵列感应测井响应反演出来的侵入深度曲线反映了渗透率在地层上的变化趋势，采用解释图版的方法可以对储层各层段的渗透率进行粗略估算.

阵列感应测井；渗透率评价；泥浆侵入

1 引言

在石油钻井过程中，由于井底泥浆和储层之间存在着压力差，泥浆滤液渗入到储层孔隙中，改变了井壁附近的流体成分，影响了测井工具对地层参数的准确测量.因此，研究泥浆侵入对测井的影响并寻求有效的校正方法，对于储层测井评价具有重要的意义(刘尊年等，2012).张建华等(1994)对泥浆侵入过程进行了一维数值模拟，陈福煊和孙嘉戌(1996)建立了砂槽物理实验来研究泥浆侵入对地层电导率的影响，Dewan和Chenevert(2001)基于物理实验建立了泥饼动态增长的数学模型，李长喜等(2006)分析了泥浆侵入中的低阻环带的成因，常文会等(2010)在柱坐标下对泥浆侵入进行了二维数值模拟，Wu等(2004)和Deng等(2008)开展了斜井泥浆侵入数值模拟，Salazar和Torres-Verdín(2009)比较了水基和油基泥浆侵入对储层的影响.泥浆侵入对地层参数的影响在阵列感应测井上有着明显反映，仵杰等(2009)基于简化的活塞状侵入模型进行了感应测井的数值模拟；邓少贵等(2010)利用斜井泥浆侵入下的阵列侧向测井来反演原状地层电阻率；李虎等(2013)利用阵列感应测井和自然电位测井进行联合反演来校正泥浆侵入影响，计算地层水电阻率.

前人所做的工作主要是将泥浆侵入视为不利因素，从而寻求校正泥浆侵入的方法，以减少其对测井产生的不利影响.然而受泥浆侵入影响的测井响应也携带了有用的储层信息，比如泥浆侵入深度与储层渗透率或孔隙度及其他岩石物性参数有着密切关系.张海龙等(2005)建议利用泥浆对储层流体的冲刷程度来预测油气层产能，王建华等(2009)认为储层渗透率是影响钻井滤液侵入深度的关键参数之一.本文认为可以通过阵列感应测井反演出泥浆侵入深度，再将泥浆侵入深度和储层渗透率建立起关联，从而实现储层渗透率的半定量或者定量评价.

本文建立含泥饼动态增长的泥浆侵入数值模型，基于Born几何因子方法建立阵列感应测井数值模型，并利用阻尼最小二乘法来反演泥浆侵入深度；分析泥浆侵入深度和储层渗透率的关系，利用储层数据进行泥浆侵入和阵列感应测井的正反演，以验证借助于泥浆侵入效应的阵列感应测井反演可以对储层渗透率进行有效评估.

2 泥浆侵入模型

除了储层参数外，泥饼参数(如泥饼渗透率)对于侵入流速也有较大的影响(王建华等，2009)，因此要研究泥浆侵入和储层岩性参数的关系，必须考虑泥饼在侵入中的作用.目前国内的泥浆侵入模型一般都忽略了泥饼，或者将泥饼参数简单视为一个定值，这样得到的侵入剖面特征虽然和真实情况相符，但是侵入液量以及侵入深度却和真实情况偏差较大.为此将泥饼动态增长模型耦合到多相流多组分模型中，发展出一个更接近实际的泥浆侵入模型.

2.1 多相流多组分模型

以水基泥浆侵入为例，忽略气相的参与，假设侵入过程符合等温达西渗流，则近井区域中的孔隙压力和含水饱和度可由油水两相等温达西渗流方程求解(Aziz and Settari,1979)：

(1)

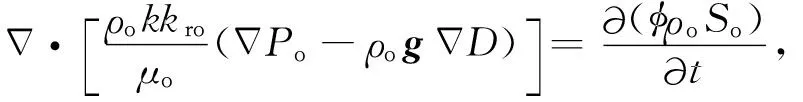
(2)

其中ρw和ρo分别为水和油的密度(kg·m-3)，k为储层渗透率(m2)，krw和kro分别为水和油的相对渗透率，g是重力加速度矢量(m·s-2)，D是储层深度(m)，μw和μo分别为水和油的黏度(Pa·s)，Pw和Po分别是水和油的压力(Pa)，φ为孔隙度，Sw和So分别为水和油的饱和度，t为侵入时间(s).

地层水与侵入的泥浆滤液水之间由于矿化度不同而发生盐分混溶，采用对流扩散方程求解水的矿化度(Navarro,2007)：

(3)

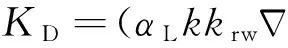
在柱坐标下对上述公式进行有限差分的离散，压力和矿化度采用隐式求解，饱和度采用显式求解，得到不同侵入时间的含水饱和度和地层水矿化度的径向分布，再通过阿尔奇公式得到地层的电阻率(Archie,1942)：

(4)

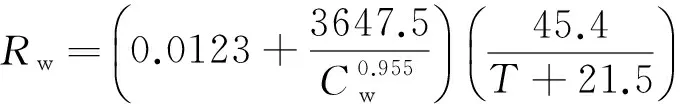
(5)

其中Rf和Rw分别为地层综合电阻率和地层水电阻率(Ωm)，m和n分别为胶结指数和饱和度指数，α为岩性导电附加系数，T是温度(℃).

2.2 泥饼动态模型

泥浆滤液中含有一定的固体颗粒成分，在侵入发生时泥浆中的泥质成分逐渐沉积在井壁上形成泥饼.泥饼参数对于侵入流速至关重要，泥饼的渗透率、孔隙度随时间的变化可以表示为(Wu et al.,2005)：

(6)

(7)

其中kmc和φmc分别为泥饼渗透率和孔隙度，Pmc为泥饼内外压差，kmc0和φmc0为泥饼参考渗透率和参考孔隙度，由1 psi压差下的实验测量值所确定，v和δ分别为压缩指数和相渗关系因子，均为实验室可测定值.该公式计算时，渗透率取mD为单位，压力以psi为单位，其他参数无量纲.

泥浆滤液瞬时侵入速率表示为(Wu et al.,2005)：

(8)

其中qmc为瞬时泥浆侵入速率(m3·s-1)，h为目标储层厚度(m)，Pm为泥浆压力(Pa)，μmc为泥浆黏度(Pa·s)，rw为井筒半径(m)，rmc为泥饼内径(m)，下标i为离散化后的网格序数，i=1表示泥饼网格，i=N表示模型外边界.水基泥浆侵入时只考虑附在井壁内侧的外泥饼的影响(Salazar and Torres-Verdín,2009；王建华等，2009)，因此有rw>rmc.该式子中分母的第一部分和第二部分因式分别代表地层和泥饼的流阻.泥饼厚度随侵入时间的增长值可以用(9)式求解(Wu et al.,2005)：

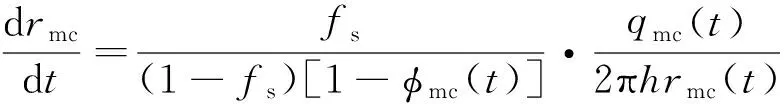
(9)

其中fs为泥浆中泥质成分的体积百分比含量.

求出每个时间步的泥饼渗透率、孔隙度和厚度，将其作为多相流模型中第一个网格变量，可以实现泥饼增长模型和多相流多组分模型的耦合.整个模拟区域在径向上采取非均匀网格，垂向采用均匀网格，内外边界均采取定压边界条件，利用MATLAB程序开发，得到一个完整的泥浆侵入数值模拟器.

2.3 模型验证

Salazar和Torres-Verdín(2009)基于商用的多相流多组分模拟软件CMG-STAR进行二次开发，实现含泥饼动态增长的泥浆侵入数值模拟.下面将本文自主开发的泥浆侵入数值模拟程序与Salazar和 Torres-Verdín(2009)的模型在相同参数设置下进行计算对比，以验证本模型的有效性.基本的储层和流体参数如表1所示，分别对渗透率为10、30、100 mD的储层进行侵入100 h的模拟.对比发现：用本模拟器得到的侵入流速和泥饼厚度随着时间的变化曲线(图1a，1b)和文献(Salazar and Torres-Verdín,2009)中对应的曲线(图2a，2b)基本吻合，证实了本文自主开发的数值模拟程序的准确性.

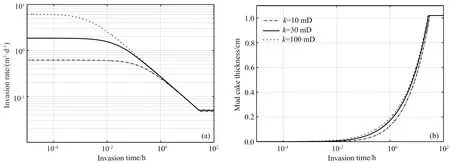
图1 本文中的数值模拟程序得出的侵入流速(a)和泥饼厚度(b)随时间的变化曲线Fig.1 Invasion rate (a) and mud cake thickness (b) versus time by the autonomous program

图2 发表文献中的侵入流速(a)和泥饼厚度(b)随时间的变化曲线(Salazar and Torres-Verdín,2009)Fig.2 Invasion rate (a) and mud cake thickness (b) versus time in the publication (Salazar and Torres-Verdín,2009)

参数值单位井径0.1454m储层厚度1m储层外径610m径向网格数51储层初始压力25166kPa井底压力27580kPa束缚水饱和度8%残余油饱和度10%地层水矿化度160×103mg/L泥浆矿化度3×103mg/L地层初始含水饱和度30%地层孔隙度25%泥饼参考渗透率0.03mD泥饼参考孔隙度25%泥饼最大厚度1.02×10-2m参数值单位泥饼压缩指数0.4泥饼乘积因子0.1泥浆固态体积含量6%地层温度100.6℃水相相对渗透率经验指数3油相相对渗透率经验指数3水相相对渗透率端点值30%油相相对渗透率端点值100%孔隙分布经验指数15毛细压力系数2.74×10-2Pa·m径向弥散度0m胶结指数2饱和度指数2岩性导电附加系数1

3 阵列感应测井正反演

以哈利伯顿高分辨率阵列感应测井仪(HRAI)为参考，线圈系装置提供探测深度分别为10 in、20 in、30 in、60 in、90 in(1 in=25.4 mm)的视电阻率曲线.考虑到小极距线圈系装置反映的是浅层信号并主要用于校准分辨率，因此在反演中舍弃了10 in探测深度的视电阻率曲线.

3.1 正演模型

本研究中阵列感应测井正演基于几何因子原理.该原理可直观快速地模拟感应测井响应，并发展出适用于不同地电模型的修正几何因子，其中Born几何因子可描述非均匀地层中电导率在背景上的扰动，适用于泥浆侵入地层，其视电导率算式可写为(王卫等，2011)：

(10)

gBorn(r,z)=gDoll(1-ikrT)(1-ikrR)eikrR+ikrT，

(11)

其中σa为双线圈系所得视电导率(S·m-1)，根据不同极距装置组合可得各子阵列结果；gBorn(r,z)表示位于垂向z和径向r处的单元环的Born几何因子，gDoll为Doll几何因子，k为复波数，rT、rR分别为发射线圈和接收线圈到单元环的距离(m)，i表示虚部；σ(r,z)为垂向z和径向深度r处的单元环电导率(S·m-1).根据径向分层模型可进一步写出总式：

(12)

其中σt为原状地层电导率(S·m-1)，σi为侵入带电导率(S·m-1)，σm为井眼泥浆电导率(S·m-1).Gm、Gi、Gt为积分几何因子，是由几何因子理论得到的不同地层区域对测井响应的贡献值.计算上述式子，可得各阵列感应测井系的视电导率(取倒数即得视电阻率).

3.2 反演方法

基于上述正演算法，应用N个测井数据观测值求取具有w个参数的正演模型来完成拟合反演，该过程的数学表达式写为(李虎等，2013)：

dn=Fn(p1,p2,p3,…,pw),(n=1,2,…,N)

(13)

其中dn表示测井观测数据，Fn表示正演模型，pw表示待反演的w个模型参数.采用阻尼最小二乘法求解，目标函数可写为：

(14)

其中P=(p1,p2,p3,…,pw)T，表示待反演参数的转置矩阵，P为极小解的必要条件需满足O(P)在P处的梯度为零.将非线性函数F(P)在初始近似值P(0)处做泰勒展开，并略去二次项及二次以上项进行近似表示，目标函数的矩阵形式可写为：

F[ΔP(0)]=[J0ΔP(0)-ε0]T[J0ΔP(0)-ε0]，

(15)

其中J0为初始刚度阵，ε0为初始残量.

若反演刚度阵J是满秩，则由式JTJΔP=JTε可知，F(P)极小点的进一步近似P(1)由(16)式确定：

(16)

(17)

式中P(k)为第k步迭代解，Jk为第k步反演刚度阵(Jacobi阵)，λk为阻尼因子，εk为每步残量.

当泥浆侵入是典型的低阻侵入时，冲洗带和低阻环带差别不明显，可将其一起视为侵入带作为一个整体来讨论，故以三参数(侵入半径、侵入层电阻率、原状地层电阻率)进行反演.

3.3 方法验证

将本研究中的阵列感应正反演方法在一个典型的低阻侵入储层中进行验证，含水饱和度、地层水矿化度和地层电阻率的径向剖面如图3所示.可以看出，每隔24 h侵入前缘距离井壁的距离分别为0.50 m、0.75 m、0.95 m和1.1 m(图3a)，由于侵入液量以环柱状展开，因此侵入深度的增加值是逐渐减缓的.地层水矿化度随时间的变化趋势与含水饱和度基本一致，但略滞后于含水饱和度的变化(图3b)，分析认为主要是由于盐分的分子混溶效应引起.由图3c可以看出：地层电阻率在井壁附近存在一个10～15 Ωm的低阻区域，呈现出低侵的特征，对应于泥浆冲洗带；最外侧47 Ωm为原状地层电阻率；在冲洗带与原状地层之间存在5～10 Ωm的低阻环带.低阻环带主要是由于矿化度变化滞后于含水饱和度引起，低阻环带和原状地层之间的分界面对应于含水饱和度前缘，而低阻环带与冲洗带之间的分界面则对应于矿化度前缘，因此若在电测井中显示出两个电阻率突变的响应特征，则第二个突变对应于实际侵入前缘，这种影响在高阻侵入时应尤为注意.在低阻侵入的时候，低阻环带和冲洗带之间的电性差别不十分明显，因此在阵列感应反演中可将低阻环带和冲洗带作为一个整体来考虑，只寻找侵入带和原状地层的分界面，进而获取侵入深度.

采用阵列感应测井数值模型对上述地电模型进行正演模拟，得到的阵列感应响应如图4所示.可以看出：受低阻侵入的影响，侵入剖面上的视电阻率曲线偏小，分析原因是由于侵入带电阻率较小，邻近收发装置增大了其信号贡献率；随着侵入半径的增加，各子阵列视电阻率值逐渐降低，特别是深部径向视电阻率值(R60和R90)的降低幅度较大，同时各子阵列感应曲线受到逐步增大的低阻侵入带的影响，分异性降低(视电阻率值趋向于低阻).阵列感应测井响应的变化能够反映出泥浆侵入深度随着时间的增加.

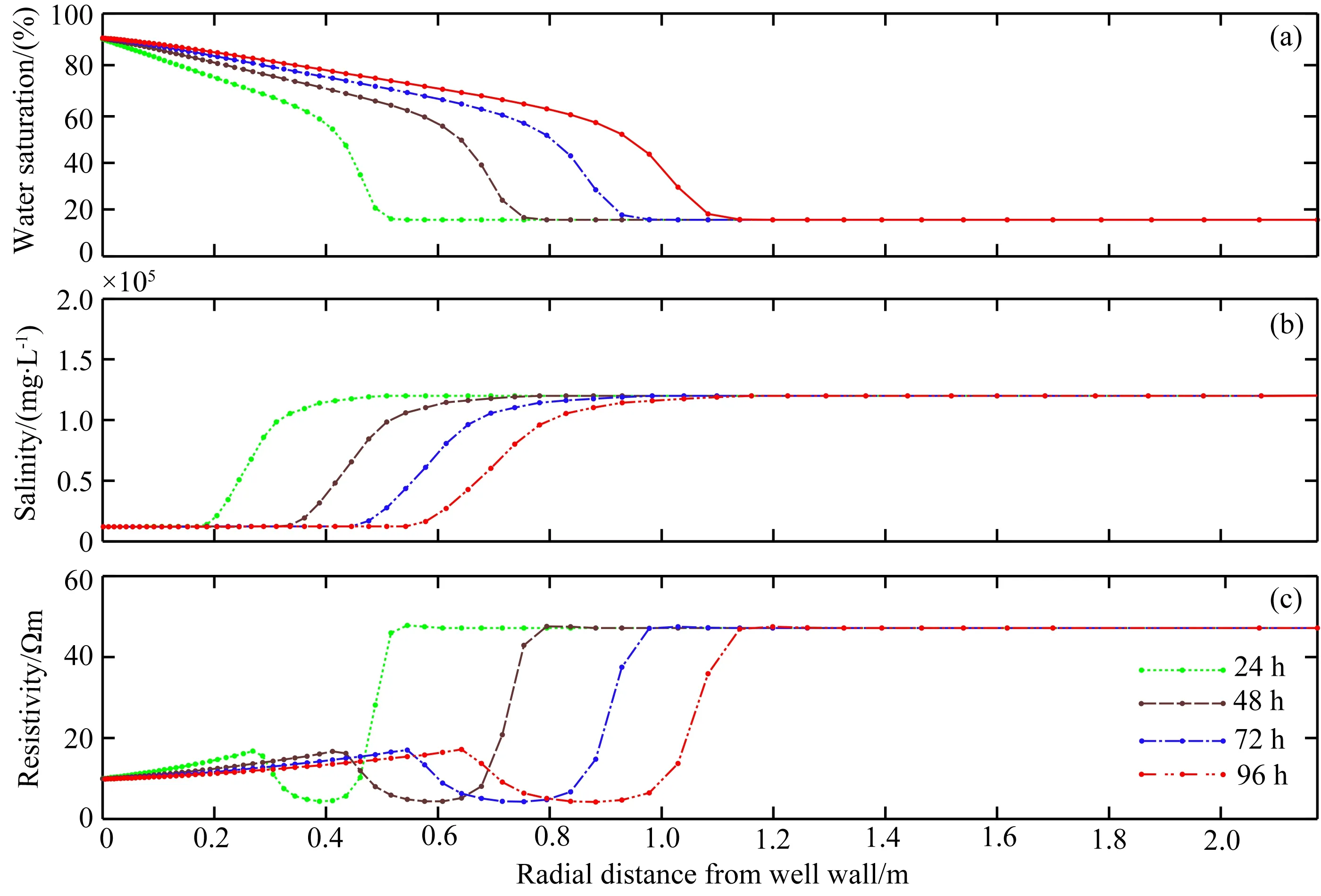
图3 含水饱和度(a)、地层水矿化度(b)和综合电阻率(c)的径向分布Fig.3 Radial distributions of water saturation (a),water salinity (b),and comprehensive resistivity (c)

图4 侵入24 h间隔对应的阵列感应测井视电阻率Fig.4 Apparent resistivities of array induction logging every 24 hours of invasion

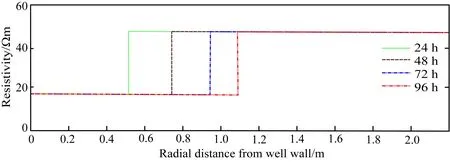
图5 反演得到的侵入带电阻率、原状地层电阻率和侵入深度Fig.5 Invasion zone resistivity,virgin zone resistivity,and invasion depth inversed from apparent resistivity

基于上述阵列感应测井响应进行三参数反演，得到侵入带电阻率、原状地层电阻率和侵入深度的值如图5所示，与泥浆侵入数值模拟进行对比可以看出反演结果较为准确地反映出受侵入影响储层的电性结构(图3c)，对于本文所关心的侵入深度值而言，反演结果与数值模拟结果一致(图3a)，证实了该反演方法的有效性.

4 渗透率评价应用

前人进行阵列感应测井反演时，往往只关注如何校正出原状地层的真电阻率，而未对侵入深度进行利用.上面方法反演出泥浆侵入深度，其潜在的应用是进行储层渗透率评价.

4.1 渗透率与侵入深度关系

实际钻井过程中，钻头以较高的剪切速度钻开地层，泥浆滤液以较大的速率渗入地层，此时虽然有部分固体颗粒沉积在井壁上，但由于泥浆随钻头在井内高速旋动，使得泥饼厚度小、渗透率大，故泥饼对侵入的阻碍作用不大.起钻后，井下液体呈现静滤失状态，大量泥浆固体颗粒沉积在井壁上，泥饼厚度增加，在内外静压差作用下泥饼渗透率变小，泥饼流阻加大，泥浆滤液的滤失速率降低(Peng and Peden,1992).基于上述2.3节算例的参数进行数值模拟，设钻井时间为12 h，钻井过程中泥饼厚度为0.1 mm，泥饼渗透率为0.1 mD，泥饼孔隙度为45% (Navarro,2007).起钻后，储层受静态泥浆浸泡，泥饼孔渗参数变化按照公式(6)和(7)计算.通过对泥浆侵入进行参数敏感性分析发现：随着储层渗透率增大，侵入流速也会增加，但是在相同的侵入液量下，孔隙度的增加会减少侵入深度(范宜仁等,2013).实际储层的渗透率和孔隙度彼此具有相关性，因此在进行敏感性分析时必须考虑两者的同时变化对侵入深度的影响.以文献(Salazar and Torres-Verdín,2009)给出的几种典型的岩石物性参数为参考，设置储层孔隙度分别是15%、20%、25%、28%、30%，对应的储层渗透率分别是3、10、30、100、300 mD，其他参数不变，进行侵入100 h的数值模拟.

图6a、6b分别记录了侵入流速和累计侵入液量随时间的变化曲线，可以看出：在钻井的12 h时间，由于泥饼流阻较小，泥浆滤液以较大的速率侵入到储层中，孔渗性较好的储层对应的侵入流速较大(图6a)，侵入总液量也较大(图6b)，此时储层渗透率是决定侵入流速和液量的主要因素.随着钻井完成，井下泥浆呈现静滤失的状态，泥饼逐渐变厚且渗透率降低，侵入流速逐渐降至最小，且在不同孔渗性储层中侵入流速差别不大(图6a)，随着侵入时间的增加侵入总液量不再呈现明显增长(图6b)，分析认为主要原因是静滤失过程中泥饼渗透性小且厚度大，使得泥饼对侵入过程的影响显著，储层本身的渗透率不再是主要敏感性参数，这种趋势在高渗透率储层中特别明显.

鉴于钻井结束后侵入液量变化不大，因此提取侵入24 h时不同孔渗性储层的侵入剖面进行分析(图7a)，得到储层渗透率和侵入深度的关系如图7b所示.对比可以看出：随着储层渗透率增加，侵入深度逐渐增加，但是两者的关系呈现幂指数的递增关系，即储层渗透率增大，侵入深度相应增加，但是其增加幅度越来越小.分析原因认为：一方面储层渗透率越大，泥饼上的压降越大，储层内部压力梯度越小(图8)，因此储层渗透率变化对侵入流速的影响越小；另一方面，储层渗透率越大，储层对应的孔隙度越大，侵入液量虽然越大，但是由此带来的侵入深度的增加值却被孔隙度抵消了一部分.由此也可以推断，在高渗透率储层(103mD的量级以上)，随着储层渗透率的增加，侵入深度不再明显增加.

以上分析可以看出：储层渗透率在一定的范围内(1 mD至100 mD数量级)可以由侵入深度所反映.在小于1 mD的储层中，达西渗流理论受限，因此这里不做讨论.

4.2 半定量预测

以华北某油田测井和取心数据为例进行泥浆侵入的数值模拟.取深度从1036 m到1096 m的井段数据，井眼直径为0.2 m，钻井液矿化度为12000 mg/L，泥浆密度1130 kg·m-3，水和油的黏度分别为0.968 Pa·s和2.99 Pa·s，储层和泥浆压差为2 MPa，重力加速度为9.8 m·s-2，渗透率和孔隙度变化分别如图9a、9b所示，这里的渗透率为水平渗透率，垂向渗透率为水平渗透率的1/10.

以该井段的数据进行泥浆侵入二维数值模拟，得到侵入24 h后的含水饱和度剖面(图10a)和电阻率剖面(图10b).

将阵列感应测井响应进行逐层反演，得到侵入深度曲线如图11所示.比较侵入深度(图11红线)和储层渗透率(图11蓝线)，可以看出反演出来的侵入深度和储层渗透率在纵向上的变化趋势基本一致，尤其是侵入深度曲线变化明显反映出了渗透率曲线中两个极低和一个极高的特征.

图6 不同孔渗性储层对应的侵入流速(a)和侵入液量(b)随时间的变化Fig.6 Invasion rate and volume vs time for different porosity and permeability

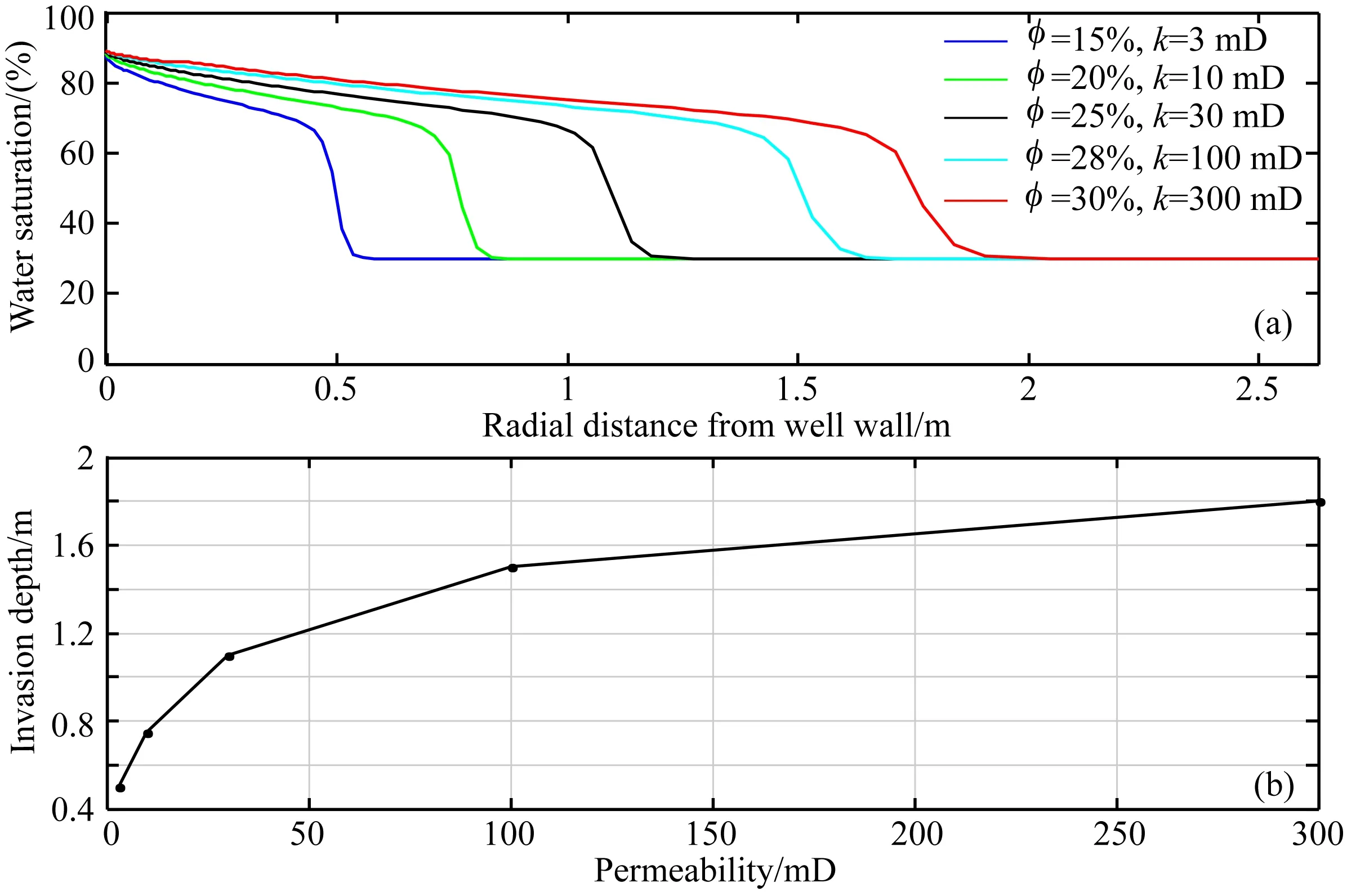
图7 侵入24 h含水饱和度径向分布(a)和储层渗透率与侵入深度关系曲线(b)Fig.7 Radial distributions of water saturation (a),and invasion depths vs reservoir permeabilities (b) after 24 hours of invasion

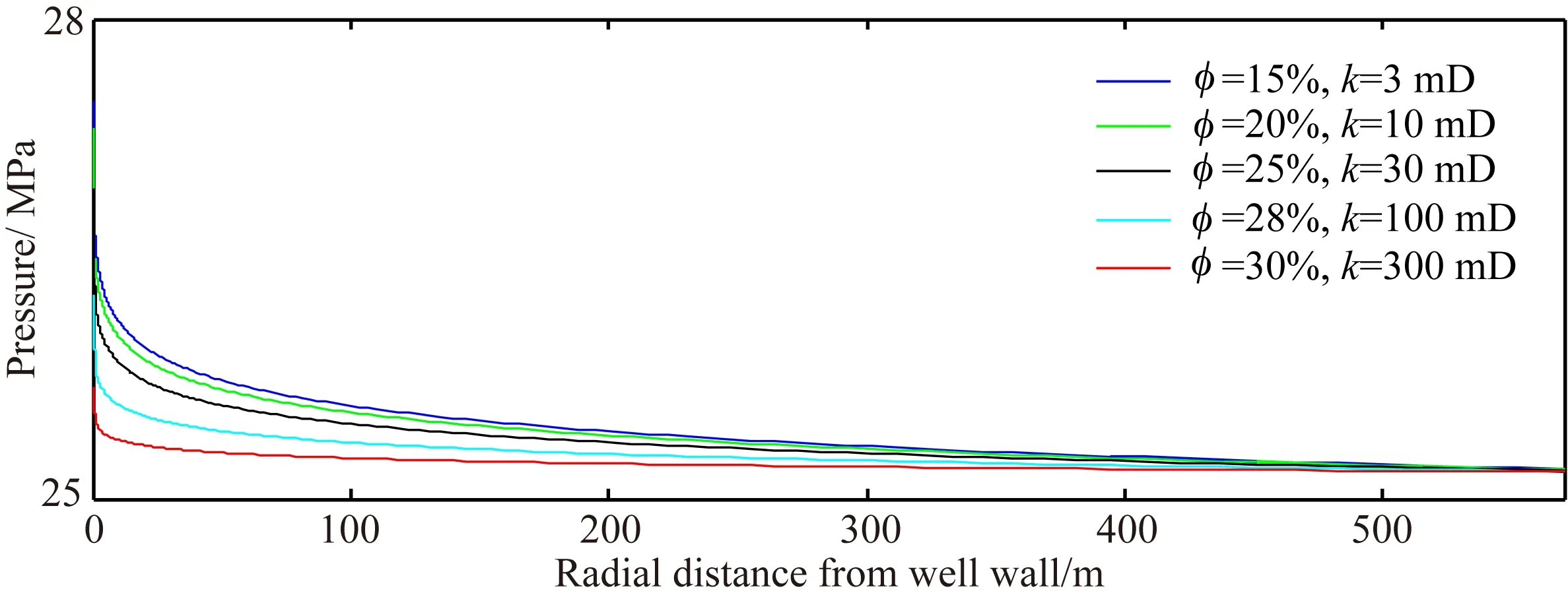
图8 侵入24 h时不同孔渗性储层对应的压力径向分布Fig.8 Radial distributions of formation pressure after 24 hours of invasion

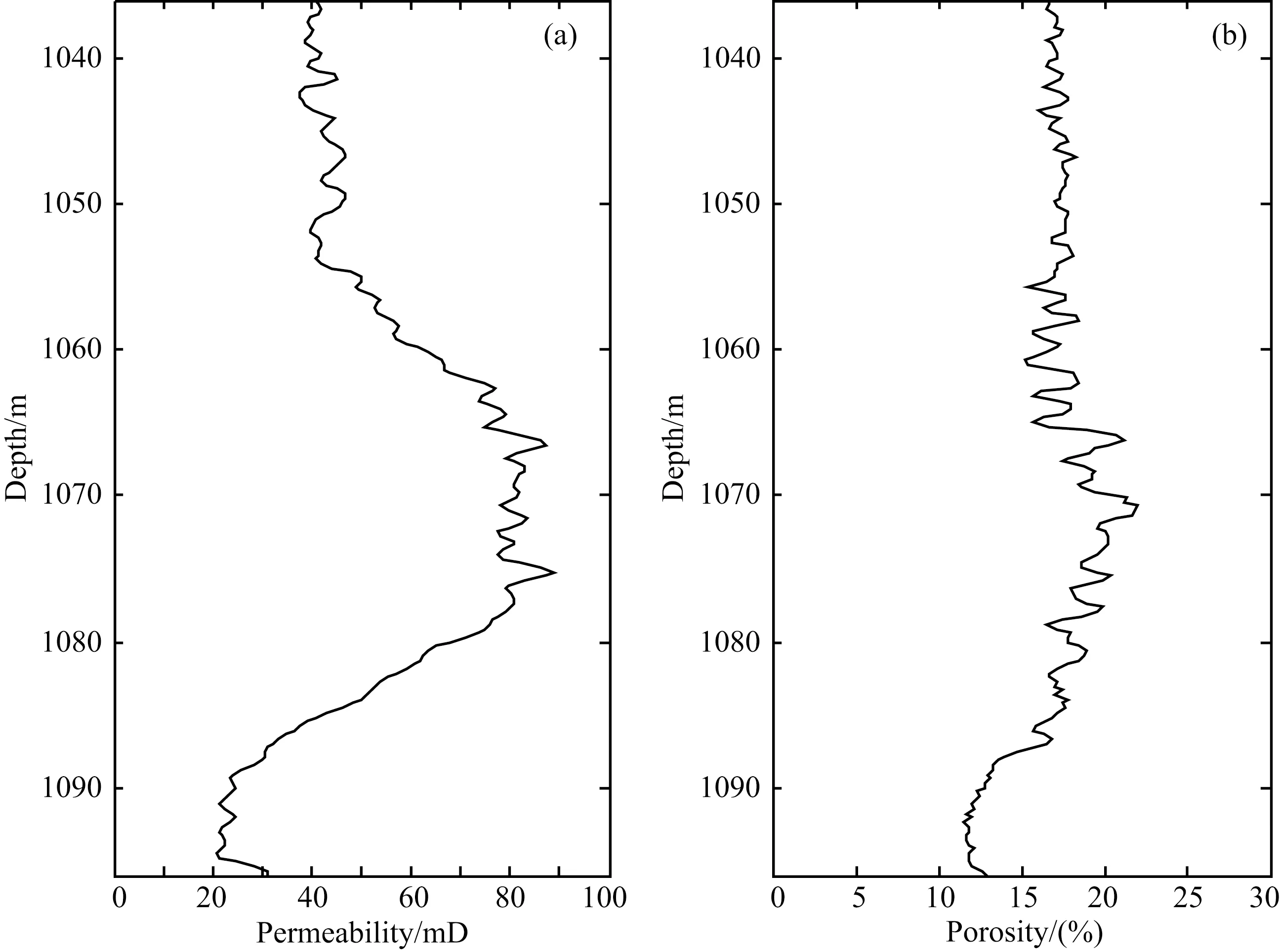
图9 华北某井段的渗透率(a)和孔隙度(b)曲线Fig.9 Permeability (a) and porosity (b) curves of an oil well in North China

图10 侵入24 h的含水饱和度(a)和电阻率(b)剖面Fig.10 Profiles of water saturation (a) and resistivity (b) after 24 hours of invasion

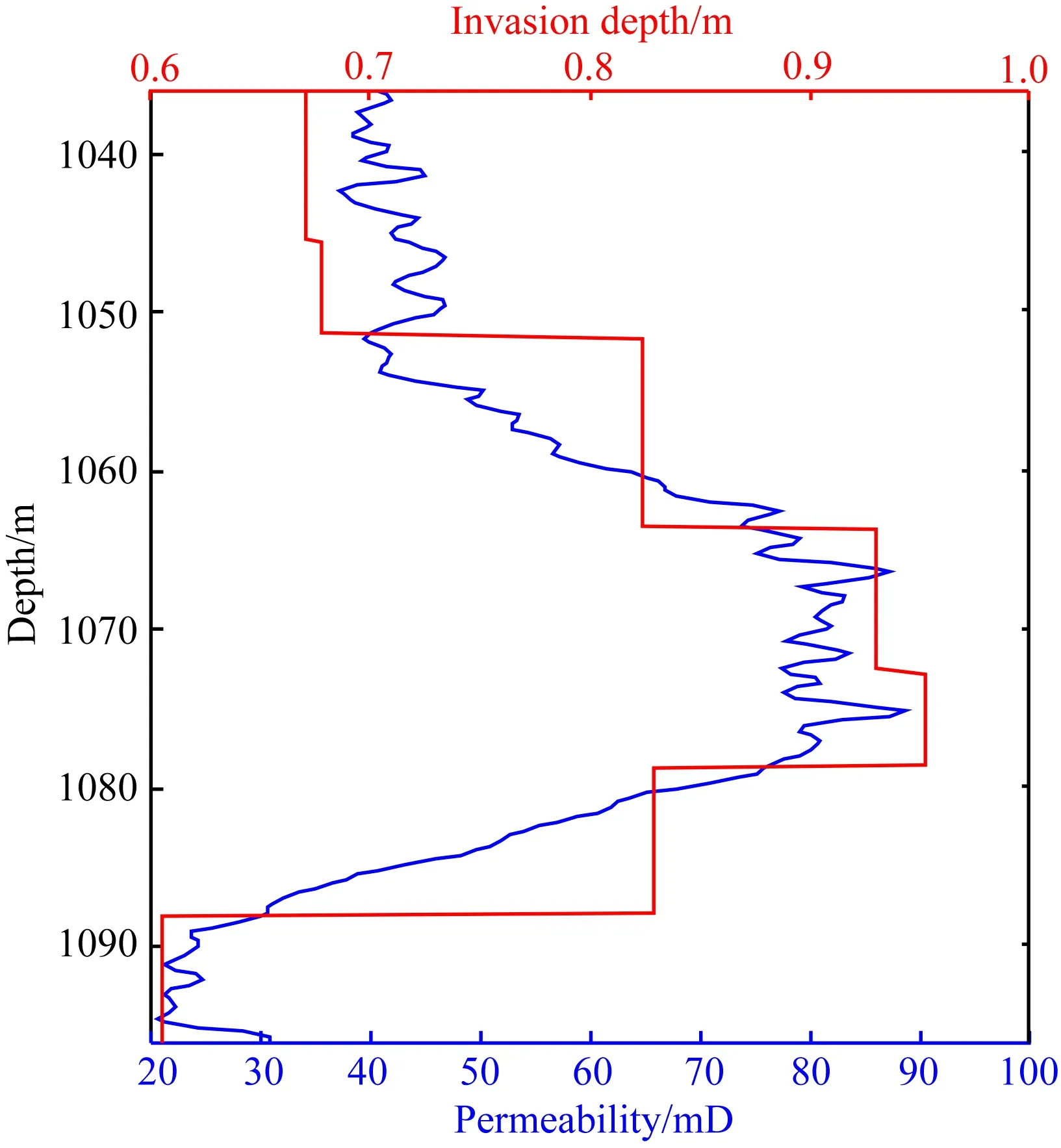
图11 反演的侵入深度(红色)和储层渗透率(蓝色)对比Fig.11 Contrast between the curves of invasion depth (red) and permeability (blue)

图12 二维轴对称的分层地层模型Fig.12 Two-dimensional axisymmetric layered form ation model

图13 侵入24 h的含水饱和度分布Fig.13 Water saturation distribution after 24 hours of invasion

图14 反演的侵入深度曲线Fig.14 Inversed invasion depth curve

4.3 图版定量评估

关于泥浆侵入的参数敏感性分析认为：储层的渗透率、孔隙度和含水饱和度是对侵入深度影响较大的地层参数，这几个参数也是在同一口井中随着深度变化较大的(Zhou et al.,2015).在实际生产中可以制作一系列解释图版集，建立起不同孔隙度、渗透率和含水饱和度对应的侵入深度值曲线，这样就可以利用获取的侵入深度及其他可测定参数值来粗略评估未知的储层渗透率.

在进行评估之前，将测井、钻井、取心中可以获知的基本参数代入到泥浆侵入数值模型中，并设置不同的孔隙度、渗透率和含水饱和度值进行一系列数值模拟，从而得到不同“孔-渗-饱”参数对应的侵入深度值，制作成侵入深度图版集.在现场测量时，孔隙度和含水饱和度通过常规测井获取后找到其对应的图版曲线，再利用阵列感应测井数据反演出侵入深度值，最后找到相应曲线中该侵入深度值所对应的储层渗透率值.

以上述井数据为基础，将地层“孔-渗-饱”随地层深度的变化简化为一个概念化的层状模型(图12)，其中孔隙度和含水饱和度是常规测井方法可测的，忽略了重力和垂向渗透率影响，数值模拟泥浆侵入24 h后的径向侵入剖面如图13所示.对阵列感应测井响应进行反演，计算得到各层的侵入深度分别为：0.37 m、0.78 m和1.07 m，如图14所示.

基于这口井的数据制作了一组反映侵入深度和渗透率关系的图版集，这里挑选出含水饱和度为20%、30%和40%的图版，如图15a—15c所示.针对第一层地层，找到在含水饱和度为20%的图版中孔隙度为10%的曲线，由侵入深度为0.37 m的横坐标找到纵坐标对应的值，即为估算的储层渗透率(如图中虚线所示).同理可以得到其他两个地层的渗透率估算值.表2的对比看出：估算的渗透率和预设的渗透率误差在一个数量级内，从储层评估的尺度上来说误差在可以接受的范围.误差来源一方面是阵列感应测井低的径向空间分辨率，另一方面是渐变而非活塞状的侵入前缘.可见使用解释图版可以粗略地估算出储层各个层段的渗透率，然而这种方法的缺点是需要预先进行大量的数值模拟计算来获取足够多的参数图版，以对应实际储层参数较大的取值范围.

表2 渗透率估算值和预设值(单位：mD)

5 结论

本文建立了一个含泥饼增长的泥浆侵入数值模型，基于Born几何因子方法建立了阵列感应测井数值模型，基于阻尼最小二乘法对阵列感应测井响应进行反演得到泥浆侵入深度值；分析了储层渗透率对侵入深度的影响，并利用阵列感应测井对储层渗透率进行评估.得出结论如下：在渗透率为1 ～100 mD数量级的储层中，泥浆侵入深度与储层渗透率有着较好的对应关系，利用阵列感应测井反演出的侵入深度值可以反映出储层渗透率的变化趋势，基于此方法建立的解释图版集可以在现场生产中用来粗略估算储层渗透率.

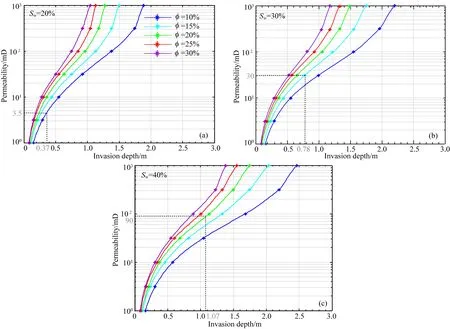
图15 含水饱和度为20%(a)、30%(b)和40%(c)时的渗透率解释图版Fig.15 Interpretation charts for water saturations of 20% (a),30% (b) and 40% (c)

尽管目前还没有一个理想的数学模型将泥浆侵入深度和储层渗透率之间的相关性进行直接和准确的量化，但是本文的研究为利用阵列感应测井进行渗透率定量评估提供可行性论证，也为将来借助阵列感应测井数据对储层渗透率进行直接准确的反演提供理论依据.

Archie G E.1942.The electrical resistivity log as an aid in determining some reservoir characteristics.Transactions of the American Institute of Mining,Metallurgical and Petroleum Engineering,146(1):54-62,doi:10.2118/942054-G.

Aziz K,Settari A.1979.Petroleum Reservoir Simulation.London:Applied Science Publishers.

Chang H W,Pan H P,Zhou F.2010.Two-dimensional numerical simulation of mud Invasion.Earth Science-Journal of China University of Geosciences (in Chinese),35(4):674-680,doi:10.3799/dqkx.2010.082.

Chen F X,Sun J X.1996.Simulation test of radial electric conductivity during the mud filtrate invading porous formation.Chinese Journal of Geophysics (Acta Geophysica Sinica) (in Chinese),39(S1):371-378.

Deng S G,Fan Y R,Li G X,et al.2008.Numerical simulation of mud invasion in deviated wells in curvilinear coordinates.∥2nd IASME/WSEAS International Conference on Geology and Seismology.Cambridge,UK,140-148.

Deng S G,Li Z Q,Fan Y R,et al.2010.Numerical simulation of mud invasion and its array laterolog response in deviated wells.Chinese Journal of Geophysics (in Chinese),53(4):994-1000,doi:10.3969/j.issn.0001-5733.2010.04.024.

Dewan J T,Chenevert M E.2001.A model for filtration of water-base mud during drilling:determination of mudcake parameters.Petrophysics,42(3):237-250.

Fan Y R,Hu Y Y,Li H,et al.2013.Numerical simulation of mud-cake dynamic formation and reservoir mud filtrate invasion.Well Logging Technology (in Chinese),37(5):466-471,doi:10.3969/j.issn.1004-1338.2013.05.002.

Li C X,Ouyang J,Zhou C C,et al.2006.Forming mechanism and application of low resistivity annulus in oil reservoirs invaded by fresh drilling mud.Petroleum Exploration and Development (in Chinese),32(6):82-86,doi:10.3321/j.issn:1000-0747.2005.06.020.

Li H,Fan Y R,Hu Y Y,et al.2013.Joint inversion of HDIL and SP with a five-parameter model for estimation of connate water resistivity.Chinese Journal of Geophysics (in Chinese),56(2):688-695,doi:10.6038/cjg20130233.

Liu Z N,Sun J M,Chi X R,et al.2012.Analysis of research present situation of mud invasion.Progress in Geophysics (in Chinese),27(6):2594-2601,doi:10.6038/j.issn.1004-2903.2012.06.037.

Navarro D.2007.Effects of invasion transient on resistivity time-lapsed logging [Master′s thesis].Houston:Houston University.

Peng S J,Peden J M.1992.Prediction of filtration under dynamic conditions.∥SPE International Symposium on Formation Damage Control.Lafayette,Louisiana:SPE:503-511,doi:10.2118/23824-MS.

Salazar J M,Torres-Verdín C.2009.Quantitative comparison of processes of oil-and water-based mud-filtrate invasion and corresponding effects on borehole resistivity measurements.Geophysics,74(1):E57-E73,doi:10.1190/1.3033214.

Wang J H,Yan J N,Zheng M.2009.Prediction model for invasion radius of solids and filtrate in drilling fluids.Acta Petrolei Sinica (in Chinese),30(6):923-926,doi:10.7623/syxb200906023.

Wang W,Liao D L,Wu J.2011.Inversion of array induction based on Born geometric factor.Journal of Oil and Gas Technology (in Chinese),33(8):82-85，doi：10.3969/j.issn.1000-9752.2011.08.018.

Wu J H,Torres-Verdin C,Sepehrnoori K,et al.2004.Numerical simulation of mud-filtrate invasion in deviated wells.SPE Reservoir Evaluation &Engineering,7(2):143-154,doi:10.2118/87919-PA.

Wu J H,Torres-Verdín C,Sepehrnoori K,et al.2005.The influence of water-base mud properties and petrophysical parameters on mudcake growth,filtrate invasion,and formation pressure.Petrophysics,46(1):14-32.

Wu J,Feng J,Xie X C,et al.2009.Forward analysis of high definition induction logging response in mud invasion formation.Well Logging Technology (in Chinese),33(3):212-217,doi:10.3969/j.issn.1004-1338.2009.03.004.

Zhang H L,Liu G Q,Zhou C C,et al.2005.Reservoir productivity prediction by array induction logging data.Petroleum Exploration and Development (in Chinese),32(3):84-87,doi:10.3321/j.issn:1000-0747.2005.03.021.

Zhang J H,Hu Q,Liu Z H.1994.A theoretical model for mud-filtrate invasion in reservoir formations during drilling.Acta Petrolei Sinica (in Chinese),15(4):73-78,doi:10.7623/syxb199404010.

Zhou F,Hu X Y,Meng Q X,et al.2015.Model and method of permeability evaluation based on mud invasion effects.Applied Geophysics,12(4):482-492,doi:10.1007/s11770-015-0513-1.

附中文参考文献

常文会,潘和平,周峰.2010.泥浆侵入二维数值模拟.地球科学:中国地质大学学报,35(4):674-680,doi:10.3799/dqkx.2010.082.

陈福煊,孙嘉戌.1996.泥浆滤液侵入孔隙地层径向导电特性的模拟实验.地球物理学报,39(S1):371-378.

邓少贵,李智强,范宜仁等.2010.斜井泥浆侵入仿真及其阵列侧向测井响应数值模拟.地球物理学报,53(4):994-1000,doi:10.3969/j.issn.0001-5733.2010.04.024.

范宜仁,胡云云,李虎等.2013.泥饼动态生长与泥浆侵入模拟研究.测井技术,37(5):466-471,doi:10.3969/j.issn.1004-1338.2013.05.002.

李长喜,欧阳健,周灿灿等.2006.淡水钻井液侵入油层形成低电阻率环带的综合研究与应用分析.石油勘探与开发,32(6):82-86,doi:10.3321/j.issn:1000-0747.2005.06.020.

李虎,范宜仁,胡云云等.2013.基于阵列感应与自然电位联合反演地层水电阻率.地球物理学报,56(2):688-695,doi:10.6038/cjg20130233.

刘尊年,孙建孟,迟秀荣等.2012.泥浆侵入研究现状分析.地球物理学进展,27(6):2594-2601,doi:10.6038/j.issn.1004-2903.2012.06.037.王建华,鄢捷年,郑曼.2009.钻井液固相和滤液侵入储层深度的预测模型.石油学报,30(6):923-926,doi:10.7623/syxb200906023.王卫，廖东良，仵杰.2011.基于Born几何因子的阵列感应反演研究.石油天然气学报，33(8):82-85，doi：10.3969/j.issn.1000-9752.2011.08.018.

仵杰,冯娟,解茜草等.2009.泥浆侵入地层中高分辨率感应测井响应特征的正演分析.测井技术,33(3):212-217,doi:10.3969/j.issn.1004-1338.2009.03.004.

张海龙,刘国强,周灿灿等.2005.基于阵列感应测井资料的油气层产能预测.石油勘探与开发,32(3):84-87,doi:10.3321/j.issn:1000-0747.2005.03.021.

张建华,胡启,刘振华.1994.钻井泥浆滤液侵入储集层的理论计算模型.石油学报,15(4):73-78,doi:10.7623/syxb199404010.

(本文编辑 何燕)

高明亮，于生宝，郑建波等.2016.基于IGA算法的电阻率神经网络反演成像研究.地球物理学报，59(11):4372-4382,doi:10.6038/cjg20161136.

Gao M L，Yu S B，Zheng J B，et al.2016.Research of resistivity imaging using neural network based on immune genetic algorithm.Chinese J.Geophys.(in Chinese),59(11):4372-4382,doi:10.6038/cjg20161136.

高明亮，于生宝，郑建波，徐畅，刘伟宇，栾卉*

吉林大学仪器科学与电气工程学院，长春 130026

摘要 为满足地球物理资料反演解释的高精度、快速、稳定的要求，本文结合免疫遗传算法寻优速度快和BP神经网络反演不依赖初始模型等优点，设计了一种将BP神经网络和免疫遗传算法进行有机结合的全局优化反演策略，并将该策略成功地应用于二维高密度电法数据反演.利用免疫遗传算法(Immune Genetic Algorithm，简称IGA)对神经网络的反演参数进行同步优化，提高了电阻率反演的精度.仿真和实验结果验证设计的全局优化反演策略取得了较好的效果，通过与线性反演方法和BP法以及遗传神经网络法等反演方法进行比较，得出该方法具有反演精度更高，反演时间更短等显著优势的结论.

关键词 免疫遗传算法；BP神经网络；高密度电阻率法；反演精度

基金项目 地面电磁探测(SEP)系统研制-野外试验研究(201311193-05(SinoProbe-09-02-05))资助

作者简介 高明亮，男，1987年生，博士，研究方向为直流电法非线性反演方法研究.E-mail：mlgao13@mails.jlu.edu.cn

*通讯作者 栾卉，女，1979年生，副教授，硕士生导师，研究方向为电磁勘探方法研究.E-mail：luanhui@jlu.edu.cn

Abstract In order to meet the requirements of high precision,high speed and stability in geophysical inversion,we design a global optimization inversion strategy based on BP neural network and immune genetic algorithm,considering the fast searching speed of immune genetic algorithm and the independence of the initial model in BP neural network inversion.The strategy is successfully applied to the two-dimensional high density resistivity inversion.By using Immune Genetic Algorithm (IGA) for synchronous optimization of the neural network inversion parameters,the precision of the resistivity inversion can be improved .The results of experiment and simulation verify that the global optimization strategy achieves great results.Comparing with the linear inversion method,BP method,and genetic neural network method,our method has higher precision and shorter time of inversion.

Keywords Immune Genetic Algorithm;BP neural network;High density resistivity method;Inversion precision

1 引言

随着计算机技术和最优化方法的发展，非线性反演方法在地球物理领域逐步显示出强大的生命力(徐海浪和吴小平，2006；刘斌，2010；张凌云，2011；戴前伟等，2014).近年来，国内外关于电阻率非线性反演方法进行了较深入的研究，取得了一些成果.目前非线性反演方法研究主要集中在一维、二维反演方面，其中神经网络算法以其较强的计算能力和学习能力在地球物理反演领域应用最为广泛(Poulton and El Fouly，1991；Calderon-Macis et al.，2000；Spichak et al.，2002；Fani et al.，2013).Jimmy(2004)、Singh(2005)等率先将神经网络算法引入电阻率测深的一维反演工作中.在2D、3D电阻率非线性反演中，采用神经网络法进行了电阻率反演研究，不依赖于初始模型，不需要求解偏导数矩阵且反演速度较快，取得了较好的反演效果(El-Qady and Keisuke，2001；Mann，2006；Ahmad and Samsudin，2009；Singh et al.，2010).但是由于神经网络的固有特性，存在网络结构不稳定，反演容易陷入局部极小、收敛慢等问题(Poulton et al.，1992；Cranganu et al.，2007；Vladimir and Krasnopolsky，2007).国内外学者对此进行了较为深入的研究，对神经网络算法做了进一步改进，通过蚁群算法、遗传算法等算法对网络进行优化(Dai et al.，2014；Marina et al.，2014)，克服了神经网络的上述缺点.Maiti等(2011)提出将蒙特卡罗法与神经网络相结合进行混合二维电阻率反演，张凌云和刘鸿福(2011)利用蚁群算法对神经网络的结构参数进行了优化，改善了神经网络容易陷入局部极小的问题，但是网络收敛速度慢，反演精度有待提高.通过对蚁群、模拟退火等多种非线性方法研究发现遗传算法与神经网络相结合进行混合反演，其反演精度最高(张凌云，2011).遗传算法属于随机优化算法，通过初始值的改变寻找最优解，而在网络维数较大的情况下，随机优化算法较组合排序算法具有更明显的优势.虽然遗传算法与神经网络混合反演的反演精度最高，但是遗传算法优化神经网络参数时间较长，遗传算法的解空间容易被相似性高的适应值个体充满而缺乏多样性，导致算法早熟，局部搜索能力变差(周明等，1999；单文桃等，2013).针对遗传算法的不足，本文尝试将免疫遗传算法与神经网络进行混合反演.通过在遗传算法中引入免疫算子并将BP算法嵌入其中，优化神经网络的反演参数.这种混合反演方法解决了单一遗传算法优化神经网络时间过长的问题，加快了遗传算法搜索速度，提高全局搜索能力，确保快速收敛于全局最优解.同时克服了BP神经网络容易陷入局部极小，容错能力差，网络结构不稳定等问题，减少了反演迭代次数，节约了运算时间，并且可以获得更好的电阻率反演结果，实现了快速、高精度反演.

2 电阻率二维免疫遗传算法与BP神经网络混合反演

由于直流电阻率的建模与模型参数优化直接影响反演成像质量，因此对反演模型中的视电阻率进行预处理建模显得尤为重要.为满足地球物理反演高精度、快速、稳定的要求，并且适应复杂地质勘查情况，提高反演成像的快速性和准确性，本文应用BP神经网络算法对直流电阻率数据进行建模，利用免疫遗传算法对神经网络参数进行同步优化，模型输入为X、Z位置和视电阻率值D矩阵，U为D归一化处理的数据，yd和ya分别是参考模型和实际模型输出的真实电阻率矩阵，参考模型空间可通过地质信息或广义线性反演结果给定模型参数的变化范围.E为参考模型输出与实际输出电阻率值的均方差矩阵，BP神经网络反演参数通过免疫遗传算法进行在线和离线优化获得，从而使直流电阻率模型的实际电阻率能够准确跟踪参考模型输出，也就是均方差值E趋近于0.参考模型和BP神经网络模型都需要用BP神经网络.其中，参考模型是用来训练BP神经网络的初始反演参数，它是以离线的方式通过有限差分法正演数值计算产生训练集进而训练BP神经网络从而得到初始的反演参数(戴前伟等，2014).而作为反演模型的BP网络，其作用则是用以控制被控对象的输出能够跟随参考模型的输出.

基于IGA算法的电阻率神经网络反演成像主要分为三部分：BP神经网络建模、IGA算法优化神经网络反演参数、神经网络反演成像.图1为IGA优化的神经网络反演成像模型系统结构图.

2.1 BP神经网络建模

BP神经网络拓扑结构如图2a所示.神经网络包括输入层、隐含层和输出层.其中，输入层神经元的数量等于输入变量的个数，输出层神经元的数量等于输出变量的个数，隐含层神经元的数量可以依据输入信息量的大小和复杂度作相应的改变.本文将X、Z位置和视电阻率作为神经网络的输入，以真实电阻率作为神经网络的输出，这样的数据类型最适合神经网络的训练和测试.具体讨论参见第3节.BP神经网络的主要思想就是通过样本集训练网络，使得神经网络的输出与期望输出的误差平方和达到最小.它是通过反复迭代使相对误差函数在斜率下降的方向上计算网络权阈值和偏差的变化而逐渐达到目标.每一次权值和偏差的变化都与网络误差的响应成正比，并以发射传播的方式传到每一层.

图1 IGA优化的反演成像模型系统结构图Fig.1 The system structure diagram of inversion imaging model

图2 神经网络结构示意图(a) 神经网络拓扑结构;(b) 神经网络算式.Fig.2 A neural network structure diagram(a) The neural network topology;(b) The expression of neural network.

BP神经网络具体的结构算式如图2b所示.其中神经网络的每一隐含层都需要用到激活函数，本文选择logsig函数，其函数表达式如式(1)所示：

(1)

输入层到隐含层单元J表达式如下：

(2)

其中xi是神经网络的输入变量，netj是隐含层第j个神经元的输出，wij是神经网络的连接权值，bj是单元j第j个神经元的阈值.

隐含层单元J到输出层aj表达式为

(3)

BP神经网络训练算法一般采用梯度下降法来计算神经网络权值，权值更新规则如下：

(4)

式中，ε为学习动量，η为学习率，t为训练次数.

BP神经网络的学习误差E为

(5)

最终BP神经网络通过不断地迭代直到误差函数E足够小，网络训练结束.式中P为样本总数，N为输出节点数，apj和dpj分别为第p个样本中输出层神经网络第j个神经元实际输出和期望输出值.

2.2 免疫遗传算法

免疫遗传算法就是将免疫理论(Immune Algorithm，IA)和基本遗传算法(Simple Genetic Algorithm，SGA)各自的优点结合起来的一个多学科相互交叉、渗透的优化算法.免疫遗传算法可以看作一种新型融合算法，罗小平(2002)在遗传算法中加入免疫算子，使遗传算法变成具有免疫功能的新算法，是一种改进的遗传算法，该算法既保留了遗传算法的搜索特性，又利用了免疫算法的多机制求解多目标函数最优解的自适应特性，在很大程度上避免了“早熟”，收敛于局部极值.

2.3 IGA算法优化神经网络反演参数

本文应用免疫遗传算法优化神经网络的反演参数.对神经网络反演参数进行优化设计时，应在保证神经网络结构稳定的前提下，力求加快网络收敛速度，以实现高精度反演.在优化设计时，本文使用的目标函数与约束函数均是高度非线性的，属于多目标优化问题，适合于免疫遗传算法的求解.

2.3.1 建立目标函数

对于神经网络的优化设计可建立多种目标函数，但通常多以目标最小为目标函数，本文设计的目标函数为

(6)

将公式(1)、(2)、(3)代入(6)可以得到：

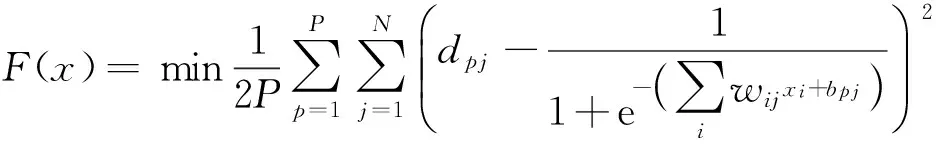
(7)

2.3.2 优化变量设计

式(7)为IGA优化的目标函数，其中目标函数内变量wij、bpj为免疫遗传算法优化的变量X.根据相关文献资料以及实验测试，本文确定选择有一个隐含层的三层IGA-BP神经网络进行训练.免疫遗传算法优化神经网络步骤如下：

(1) 编码

将待寻优变量X作为抗体.标准遗传算法一般采用二进制编码，其搜索能力强，交叉变异计算方便，但需要频繁的编码与解码，计算量较大而且精度不高.由于十进制编码精度更高，搜索空间更大，待优化参量较多，因而本研究采用十进制编码，可以减小搜索空间，有利于加快收敛速度.

(2) 初始抗体的生成

随机产生种群，为了避免无效抗体的产生，本文将变量的取值控制在规定范围内.

(3) 疫苗的提取

在免疫遗传算法中，疫苗是指从具体的待求解问题的先验知识中提取的一种特征信息.免疫遗传算法的运行效率和性能很大程度上取决于疫苗的合理选择.优良的疫苗对免疫算法的收敛速度有着决定性的影响.本文将每一代的最优解作为疫苗，动态地建立疫苗库，当前的最优解比疫苗库中的最差疫苗的亲和力高时，则取代该最差疫苗.

(4) 抗体产生(交叉与变异)

用设定的交叉概率Pc和变异概率Pm，按照标准遗传算法进行交叉和变异操作.

(5) 接种疫苗

从种群中选择要进行接种的个体，按照动态计算的接种率将疫苗的基因片段依次接入，即用疫苗基因置换抗体相应基因位上原有的基因，形成更好的免疫种群.

(6) 计算适应度和浓度

本文选择种群大小为100.运用IGA来搜索最优的函数参数X，计算抗体的适应度.公式(7)为本文参数寻优目标函数，而免疫遗传算法中的适应度函数通常为目标最大化问题，因此，适应度函数Fitness(x)为

(8)

(7) 免疫机制选择

免疫机制选择指每次遗传操作后，随机抽取一些个体注射疫苗，然后进行免疫检测.若亲和度提高，则继续；反之，说明在交叉、变异的过程中出现了严重的退化现象，这时该个体将被父代中对应的个体所取代.

(8) 终止条件的判断

免疫遗传算法在神经网络的优化过程中，本文定义终止条件为三种形式:

(a) 达到设定的循环迭代次数；

(b) 连续几代优化解没有改善；

(c) 达到最大优化时间.

满足其一，则将与抗原亲和度最高的抗体加入免疫记忆数据库中，输出最优结果并进行下一步.

(9) 获取神经网络参数

通过免疫遗传算法的深度优化，提供了一组最佳的网络参数，然后再进行神经网络反演，若满足反演效果，则进行下一步，否则，继续进行训练，直到达到满意结果.

(10) 仿真测试，结果输出.免疫遗传算法优化神经网络框图如图3所示.

3 二维IGA-BP电阻率反演成像建模

电阻率的反演建模是一个极其复杂的问题，Singh等(2010)使用采集的视电阻率和基单元作为网络模型的输入节点，真实的电阻率作为模型的输出节点，通过改变异常体的大小和位置作为网络训练样本，对于复杂的地质结构，则需要建立大量训练样本，耗费运算时间.徐海浪等(2006)考虑上述缺点，使用视电阻率作为网络模型的输入节点，真实电阻率作为网络模型的输出.但是由于输入和输出节点过大，导致网络收敛速度降低，训练和测试需要大量的时间.针对这个问题，戴前伟等(2014)提出了新的建模方式，将采集并预处理后的视电阻率数据按分布区域分组，以每个分组数据为神经网络的一个训练样本.虽然通过分割样本的大小来控制输入输出节点的数量，提高了网络收敛的速度并且节约了运算时间，但是依然存在输入输出节点过多的问题.Ahmand等(2010)使用采集的视电阻率和相应的水平、垂直位置作为网络模型的输入节点，相应位置的真实电阻率作为输出节点，其特点是输入输出节点少，网络结构简单，网络收敛速度最佳，但是要求建立足够多训练网络的样本.

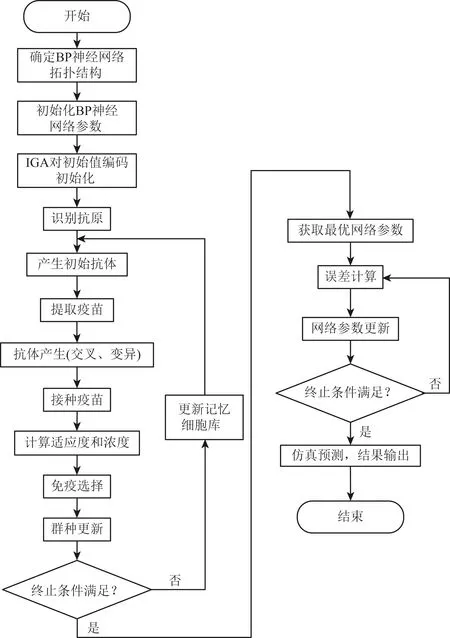
图3 免疫遗传神经网络框图Fig.3 The flowchart of Immune Genetic Algorithm

对于IGA-BP神经网络，以上四种建模方法均有不足，Singh等(2010)采用的建模方法网络结构复杂，训练样本数目过多，网络收敛速度慢；徐海浪等(2006)采用的建模方法输入输出节点过多，网络结构臃肿，参数过多，不便于IGA优化；戴前伟等(2014)采用的样本分割建模方法，虽然是输入输出节点有所减少，网络收敛速度加快，但是依然存在节点过多的问题.对于IGA优化设计来讲，参数过多容易导致优化时间较长；Ahmand等(2010a,2010b)提出了很好的建模方法，输入输出节点少，网络结构精炼，但是单个样本集数量过大.

本文充分考虑以上多种建模的优缺点，采用如下的建模方法:首先，确定模型的输入输出节点，对采集的视电阻率进行预处理，然后将预处理后的视电阻率和相应的水平、垂直位置作为网络模型输入节点，真实的电阻率作为网络模型的输出节点，这样构建的网络结构参数最小，模型结构精简，收敛速度快.其次分割训练样本集.由于单个样本集整体输入网络训练，数量过大，我们将大的样本集分隔开成多个小样本集，来训练网络，这样在保证网络收敛快的同时节约了运算时间，构建的模型反演效果更好.

为了验证不同学习算法对神经网络反演的影响，本文采用温纳-斯伦贝格装置进行测量，共使用37个测量电极，测量极距为1 m.共采集210个数据点.通过上述的讨论，本文IGA-BP神经网络模型使用三层神经网络结构.网络的样本集通过改变异常体的大小、位置、形态来获得，其中测试样本集不参与网络的训练，图4为构建的部分训练样本模型.图5为用于测试的样本模型.

其中在构建训练样本集时要尽可能考虑反演目标中异常体的形态、大小以及反演目标的周围环境测试样本集应该与反演目标较为接近.本文使用RES2DMOD软件获得的2D数据集作为训练与测试数据集.

图4 用于训练的部分样本模型Fig.4 The sample models for network training

图5 用于测试的样本模型Fig.5 The sample models for network test

在人工神经网络中，BP神经网络占据了重要的位置，许多研究对其内部的训练算法做了进一步的改进，从而提高收敛速度.其中比较有代表的是附加动量法、自适应学习速率法、弹性BP算法(简称RPROP).弹性BP算法只取偏导数符号，不考虑偏导数的幅值，偏导数的符号决定权值更新的方向.该训练算法收敛速度较前述两种方法快，因而在大量实际应用中，弹性BP算法非常有效.

Ahmand(2010a,2010b)、张凌云等(2011)均采用弹性BP算法作为网络训练算法，对于大数据来说，该算法收敛速度最快，因而在地球物理中得到广泛应用.

BP算法大多是局部优化算法，这些算法本身自然在训练过程容易陷入局部小的问题，即在训练过程中可能找不到某个具体问题的解.针对这个问题，张凌云等(2010)提出混合算法进行优化设计，并指出遗传算法优化神经网络的反演精度最高，但是基本的遗传算法优化时间过长，本文在基本遗传算法的基础上，又引进了免疫算法，通过引入免疫机制提高遗传算法的优化速度，使其在优化过程中，快速得到最佳解.

本文分别用三种算法——采用弹性BP训练算法的神经网络算法、遗传神经网络算法(简称GABP法)和免疫遗传神经网络算法(简称IGA-BP法)对所建立的训练样本集进行训练和测试.实验中算法的运行参数分别设置如下:种群规模均为100，疫苗接种概率:a=0.7，交叉概率:Pc=0.67，变异概率:Pm= 0.05，最大代数为1000，动态疫苗库的疫苗数量M=8.目标误差均设置为0.01，具体的参数设置如表1所示.

三种不同学习算法性能如表2、3所示，从中我们可以清晰地看出非线性算法混合反演的优越性，反演计算时间短、精度高.本文选取50个样本集和12个测试集进行试验验证，其中表2性能对比为50次训练的平均值，学习步数和时间均是在目标收敛的情况下.表3、4为分别使用BP法、GABP法和IGA-BP法的进行训练和测试的结果对比表，由此得到以下结论：

表1 不同算法的参数设置

(1) 针对神经网络容易陷入局部小，收敛性相对较差的问题，应用多种算法对神经网络进行权重优化，从表2中，IGA-BP神经网络算法明显优于GABP神经网络，优化时间明显少于GABP神经网络，而且迭代次数要明显少于GABP神经网络，大大节约了运算时间.

表2 反演算法权重优化过程对比

表3 三种反演算法性能对比

表4 三种反演算法试验结果对比

(2) BP神经网络法进行反演时需要用双隐含层才可以获得较好的网络进行预测，需要多次调整隐含层节点数，因此迭代次数较多、费时较长，而IGA-BP法反演和GABP反演时，由于先优化了BP神经网络初始的权阙值，所以在训练时仅单隐含层网络就可得到更优的结果，反演速度较快.

(3) 收敛比是指在50次训练的过程中收敛的次数占总数的比例，表明算法的优越性.综合对比不难发现IGA-BP反演收敛效果最好.

(4) 反演时间是指训练好神经网络的权阙值参数之后，实际反演所需的时间.IGA-BP神经网络的反演时间在相同情况之下，所需时间最短，其次为GABP神经网络，而BP神经网络的时间较长，表明神经泛化能力不及前两者.

(5) 预测误差是指参考模型输出与实际输出电阻率值的均方差值(MSE)，判断系数R2通常用于判定自变量和因变量之间的符合度，通常介于0～1之间，R2越大符合性越好(张凌云，2011；戴前伟，2014)，这两者是表明数据稳定性的参数.从三种神经网络方法的预测误差值看，IGA-BP要优于GABP和BP算法，在测试的样本模型中预测最大绝对值误差，前者仅为12.3，后两者高达32.19和82.28.因此，通过上述五点的对比，可见IGA-BP和GABP神经网络算法无论训练成功率还是数据稳定性都要明显好于BP算法.从收敛速度和运算时间上看，IGA-BP算法反演效果是最优的.

表5 反演算法试验结果对比

4 数据仿真与模型反演

为了进一步验证上述反演算法的性能，本文选择的算例模型为经典的垂直双阻模型和3个异常体的组合模型，并将其用于IGA-BP和最小二乘法RES2DINV、GABP、BP反演结果的对比.

模型1采用温纳-斯伦贝格装置，电极极距为1 m，共使用37个电极.背景场的电阻率为100 Ωm，其中的两处异常均为高阻500 Ωm，地下埋深分别为1 m和3 m，在水平16 m和19 m之间，异常体的尺寸大小均为1 m×3 m，如图6a所示.在电阻率二维神经网络反演测试中，神经网络输入节点为X、Z位置和视电阻率数据，网络输出为真实电阻率参数，网络输出的反演结果如图6所示.

从图6和表5的反演结果分析可知，从异常体形态上来看，IGA-BP神经网络反演的结果能较为准确地反应异常体的位置和电阻率，异常体形态和轮廓清晰，最小二乘法反演结果没有区分开异常体之间的间隙，IGA-BP反演效果明显优于RES2DINV软件的反演结果.从反演时间上来看，IGA-BP算法首先利用IGA法对神经网络进行初始权值、阙值的最优寻找，为神经网络算法提供较好的训练初始权值、阙值，优化好神经网络参数后，神经网络可以直接反演，而且不需要重复训练反演时间只需要1.6 s，而最小二乘法反演时间为2.7 s.仅单纯从反演时间来看，IGA-BP反演时间最短，具有较高的反演效率.

模型2为3个异常体的组合模型，主要用于检验IGA-BP和GABP、BP的反演性能的差异，模型2的基本参数设置如下：依然采用温纳-斯伦贝格装置，接收电极37个，电极极距1 m，背景场的电阻率为150 Ωm，高阻异常体1的形态大小为1 m×3 m，电阻率值为800 Ωm，在水平13 m和16 m之间，低阻异常体2的形态大小均为0.5 m×1 m，顶部埋深2 m，在水平14.75 m和15.25 m之间，电阻率值为20 Ωm，低阻异常体3的形态大小均为12 m×2 m，顶部埋深1 m，在水平25 m和37 m之间，电阻率值为20 Ωm，顶部埋深1 m，在电阻率二维神经网络反演测试中，神经网络输入节点为 X、Z位置和视电阻率数据，网络输出为真实电阻率参数，网络输出的反演结果如图7所示.

从表5和图7的反演结果分析可知，从预测误差和判断系数来看，IGA-BP算法的MSE和R2仅为3.07%和0.97，反演性能最优.从异常体形态上来看，三种神经网络反演的结果均能较为准确地反映异常体的位置和电阻率，异常体形态和轮廓都较为清晰.BP算法的反演结果在高阻异常体1、低阻异常体2处出现了较大失真，多了一些冗余构造，同时低阻异常体的电阻率值与实际差异较大.GABP反演算法较BP算法得到一些改善，但在低阻异常体2依然存在较大的失真.IGA-BP算法的反演结果与实际模型更为接近，异常体的形态结构、位置、电阻率值均得到较好的反映，证实了算法具有较好的泛化能力和稳定性.

图6 样本模型1的示意图及不同方法的反演结果(a) 模型示意图;(b) IGA-BP反演结果;(c) RES2DIV软件反演结果.Fig.6 The model 1 and inversion results of different algorithms(a) The Schematic model;(b) IGA-BP inversion results;(c) RES2DIV software inversion results.

图7 样本模型2的示意图及不同方法的反演结果(a) 模型示意图;(b) IGA-BP反演结果;(c) GABP反演结果;(d) BP反演结果.Fig.7 The model 2 and inversion results of different algorithms(a) Schematic model;(b) IGA-BP inversion results;(c) GABP inversion results;(d) BP inversion results.

图8 采空区示意图及视电阻率断面图(a) 野外示意图;(b) 视电阻率断面图.Fig.8 The schematic of Goaf and its apparent resistivity cross-sectional view(a) The Goaf schematic view;(b)The apparent resistivity cross-sectional view.

图9 不同方法的反演结果(a) IGA-BP反演结果;(b) BP反演结果;(c) 线性反演结果.Fig.9 The inversion results of different algorithms(a) IGA-BP inversion results;(b) BP inversion results;(c) RES2DIV software inversion results.

5 野外实验验证

为了进一步验证IGA-BP算法的优越性，本文进行了野外工程实验，实验区域为吉林省长春市吉林大学朝阳校区原日伪时期留下的防空洞区域，图8a为防空洞示意图.图中A处为下水管道口，下水管道口径为1 m×2 m，深度为3 m，在第12个电极和第14个电极之间.B处为防空洞区域.防空洞走向为由东向北，顶部距离地面0.5 m，深度为3 m，在第25个电极和第37个电极之间，本次探测在测区内由南向北布设1条测线，使用GenPenE60D分布式高密度电法仪器进行实地测量，采用温纳-斯伦贝格装置，电极极距为1 m，共使用37个电极，共完成测点210个.

本文用三种算法分别对采集的视电阻率进行反演成像，视电阻率断面图、反演结果分别如图8b、图9所示.由反演结果图9可知，从异常体形态上来看，IGA-BP算法和BP算法均较正确地反映了异常体的位置和电阻率值，而在异常体轮廓上IGA-BP算法反演结果更为清晰.而线性反演方法反演结果与实际结果相比失真很大，并且异常体的阻值也与实际值相差很大，无法观测数据末端的异常体.基于以上判断，不难发现IGA-BP算法的优越性，从而验证了IGA-BP算法具有较强的泛化能力和稳定性.

6 结论

本文联合多种算法实现了高密度电阻率法的非线性混合反演，克服了单独使用BP神经网络易陷入局部极小、依赖初始权阈值、反演时间长及收敛速度慢等缺点.文中提出将免疫遗传算法与神经网络混合进行反演，提出了最小精炼的反演模型结构，通过模型仿真与实验验证，并与BP等反演算法对比，该算法反演误差较小，反演时间较短，较传统的线性反演成像更加清晰准确，具有很好的应用前景.总之，IGA-BP反演方法是一种新型的直流电法非线性反演成像技术，对复杂地质构造和三维电阻率反演成像的问题，IGA-BP反演方法有待进一步进行理论研究，需在以后的工作中不断完善.

致谢 感谢吉林大学地球信息探测仪器教育部重点实验室提供了研究平台，感谢吉林大学时间域电磁组的全体成员给予的帮助和指导，感谢审稿专家对该文的审定.

References

Ahmad N，Samsudin T.2009.Using artificial neural networks to invert 2D DC resistivity imaging data for high resistivity contrast regions:A MATLAB application.Computers and Geosciences，35(11)：2268-2274.

Ahmad N，W A T.Wan.A，Samsudin T.2010a.Inversion of quasi-3D DC resistivity imaging data using artificial neural networks.Journal of Earth System Science，119(1)：27-40.

Ahmad N，W A T.Wan.A，Samsudin H.T.2010b.3D inversion of DC data using artificial neural networks.Studia Geophysica et Geodaetica，54(3)：465-485.

Calderon-Macis C，Sen I K，Stoffa P L.2000.Artificial neural networks for parameter estimation in geophysics.Geophysical Prospecting，48(1)：21-47.

Cranganu C.2007.Using artificial neural networks to predict the presence of overpressured zones in the Anadarko Basin，Oklahoma.Pure and Applied Geophysics，164(10)：2067-2081.

Dai Q W，Jiang F B，Li D.2014.Nonlinear inversion for electrical resistivity tomography based on chaotic DE-BP algorithm.Journal of Central South University.，21(5)：2018-2025.

Dai Q W，Jiang F B，Dong L．2014．RBFNN inversion for electrical resistivity tomography based on Hannan-Quinn criterion．Chinese J.Geophys.(in Chinese)，57(4)：1335-1344．

El-Qady G，Keisuke U.2001.Inversion of DC resistivity data using neural networks.Geophysical Prospecting，49(1):417-430.

Fani E A，George J T，Ioannis F G，et al.2013.Estimation of seasonal variation of ground resistance using Artificial Neural Networks.Electric Power Systems Research，94：113-121.

Jimmy Stephen，Manoj C，Singh S B.2004.A direct inversion seheme for deep resistivity Sounding data using artificial neural networks.Journal of Earth System Science，113(l):49-66.

Liu B．2010．Study on the water-bearing structure advanced detection and water inrush hazards real-time monitoring in tunnel based on the electrical resistivity method and induced polarization method [Ph．D．thesis] (in Chinese)．Shandong：Shandong University．

Luo X P．2002．The research on artificial immune genetic learning algorithm and its application in engineering [Ph．D．thesis] (in Chinese)．Hangzhou：Zhejiang University．

Poulton M，El-Fouly A.1991.Preprocessing GPR signatures for cascading neural network classification.SEG Expanded Abstracts，10(1):507-509.

Poulton M，Sternberg K，Glass C.1992.Neural network pattern recognition of subsurface EM images.Journal of Applied Geophysic，29(1):21-36.

Spichak V V，Fukuoka K，Kobayashi T.et al.2002.Artificial neural network reconstruction of geoelectrical parameters of the Minou fault zone by scalar CSAMT data.Journal of Applied Geophysics，49(1):75-90.

Singh U K，Tiwari R K，Singh S B.2005.One-dimensional inversion of geo-electrical resistivity sounding data using artificial neural networks—a case study.Computers &Geosciences，31(1):99-108.

Singh U K，Tiwari R K，Singh S B.2010.Inversion of 2-D DC resistivity data using rapid optimizationand minimal complexity neural network.Nonlinear Processes in Geophysics，17(1):65-76.

Mann C J H .2006.Geophysical Applications of Artificial Neural Networks and Fuzzy Logic.Kybernetes，35(1):3-4.

Shan W T，Chen X A，He Y，et al． 2013．Application of immune genetic algorithm based fuzzy RBF neural Network in high-speed motorized spindles．Chinese Journal of Mechanical Engineering (in Chinese)，49(23)：167-173．

Maiti S，Gupta G，Erram V C.2011.Inversion of Schlumberger resistivity sounding data from the critically dynamic Koyna region using the Hybrid Monte Carlo-based neural network Approach.Nonlinear Processes in Geophysics.，18(2):179-192.

Marina R C，NiklasL，Thomas K，Jasper A.2014.Vrugt Two-dimensional probabilistic inversion of plane-wave electromagnetic data:methodology，model constraints and joint inversion with electrical resistivity data.Geophysical Journal International，196 (3)：1508-1524.

Vladimir M，Krasnopolsky.2007.Neural network emulations for complex multidimensional geophysical mappings:Applications of neural network techniques to atmospheric and oceanic satellite retrievals and numerical modeling.Reviews of Geophysics，45(1):RG3009.

Xu H L,Wu X P．2006．Inversion of 2D resistivity neural networks．Chinese J.Geophys.(in Chinese),49(2)：584-589．

Zhang L Y,Liu H F．2011． The application of ABP method in high-density resistivity method inversion． Chinese J.Geophys.(in Chinese)，54(1)：227-233．

Zhang L Y．2011．The study of nonlinear inversion method in high-density resistivity method inversion[Ph．D．thesis] (in Chinese)．Taiyuan：Taiyuan University of Technology．

Zhou M，Sun S D．1999．Genetic Algorithm Theory and Application (in Chinese)．Bengjing：National Defense Industry Press．

附中文参考文献

戴前伟，江沸菠，董莉.2014.基于汉南-奎因信息准则的电阻率层析成像径向基神经网络反演.地球物理学报,57(4):1335-1344.

单文桃，陈小安，合烨等.2013.基于免疫遗传算法的模糊径向基函数神经网络在高速电主轴中的应用.机械工程学报，49(23):167-173.

刘斌.2010.基于电阻率法与激电法的隧道含水地质构造超前探测与突水灾害实时监测研究[博士论文]．山东：山东大学.

罗小平.2002.人工免疫遗传学习算法及其工程应用研究[博士论文].杭州:浙江大学.

徐海浪，吴小平.2006.电阻率二维神经网络反演.地球物理学报，49(2):584-589.

张凌云，刘鸿福.2011.ABP法在高密度电阻率法反演中的应用．地球物理学报，54(1)：227-233.

张凌云.2011.高密度电阻率勘探反演的非线性方法研究[博士论文].太原:太原理工大学.

周明，孙树栋.1999.遗传算法原理与应用.北京:国防工业出版社.

(本文编辑 汪海英)

Evaluation of reservoir permeability using array induction logging

ZHOU Feng1,2,MENG Qing-Xin3,HU Xiang-Yun2*,SLOB Evert4,PAN He-Ping2,MA Huo-Lin2

1 School of Mechanics and Electronic Information,China University of Geosciences,Wuhan 430074,China2 Hubei Subsurface Multi-scale Imaging Key Laboratory,Institute of Geophysics and Geomatics, China University of Geosciences (Wuhan),Wuhan 430074,China3 Exploration Technology and Engineering College,Hebei GEO University,Shijiazhuang 050031,China 4 Faculty of Civil Engineering and Geosciences,Delft University of Technology,Delft 2628 CN,the Netherlands

During drilling,the mud column sustains a slightly higher pressure than the formation to maintain the stability of the well wall,which causes the mud filtrate to penetrate into formation pores and displace in-situ fluids.The invasion depth is affected by reservoir properties,especially the reservoir permeability.Therefore,it is possible to estimate the reservoir permeability if the invasion depth can be measured.

Array induction logging;Permeability evaluation;Mud invasion

基于IGA算法的电阻率神经网络反演成像研究

Research of resistivity imaging using neural network based on immune genetic algorithm

GAO Ming-Liang，YU Sheng-Bao，ZHENG Jian-Bo，XU Chang，LIU Wei-Yu，LUAN Hui*

College of Instrumentation and Electrical Engineering，Jilin University，Changchun 130026，China

周峰，孟庆鑫，胡祥云等.2016.利用阵列感应测井进行储层渗透率评价.地球物理学报，59(11):4360-4371,

10.6038/cjg20161135.

Zhou F,Meng Q X,Hu X Y,et al.2016.Evaluation of reservoir permeability using array induction logging.Chinese J.Geophys.(in Chinese),59(11):4360-4371,doi:10.6038/cjg20161135.

国家自然科学基金(41674138，41304082，41304078)，中国石油科技创新基金(2015D-5006-0304)，油气资源与探测国家重点实验室开放基金(PRP/open-1302)资助.

周峰，男，1979年生，副教授，博士，研究方向为井中电磁法.E-mail：zhoufeng617@163.com

*通信作者 胡祥云，男，1966年生，教授，博士生导师，研究方向为电磁勘探方法.E-mail：xyhu@163.com

10.6038/cjg20161135

P631 收稿日期2015-05-26，2016-09-20收修定稿

�� 中图分类号 P631

2015-09-02，2016-09-27收修定稿

A numerical study was conducted to investigate the feasibility of evaluating reservoir permeability with array induction logging.A mud invasion model was built up by coupling mud cake growth with multiple-phase fluid flow,and an array induction logging model was established based on the Born geometric factor theory.Joint forward simulations of mud invasion and array induction logging indicated that the responses of array induction logging can reflect the effect of mud invasion on the formation resistivity.Inversion based on the damped least square method revealed that the invasion depth can be acquired from array induction logging data.

We investigated the association between reservoir permeability and invasion depth,and found that in a reservoir with a permeability of 1 to 100 mD (1 mD= 0.987×10-3μm2),the reservoir permeability governs the invasion depth,and thus the permeability can be evaluated according to invasion depth.A two-dimensional numerical simulation showed that the inversed invasion depth curve had a similar fluctuation to the permeability variation.For a layered formation,a series of interpretation charts can be produced to evaluate the permeability of every layer with tolerable errors.The numerical investigation proves the feasibility of estimating reservoir permeability with array induction logging.