煤与瓦斯突出数学模型及三维数值模拟
刘雪琴,李会谦,冯 哲
(1.北京达飞安评管理顾问有限公司,北京 100101;2.北京矿冶研究总院,北京 100160;3.北京燃气昌平有限公司,北京 102200)
煤与瓦斯突出数学模型及三维数值模拟
刘雪琴1,李会谦2,冯 哲3
(1.北京达飞安评管理顾问有限公司,北京 100101;2.北京矿冶研究总院,北京 100160;3.北京燃气昌平有限公司,北京 102200)
为研究掘进过程中瓦斯压力变化规律,从孔隙率定义出发推导出孔隙率与渗透率的动态模型方程,并通过建立含瓦斯煤压力场控制方程得到含煤与瓦斯突出数学模型。以阳煤五矿赵家分区煤矿为例,通过FLUENT对建立煤与瓦斯突出数学模型进行了对应的三维数值模拟研究。结果表明,随着掘进工作的进行,瓦斯卸压区域渐渐扩大,渗透率随之改变,最后瓦斯流动速率慢慢加快,离掘进面愈近的地点瓦斯压力降低速率愈高。在具备了瓦斯异常涌出的物质、动力和构造条件后,深部含瓦斯煤层在很大程度上会伴有瓦斯异常涌出和瓦斯浓度超标的现象,对现场瓦斯防治工作提供相应理论指导。
煤;瓦斯;突出数学模型;三维数值;模拟;参透率
我国95%的煤炭属于地下开采,赋存条件差,在煤矿深部巷道掘进的过程中,由于地应力及地质条件的影响,会引起围岩变形破坏,导致煤与瓦斯突出事故,严重威胁着煤矿安全高效生产和矿山工作人员的生命安全。因此对于煤与瓦斯突出的研究工作拥有特别重要的理论和实际意义[1-2]。文章通过对煤与瓦斯运移规律进行研究来预测、控制及防止煤和瓦斯突出这一灾害,结合理论方程,针对阳煤五矿赵家分区的地质情况和开采技术条件构建煤与瓦斯突出数学模型,运用FLUENT对建立的数学模型进行了对应的三维数值模拟研究,对深入认识煤与瓦斯突出机理、指导预防措施等具有理论意义和实用价值。
1 瓦斯流动数学模型
1.1 模型构建的基本假设
深层煤岩体施工过程复杂,所有的因素不能一一考虑,为更精确地描述受扰动影响的含瓦斯煤体的气固相互影响作用,引入如下几个基本假设[3-5]:①含瓦斯煤体为各向同性弹塑介质;②在瓦斯运移和煤体变形过程中温度保持不变;③含瓦斯煤体的变形为小变形;④瓦斯在煤岩中的渗流服从Darcy定律;⑤瓦斯的吸附解服从Langmuir平衡方程,并且假设煤体只吸附瓦斯。
1.2孔隙率和渗透率动态模型方程
含瓦斯煤岩在加载过程中,随着变形的增加,等效孔隙度(φ)和渗透率(k)是动态变化的。在建立含瓦斯煤岩本构模型时,应考虑这些因素的变化和影响。
(1)孔隙率动态模型。①当含瓦斯煤岩处于弹性变形阶段时。孔隙率是孔隙裂隙介质体积与多孔介质总体积之比。含瓦斯煤体的孔隙率是动态变化的,设煤固体骨架体积用表示,表示其变化;煤外观总体积用表示,表示其变化,煤的孔隙体积用表示,表示其变化。由孔隙率的定义可知[6]:
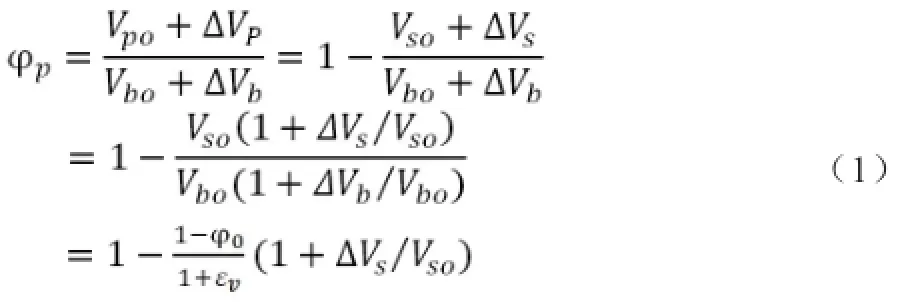

岩石试件在受压情况下,当达到峰值强度时,开始出现宏观裂纹。因此,可假设当载荷达到峰值应力时的,可由实验得到;而当载荷达到屈服应力时,有。根据这两种情况,不难推导出,,并将之回代入式(2),得到:
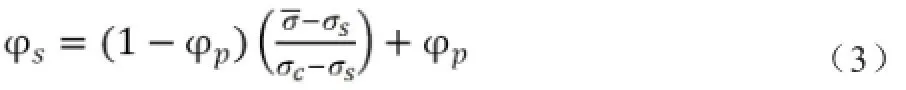
(2)渗透率动态模型。当煤体的孔隙率发生动态变化时,渗透率随之而变,从而影响煤体内瓦斯流动[7]。
根据Carman-Kozeny经验公式:

假设初始状态煤体渗透率为:


孔隙体积的变化为:

改变后的孔隙率为:
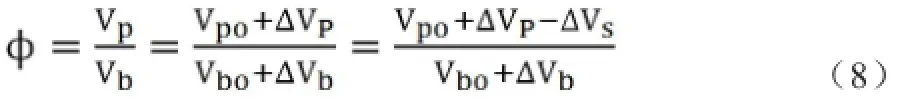

1.3含瓦斯煤压力场控制方程
(1)渗流运动方程。研究表明瓦斯在低渗透率多孔介质中运移时,在固体壁面存在滑脱效应[8]。阳煤五矿赵家分区15#煤层多为高瓦斯及低渗透煤层,因此,考虑滑脱效应时,煤层中瓦斯的运动方程可表示为:


(3)煤体瓦斯含量方程。瓦斯气体的解吸和吸附随瓦斯压力变化的关系满足朗格缪尔方程,所以有煤层吸附瓦斯含量计算公式[9]为例:

式中,a为吸附常数,m3/kg,b为吸附常数,MPa-1,c为煤质校正参数,kg/m3,,为煤的密度,kg/m3;M为煤的水分,%;A为煤的灰分,%。煤层中游离瓦斯气体含量为:

(4)渗流连续方程。根据质量守恒定律,煤层瓦斯流动的方程为:

式中:M为煤体瓦斯瓦斯含量;V为瓦斯渗流速度,m/s。联合式(1),(10) ~ (13),可得渗流方程为:
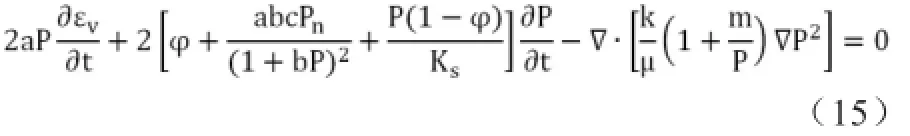
2 数值模拟及结果分析
2.1几何模型的建立
根据假设条件,以阳煤五矿赵家分区内15号煤层赋存为依据,对依据模型的几何尺寸构建三维计算进行网格划分,细化煤层以及周围的岩网格适当粗划剩下网格部分,最后总共划了207 200个单元,218 766个节点。煤层原始瓦斯压力为1.0MPa,在模型顶部施加20.17MPa的均布载荷用来模拟上覆岩层自重作用,底部为固定边界,前后左右设定为法向约束边界。
利用煤岩体变形与瓦斯渗流相互作用下的弹性损伤程序进行数值计算,表1为瓦斯流动计算的相关参数。

表1 煤层主要相关物性参数
2.2三维数值模拟结果分析
根据以上条件,对该模型进行数值模拟,以8134工作面上顺槽独巷掘进为对象进行模拟计算。当地应力达到真实情况之后,对巷道内单元设置为空单元。煤体掘进后造成应力场的重新分布,对开挖过程后的渗流场数值模拟结果进行分析。
在独巷掘进过程中,处于掘进工作面前方煤体中的裂隙持续变化,煤体中的瓦斯在这些孔隙中流动,由于扩散效应,瓦斯从高浓度流向低浓度空间,到达巷道中。独巷掘进开采时,破坏了巷道周围的煤岩,巷道围岩应力重新分布,损伤逐渐加剧,裂隙重组,煤层的孔隙率和渗透率随之改变。对孔隙率和渗透率进行归一化处理,图1、图2 分别表示掘进开采时前方煤体孔隙率比率和渗透率比率的规律分布。
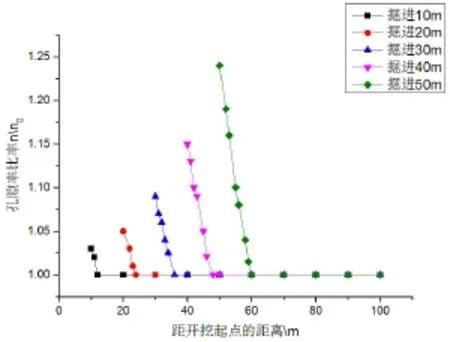
图1 掘进面前方煤体孔隙率比率分布规律

图2 掘进面前方煤体渗透率比率分布规律
通过FLUENT软件根据得到的孔隙率和渗透率的变化分布规律,对五矿赵家分区独巷掘进过程中的瓦斯压力变化规律模拟分析。渗流场初始化为均匀分布的瓦斯压力,并固定模型边界位置的瓦斯压力值,在巷道开挖后,对挖空单元赋予固定的大气压力值。同时为了简化模型,提高计算速度,假设整个模型中煤层厚度很大,忽略了支护结构和岩层的影响。
图3至6分别给出了煤岩巷道横切面(x=0)和纵切面(z=12)上,在掘进过程中煤岩体中瓦斯压力的变化规律。开挖深度分别为10m、20m、30m、50m。
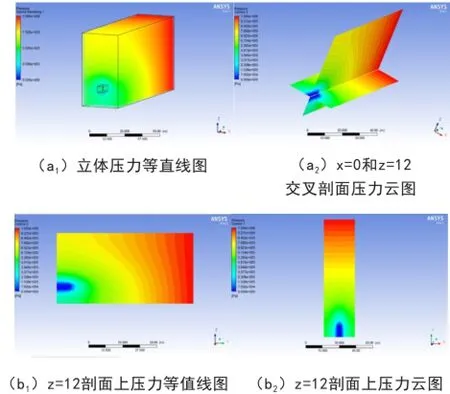
图3 开挖10m 时瓦斯压力变化分布规律
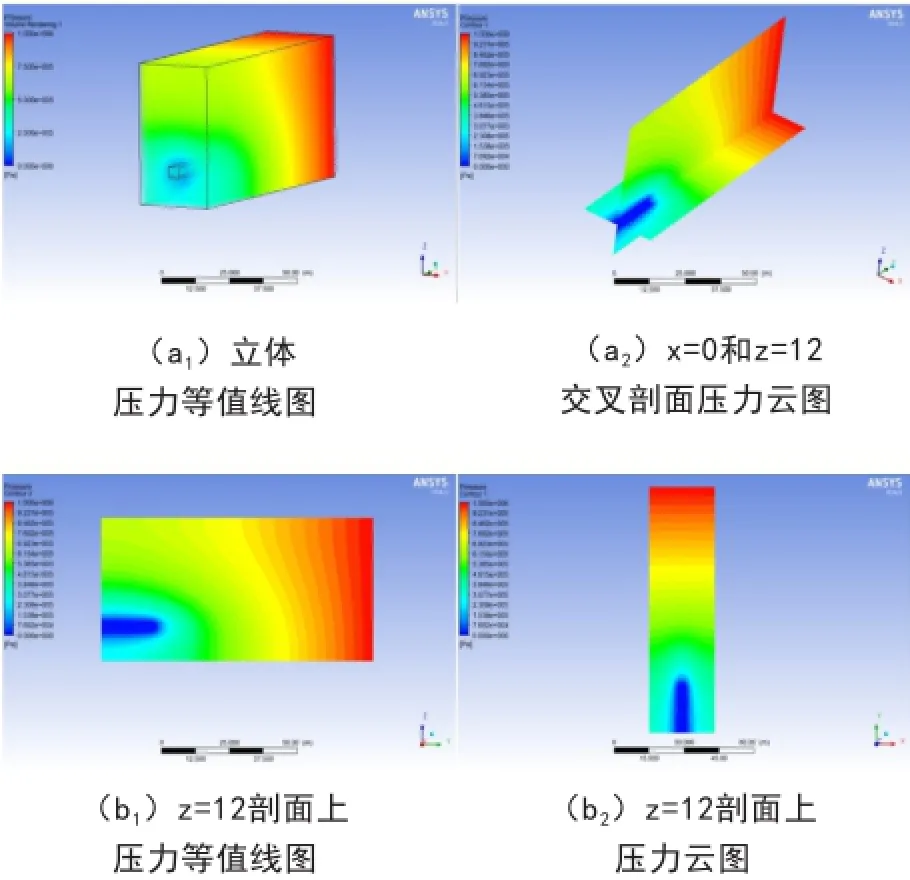
图4 开挖20m 时瓦斯压力变化分布规律
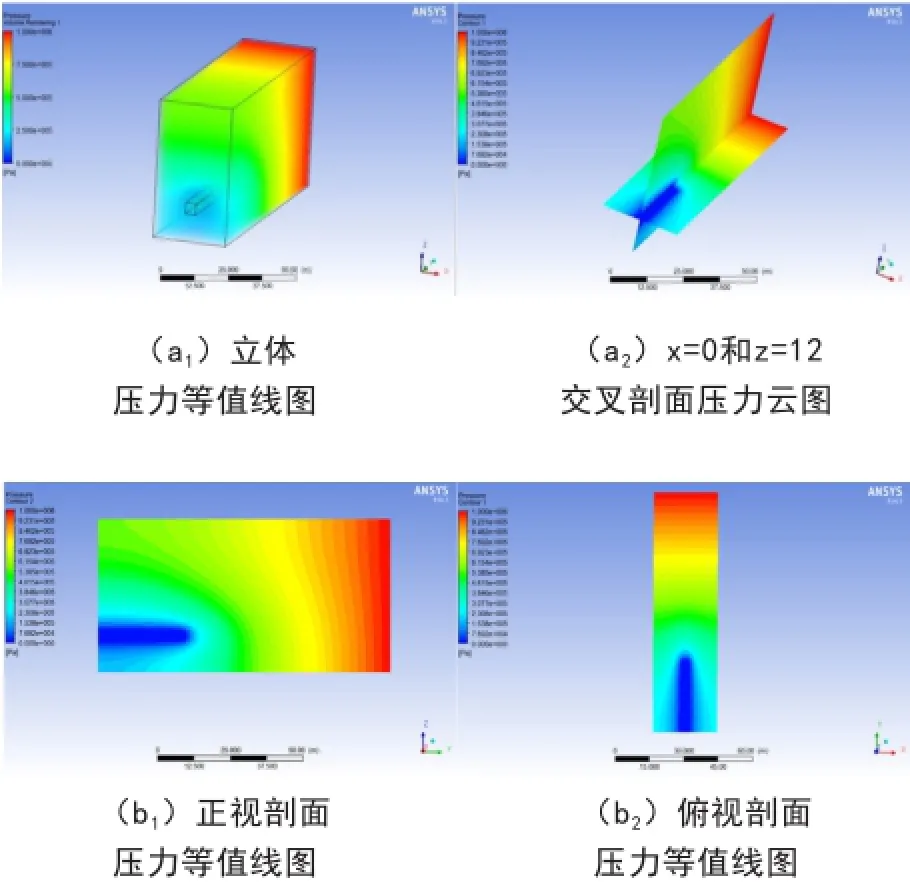
图5 开挖30m 时瓦斯压力变化分布规律
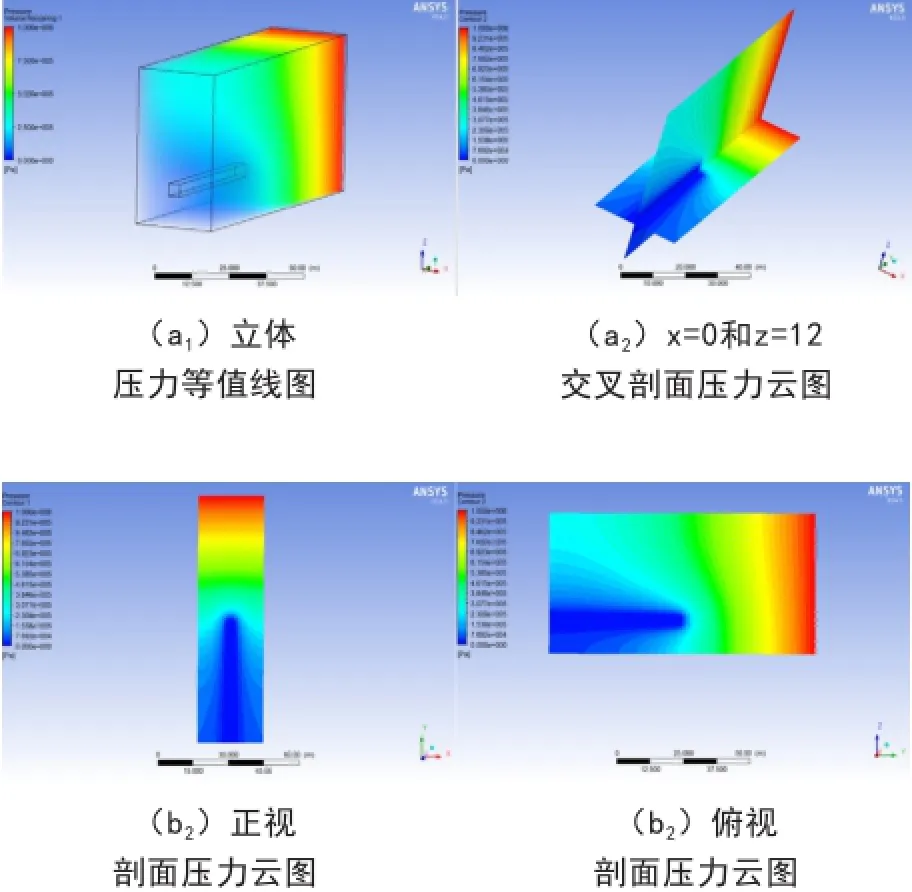
图6 开挖50m 时瓦斯压力变化分布规律
由图3至6可以看出,当开挖到10m时,开始阶段,围岩破坏较轻,煤体渗透率较低,导致瓦斯涌入巷道内的流动速度较慢,同时围岩内瓦斯由于压力降低而不断解吸,所以在当开挖10m时,瓦斯压力降低较小,在距离巷道0.7m以内的围岩卸压明显。随着继续向前掘进,当开挖到20m时,由于围岩破损提高了煤体的透气性,瓦斯流动速度增加,瓦斯压力降低范围增大,距离巷道1m以内的围岩卸压明显。当开挖到30m时,瓦斯压力降低范围逐渐增大,距离巷道1.5m以内的围岩卸压明显。当开挖到50m时,距离巷道3m以内的围岩卸压明显,最小瓦斯压力约为0.231MPa。在靠近煤巷壁面的位置,煤体破损严重,造成瓦斯释放完全,瓦斯压力值较低。
2.3工作面掘进过程中煤体瓦斯压力变化规律
为更加具体地研究工作面掘进过程中煤体瓦斯压力变化规律,在煤层中沿工作面掘进方向巷道中心线上瓦斯压力变化曲线如图7所示。
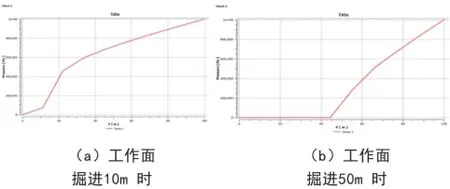
图7 工作面掘进方向煤层瓦斯压力变化分布曲线
从图7可知,在巷道持续掘进过程中,当开始掘进10m时,掘进面前方的瓦斯压力缓慢降低,影响范围较小。在继续开挖的过程中,随着时间的延长,掘进面前方煤层损伤程度及范围继续扩展,同时,卸压影响范围明显扩大,压力值显著降低。当掘进到50m位置时,瓦斯压力降低梯度也明显增大,渗透率显著提高。这都是因为掘进对于煤层的影响,致使掘进面前方的煤体产生了很多裂隙,渗透率渐渐升高,未开挖处煤层中的高浓度瓦斯经此通道流向巷道中,引起瓦斯压力在掘进面前方重新分布。
3 结论
(1)随着掘进工作的进行,由于掘进对于煤层的影响,致使掘进面前方的煤体产生了很多裂隙,掘进面前方高浓度瓦斯经裂隙流向巷道,引起瓦斯压力在掘进面前方重新分布。瓦斯卸压区域渐渐扩大,渗透率随之改变,最后瓦斯流动速率慢慢加快,离掘进面愈近的地点瓦斯压力降低速率愈高。
(2)深部开采的煤层中,在开采震动和扰动下,煤层裂隙中瓦斯解吸膨胀的能量和动力很高。开挖加、卸载下的层裂、离层与瓦斯解吸膨胀相互作用模式,和地下开挖导致应力重新分布,导致煤岩体产生微破裂,产生贯通裂带。瓦斯通过裂隙大量涌出,造成围岩瓦斯压力下降,致使煤体有效应力增高,煤体进一步损伤破裂。因此,在具备了瓦斯异常涌出的物质、动力和构造条件后,深部含瓦斯煤层在很大程度上会伴有瓦斯异常涌出和瓦斯浓度超标的现象。
[1] 李晓泉.含瓦斯煤力学特性及煤与瓦斯延期突出机理研究[D].重庆大学,2010.
[2] HiIdenbrand A,Krooss B M,Busch A.EvoIution of methane sorption capacity of coaI seams as a function of buriaI history:A case study from the Campine Basin [J]. Int.J.CoaI GeoI,2006,(66).179-203.
[3] 汪有刚,刘建军,杨景贺,等.煤层瓦斯流固耦合渗流的数值模拟[J].煤炭学报,001,26(3):286-289.
[4] 梁冰,刘建军,范厚彬,等.非等温条件下煤层中瓦斯流动的数学模型及数值解法[J].岩石力学与工程学报,2000,19(1):1-5.
[5] 薛东杰,周宏伟,唐咸力,等.采动煤岩体瓦斯渗透率分布规律与演化过程[J].煤炭学报,2013,38(6):32-37.
[6] 李培超,孔祥言,卢德唐.饱和多孔介质流固耦合渗流的数学模型[J].水动力学研究与进展(A辑),2003,18(4):419-426.
[7] 陈育民. FLAC/FIAC3D基础与工程实例(第二版)[M].北京:中国水利水电出版社,2013.
[8] 肖远见.沿层钻孔周围瓦斯(真实气体)渗流压力方程及三维数值分析[J].矿业安全与环保,2004,31(3):41-43.
[9] 郭平,曹树刚,张遵国,等.含瓦斯煤体固气祸合数学模型及数值模拟[J].煤炭学报,2012,37(增2):330-335.
Mathematical Model and Three-dimensional Numerical Simulation of Coal and Gas Outburst
Liu Xueqin1,Li Huiqian2,Feng Zhe3
(1.Beijing Dafei Risk Assessment and Management Adviser Co.Ltd. Beijing, 100101; 2.Beijing General
Research Institute of Mining and Metallurgy, Beijing,100160; 3.Beijing Gas Changping Co.Ltd. Beijing,102200)
To obtain gas pressure variation in the process of coal mine roadway drivage, the dynamic model equation of porosity and permeability were derived in terms of the basic definition of porosity, and building coal-bearing and gas outburst mathematical model by coal containing gas pressure control field equation. According to the coalmine of Yangmei Minmetals, FLUENT was used to three-dimensional numerical simulation of mathematical model of coal and gas outburst. The result shows that gas pressure relief area gradually expanded, and permeability changed, finally gas flow rate accelerated slowly. The closer the driving surface is, the higher gas pressure reduction rate is. So it has significant means for guiding the gas drainage design.
Coal ;gas;outburst mathematical model;three-dimensional numerical;simulation;Permeability
TQ018
A
1671-3818(2016)09-0022-04

