考虑扇出重汇聚效应的组合电路软错误率评估

闫爱斌,梁华国,许晓琳,袁德冉

(1.合肥工业大学 计算机与信息学院,安徽 合肥 230009; 2.合肥工业大学 电子科学与应用物理学院,安徽 合肥 230009)



考虑扇出重汇聚效应的组合电路软错误率评估

闫爱斌1,梁华国2,许晓琳2,袁德冉2

(1.合肥工业大学 计算机与信息学院,安徽 合肥 230009; 2.合肥工业大学 电子科学与应用物理学院,安徽 合肥 230009)

为了准确评估集成电路的软错误率(soft error rate,SER),文章提出一种新颖的电路SER评估方法。通过门级仿真获得逻辑门输出信号,将产生瞬态故障的逻辑门进行故障注入,然后使用考虑扇出重汇聚的敏化路径逼近搜索算法查找不同输入向量下的敏化路径;通过单指数电流源模拟瞬态故障脉冲的产生,并将脉冲在敏化路径上传播,使用脉冲屏蔽模型评估电气屏蔽和时窗屏蔽效应;最后采用该方法计算可得电路总体SER。实验结果表明,由于考虑扇出重汇聚的影响,该方法平均提高8.2%的SER评估准确度。

单粒子瞬态;逻辑屏蔽;扇出重汇聚;软错误率;失效概率

0 引 言

纳米工艺下,由α粒子、质子或中子撞击电路产生的瞬态故障依然是导致电路发生软错误的重要原因[1]。随着工艺尺寸的不断缩减,组合逻辑节点电容与工作电压呈现减少趋势,致使电路对软错误的敏感性越发突出,引起电路设计者的广泛关注[1-3]。因此,在设计阶段进行软错误率(soft error rate,SER)的准确评估并进行选择性加固[4],能够为高可靠的集成电路设计提供参考,具有重要研究意义。

近年来国内外出现了较多基于软件仿真的组合电路SER评估方法。目前国际上较为典型的方法有美国加州大学的BFIT[5]、伊利诺伊大学的SERA[6]、德克萨斯大学的FASER[7]以及卡内基梅隆大学的MARS-S[8]等。BFIT方法计算速度较快,但由于未考虑扇出重汇聚效应,计算结果存在偏差。SERA方法计算精度较高,但在分析较大规模的电路SER时速度较慢。FASER、MARS-S方法采用符号化的决策图来计算组合电路SER,由于分析较大规模的电路SER时可能会发生潜在的“内存爆炸”问题,因而适用性较差。

国内众多学者也对组合电路的SER评估方法进行了深入研究。文献[9]提出一种基于混合模拟的计算组合电路SER的方法与工具,该方法综合单脉冲传播模拟算法并使用HSPICE对多脉冲传播进行仿真,计算精度高,但计算速度较慢;文献[10]提出基于频域的组合逻辑电路SER分析方法,取得了较高的计算准确度;文献[11]提出组合电路的SER自动分析平台,取得了与同类文献相似的结果;文献[12]提出一种快速而准确的SER启发式评估方法,由于未考虑扇出重汇聚的影响,计算结果存在偏差。

综合以上文献,本文提出一种考虑扇出重汇聚效应的组合电路SER评估方法。在门级仿真后通过翻转逻辑门输出信号进行故障模拟,使用考虑扇出重汇聚的敏化路径逼近搜索算法查找敏化路径;通过单指数电流源模拟粒子撞击电路敏感节点产生的单粒子瞬态故障脉冲,并将脉冲在敏化路径上传播,使用电气屏蔽和时窗屏蔽模型评估电气屏蔽和时窗屏蔽效应;进而通过提出的SER评估方法计算可得电路总体SER。由于本文方法考虑了扇出重汇聚的影响,因此提高了SER评估的准确度。

1 单粒子瞬态脉冲屏蔽效应评估

粒子撞击组合逻辑门的晶体管敏感区将会导致半导体材料发生电离,并在其轨迹上产生淀积电荷。当存在电场时,粒子轨迹上的电子空穴对将会被电极收集,形成瞬时电流。该情况若发生在组合电路中,较大的瞬时电流将会使得逻辑门的输出电压发生瞬态的变化,从而发生单粒子瞬态(single event transient,SET),表现为SET脉冲。SET瞬态故障若沿数据通路向下游传播,可能引发软错误并导致电路失效。

SET脉冲沿数据通路向下游传播会受到3种屏蔽效应的影响[5-6]:① 逻辑屏蔽,即当产生SET脉冲的门节点存在扇出门,由于受到扇出门控制值的影响,不存在到达锁存器或主输出的数据通路,脉冲被屏蔽;② 电气屏蔽,即在数据通路上传播的SET脉冲由于受到若干逻辑门的削弱作用,其宽度/幅值变小,脉冲被削弱;③ 时窗屏蔽,即到达锁存器的脉冲由于未落在有效的锁存窗口之内,或其有效宽度/幅值较小,不满足锁存器的采样时间,脉冲被屏蔽。

组合逻辑门对SET脉冲屏蔽效应示意图如图1所示。粒子撞击逻辑门G1,并在其输出端y1产生SET脉冲,当扇出门G3的输入引脚y2为0信号,由于受到该控制值的影响,不存在到达锁存器LA1的数据通路,脉冲被逻辑屏蔽。当y2为1信号,SET脉冲穿过G3从而到达输出端y3,脉冲宽度/幅值被削弱,即电气屏蔽。到达LA1的SET脉冲,未能落在有效的锁存窗口内,具体如图1下半部分的时序图所示,脉冲被时窗屏蔽。

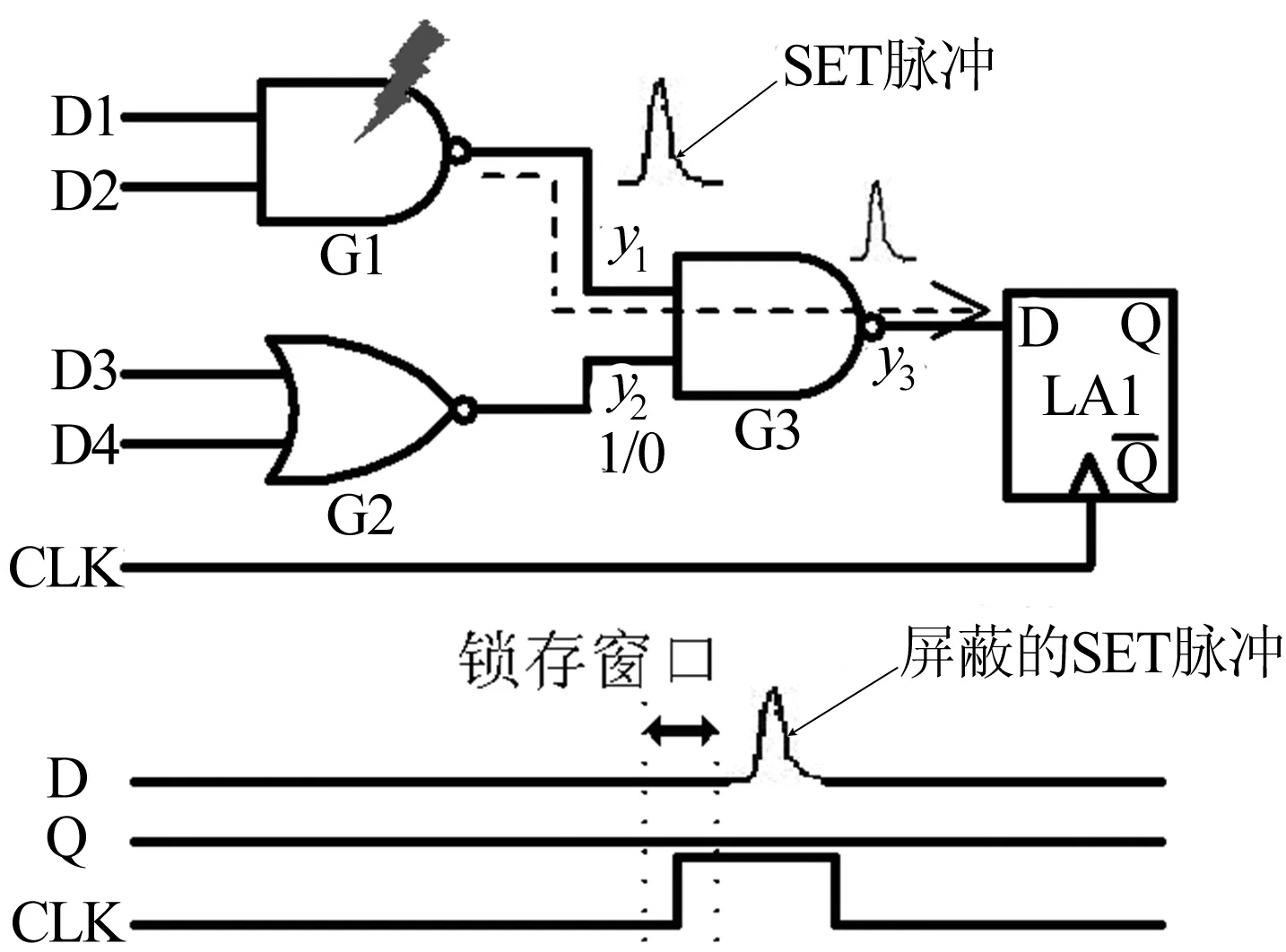
图1 组合逻辑门对SET脉冲的屏蔽效应

1.1 逻辑屏蔽效应评估

由图1可知,产生的SET脉冲若存在到达LA1的数据通路,则可能被LA1捕获,从而发生软错误,该数据通路被称作敏化路径。显然,处在敏化路径上的门节点产生的SET脉冲不会被逻辑屏蔽,本文以此评估组合逻辑对SET脉冲的逻辑屏蔽效应。敏化路径的准确搜索是本文的重要工作之一。由于忽略扇出重汇聚会引入很大偏差[13],本文提出考虑扇出重汇聚的敏化路径逼近搜索算法1。

算法1 FindSensPathsByInjFaults

∥输入:初始敏化路径与延迟链表lstSensPathAndDelayInitial,故障门gFtSrc,目标锁存器gFtDst。

∥输出:整体敏化路径与延迟链表lstSensPathAndDelayTotally。

对故障门的扇出进行广度优先搜索(breadth first search,BFS)并记录故障敏化扇出门;

∥故障敏化扇出门数据结构为list〈gate*〉 lstFoSensGates

for lstFoSensGate ← lstFoSensGates.begin() to lstFoSensGates.end() do

建立当前敏化路径与延迟链表lstSensPathAndDelayCurrent;

将lstSensPathAndDelayInitial数据记入lstSensPathAndDelayCurrent;

查找敏化引脚对应延迟并将lstFoSensGate与延迟记入lstSensPathAndDelayCurrent;

if (lstFoSensGate逼近到达gFtDst)

将链表lstSensPathAndDelayCurrent记入链表lstSensPathAndDelayTotally;

else

gFtSrc=lstFoSensGate;

FindSensPathsByInjFaults(lstSensPathAndDelayCurrent,gFtSrc,gFtDst);

end if

end

在算法准备阶段,在门级仿真后,对受到粒子撞击的逻辑门输出信号进行翻转以模拟故障注入,通过二次门级仿真将故障向下游传播,由此确认待存储逻辑值可能会发生翻转的锁存器集合。算法将该集合的元素分别作为目标锁存器gFtDst,将模拟故障注入的逻辑门作为故障门gFtSr,将故障门与零延迟数据对作为初始敏化路径与延迟链表的元素。

在算法执行阶段,首先对故障门的扇出进行广度优先搜索并记录故障敏化扇出门,然后分别将故障敏化门及其敏化引脚延迟记录到当前敏化路径与延迟链表中;若故障敏化门已逼近到达目标锁存器,则将当前敏化路径与延迟链表记录到整体敏化路径与延迟链表中;否则便将故障门设定为当前故障敏化门并递归调用该算法。

在算法收尾阶段,对故障门输出信号和扇出锥的逻辑门信号进行恢复,从而达到清除故障的目的。对所有内部节点重复如上操作,由此可得考虑扇出重汇聚的全部敏化路径。

在如上包含深度优先搜索及广度优先搜索的混合搜索过程中,利用类似动态规划的敏化路径搜索方法进行敏化路径与延迟链表的建立、查询与更新,最终只将能够到达目标锁存器的链表记录到整体敏化路径与延迟链表中而得解。

s27电路网表如图2所示。简单起见,向其输入端〈G0,G1,G2,G3,G5,G6,G7〉施加输入向量V=〈0,1,0,0,0,1,0〉,通过门级仿真得到每个逻辑门的输入输出信号。其中,器件内部标识的数字为V下的逻辑门输入引脚信号。此时,以目标锁存器LA3为例,基于该算法,可以找到如下4条敏化路径:

π1=〈G10,LA3〉,

π2=〈G14,G10,LA3〉,

π3=〈G14,G8a,G8b,G15a,G15b,G9,G11,G10,LA3〉,

π4=〈G14,G8a,G8b,G15a,G15b,G9,G11,G10,LA3〉。

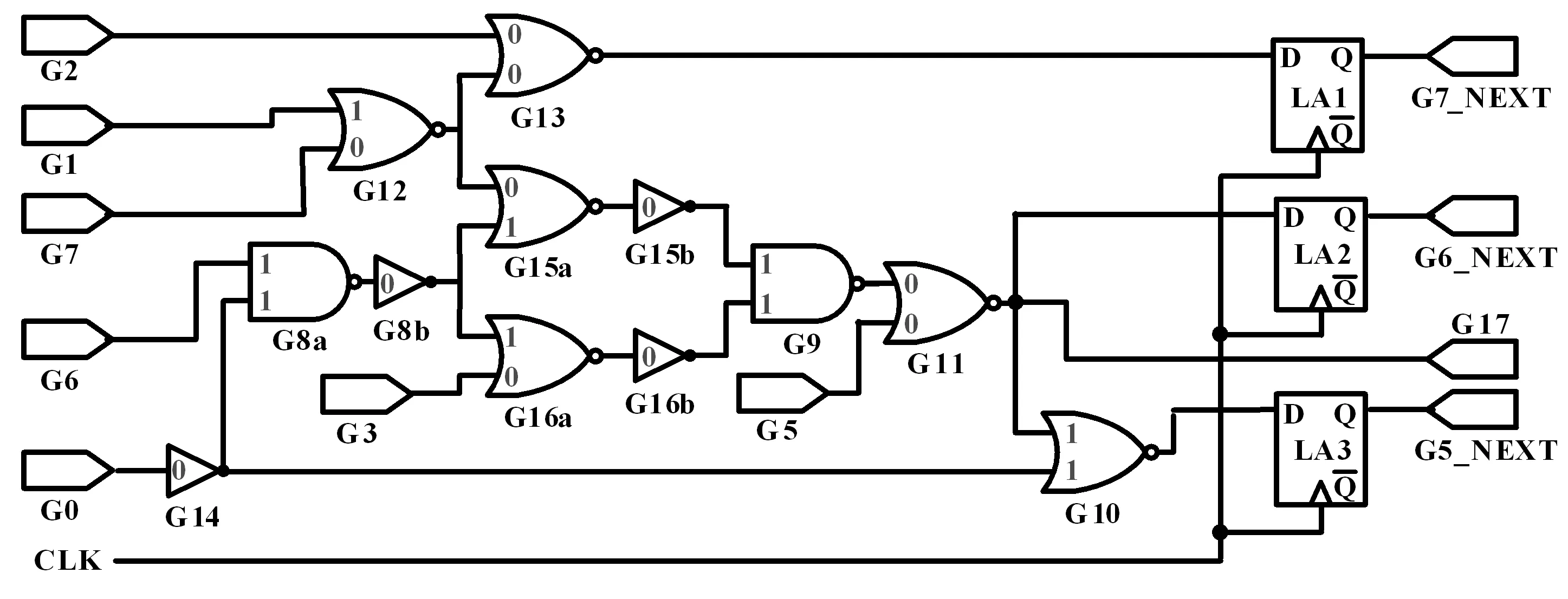
图2 s27电路网表

由于G10紧邻LA3,显然,π1为一条敏化路径。由于扇出重汇聚效应,扇出点G14输出端翻转必然导致汇聚点G9和G10的2个输入信号发生翻转,并且由于G14输出端翻转导致π3和π4中其他逻辑门也发生翻转,因此有π2、π3、π4。分析不存在其他敏化路径的原因,以G8b为例,由于G8b输出端翻转将导致G9的2个非控制值引脚发生翻转,但最终被G10的控制信号1(G14的输出信号)所屏蔽,因此不存在其他敏化路径。

与此同时,仍然以目标锁存器LA3为例,使用不考虑扇出重汇聚的搜索算法,仅可找到1条敏化路径π1,不存在π2、π3和π4。这是因为,π2被G11输出端控制信号所截断,π3和π4被G14输出端控制信号所截断,认为到达G10的2个输入引脚的信号是独立的。上述示例表明,忽略扇出重汇聚会导致搜索到的敏化路径条数减少。

另一方面,同样以汇聚点为NOR2的情形为例,使用回溯法可以找到这样一组输入向量使得汇聚点的2个输入引脚信号相异,那么可能存在这样一种情形使得扇出点输出端的翻转仍然保持汇聚点的2个输入引脚信号相异,此时扇出点到汇聚点的后继并不存在敏化路径。但是扇出点输出端的翻转可能将汇聚点唯一的控制信号变为非控制信号,此时若忽略扇出重汇聚效应,将导致汇聚点的输出端发生翻转,增加了敏化路径条数。即此时忽略扇出重汇聚将导致敏化路径条数增加。由此可见,不考虑扇出重汇聚的影响,可能导致敏化路径条数增加,也可能导致其减少,从而影响敏化路径的准确查找,以及对SET脉冲电气屏蔽和时窗屏蔽效应的评估。

1.2 电气屏蔽与时窗屏蔽效应评估

处于敏化路径上的门节点产生的SET脉冲若传播到锁存器,可能发生软错误并导致电路失效。因此需要在敏化路径上进一步分析SET脉冲的电气屏蔽与时窗屏蔽效应。

本文使用的电气屏蔽模型[14]如下:

(1)

其中,Tpwi为到达逻辑门G的SET脉冲初始宽度;Tpwo为脉冲被G削弱后的脉冲宽度余量;DG为G的敏化引脚到达输出端的平均延迟。由(1)式可知,当Tpwi过小,发生全屏蔽;当Tpwi过大,不会发生电气屏蔽;当Tpwi与DG相当,发生一定程度的电气屏蔽。

本文使用的时窗屏蔽模型[14]如下:

(2)

其中,Tpw为传播到锁存器的SET脉冲宽度,即传播到锁存器的脉冲宽度余量;Tsh为锁存元件建立与保持时间之和;Tc为电路工作时钟周期。(2)式左边为某组输入向量V下,逻辑门g产生的SET脉冲沿敏化路径传播并被锁存器l锁存的概率。由(2)式可知,当Tpw

2 组合电路SER评估

针对产生瞬态故障的各个逻辑门,将不同初始宽度的SET脉冲在敏化路径中传播,使用(1)式评估电气屏蔽效应。对于到达锁存器的脉冲,使用(2)式评估时窗屏蔽效应,由此计算不同的SET脉冲对电路造成的失效概率(failure probability,FP),从而可得该输入向量下的失效概率。从统计学角度,针对每一组输入向量重复以上操作,计算可得平均每一组输入向量下(即单个时钟周期内)的电路总体失效概率FPcomb为:

(3)

其中,N为输入向量个数;F为故障门个数;S为某组输入向量下的敏化路径条数;M为某条敏化路径上的逻辑门个数;Pi,j,k(g)为每一组输入向量下,在故障门输出端产生的SET脉冲在敏化路径上传播,经电气屏蔽后,由时窗屏蔽模型计算得到的失效概率之和,即

(4)

其中,积分项的上限与下限分别为在故障门输出端产生的SET脉冲的初始宽度上下限,(4)式中积分项为不同输入向量下,在故障门输出端产生的SET脉冲沿敏化路径传播,并被锁存器锁存的概率,通过(2)式进行评估。Gflt为敏化路径上的第1个逻辑门,当使用算法1搜索敏化路径时,Gflt为故障门。g为敏化路径上的任意逻辑门,它包含Gflt。由(4)式可知,非故障门不会发生故障,并且可对SET脉冲进行电气屏蔽。为便于计算,将Tpw等分为若干小区间,对(4)式进行离散化,以10 ps为步长且梯度递增的初始脉宽进行单时钟周期内的电路失效概率计算,则(4)式等价为:

(5)

其中,W为不同初始宽度的SET脉冲个数,求和项为传播到锁存器的SET脉冲被锁存的概率,其他参数与(3)式一致。

SER是器件或系统发生软错误的比率,其典型的评估指标是FIT(failure in time),即器件或系统在10×10内出现失效的次数[8]。以FIT表示的电路总体SER计算公式为:

(6)

其中,REH、RPH分别为辐射环境的粒子有效撞击率和粒子通量,取值[5]分别为2.2×10-5、56.5 m-2·s-1;Acomb为电路逻辑门单元面积总和。

算法2给出电路SER计算过程。算法首先读取输入参数,通过解析电路网表,得到各个门节点属性及其扇入扇出门链表;使用随机向量生成器产生N组输入向量,并分别将其施加到测试电路。对于每一组输入向量,进行如下操作:

(1) 使用仿真器得到逻辑门输入输出信号。

(2) 使用算法1查找各个逻辑门到锁存器的敏化路径,并记录敏化引脚延迟。

(3) 分别对每一条敏化路径上的第1个逻辑门进行不同初始宽度的SET脉冲注入,以模拟不同能量的粒子来袭,并将脉冲在敏化路径上传播;与此同时,使用(1)式进行电气屏蔽效应计算。

(4) 对到达锁存器的脉冲使用(2)式进行时窗屏蔽效应计算,得到各个脉冲造成的失效概率,并统计可得单时钟周期内的电路失效概率。最后通过(6)式计算得到电路总体SER。

算法2 SERComputing

∥输入：电路网表ckt、输入向量数N、门单元信息。

∥输出：电路总体SERSER。

读取输入参数；

解析电路网表ckt；

使用随机向量生成器产生N组输入向量；

fori←1 toNdo

电路逻辑仿真；

查找敏化路径并记录敏化引脚延迟；

forj←1 toSdo

forw←1 toWdo

fork←1 toMdo

使用式(1)进行电气屏蔽效应计算；

end

使用式(2)进行时窗屏蔽效应计算；

统计单时钟周期内的电路失效概率；

end

end

end

使用(6)式计算电路总体SERSER

3 实验与结果分析

为进一步验证本文方法的有效性,基于Nangate Open Cell 45nm工艺库对ISCAS’89基准电路的组合逻辑部分进行SER评估,并与同类文献进行比较和分析。实验环境为Windows XP OS、4GB RAM、Intel Quad-Core i5处理器,集成开发环境为Microsoft Visual Studio 2010,开发语言为C++。对于SET初始脉冲的生成,本文使用单指数电流源模型[5-6]进行模拟,即

(7)

其中,Q为入射粒子沉积电荷量;τ为脉冲波形时间常数。将电路工作频率设定为1 GHz,锁存窗大小设定为30 ps,Q设定为[10 fc,150 fc],τ设定为20 ps[5],随机产生5 000组输入向量,其他参数详见上文,针对ISCAS’89基准电路的SER评估结果与时间开销见表1所列。

表1 针对ISCAS’89基准电路的SER评估结果对比

定义A方法SER评估结果SERA相对于B方法SER评估结果SERB的评估偏差SERdiff为:

SERdiff=(SERA-SERB)/SERB

(8)

因此BFIT方法相对本文方法的SER评估偏差,其均值为8.2%。 其中,正偏差表示BFIT方法计算结果偏高,负偏差表示BFIT方法计算结果偏低,这是合理的。由1.1节可知,扇出重汇聚效应导致敏化路径条数既可能增多,也可能减少。敏化路径条数增多会导致SER评估结果偏高,而减少会导致评估结果偏低。针对表1中7组大规模基准电路,将本文方法与BFIT方法评估结果进行对比,如图3所示。由图3可以发现,2种方法的评估结果大体呈现一致的变化趋势,说明本文方法是合理的。

图3 本文方法与BFIT方法的SER评估结果

为进一步验证本文方法的准确性,将本文方法评估结果与基于蒙特卡洛方法的基准评估结果进行对比。蒙特卡洛方法使用晶体管级故障注入进行SER评估,计算精度高,但非常耗时。由(6)式可知,同一型号的电路在相同实验条件下,其SER与FP评估结果成正比关系,因此本文针对FP评估结果进行对比。以部分较小规模电路为例,将本文方法、BFIT方法和蒙特卡洛方法进行对比的结果如图4所示。

图4 不同方法的FP评估结果对比

由图4可知,本文方法与蒙特卡洛方法的FP评估结果较为接近。由于本文方法相对蒙特卡洛方法的平均评估偏差仅为1.5%,因此评估结果的正确性得到保证。但是,相比BFIT方法,本文方法虽然评估精度较高,但本文方法考虑了扇出重汇聚效应,因此引入了较多的时间开销。

4 结 论

本文提出一种考虑扇出重汇聚效应的组合电路SER评估方法。使用单指数电流源模型对由单粒子撞击组合逻辑门节点晶体管敏感区产生的SET脉冲进行模拟;分别使用提出的考虑扇出重汇聚的敏化路径逼近搜索算法、电气屏蔽和时窗屏蔽模型评估组合电路对SET脉冲的逻辑屏蔽、电气屏蔽和时窗屏蔽效应;对传播到锁存器的SET脉冲进行单时钟周期电路FP计算,进行通过提出的SER计算方法计算可得电路总体SER。实验结果验证了本文方法的有效性,因此能够为集成电路的选择性加固容错设计提供参考。

[1] FERLET CAVROIS V,MASSENGILL L W,GOUKER P.Single event transients in digital CMOS：a review[J].IEEE Transactions on Nuclear Science,2013,60(3):1767-1790.

[2] WU K C,MARCULESCU D.A low-cost,systematic methodology for soft error robustness of logic circuits[J].IEEE Transactions on Very Large Scale Integration Systems,2013,21(2):367-379.

[3] BLACK J D,DODD P E,WARREN K M.Physics of multiple-node charge collection and impacts on single-event characterization and soft error rate prediction[J].IEEE Transactions on Nuclear Science,2013,60(3):1836-1851.

[4] 韩健,梁华国,黄正峰,等.基于CVSL结构的组合逻辑选择性加固方案[J].合肥工业大学学报(自然科学版),2014,37(12):1468-1473.

[5] HOLCOMB D,LI W,SESHIA S A.Design as you see FIT:system-level soft error analysis of sequential circuits[C]//Proceedings of the Conference on Design,Automation and Test in Europe.Los Alamitos:IEEE Computer Society Press,2009:785-790.

[6] ZHANG M,SHANBHAG N R.Soft-error-rate-analysis(SERA) methodology[J].IEEE Transactions on Comuter-Aided Design of Integrated Circuits and Systems,2006,25(10):2140-2155.

[7] ZHANG B,WANG W S,Orshansky M.FASER:fast analysis of soft error susceptibility for cell-based designs[C]//Proceedings of the 7th International Symposium on Quality Electronic Design.Los Alamitos:IEEE Computer Society Press,2006:755-760.

[8] MISKOV-ZIVANOV N,MARCULESCU D.Modeling and optimization for soft-error reliability of sequential circuits[J].IEEE Transactions on Computer Aided Design of Integrated Circuits and Systems,2008,27(5):803-816.

[9] 陈书明,杜延康,刘必慰.一种基于混合模拟的计算组合电路中SER的方法与工具[J].国防科技大学学报,2012,34(4):153-157.

[10] 雷韶华,韩银和,李晓维.组合逻辑电路中SER的频域分析方法[J].计算机研究与发展,2011,48(3):535-544.

[11] 绳伟光,肖立伊,毛志刚.组合电路的SER自动分析平台[J].计算机辅助设计与图形学学报,2009,21(11):1661-1666.

[12] JIAO Jiajia,FU Yuzhuo.A heuristically mechanical model for accurate and fast soft error analysis[C]//Proceedings of the IEEE Asia Test Symposium,Los Alamitos:IEEE Computer Society Press,2014:33-38.

[13] LIU Biwei,CHEN Shuming,LIANG Bin,et al.The effect of re-convergence on SER estimation in combinational circuits[J].IEEE Transactions on Nuclear Science,2009,56(6):3122-3129.

[14] RAO R R,CHOPA K,BLAAUW D T,et al.Computing the soft error rate of a combinational logic circuit using parameterized descriptors[J].IEEE Transactions on Computer Aided Design of Integrated Circuits and Systems,2007,26(3):468-479.

(责任编辑 张 镅)

Re-convergence aware SER estimation for combinational logic circuits

YAN Aibin1,LIANG Huaguo2,XU Xiaolin2,YUAN Deran2

(1.School of Computer and Information, Hefei University of Technology, Hefei 230009, China; 2.School of Electronic Science and Applied Physics, Hefei University of Technology, Hefei 230009, China)

In order to accurately evaluate soft error rate(SER) of integrated circuits, a novel SER estimation technique for circuits was proposed. After gate-level logic simulation, by reversing the output signal of a particle striking gate cell, the sensitized paths and delay were accurately computed by the re-convergence aware sensitized path search algorithm under different input vectors. Then single event transient pulses were simulated by single-exponential current source model, and by propagating these pulses through the gate cells on sensitized paths respectively, electrical masking and timing masking were precisely evaluated by pulse masking models. Finally, SER of circuits was effectively calculated by the SER estimation technique. The experimental results show that the SER accuracy is improved by 8.2% on average via the proposed re-convergence aware SER estimation technique.

single event transient; logical masking; re-convergence; soft error rate(SER); failure probability

2015-08-27；

2015-11-11

国家自然科学基金资助项目(61274036;61371025;61474036;61574052)

闫爱斌(1983-),男,山东德州人,合肥工业大学博士生;

梁华国(1959-),男,安徽合肥人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2016.10.009

TN431.2;TP391.7

A

1003-5060(2016)10-1341-06