运用数形结合思想，设计课堂教学

吴定根

（安徽省芜湖市三园小学）

运用数形结合思想，设计课堂教学

吴定根

（安徽省芜湖市三园小学）

数形结合思想是数学重要的思想方法，新一轮课改教材进一步强化了这一思想方法。作为数学教师理应将这种数学思想方法渗透在相关内容的教学过程中，培养学生良好的数学素养与思维品质。

几何是数形的结合体。数与形如影随形，形是数的外在表现，而数是形的内在本质。数与形总是相辅相成的，既可“以形变数”，也可“以数化形”“形数互变”，数与形具有一定的对应性。

在一次数学活动课上，笔者以图为载体，通过一题多解，发散思维，训练学生数形结合的思想方法，培养他们的创新精神与探究能力。

一、找“朋友”，初步感知数形结合思想

用直线将下列可能相关的算式与图形连起来，并说出理由。

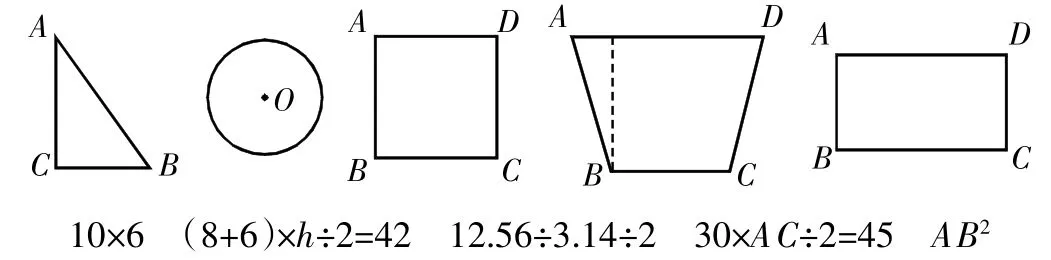
二、以形求数，用代数法解答

出示例题，“如图1，正方形ABCD的边长为4厘米，EF//BC，△CEH的面积为6平方厘米，求GF的长。”

先让学生同位或前后四人为一组，讨论解题策略。

如果用算术法解答，有一定的难度，先启发他们用代数法思考，尝试解答。

一生这样做：

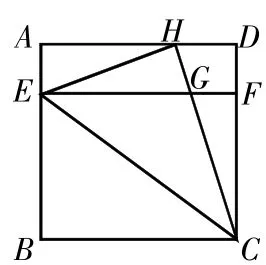
图1

设：△EGH的高为a厘米，△CEG的高为b厘米。所列代数式如下：

解得：EG=6×2÷4=3 GF=4-3=1。

另一生得到另一种结果：

设：△EGH的高为x厘米，面积为S平方厘米。所列代数式为：

还有一生是这样解答的：

设：△EGH的高为x厘米。列出代数式：

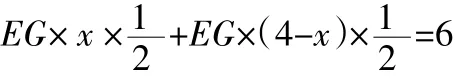
在集体评议时，大家一致认为前者和后者解答正确，而对第二种解法的评价是：“一个没有结果的算式”而已，甚至连解题者本人对这种做法也感觉莫名其妙，难以自圆其说。笔者首先肯定第二种解题方法求EG长也是可以的，它抓住了△EGH与△CEG共底的等量关系列式。再让大家将此解法的最后算式对照△EGH，分析算式“3×x×”表示的意义。学生理解了算式的含义，这才明白了算式中的“3”就是△EGH的底（EG的长），x是高，S= 3×x×是△EGH的面积计算，大家终于悟出了答案就隐藏在算式中。教师在此有意识地引导学生运用数形结合思想，将算式与图形（△EGH）作对照，强调数形的对应性。如果学生没有数形结合思想，就无法理解算式中的答案“3”。

因势利导，教者又进一步告知学生，几何图形的数与形总是相互依存的，往往有什么样的图形就会列出怎样的算式，而何种算式也可以折射它是一个什么样的图形，数与形就是这种形与影的关系。以上这三种解答方法都是由“形”求出“数”，特别是第二种解法，数形完全相符，即S=3×x×清楚地显示出△EGH的面积计算。

三、由数化形，用算术法解答

引导学生观察分析第一种解法最后的代数计算结果所呈现出的算术式：“6×2÷4=3”，第三种解法的最后解答结果所呈现的算术式：“6÷2=3”，将它们分别对照图1中的△CEH，看看这两种解答方法的数（算式）与形是否完全相符。经过一番思考与讨论，大家觉得这两种解法结果所呈现的算术式与图1均不相符。此刻，教师明确指出：在正常情况下，算式与图形总是相对应的。既然有这样的算式，就必然有与之相对应的图形，肯定可以通过“等积变形”的方法，达到图形与算式相一致，那就可以直接用算术方法解答了。

先观察第一种解法的算式GE=6×2÷4，分析算式的含义，让学生推想变形后的三角形应是面积为6平方厘米，底为4厘米，GE应该是高。

于是，让学生结合算式与图形的关系，动脑动手，尝试等积变形，用算术方法求EG。

几分钟后，有一组学生是这样做的（如图2）：

首先，连接AG、BG，得到△ABG。

因为，△AEG=△EGH（同底等高），△BEG=△CEG（同底等高）。

所以，△ABG=△CEH=6。这样，就把△CEH转化成△ABG，其面积依然为6平方厘米，底是正方形边长4厘米，EG是这个三角形的高。

因此，EG=6×2÷4=3，FG=4-3=1。

图2

充分肯定该组“等积变形”的研究成果，同时进一步强调算式与图形对应一致。再用上述方法猜想第三种解法EG=6÷2=3的对应图形，应怎样等积变形？学生很容易地说出，应该是一个面积为6平方厘米，宽为2厘米的长方形。

告诉学生，距离成功只有一步之遥了。只要能将△ABG转化成长方形，与上面的算式EG=6÷2=3相符合，鼓励学生在图2的基础上继续探究。

在距离下课时间只有几分钟的时候，终于有学生成功地解决了这个问题。

其解题思路为（如图3）：

作长方形ADFE的平分线XY，再作长方形BCFE的平分线JK，过G点作CD的平行线NM。将图3中的1移往2，将3移往4，正好拼成了一个宽为2厘米，面积为6平方厘米的长方形XPqJ，而EG相当于这个长方形的长。

所以，EG=6÷2=3，FG=4-3=1。

图3

这个学生的解答完全正确。在此基础上，教师再次引导学生印证代数法的最后算式EG=6÷2=3与推想出来的图3是否完全吻合。

教师小结：就这道题，我们由“形”列式求数，再由算式推想图形，数形相互转化，让我们用算术法又一次解决了问题。这种解题策略就是运用了“数形结合”思想。最后，屏幕上显示著名数学家华罗庚画像及其诗句，以“数形结合百般好，隔离分家万事休”的名句结束本节课。

运用数形结合思想，可将人们引入一个数学新天地，让人进一步领略数学的美妙与情趣，这对培养学生的创新思维具有积极作用。

张晓明.浅谈数形结合思想在小学数学中的应用［J］.学周刊，2014（33）.

·编辑 杨国蓉