基于可靠路径稳定性估计的MANET路由发现算法研究

李智楠，杨晓冬,2

（1. 哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨 150001；2. 日本明星大学联合研究中心，日本 东京 191-8506）

基于可靠路径稳定性估计的MANET路由发现算法研究

李智楠1，杨晓冬1,2

（1. 哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨 150001；2. 日本明星大学联合研究中心，日本 东京 191-8506）

提出一种基于可靠路径剩余生存期（RPL,residual path lifetime）估计的 MANET路由发现算法（RLE-RPLP），该算法充分考虑相邻链路剩余生存期相关性，建立优化的多跳路径 RPL统计特性分析，提供了更可靠的路由稳定性评估。通过仿真分别与忽略链路RLL相关性的源路由协议及已有稳定性路由协议进行对比。仿真结果表明，RLE-RPLP算法能有效提高网络吞吐量并减少路由重建次数；当节点移动度较高或网络负载较大时，在吞吐量、路由开销等方面均优于已有的稳定性路由对比算法。

移动ad hoc网络；链路剩余生存期；移动相关性；路径剩余生存期；稳定性估计

1 引言

移动ad hoc网络（MANET）摒弃了蜂窝网络昂贵的底层基站及相关基础设施建设，实现了移动节点分布式动态组网、自主处理的优越性能。节点间路径可靠性评估是决定MANET路由优化算法有效性及网络连通性的关键因素之一。由于MANET网络节点移动特性，多跳路径都具备一定的路径剩余生存期（RPL,residual path lifetime）[1]，即从路径建立或传输过程中某时刻至构成该路径的任一条链路初次发生中断的时间间隔。在主动式路由机制（proactive routing protocols）中，准确估计RPL可使算法在路径中断之前启动新的路径发现进程来保证节点间数据尤其是数据流业务的传输连续性；在反应式路由机制（reactive routing protocols）中，RPL的过高估计会导致路由算法频繁地启动路由修复或重建进程，降低网络通信质量，增加传输延时和资源消耗。因此，可靠的RPL估计是MANET路由机制优化和完善的关键因素。

文献[1～8]提出了基于可靠路径估计的路由策略。而作为多跳路径构成基础的链路剩余生存期（RLL,residual link lifetime）估计理论也得到深入探讨[9～13]。越来越多的路由优化策略及MANET现实应用[4,5,14]侧重于RLL统计特性[1,15,16]描述，但相邻链路 RLL相关性对路径稳定性评估的影响还没有得到足够重视。

文献[16]在文献[15]的基础上指出，路径生存期可以表示为各条链路生存期倒数之和，但两者均以链路独立性为前提。文献[1]将上述条件改进为一种渐进性条件，即RLL相关性会随路径跳数及平均链路长度的增加而减弱。然而以该理论为基础的RPL估计算法，并不适用于对路径跳数有严格限制的普遍情况。文献[4]提出了详细的链路及路径持续时间的理论分析模型，但推导设定所有节点移动速率相等且为常量，限制了理论实用性且很大程度上降低了相邻链路相关性约束。上述RPL预测的问题也同样存在于 ad hoc网络的实际扩展应用场景中，如VANET[5,17]、车联网系统（connected vehicles）[18]及航空通信网络[14,19]。文献[20]强调了 RLL相关性的重要意义并将其用于平均路径生存期估计 PDMP（piecewise deterministic Markov process）理论建模当中，然而离散的节点运动参数（速率和移动方向）必须作为满足数值分析的限制条件，同样不符合实际情况。

为了在路由机制中充分引入相邻链路 RLL相关性进而提供更准确的路径可靠性评估标准，本文首先提出了一种RLL相关性统计建模方法，在节点移动模型不受限的情况下给出多跳路径中各链路RLL联合概率密度分布（PDF）表达式，在此基础上提出一种基于可靠 RPL估计的路由发现算法（RLE-RPLP），该算法完善了路由发现进程中路径RPL的判断标准，因而能够减少路由失效频率。仿真分析将 RLE-RPLP与另外 2种路由算法进行对比，分别为忽略链路RLL相关性条件下的源路由协议及文献[19]提出的稳定性路由协议。通过性能对比验证了RLE-RPLP在提高网络吞吐量、减少路由重建次数及路由开销方面的有效性以及对基于路径稳定性路由算法的优化作用。

2 基于RLL相关性的RPL统计特性分析

由于节点共享，MANET同一路径中相邻链路RLL相关性是RPL估计的关键因素。文献[20]强调并验证了这一观点。本文提出一种链路RLL相关性统计建模方法，利用随机理论给出多跳路径中各链路RLL联合PDF明确表达式，该方法不以特定的节点移动模型为限制，为路径稳定性提供更可靠的评估参考。

首先构建简化路由模型，如图1(a)所示，并简要证明相邻链路RLL相关性。设节点N1、N2、N3构成 2条相邻链路 k1(N1−N2)、k2(N2−N3)。某时刻Ni移动速率Vi及方向θi任意。实际上链路RLL主要受限于其 2个端节点的剩余能量和两者相对距离，显然，若图1中仅N1或N3变化，k1和k2的RLL不会同时受到影响；而若k1和k2的共享节点N2能量消耗或随机移动，都会同时导致两者RLL发生变化，因此k1、k2的RLL的PDF相关性普遍存在。本文着重对节点随机移动引起的相邻链路 RLL相关性进行分析并应用于路由优化策略。

图1 子镜头分割流程

首先推导链路k1剩余生存期RLL1的PDF表达式。如图1所示，设R为节点传输半径，N2为坐标参考点，V2平行于正x轴。初始时刻（t=0）N1位置与N2距离为d1(d1＜R)，与负x轴夹角为α且α服从(0,2π)均匀分布(α～U(0,2π))。若某时刻t1，两节点间距首次超过R，则链路中断，RLL1=T1=t1。θ 为V1与V2夹角且θ～U(−π,π)；

显然，V1、V2、θ相互独立，有

其中，v1、ϑ分别代表随机变量 V1、θ某一特定取值（下同），V、φ分别表示N1、N2间相对速度及V与 x轴的夹角，φ∈(−π,π)。文献[19]中首先给出三维空间中2相邻节点相对速率的PDF表达式，进而推导出链路生存期的累积概率密度分布(CDF)和单条链路生存期期望值。上述推导均以V与φ相互独立为前提，而实际上两者存在统计相关性且不可忽略，证明如下：首先从直观上分析，根据图 1(b)显然可以看出，V取决于V1、V2，而φ与有关，因此必然与V有关，两者不可能是独立的。具体而言，利用图1中各参数几何关系可得

φ同样为V1、V2、θ的函数，且当三者取值范围变化时，函数对应关系也随之变化。为便于证明，讨论当 θ∈[0,π)∩ (V1cosθ −V2＞0)的情况（对应图 1（b）），此时有

由式(1)和式(2)可见，V1、V2、θ中任一参数发生变化均同时影响 V、φ取值，因此两者相互独立的假设并不成立。其次，考察V、φ相关系数

其中，Cov(·)和 Var(·)分别表示协方差和方差函数。利用仿真方法进行每组(v1,v2)采样点下10 000次随机实验，每次实验规定θ在(0,π)随机取值并求解式(3)，将所有实验结果的平均值作为各坐标点对应的相关系数。图2给出仿真结果，从图中可以直观看出，V、φ相关系数大多在0.5左右，这一结果有力证明了即使在V1、V2互不相关的条件下，V和φ的统计相关性依然存在且不可忽略。

图2 V和φ相关系数仿真结果

针对文献[19]中的问题，本文给出改进后的链路剩余生存期 PDF推导过程。首先设 F(·)为 CDF表达式，则引用文献[19]将表示为

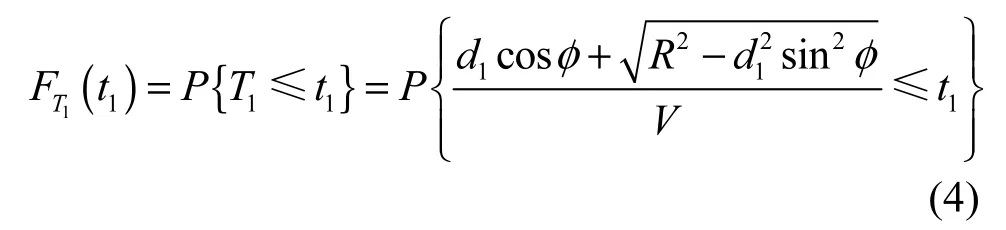
其中，P(·)为概率函数。当 V2为定值，V、φ均由V1和θ给定，有

其中，f(·)为 PDF函数。根据 Jacobian转换，可得如下条件PDF表达式

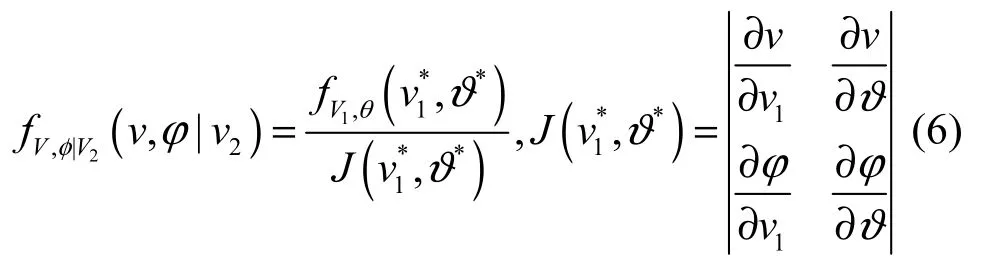
代入式(6)，可得

若假设 V1～U (Vmin,Vmax)，则有

代入式(5)并对t1求导，可得RLL1条件PDF表达式为

利用Leibniz法则将式(7)简化为一重积分，可得

进而可得RLL1的PDF表达式为

本文进一步给出考虑链路 RLL相关性的路径RPL统计分析。与式(8)推导方法类似，因此当V2取定值，k1和k2剩余生存期RLL1和RLL2的联合条件PDF表达式为

对 V2求积分，可得 RLL1及 RLL2的联合 PDF表达式为

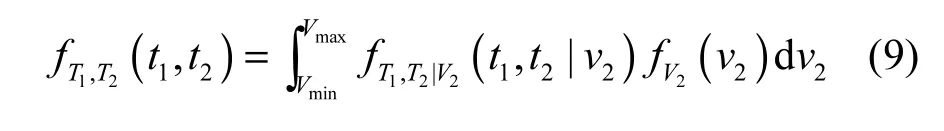
进一步地，若路径由3条链路构成，它们各自RLL的联合PDF可表示为

以此类推。

本文将路径统计特性进一步表示为多跳路径(l)的RPL不小于某一时间间隔T的概率，即路径中各链路RLL均不小于T的概率（Pl（T））。通过对式(9)或式(10)积分可得

3 RLE-RPLP路由算法设计

与主动式路由机制不同的是，反应式路由无需周期性地启动新旧路由替换来进行路由维护，节点间传输路径是按需建立的，节约了网络运行成本。AODV（ad hoc on-demand distance vector）和 DSR（dynamic source routing）是2种经典的反应式路由协议。本文首先根据上述理论建模提出一种以准确 RPL预测为标准的路由选取准则，接着以DSR协议为基础，给出RLE-RPLP算法实现及网络性能优化目标。

3.1 基于可靠RPL估计的路由稳定性准则

在路由发现进程中，目的节点Nd收到来自源节点Ns的路由请求RREQ报文之后沿原路径发送路由应答RREP报文。经典AODV协议中Ns只选取RREP最先到达的路径，DSR同样以“最短路径”准则进行路由选取，两者均无法保证路径稳定性。为了证明 RLE-RPLP路由策略在提供更准确路径RPL估计方面较以往算法的优越性，在引入和忽略相邻链路RLL相关性条件下，进行双链路RLL联合PDF仿真求解并给出误差分析。

首先在不考虑链路相关性时，式(9)可改写为

图3 RLL1、RLL2联合PDF数值仿真对比（R=100,d1=d2=50,Vd=10）

图3给出分别由式(9)和式(12)得到的RLL1和RLL2联合 PDF数值仿真对比结果。可见虽然两者变化趋势基本一致，但x-y平面各点所对应的联合PDF值存在显著差异，原点附近尤为明显（式(11)是式(9)所得结果的 4～5倍），而这一误差也直接影响Pl(T)求解结果。当改变(d1,d2)参数设置时，大量仿真对比结果证明：节点间初始距离越小，忽略RLL相关性导致的Pl(T)估计误差越大。因此，当链路长度较短，考虑RLL相关性会使RPL估计准确度提升更为明显。

3.2 RLE-RPLP算法实现

RLE-RPLP路由发现算法采用与DSR相似的源路由机制，源节点保存完整路由并提供多路径支持，具体实现过程如下。

路由请求。当有数据请求到达，Ns以广播形式向邻居节点发送RREQ报文，报文格式如图4(a)所示。除了 Ns、Nd地址及路由表等基本信息，RLE-RPLP算法的RREQ中还需要包含路径选取所需的节点移动参数，该参数随RREQ转发实现获取，详细记录了路由表中各节点所遵循的随机移动模型以及与其上游节点的相对运动信息，并按照不同的分组与各节点对应。

路由决策。Nd接收到来自同一数据请求的首个RREQ时启动延时定时器，进入路由选取阶段。具体算法实现见算法 1。Nd首先在定时器规定时间内根据RREQ携带的路径信息选取多条链路不相交（link-disjoint）路径，构成备用路径集合{l}，再利用各路径的节点移动参数，根据式(11)或其推广形式计算{l}中路径 RPL不小于预设时间间隔T的概率Pl(T)（T应大于待传数据的预期传输时间Te）。设Pth为RLE-RPLP算法预设的稳定性阈值，最终满足Pl(T)≥Pth且跳数最少的路径将被选为最终路由。

路由应答。路由决策完成后（与路由选取定时器数值归零基本同步），Nd将所选路径信息保存于RREP报文中并沿该路径发送至Ns。RLE-RPLP算法的RREP报文格式如图4(b)所示。

图4 RLE-RPLP算法路由控制报文格式

算法1目的节点处路由选取

描述：目的节点Nd接收到其上游节点Np发送的RREQ报文，报文中携带路径l的相关信息。

1)if （RREQ生存期值归零）or（l与Nd已记录的具有相同lt;Ns地址,广播ID＞的某条路径重合）

2)丢弃该RREQ报文

3)else 将Nd添加到RREQ路由表中

4)if （l为其lt; Ns地址,广播 ID ＞对应的第一条路径）

5)添加l至备选路径集合{ }

6)启动该lt; Ns地址,广播ID ＞路径选取定时器Timer

7)else if （l与Nd中已有的含相同lt; Ns地址，广播ID ＞的路径均严格不相交）and（Timer未归零）

8)添加l至备选路径集合{ }

9)else丢弃该RREQ报文

10)end all if

11)when (Timer==0)

12)find Pl(T)≥Pth且跳数最少的路径

13)设置该路径为 RLE-RPLP算法最终路由

3.3 网络性能优化目标

本文以吞吐量（Th，单位时间内网络成功传输的数据量），路由重建次数Nr及路由开销作为评价标准来验证 RLE-RPLP在提高网络性能方面的优势。Nr表示一定时间内所有用于数据传输的路径由于链路断裂需要重建的次数；路由开销是指 Ns与Nd间完成一次数据传输需要交换的路由控制报文主要为RREQ和RREP数量。Th实际上由网络中各层协议共同决定。本文为了强调路径稳定性对Th的影响，作如下定义及说明。

定义1Pls( T)表示路径ls在间隔T内传输数据被目的节点正确接收的概率。若ls由Q条链路构成，t1,t2,…,tq分别表示各链路RLL，则根据式(11)有

式(13)实质上从网络层角度量化了路径在所需时间间隔内成功完成数据传输的能力。文献[21]通过定义链路成功传输概率 pi,j来描述物理层干扰对链路的影响，因此本文定义1作为pi,j定义的延伸，旨在描述网络层路由机制中路径稳定性对端到端数据传输的整体影响，具有合理性。

定义 2若只考虑路径跳数较少的情况，可以假设备选路径传输Fs（packets）所需时间T0(s)大致相等，若Fs为Ns到Nd单次传输请求所含数据量，N为T0内网络数据传输路径总数，则吞吐量定义为

式(14)未考虑物理层和 MAC层影响，即忽略物理层信号衰落并假设 Nd对接收数据都能正确解码且无重复或乱序。由于本文研究MANET网络层路由协议优化，因此上述简化不影响算法评估有效性及其可扩展性。

接下来，利用图 5(a)中简化网络模型将 RLERPLP路由选取方法与“最短路径”准则进行对比，给出算法优化例证。设Fs从Ns到Nd的传输需在T0内完成，A、B、C分别表示3个中间节点，Nd在路由选取结束后共得到l1(Ns→A→Nd)和l2(Ns→ B→C→Nd)2条备选路径信息。图5(b)给出本文算法和忽略RLL相关性时两者Pl(T0)值，即P1，P2分别代表数据成功接收概率的实际（准确）估值和过高（错误）估值。

设路径稳定性阈值Pth=0.7，Fs和T0归一化为1。本文算法参考P1，只有l2达到标准，由式(14)得到网络吞吐量为0.8；若不考虑链路RLL相关性（P2为参考），l1和l2均达到稳定性标准，最终跳数较少的l1被选为最终路由。但Th计算需要用数据成功接收概率的实际值P1，因此Th仅为0.6。由此可见RLE-RPLP算法能够避免RPL估计误差造成的路径稳定性误判，优化了网络性能。

图5 RLE-RPLP优化性例证简化网络模型及路径稳定性设置

4 网络性能仿真分析

为了验证RLE-RPLP算法合理性及有效性，进行MATLAB仿真环境下的MANET网络构建，路由机制实现及性能对比分析。MATLAB广泛应用于路由算法仿真中，并且能够对单层协议设计提供可信度较高的性能分析及合理性验证[22～24]。本文利用两组参数设置将 RLE-RPLP算法分别与忽略链路RLL相关性条件下的源路由协议及文献[19]中提出的稳定性路由协议进行对比并给出仿真结果及性能分析。

4.1 引入RLL相关性的路由机制优化作用

对比算法与本文算法路由发现进程类似，但区别在于：路径稳定性评估不考虑RLL相关性，Pl(T)利用式(12)及其推广形式计算。采用Th和 Nr作为性能指标对两者进行对比分析。

4.1.1 网络参数设置

设移动节点随机分布于100 m×100 m的方形区域，各节点带宽足够大（无链路拥塞延迟），每个仿真周期T0=5时隙起始时刻加载N个(N=10)Ns不同且大小为Fs(25单元)的数据流服务请求，数据预期传输时长为T0，R=20 m，Pth=0.8，路径选取定时器=0.05 T0，Pl(T)计算中取 T=1.5 T0。仿真共运行100 T0。速率和吞吐量单位分别设为米/时隙、单位/时隙。

定义路由重建（失效）条件：1)RLE-RPLP算法，路由发现进程中备选路径Pl(T)值均未达到Pth；2)对比算法，所选路径实际Pl(T)值未达到Pth（因该算法会导致 Pl(T)估计过高，因此当参数设置合理，每个数据请求备选路径中至少有一条路径满足Pl(T)≥Pth）。若发生路由重建，则 Th 计算时（式(14)）对应路径Pl(T)值为0，即认为数据不允许重传，一旦路径失效，则数据丢失。

4.1.2 结果与分析

图6和图7分别给出当Vd=10，Th和Nr随网络节点数（Np）变化的仿真对比结果。由图6可见，Th随Np增加（节点密度增大）呈上升趋势。当Vmin=2，RLE-RPLP算法所得Th比不考虑RLL相关性的结果平均提升约16%。其根本原因在于：忽略链路相关性使路径Pl(T)估计值偏高，达到Pth要求的备选路径数量增多，路由选取时可靠性最佳的路径很容易被“跳数最少”路径所替代，导致数据丢失频率增加，降低网络吞吐量。其次，当 Np=20和70，2种算法所得Th差值分别为3和8，说明RLE-RPLP对吞吐量优化效果随 Np增大而增加。这一结果的理论依据在于：Np越大，链路平均长度越短，2种算法Pl(T)计算值相差越大，以RPL估计准确度占优的RLE-RPLP算法能获得更理想的Th。另外，当节点移动度增大（Vmin由2增加到5，Vd不变），Th均有所下降，但Vmin=5时，RLE-RPLP算法所得 Th依然优于对比算法在Vmin=2时的结果，说明本文算法能够有效缓解因节点移动性增加而造成的网络性能恶化。

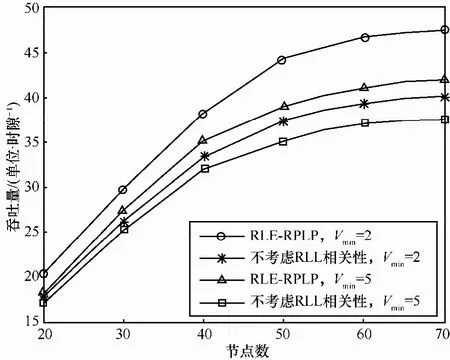
图6 Np变化时Th仿真结果对比（Vd=10）

图7 Np变化时Nr仿真结果对比（Vd=10）

图7同样表明增加节点密度能够提高网络连通性，实现性能提升（Nr减少）。仿真结果显示，RLE-RPLP算法能有效降低路由重建次数，且节点移动度较高时效果更为明显。以Np=70处仿真结果为例：Vmin=2时，RLE-RPLP的Nr值较其对比算法减少约53%；而Vmin=5时，这一比率上升至71%。另外，对比Np=70处Vmin分别为2和5的结果，可见忽略 RLL相关性时 Nr差值为 21；而运用RLE-RPLP算法Nr差值仅为3，进一步验证了其在高节点移动度下保证网络性能的能力。

图8和图9分别给出当Vmin=2，Th和Nr随节点移动度(Vd)变化的仿真对比结果。显然Vd增大加剧了网络拓扑的动态变化，使链路断裂的概率增大，网络性能有所降低。而RLE-RPLP在这种情况下依然表现出明显的优越性：当 Np=60，图 9中RLE-RPLP算法Th较对比算法提升约20%；图10中前者Nr较后者减少约57%。当Np=40，网络性能整体偏低，与图6和图7所得结论一致。

图8 Vd变化时Th仿真结果对比（Vmin=2）

图9 Vd变化时Nr仿真结果对比（Vmin=2）

4.2 与已有稳定性路由协议性能对比

进一步将RLE-RPLP算法与文献[19]提出的基于链路有效性估计的路由（LEBR,link availability estimation based routing）算法进行比较，以吞吐量和路由开销作为性能指标实现有效性验证。LEBR算法以链路生存期作为其有效性量化标准，主要特点为：1)以AODV协议为改进基础，同一路径中的各节点只保存了其相邻节点路由信息，各链路有效性(Lij)需随RREP转发逐跳计算；2)路径有效性(PLA)为各链路 Lij的乘积，即 PLA=∏ Lij。由此可见，LEBR强调链路级别的稳定性分析，且默认各链路统计特性相互独立。

4.2.1 网络参数设置

各参数设置如表1所示。与文献[19]不同，仿真中采用简化的节点随机移动模型，节点速率服从最大值与最小值间的均匀分布特性。LEBR算法采用改进的AODV协议实现，即在对应RREP报文及路由表中加入PLA分区用于有效性指示及路由选取。

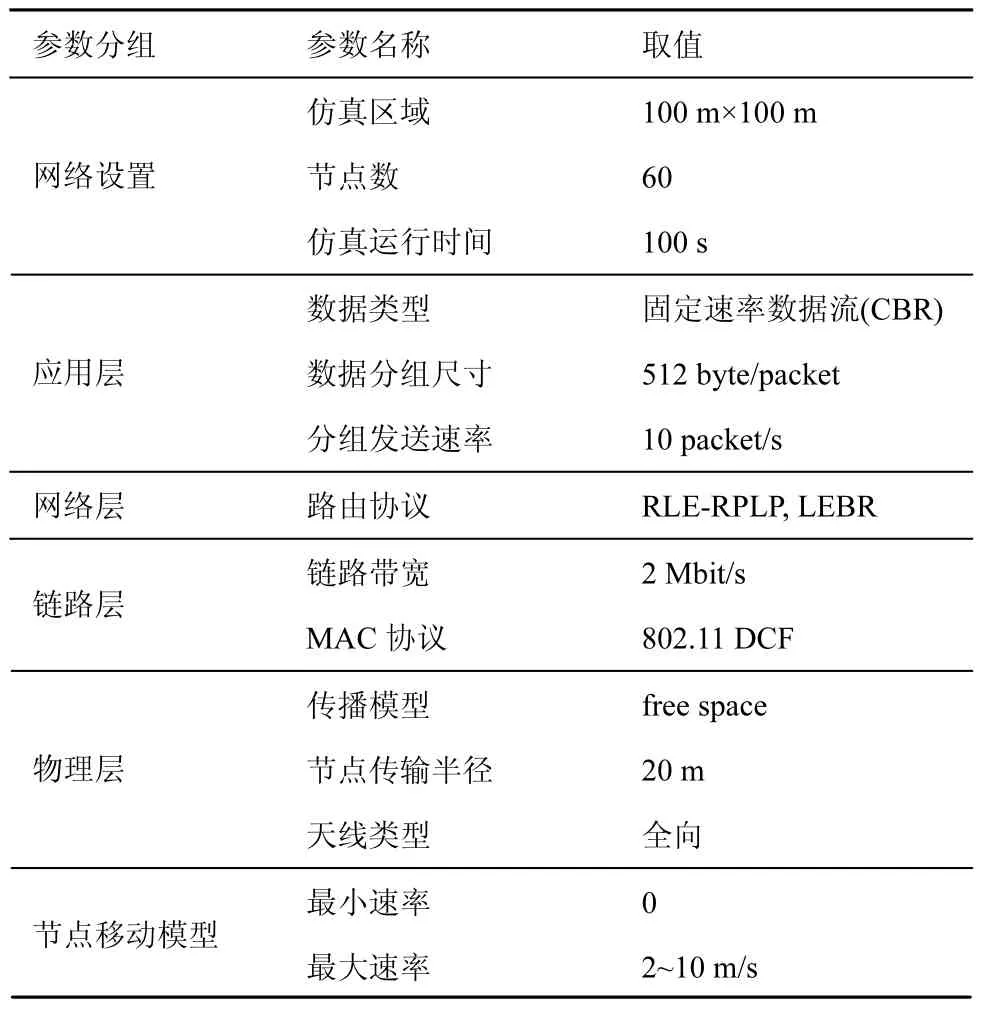
表1 仿真参数设置

4.2.2 结果与分析

图10和图11分别为当网络加载的数据请求数量Nq为10，2种算法在节点移动度（Vmax）变化情况下所得Th及路由开销对比结果。如图10所示，当移动度相对较低（Vmax不大于 6），两者所得 Th基本一致（大于 7×104bit/s），而当 Vmax=10，RLE-RPLP算法Th（约4×104bit/s）约为LEBR算法Th（约2.4×104bit/s）的1.6倍，说明本文算法在Vmax较大时能够保证较低的 Th下降速率，显示出了在对抗网络高度动态性方面的优势。图 11进一步验证了 RLE-RPLP算法的这一优势：当6≤Vmax≤10，RLE-RPLP算法路由开销比LEBR算法降低了约26%。其原因为：在节点高速运动使路径稳定性明显下降的情况下，本文算法能够以路径整体生存期估计作为参考依据进行更可靠地路由决策，有效地减少了因路由重建而产生的RREQ泛洪概率，从而降低了路由开销。

图10 Vmax变化时Th仿真结果对比(Nq=10)

图11 Vmax变化时路由开销仿真结果对比(Nq=10)

图12和图13分别为Vmax=8情况下，网络中数据传输请求数量变化时2种算法所得Th及路由开销对比结果。由图12可知，两者Th差值随数据请求增加而增大：当Nq=1，两者Th几乎相等；当Nq=20，本文算法Th（约6.5×104bit/s）比LEBR算法Th（约4.3×104bit/s）提升约51%。实际上，当Nq增加，网络中物理层及链路层的数据通信质量会受到影响，路由选择机会相应减少，相比LEBR算法中逐跳的链路有效性判断，RLE-RPLP算法中基于路径RPL的路由决策准则能够更有效、真实地评估所选路径的稳定性进而保证其持续连通性。从图 13结果来看，RLE-RPLP算法在所有Nq对应值情况下都能更有效地控制路由开销：较LEBR算法平均减少约17%，当 Nq较大时尤为明显（当 Nq=20，这一比率约为21.6%）。这一结果同样验证了本文算法在可靠路径稳定性判断中的优化效果以及对网络性能的提升作用。

图12 Nq变化时Th仿真结果对比（Vmax=8）

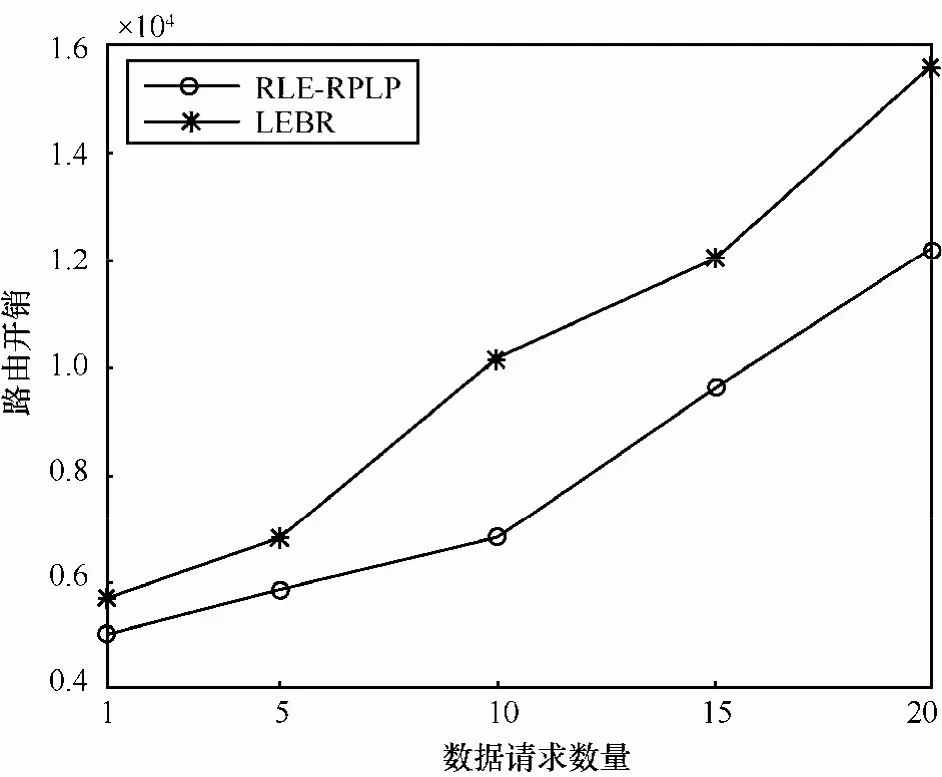
图13 Nq变化时路由开销仿真结果对比（Vmax=8）

5 结束语

本文将MANET多跳路径中相邻链路RLL相关性引入路径RPL统计特性分析，重点研究更具一般性及实际意义的路径稳定性估计准则，提出了一种基于可靠路径 RPL估计的路由发现算法（RLE-RPLP）。该算法首先通过相邻链路 RLL相关性统计建模，给出了在节点移动模型不受限情况下多跳路径中各链路RLL联合PDF表达式及理论推导过程，进而优化了路径RPL的统计特性描述，建立了更准确的路由稳定性判断准则，在此基础上提出了优化的RLE-RPLP路由发现算法。仿真分析表明：在路径跳数较少、链路长度较小的一般性MANET环境中，该算法与不考虑RLL相关性的稳定性路由算法相比，在提高网络吞吐量、减少路由重建次数方面具有显著优越性；与基于链路有效性估计的LEBR算法相比，能够在节点移动度较高或网络负载较大时更有效地保证网络吞吐量及控制路由开销，对网络性能具有更明显的优化作用。

[1]LA R J,HAN Y. Distribution of path durations in mobile ad hoc networks and path selection[J]. IEEE/ACM Transactions on Networking,2007,15(5):993-1006.

[2]王博,陈训逊. ad hoc网络中一种基于信任模型的机会路由算法[J]通信学报,2013,34(9): 92-104.WANG B,CHEN X X. Opportunistic routing algorithm based on trust model for ad hoc network[J]. Journal on Communications,2013,34(9):92-104.

[3]VU T K,KWON S. Mobility assisted on demand routing algorithm for MANETs in the presence of location errors[J]. The Scientific World Journal,2014,Article ID 790103.

[4]NAMUDURI K,PENDSE R. Analytical estimation of path duration in mobile ad hoc networks[J]. IEEE Sensors Journal,2012,12(6): 1828-1835.

[5]NAMUDURI K,WAN Y,GOMATHISANKARAN M,et al. Airborne network: a cyber-physical system perspective[C]//The first ACM MobiHoc workshop on Airborne Networks and Communications. c2012:55-59.

[6]YANG W,YANG X,YANG S,et al. A greedy-based stable multi-path routing protocol in mobile ad hoc networks[J]. Ad Hoc Networks,2011,9(4): 662-674.

[7]SARGOLZAEY H,ALI B M,KHATUN S. A cross layer metric for discovering reliable routes in mobile ad hoc networks[J]. Wireless Personal Communications,2012,66(1): 207-216.

[8]居熙,陶军,陆一飞,等. 一种基于迁移可测度的移动自组织网络路由模型[J]. 电子学报,2010,38(6): 1-5.JU X,TAO J,LU Y F,et al. A predictable-delivery-ratio based routing model in mobile ad hoc networks[J]. Acta Electronical Sinica,2010,38(6): 1-5.

[9]HUA E Y,HAAS Z J. An algorithm for prediction of link lifetime in MANET based on unscented kalman filter[J]. IEEE Communications Letters,2009,13(10):782-784.

[10]HAAS Z J,HUA E Y. Residual link lifetime prediction with limited information input in mobile ad hoc networks[C]// The 27th IEEE International Conference on Computer Communications. c2008: 13-18.

[12]CARMO R D,WEMER M,HOLLICK M. Signs of a bad neighborhood: a lightweight metric for anomaly detection in mobile ad hoc networks[C]//8th ACM Symposium on QoS and Security for Wireless and Mobile Networks. c2012: 47-54.

[13]WANG C F,CHIOU Y P,LIAW G H. Next hop selection mechanism for nodes with heterogeneous transmission range in Vanets[J]. Computer Communications,2015,55: 22-31.

[14]VIRIYASITAVAT W,BAI F,TONGUZ O K. Dynamics of network connectivity in urban vehicular networks[J]. IEEE Journal on Selected Areas in Communications,2011,29(3): 515-533.

[15]SADAGOPAN N,BAI F,KRISHNAMACHARI B,et al. PATHS:analysis of path duration statistics and their impact on reactive MANET routing protocols[C]//The 4th ACM International Symposium on Mobile Ad Hoc Networking and Computing. c2003: 1-3.

[16]HAN Y,LA R J,MAKOWSKI A M,et al. Distribution of path durations in mobile ad hoc networks-Palm’s theorem to the rescue[J].Computer Networks,2006,50(12): 1887-1900.

[17]KARAGIANNIS G,ALTINTAS O,EKICI E,et al. Vehicular networking: a survey and tutorial on requirements,architectures,challenges,standards and solutions[J]. IEEE Communications Surveys and Tutorials,2011,13(4): 584-616.

[18]LU N,CHENG N,ZHANG N,et al. Connected vehicles: solutions and challenges[J]. IEEE Internet Things Journal,2014,1(4): 289-299.

[19]LEI L,WANG D,ZHOU L,et al. Link availability estimation based reliable routing for aeronautical ad hoc networks[J]. Ad Hoc Networks,2014,20: 53-63.

[20]ANTUNES N,JACINTO G,PACHECO A. An analytical framework to infer multihop path reliability in MANETs[C]//The ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Systems. c2010: 323-332.

[21]LEE G Y,HAAS Z J. Simple,practical,and effective opportunistic routing for short-haul multi-hop wireless networks[J]. IEEE Transactions on Wireless Communications,2011,10(11): 3583-3588.

[22]DANA A,ZADEH A K,SADAT NOORI S A. Backup path set selection in ad hoc wireless network using link expiration time[J]. Computers and Electrical Engineering,2008,34(6): 503-519.

[23]WU Y S,LEE D H,JUNG J I. Derivation and analysis of link/route maintenance probability in multi hop mobile ad hoc networks[C]// International Conference on Information Technology: New Generations.c2009: 623-627.

[24]SHELLY S,VIJAY V,BABU A V. Model for path duration in vehicular ad hoc networks under greedy forwarding strategy[C]// International Conference on Computer,Communication and Convergence(ICCC 2014). c2014: 394-400.

Routing discovery algorithm based on reliable path stability estimation in MANET

LI Zhi-nan1,YANG Xiao-dong1,2

(1. College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China;2. Collaborative Research Center,Meisei University,Tokyo 191-8506,Japan)

A novel routing discovery algorithm for MANETs was proposed based on reliable residual path lifetime (RPL)prediction (RLE-RPLP). Correlation between residual link lifetime (RLL)of neighboring links was explicitly investigated and fully taken into account in stability estimation of multi-hop paths in the algorithm. Optimized RPL statistical properties were further explored to offer a more reliable path stability metric. Simulation analysis demonstrates that the proposed RLE-RPLP routing discovery algorithm shows prominent superiority in improving network throughput and reducing route reconstruction frequency. Moreover,compared with the existing link stability-aware routing protocol,the RLE-RPLP achieves better performance improvement in terms of throughput and routing overhead.

MANET,residual link lifetime,mobility correlation,residual path lifetime,stability estimation

signal strength based link lifetime estimating mechanism in MANET[C]//IEEE Conference An-thology. c2013: 14.

TN929.5

A

2015-12-21；

2016-06-21

10.11959/j.issn.1000-436x.2016162

李智楠（1987-），女，辽宁丹东人，哈尔滨工程大学博士生，主要研究方向为无线通信系统理论、MANET路由优化算法等。

杨晓冬（1963-），男，黑龙江哈尔滨人，博士，哈尔滨工程大学教授，主要研究方向为现代通信系统技术与理论、现代天线技术等。