基于DTW的长期直觉模糊时间序列预测模型

范晓诗，雷英杰，路艳丽，王亚男

（空军工程大学防空反导学院，陕西 西安 710051）

基于DTW的长期直觉模糊时间序列预测模型

范晓诗，雷英杰，路艳丽，王亚男

（空军工程大学防空反导学院，陕西 西安 710051）

针对现有直觉模糊时间序列模型中直觉模糊关系组和确定性转换规则过度依赖训练数据规模的问题，提出一种基于动态时间弯曲（DTW,dynamic time warping）距离的长期直觉模糊时间序列预测模型。通过直觉模糊C均值（IFCM,intuitionistic fuzzy C mean）聚类构建直觉模糊时间序列片段库，动态更新和维护规则库，减少系统复杂度。提出基于DTW距离的直觉模糊时间序列片段相似度计算方法，有效解决不等长时间序列片段匹配问题。通过对合成数据以及包含不同时间序列模式的气温数据的实验，与其他相关模型比较，说明该模型对于不同时间序列趋势变化模式中均具有较高的预测能力，克服传统模型提高模型只能满足单一模式时间序列预测，提高模型的泛化性能。

DTW；直觉模糊集合；IFCM聚类；时间序列；预测

1 引言

由于对模糊数据和不确定性信息处理的优势，模糊时间序列（FTS,fuzzy time series）分析理论的提出[1]得到了广泛关注和研究。大量优化理论与其进行了有效融合，文献[2]构建了基于粒子群的混合模糊时间序列模型;文献[3,4]利用信息粒对模糊区间进行划分，提高模型预测精度；文献[5]结合蚁群与自回归算法进行模型优化；文献[6]提出基于C均值聚类及神经网络的混合预测模型。相关文献对模糊时间序列模型的多元和高阶问题进行了研究[7～9]。随着 FTS理论的不断发展，单一隶属度的模糊度量存在一定局限性，文献[10]将直觉模糊集引入模糊时间序列模型，提出直觉模糊时间序列（IFTS,intuitionistic fuzzy time series）。

随后，一些学者对直觉模糊时间序列预测问题进行了深入研究，文献[11]初步给出直觉模糊时间序列建模方法；文献[12]提出基于概率及直觉模糊的时间序列模型；文献[13]提出参数自适应的直觉模糊C均值聚类的IFTS模型；文献[14]和文献[15]分别将矢量量化与确定性转换与直觉模糊时间序列结合，进一步优化预测模型。由此可见，直觉模糊时间序列成为模糊时间序列的重要发展方向。

时间序列分析研究序列数据的关联性，通过历史数据挖掘序列变化规律，用以完成对未来数据的预测工作。传统模型侧重于短期、单值预测，模型应用范围有限，文献[16]将短期模糊时间序列拓展到长期范围，构建了多值输出预测模型，文献[13,15]在此基础上改进并提出直觉模糊长期预测模型；文献[17]利用直觉模糊最小二乘支持向量机进行长期经济周期预测。然而，长期模糊时间序列预测理论研究相对较少，没有统一的评价标准，文献[15,16]将长期定义为多个输出值，并没有准确反映出序列数据变化趋势。传统模糊时间序列构建匹配规则库,极大地增加系统复杂度，如文献[7,8]构建的模糊逻辑关系组，文献[15,16]构建的确定性转换规则库，其本质上均是通过历史序列数据建立一定推理规则，通过搜索匹配项或相似匹配项，从而得到输出结果。这些模型极其依赖训练数据集的规则库，如果没有动态维护原有规则库，当出现匹配度较低的时间序列片段时，模型预测准确度将大大降低；如果实时更新规则库，则系统开销随数据规模增大而增大。因此，本文提出一个更加合理的长期直觉模糊时间序列模型，利用DTW距离有效解决非等长直觉模糊时间序列匹配问题，同时动态更新和维护时间序列库，避免规则库随预测范围的变化而增长，减少系统复杂度，最后通过实验证明该模型的有效性。

2 基础理论

定义 1(直觉模糊时间序列)假设{Y(t),t=0,1,…,n}是论域U上的一个时间序列，A是U上的一个划分，即其中，Ai是语言变量值。如果在{Ai}上相对于Y(t)的直觉模糊集F(t)有隶属度和非隶属度的函数对其中，且那么FI(t)被称为一个定义在在Y(t)上的直觉模糊时间序列，表示为

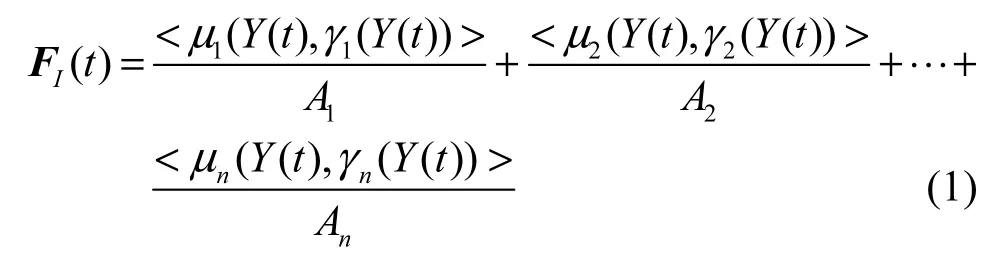
其中，“+”表示连接符。

定义 2(直觉模糊时间序列关系)对于一个直觉模糊时间序列FI(t)，如果仅由前一时刻FI(t−1)决定，称之为一阶时间序列，表示为其中，“◦”表示直觉模糊合成操作算子，RI(t,t−1)表示直觉模糊关系矩阵，并且如果FI(t)的隶属度函数与非隶属度函数分别为那么隶属度和非隶属度关系矩阵如式(2)所示。

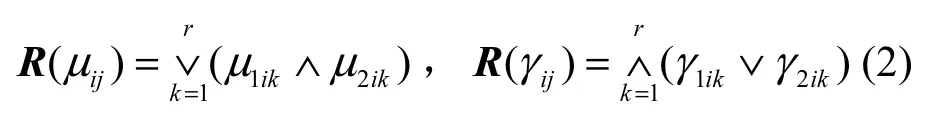
如果FI(t)由前m个值FI(t−1),FI(t−2),… ,FI(t−m)决定，称FI(t)为m阶直觉模糊时间序列，关系表达式如式(3)所示，其中，“×”是笛卡尔乘积。

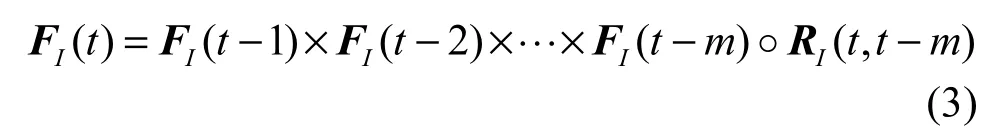
定义3(动态时间弯曲距离)给定长度为n和m的2个时间序列A和B，分别记为A=a1,a2,…,an,B=b1,b2,…,bm，构造一个n×m的弯曲矩阵，如图1所示，其中任意位置表示ai到bj的距离d(ai,bj)，定义弯曲矩阵上长度为 K的弯曲路径 Wn,m=(w1,w2,…,wk,…,wK)，其中，wk=(i,j)k表示弯曲路径上第k个元素，并且

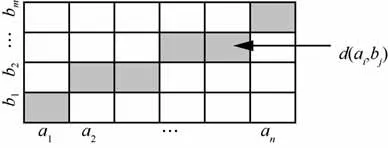
图1 DTW弯曲矩阵与弯曲路径

弯曲路径应满足以下条件。

1)边界条件：路径起始点为(a1,b1)，终止点为(an,bm),即时间序列端点对齐。

由此定义时间序列点对基距离之和的最小值为 DTW 距离，如式(4)所示，DTW 距离对应的弯曲路径为最佳路径。

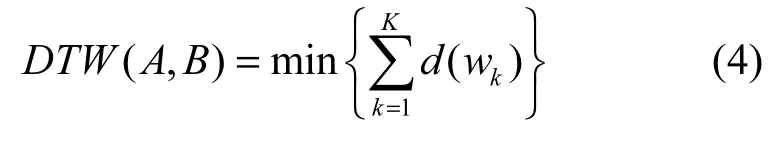
求解最佳路径通常构造一个 n×m的距离矩阵DDTW，其中每个元素表示A(a1,aj)到B(b1,bi)的DTW距离，定义为

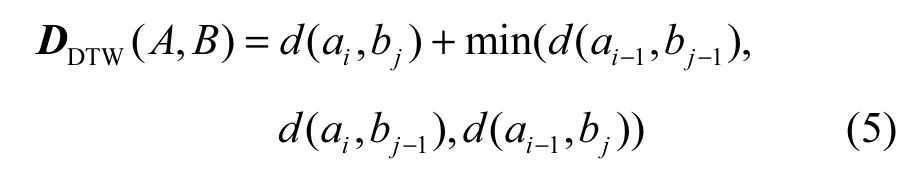
3 长期直觉模糊时间序列

本文提出一个基于 DTW 距离的长期直觉模糊时间序列预测模型，通过IFMC聚类算法从训练数据中提取时间序列片段并生成匹配规则库，同时校正和更新规则库，从而降低传统模型的系统复杂度，提高预测准确度。模型基本框架如图2所示。

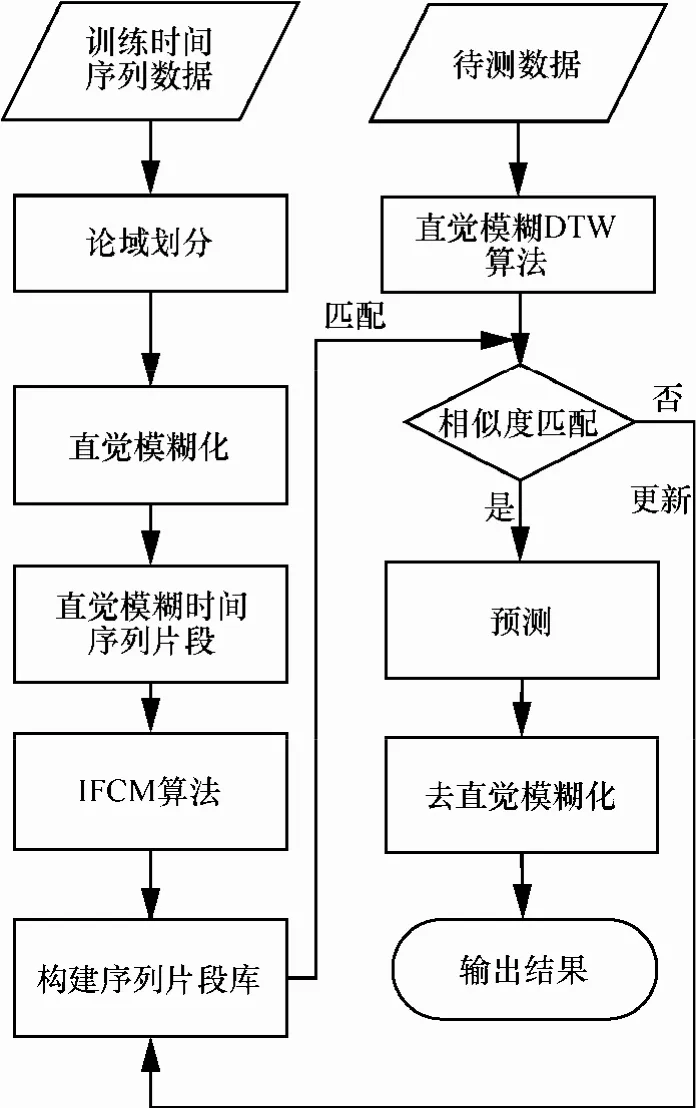
图2 基于DTW的长期IFTS预测模型

3.1 直觉模糊时间序列

直觉模糊时间序列是对模糊时间序列的扩展和延伸，其基本结构包括论域的划分、数据的直觉模糊化、模糊推理关系或预测规则库的构建以及预测算法。本文模型首先对数据进行直觉模糊化和论域划分，定义全局论域其中，Dmin和Dmax分别表示最大和最小训练数据，Ai表示语言变量且其中，μj和

jγ由式(6)计算得出，分别表示Ai属于ui的隶属度和非隶属度函数。n表示论域划分区间数量，dj表示区间边界，xi为历史数据，λ表示直觉模糊调节因子。因此，根据数据所在划分区间，可以得到模糊语言值，最后依据式(1)得到一个直觉模糊时间序列Fi(t)。

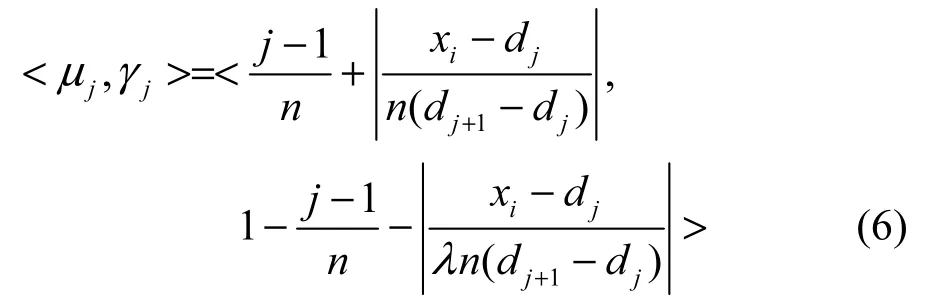
相应地，当需要输出精确结果时，根据式(7)对直觉模糊预测结果进行去模糊化。

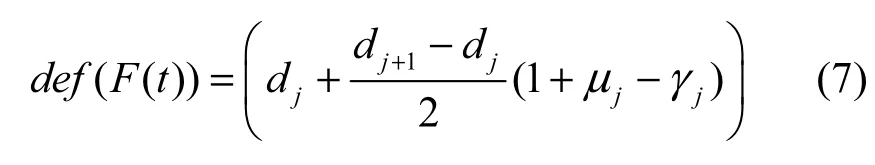
3.2 构建时间序列片段

时间序列预测模型，通常通过挖掘序列数据变化趋势，构建相应规则库作为预测基础。文献[7,8,12]根据历史数据构建模糊推理关系组，预测算法通过搜索匹配的模糊关系得到输出结果，这种方法预测精度高，但需要构建大量模糊推理关系组，系统复杂度随数据规模增大而增大，不便于维护；文献[15,16]构建确定性转化规则库作为预测依据，预测算法依赖时间序列状态确定性转化，当出现不确定性转化时，需要进行大量递归回溯，算法复杂度依然较高，同时对于模糊时间序列变化趋势反映不够明显，当没有出现匹配规则时，预测精度大大降低。因此，这些模糊时间序列预测模型的泛化性能不够理想，不适用于长期时间序列预测问题。因此，本文利用直觉模糊C均值聚类算法(IFCM)结合 DTW 算法建立和更新时间序列片段库，使其满足长期预测跟踪匹配，有效降低技术复杂度。

IFCM算法通过目标函数Je最小化原则，将数据集X=(x1,x2,…,xn)划分为C类[11]，表示为

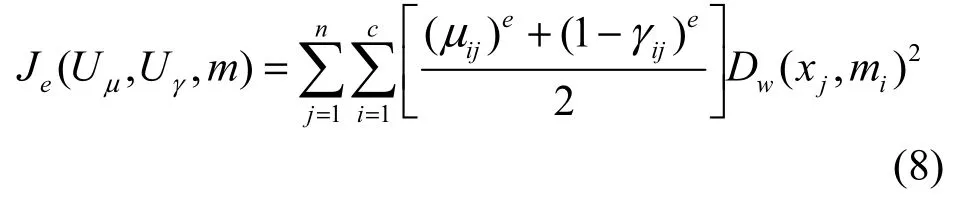
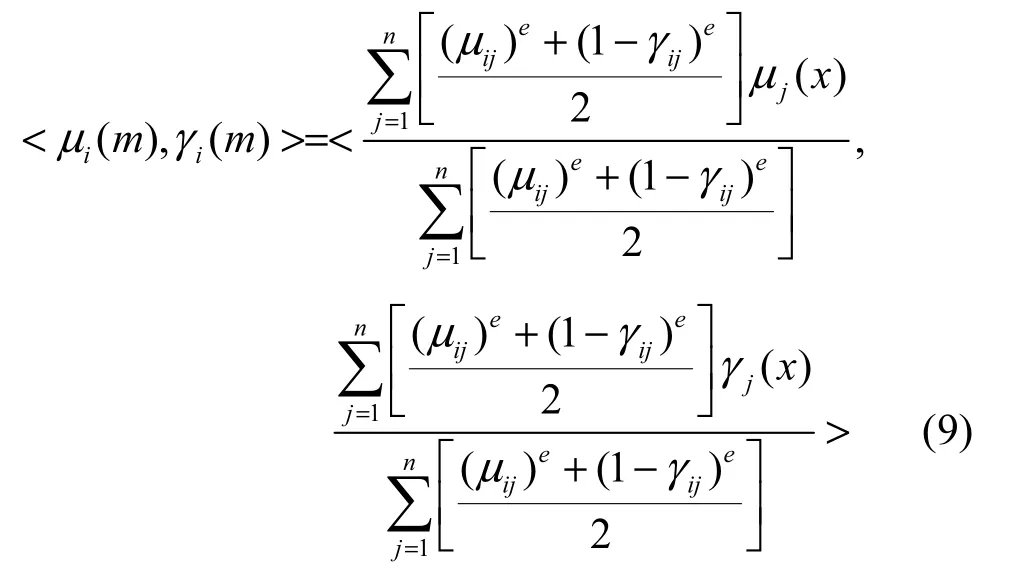
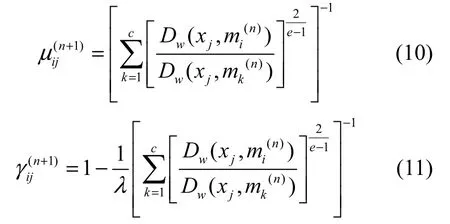
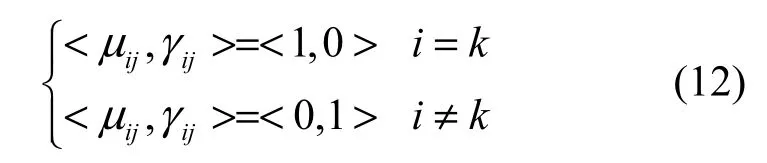
表1给出构建直觉模糊时间序列片段算法，通过直觉模糊C均值聚类，得到最优聚类中心，将聚类中心添加到时间序列片段，根据长期预测规模的需求，分别取不等长的时间序列片段作为训练数据。该算法将原始时间序列直觉模糊化为不等长序列片段，生产规则库并作为时间序列预测的依据。

算法1直觉模糊时间序列片段算法

输入：测试数据X，时间序列片段长度w，聚类数c,序列片段间隔d，最大迭代次数r

输出：直觉模糊时间序列片段库Base

Begin

在时刻τ沿 X滑动窗口 w,建立 X子序列,

根据式(6)直觉模糊化子序列 S；

for k=1 to r

根据式(10)、式(11)计算中心的隶属度和非隶属度函数

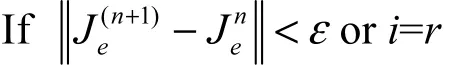
Break；

end

end

3.3 基于DTW的long-term IFTS预测模型

DTW 是一种距离测度与时间规划结合的非线性测量技术，通过弯曲矩阵可以有效测量非等长时间序列片段的曲线相似度，对于长期时间序列预测有很好的适用性。表2给出计算2个直觉模糊时间序列DTW距离的算法，对于2个直觉模糊数a和b，其隶属度和非隶属度函数分别为和那么定义直觉模糊数的距离d(a,b)由式(13)计算得到。

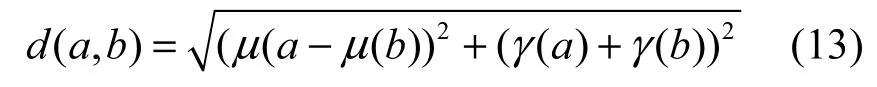
算法中min_cor函数表示之前路径对应的最小代价值的坐标。最后得到2个n×m的矩阵，分别称为代价矩阵cost和弯曲路径矩阵path。算法2通过计算2个直觉模糊时间序列的最小代价路径，作为这2个时间序列的DTW距离，在预测算法中调用该算法，得到的DTW距离作为长期直觉模糊序列规则库匹配的标准。

算法2直觉模糊DTW算法

输入：直觉模糊时间序列片段 A，B，序列长度n，m,DTW(A,B)

输出：n×m代价矩阵cost和弯曲路径矩阵path

Begin

设一个IFTS A=a1,a2,…,an,隶属度和非隶属函数分别为

设一个IFTS B=b1,b2,…,bn,隶属度和非隶属函数分别为

根据式(12)计算d(ai,bj)；//序列片段坐标距离

长期直觉模糊时间序列预测问题就是利用训练数据构建直觉模糊时间序列片段库，通过序列片段相似度匹配算法进行搜索，找出最相似的时间序列片段作为预测基础，最后计算得到预测输出结果。文献[13,16]利用欧式距离进行时间序列片段匹配，对于非等长时间序列片段，只截取了较短片段进行距离计算并得到预测结果，模型精度有限，本节提出一个基于直觉模糊DTW距离的预测算法，并通过实验证明其有效性。

算法3为基于DTW的long-term IFTS 预测算法。首先由算法1构建一个规模为n的直觉模糊时间序列片段库，分别计算每条片段到待测序列与Base中片段的DTW距离，取代价矩阵最小的片段作为匹配序列。接着计算前q−d项匹配序列与待测序列的DTW距离和预测距离e，最后将匹配向量后d项序列 match( ～ d)与预测距离e的和作为最终预测结果。当匹配序列方差将当前时间序列片段添加到原片段库Base，从而达到动态更新和维护序列片段库的目的。

算法3基于DTW的long-term IFTS预测算法

输入：直觉模糊时间序列片段库Base，规模为n，窗口长度l，预测长度d，历史数据p，τ时刻待测序列

输出：预测结果

Begin

for i=1 to n

从Base 中选择一个 IFTS Bq=b1,b2,…,bq;

DTW(Ap,Bq);

Wp,q=(w1,w2,…,wk…,wK);//最佳弯曲路径

Ifδ(A,B)=min(DTW(A,Base))

match=B;//匹配时间序列片段

else

Base−B;//删去时间序列片段

end

DTW(A,match(q−d));//计算待测序列与匹配序列前q−d项的DTW距离

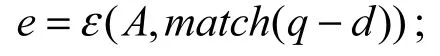
通过式(7)去直觉模糊化 Fτ′+1;

本节提出的基于DTW的long-term IFTS预测模型，由 3个算法构成，算法 1通过直觉模糊聚类方法，将原始时间序列直觉模糊化为不等长序列片段，生产规则库。算法 2计算 2个直觉模糊时间序列的DTW距离，在预测算法中调用该算法，作为长期直觉模糊序列规则库匹配标准。算法 3计算代价矩阵最小的片段作为匹配序列，最后求匹配向量后与预测距离之和得到预测结果。

4 实验与分析

4.1 合成数据预测

为了说明本文提出的基于 DTW 的 long-term IFTS预测模型的有效性，将该模型应用于文献[15,16]中的一个合成数据集，如图3所示。该数据集为一个包括60个数据点的时间序列，前40个点作为训练数据，其余的作为测试数据。根据本文提出的模型，预测步骤如下。

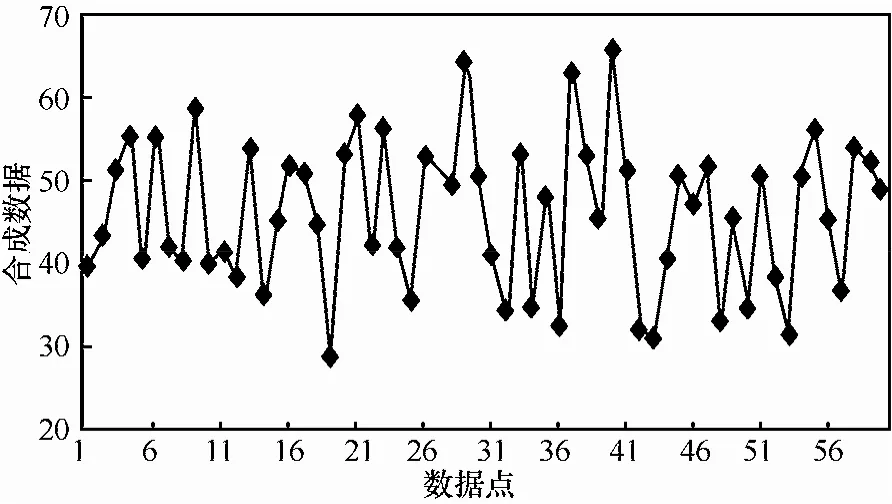
图3 长期预测合成数据

Step1为了同相关文献进行比较[13,16]，本文设定相同参数值，即时间序列片段长度 w=5,聚类数c=5，序列片段间隔d=1，沿时间序列数据X计算得到36个时间序列片段，前3项为

Step2定义全局论域 U=[20.0,70.0],设di=10,λ=0.95,U被划分为5个区间，即A1=[20,30],A2=[30,40],A3=[40,50],A4=[50,60],A5=[60,70]。根据式(6)直觉模糊化时间序列片段，设λ=0.95，前 3项直觉模糊化时间序列数据为：S1=(lt;0.38,0.61＞,lt;0.46,0.53＞,lt;0.63,0.37＞,lt;0.71,0.28＞,lt;0.41,0.58＞),S2=(lt;0.46,0.53＞,lt;0.63,0.37＞,lt;0.71,0.28＞,lt;0.41,0.58＞,lt;0.70,0.29＞),S3=(lt;0.63,0.37＞,lt;0.71,0.28＞,lt;0.41,0.58＞,lt;0.70,0.29＞,lt;0.44,0.55＞)。

Step3调用直觉模糊时间序列片段算法r=50，计算最优聚类中心，得到5个直觉模糊时间序列片段 m1、m2、m3、m4、m5，其隶属度和非隶属度函数如图4所示。将该时间序列片段添加至直觉模糊时间序列片段库Base。

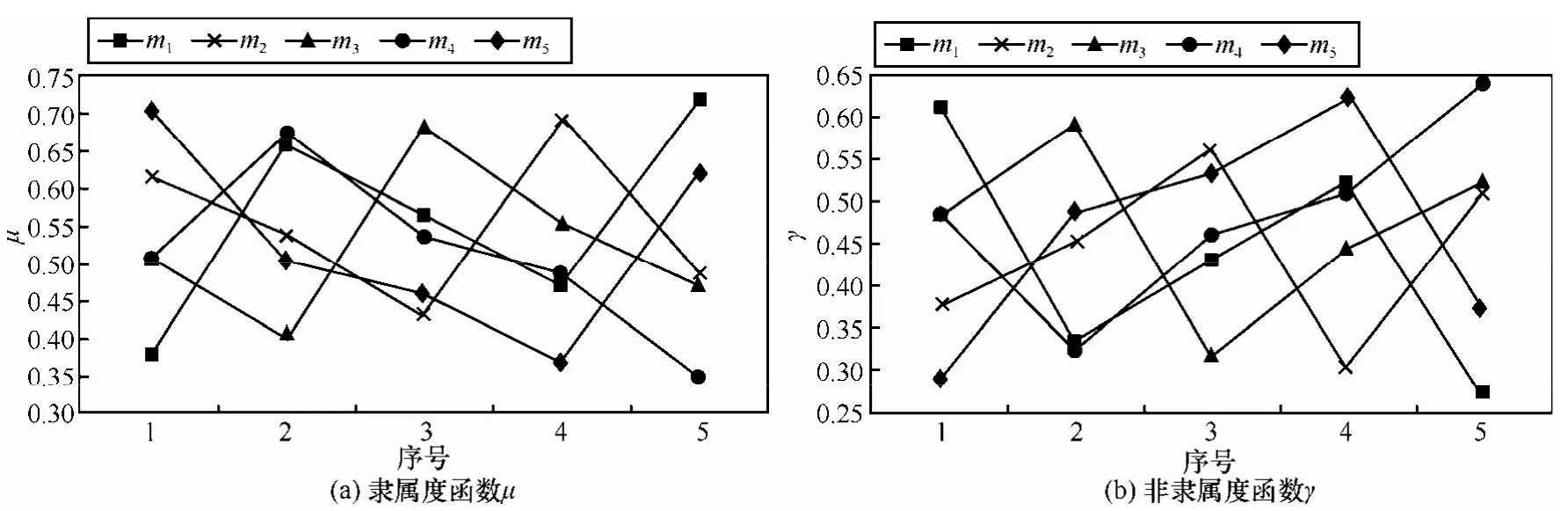
图4 直觉模糊时间序列片段

表1 直觉模糊时间序列片段库

Step4转至Step1，分别设训练数据窗口大小w=6，w=7，聚类数c=5，序列片段间隔d=1，调用直觉模糊时间序列片段算法，得到不等长时间序列片段并添加至Base，得到15条直觉模糊时间序列片段组成的Base库，如表1所示。

Step5设d=2，p=3，得到待测向量调用基于DTW的long-term IFTS预测算法。例如第 1条待测向量为(lt;0.63,0.36＞,lt;0.23,0.76＞,lt;0.21,0.78＞)，根据算法 3，分别计算待测向量A1与Base库中每条序列的直觉模糊DTW距离。得到与第13条序列片段最小DTW距离方差计算 DTW(A1,match(5))，得到距离期望ε=0.231，根据最后 2项序列值lt;0.66,0.33＞,lt;0.61,0.38＞ 计 算 得 到 预 测 结 果 为Fτ′+1=(＜0.43,0.56 gt;,＜0.38,0.61gt;)。

Step6根据式（7）对预测结果进行去直觉模糊化，得到精确值为(41.50,39.25)。其他预测结果如表2所示，分别将2项输出结果作为τ+1和τ+2时刻的预测值。

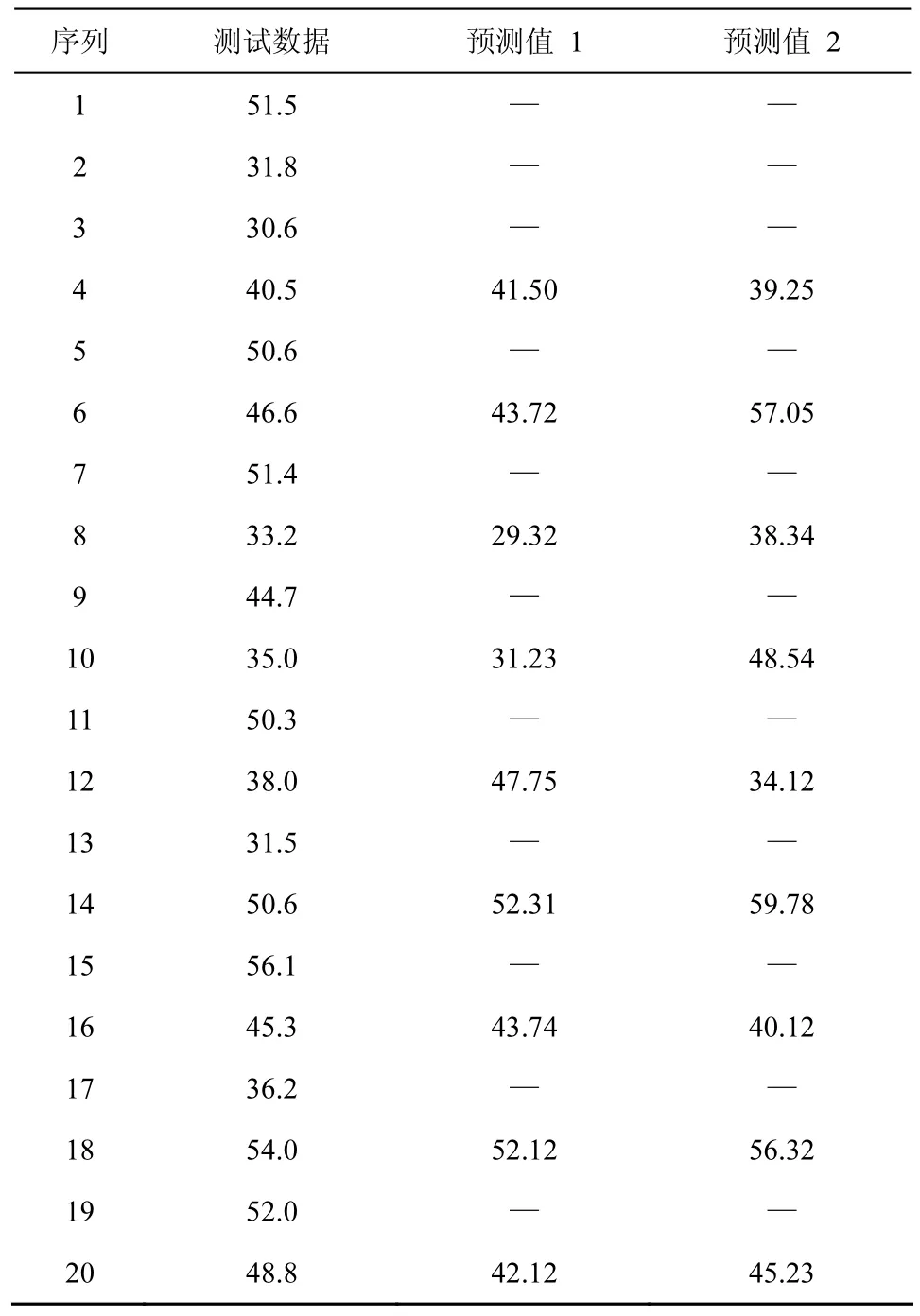
表2 合成数据长期预测结果

为了比较不同预测模型的精度，分别利用预测平均方差（MSE,mean square error）和平均预测误差率(AFER,average forecasting error rate)作为评价指标。

将本文提出的模型与文献[13,16]中的模型在该合成数据上进行比较，在本实验中，设置相同的时间序列窗口大小w和预测长度d，达到控制变量的目的，预测精确度随预测长度d的增加而降低，较短的预测长度可以得到较好的结果，聚类算法中聚类中心随聚类数c的增加而更加准确，但过多的聚类中心增加算法复杂度，同时增加系统规则库的规模。在预测问题中，过于精确的结果以牺牲系统开销为代价，通常在没有极大降低预测准确度的条件下减少聚类中心，该实验中实验数据为有限随机模式，实验对比结果如表3所示，本文提出的预测模型在MSE和AFER上均低于前2种模型，说明本文方法的参数选择合适，并且在长期时间序列预测中具有更高的精度。

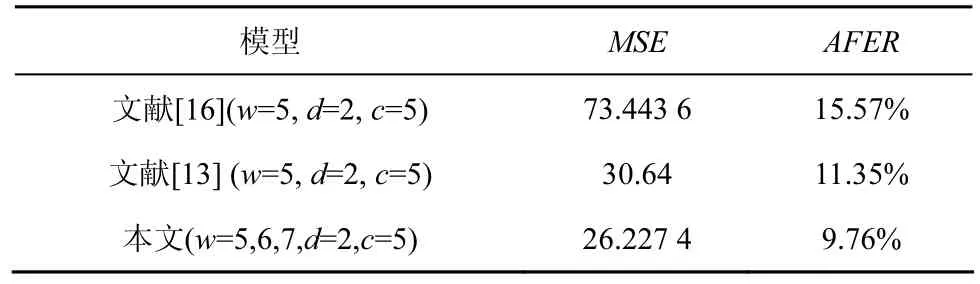
表3 MSE和AFER比较结果

4.2 气温数据预测

为了分析本文提出的长期直觉模糊时间序列模型在不同时间序列模式下的预测能力，将本文模型应用于另一温度数据集，北京市 2014年日平均气温(http∶//www.cma.gov.cn)，该数据集共包括 365个数据点。温度数据根据不同单位尺度包含不同时间序列变化趋势，例如随机模型（月）、季节模型（季）、长期趋势（半年）和周期模型（年），因此可以有效检验时间序列模型的泛化性能。

本文模型在不同时间单位上分别与文献[2,12,16,18]进行对比实验。考虑到相关模型只有单步输出结果，因此训练数据窗口长度分别设置为w=5、6、7，预测长度 d=1，预测窗口大小 w=6，聚类数设为c=7，前2个月共59个数据作为训练数据。由于文献[16]模型无法预测超出训练范围的数据，为了覆盖全年数据范围，将1月、4月、7月共92个数据作为训练数据。文献[2,12,18]中的模型将全局论域划分为8部分。重复实验10次取平均值，本文模型与文献[2,12,16,18]中模型对全年温度预测对比结果如图5和图6所示，2个月（3月、8月）气温预测对比结果如图7所示，MSE和AFER指标对比结果如表4所示。通过实验可以看出，在预测窗口大小参数选择上，最优预测结果为w=6，说明时间序列长度与预测没有线性相关性，通过多次训练可以得到较优值，本文提出的模型在全年范围和月范围上的时间序列预测结果均比相关文献精确，年级气温为周期性时间序列模式，月级为随机时间序列模式，本文模型仅8月份AFER指标比文献[18]略高，文献[2,12,18]在特定时间序列模式上进行全局论域划分可以得到较精确的结果，而将模型应用与几种时间序列模式的复合数据集上，预测结果不够理想，因此，说明本文模型比其他模型对于不同趋势的时间序列具有良好的适应性能。从实验参数设置可以看出，本文提出的模型不仅具有长期预测能力，相比文献[13,15,16]的长期时间序列预测模型，对训练数据集规模要求更小，能够有效处理预测范围超出训练数据的问题，动态维护直觉模糊时间序列库，从而减少系统复杂度。

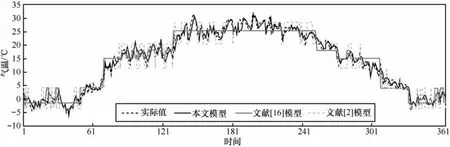
图5 本文模型与文献[2,16]模型对比结果

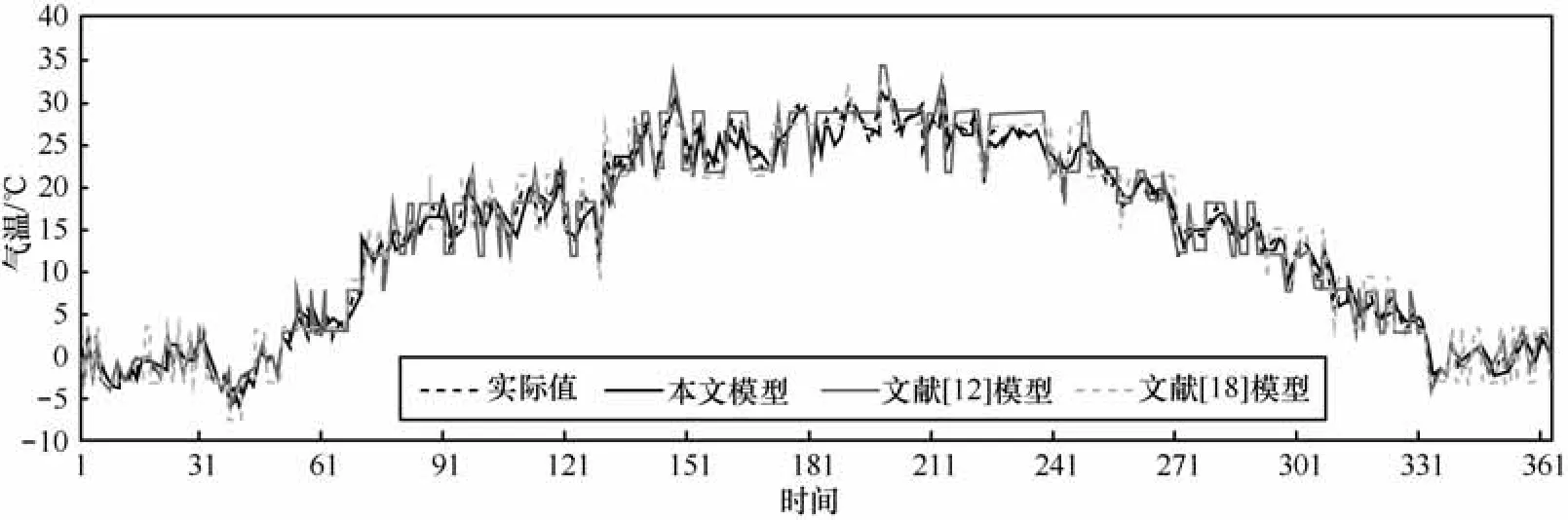
图6 本文模型与文献[12,18]模型对比结果

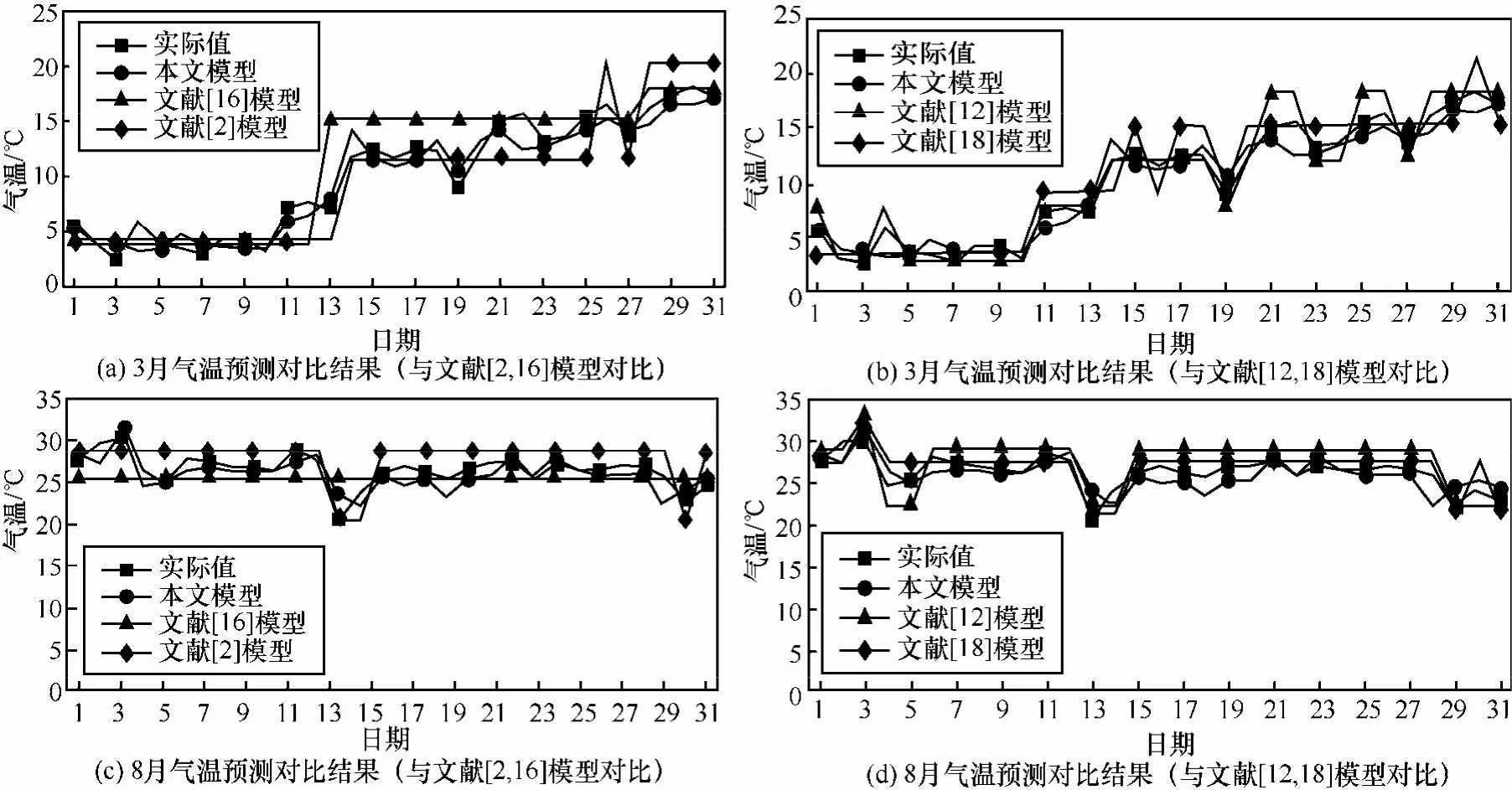
图7 2个月气温预测对比结果

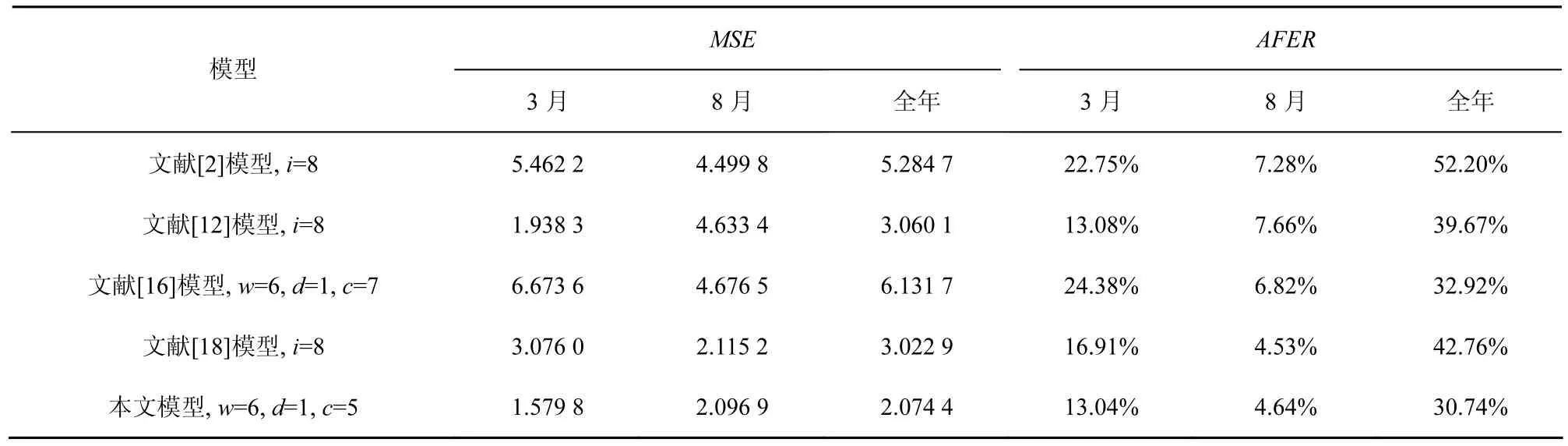
表4 气温预测MSE和AFER比较结果

5 结束语

本文针对现有直觉模糊时间序列模型训练数据复杂度高的问题，提出一种基于DTW的直觉模糊长期预测模型。通过直觉模糊C均值聚类构造非等长直觉模糊时间序列片段库，动态维护和更新数据库，有效解决现有文献中模型过度依赖训练数据库规模的现象，基于DTW距离的直觉模糊时间序列片段相似度计算方法，克服不等长时间序列片段匹配问题。该模型在预测数据超出训练数据范围的情况下，依然可以根据时间序列片段相似匹配度预测数据变化趋势，适用于不同模式的时间序列预测问题。通过实验，预测结果的MSE和AFER指标均表明该模型比现有文献更准确，是一种有效且泛化性能较好的长期预测模型。

[1]SONG Q,CHISSOM B S. Forecasting enrollments with fuzzy time series—part I[J]. Fuzzy Sets Systems,1993,54(1): 1-9.

[2]HUANG Y L,HORNG S J,HE M X,et al. A hybrid forecasting model for enrollments based on aggregated fuzzy time series and particle swarm optimization[J]. Expert Systems with Applications,2011,38(7):8014-8023.

[3]WANG L Z,LIU X D,PEDRYCZ W. Effective intervals determined by information granules to improve forecasting in fuzzy time series[J].Expert Systems with Applications,2013,40(14): 1465-1470.

[4]WEI L,CHEN X Y,PEDRYCZ W,et al. Using interval information granules to improve forecasting in fuzzy time series[J]. International Journal of Approximate Reasoning,2015,57(11): 1-18.

[5]CAI Q S,ZHANG D F,ZHANG W. A new fuzzy time series forecasting model combined with ant colony optimization and auto-regression[J].Knowledge-Based Systems,2015,74(11): 61-68.

[6]EGRIOGLU E,ALADAG C H,YOLCU U. Fuzzy time series forecasting with a novel hybrid approach combining fuzzy C-means and neural networks[J]. Expert Systems with Applications,2013,40(3):854-857.

[7]PARK J,LEE D J,SONG C K,et al. TAIFEX and KOSPI 200 forecasting based on two-factor high-order fuzzy time series and particle swarm optimization[J]. Expert Systems with Applications,2010,37(2):959-967.

[8]CHEN S M,CHEN S W. Fuzzy forecasting based on two-factors second-order fuzzy-trend logical relationship groups and the probabilities of trends of fuzzy logical relationships[J]. IEEE Transactions on cybernetics,2015,45(3): 405-416.

[9]ASKARI S,MONTAZERIN N. A high-order multi-variable fuzzy time series forecasting algorithm based on fuzzy clustering[J]. Expert Systems with Applications,2015,42(9): 2121-2135.

[10]CASTILLO O,ALANIS A,GARCIA M,et al. An intuitionistic fuzzy system for time series analysis in plant monitoring and diagnosis[J].Applied Soft Computing,2007,7(4): 1227-1233.

[11]郑寇全,雷英杰,王睿,等. 直觉模糊时间序列建模及应用[J]. 控制与决策,2013,28(10): 1525-1530.ZHENG K Q,LEI Y J,WANG R,et al. Modeling and application of IFTS[J]. Control and Decision,2013,28(10): 1525-1530.

[12]GANGWAR S S,KUMAR S. Probabilistic and intuitionistic fuzzy sets-based method for fuzzy time series forecasting[J]. Cybernetics and Systems.2014,45(4): 349-361.

[13]郑寇全,雷英杰,王睿,等. 参数自适应的长期 IFTS预测算法[J].系统工程与电子技术,2014,36(1): 100-104.ZHENG K Q,LEI Y J,WANG R,et al. Method of long-term IFTS forecasting based on parameter adaptation[J]. Systems Engineering and Electronics,2014,36(1): 100-104.

[14]郑寇全,雷英杰,王睿,等. 基于确定性转换的IFTS预测[J]. 应用科学学报,2013,31(2): 204-211.ZHENG K Q,LEI Y J,WANG R,et al. Prediction of IFTS based on deterministic transition[J]. Journal of Applied Sciences,2013,31(2):204-211.

[15]郑寇全,雷英杰,王睿,等. 基于矢量量化的长期直觉模糊时间序列预测[J]. 吉林大学学报(工学版),2014,44(3): 795-800.ZHENG K Q,LEI Y J,WANG R,et al. Long-term intuitionistic fuzzy time series forecasting based on vector quantization[J]. Journal of Jilin University (Engineering and Technology Edition),2014,44(3):795-800.

[16]LI S T,KUO S C,CHEN Y C,et al. Deterministic vector long-term forecasting for fuzzy time series[J]. Fuzzy Sets and Systems,2010,161(13): 1852-1870.

[17]HUNG K C,LIN K P. Long-term business cycle forecasting through a potential intuitionistic fuzzy least-squares support vector regression approach[J]. Information Sciences,2013,224(Complete): 37-48.

[18]LEE H S,CHOU M T. Fuzzy forecasting based on fuzzy time series[J]. International Journal of Computer Mathematics,2004,81(7): 781-789.

Long-term intuitionistic fuzzy time series forecasting model based on DTW

FAN Xiao-shi,LEI Ying-jie,LU Yan-li,WANG Ya-nan

(Air and Missile Defense College,Air Force Engineering University,Xi’an 710051,China)

In existing fuzzy time series forecasting models,the intuitionistic fuzzy relationship groups and deterministic transition rules excessively relied on scale of the training data. A long-term intuitionistic fuzzy time series (IFTS)forecasting model based on DTW was proposed. The IFTS segment base was constructed by IFCM. The complexity of system was reduced by dynamic update and maintaining of the rule base. The computing method of IFTS segments similarity based on the distance of DTW was proposed,which was valid for matching unequal length time series segments. The proposed model implements on the synthetic and the temperature dataset,which including different time series patterns,respectively. The experiments illustrate that the forecasting accuracy of the proposed model is higher than the others on the different tendency patterns of time series. The proposed model overcomes the limitation of single time series pattern and improves the generalization ability.

DTW,intuitionistic fuzzy sets,IFCM clustering,time series,forecasting

The National Natural Science Foundation of China (No.61309022)

TP393.08

A

2016-01-13；

2016-05-03

国家自然科学青年基金资助项目（No.61309022）

10.11959/j.issn.1000-436x.2016160

范晓诗（1988-），男，陕西西安人，空军工程大学博士生，主要研究方向为网络信息安全。

雷英杰（1956-），男，陕西渭南人，博士，空军工程大学教授、博士生导师，主要研究方向为网络信息安全、智能信息处理。

路艳丽（1980-），女，陕西渭南人，博士，空军工程大学讲师，主要研究方向为智能信息处理。

王亚男（1988-），女，山东青岛人，空军工程大学博士生，主要研究方向为网络信息安全。