同时同频全双工宽带射频自干扰抵消性能分析

王俊，赵宏志，马万治，唐友喜，卿朝进

(1. 电子科技大学通信抗干扰技术国家级重点实验室，四川 成都 611731；2. 西华大学电气信息学院，四川 成都 610039)

同时同频全双工宽带射频自干扰抵消性能分析

王俊1，赵宏志1，马万治1，唐友喜1，卿朝进2

(1. 电子科技大学通信抗干扰技术国家级重点实验室，四川 成都 611731；2. 西华大学电气信息学院，四川 成都 610039)

针对同时同频全双工场景中，宽带射频自干扰抵消方案缺乏性能分析这一问题，以多抽头射频域自干扰抵消结构为基础，以最小化剩余自干扰信号功率为准则，讨论了该结构中各抽头参数的最优解，进而分析了可实现的最佳自干扰抑制效果。数值与仿真结果表明，多抽头射频域自干扰抵消结构最佳的自干扰抑制性能与自干扰信号带宽、载波频率以及抽头时延与自干扰信道多径时延之差有关。信号带宽越大，或抽头时延与自干扰信道多径时延之差越大，干扰抑制性能越差；干扰抑制效果随载波频率的增加近似呈周期性振荡。

无线通信；同时同频全双工；射频自干扰抵消；宽带；多抽头

1 引言

目前，全球第五代移动通信（5G）技术研究已经如火如荼地展开，其中的一个主要技术目标是提高频谱的利用率[1]。与传统的时分双工、频分双工相比，同时同频全双工（CCFD, co-time and co-frequency full duplex）技术有着更高的频谱利用率[2,3]，因此它成为了5G技术的重要候选方案。然而，由于在同一频段上同时传输上下行数据，同时同频全双工接收机会受到本地发射机的大功率干扰[4,5]。考虑到模数转换器（ADC, analog to digital converter）的动态范围有限[5]，在ADC量化之前，同时同频全双工接收机有必要首先在射频域对接收信号进行自干扰抑制。

同时同频全双工系统中射频域自干扰信号抵消的主要思想是对射频自干扰信号进行估计并将其从接收射频信号中去除，早期的研究主要考虑窄带自干扰信号场景[6～9]。其中，文献[6]利用本地发送射频信号作为重建自干扰的参考信号，通过调整参考信号的相位、幅度和时延实现自干扰信号的恢复；文献[7,8]在射频域采用由正交、同相2条支路构成的自干扰信号估计结构，通过调整2条支路的衰减器增益，实现自干扰信号的估计；文献[9]则在基带估计出自干扰信号，经过一个额外的射频通道后生成射频自干扰估计信号。上述文献阐述的方法只适用于窄带自干扰信号场景，并且仅通过实验验证了射频域自干扰抵消方案的可行性，缺乏相应的理论分析。

鉴于现实工程应用的场景多为宽带场景，文献[10～17]研究了同时同频全双工系统中宽带自干扰信号的射频抵消方法。其中，文献[10,11]针对正交频分复用（OFDM, orthogonal frequency division multiplexing）宽带全双工系统，提出了一种基带辅助的单抽头自干扰抑制方法。具体地，在基带分别估计各个子载波的自干扰信号，经过快速傅里叶逆变换（IFFT, inverse fast Fourier transform）、数模转换以及上变频之后，在射频域生成一路时域自干扰估计信号并将其抵消掉。由于这种结构没有以发射射频输出作为自干扰估计的参考信号，它不能抵消发射射频通道产生的非线性自干扰。因此文献[12～17]针对一般的宽带全双工系统，提出了多抽头的射频域自干扰抵消结构，其基本思想是以发射端射频输出作为参考信号，通过多抽头的结构来模拟宽带自干扰信道的多径效果，每个抽头包含独立的可调衰减器和可调移相器，从而恢复出接收到的宽带自干扰信号。为了不改变全双工设备的电路结构，现有多抽头自干扰抵消方法多采用自适应搜索的方式对可调衰减器和移相器的值进行搜索，包括差分最速下降（DSD, differential steepest descent）[13]、最小均方误差（LMS, least mean squares）[14,15]以及扰动线性搜索（DLS, dithered linear search）[16,17]等自适应搜索方法。

目前，虽然针对宽带同时同频全双工场景下的射频域自干扰抵消技术研究已有很多，但上述文献均着重于阐述自干扰抵消方法和实验验证方案与结果，未对宽带自干扰抑制性能进行理论评估。因此，本文考虑自干扰信号为宽带信号的同时同频全双工场景，以最小化剩余自干扰信号功率为准则，对多抽头射频域自干扰抵消结构的自干扰抑制性能进行了理论分析。分析了该结构中各抽头参数的最优解以及干扰抵消后的剩余干扰信号功率，进而给出了该结构能够达到的最佳自干扰抵消效果，即实现了对多抽头结构能够实现的最大自干扰抑制性能的评估。特别地，以双抽头干扰抵消结构为例，本文进一步给出了其权向量最优解和自干扰抑制能力的简化表达式，并分析了双抽头干扰抵消结构的最优性能与各系统参数之间的关系。最后结合仿真分析了抽头时延与自干扰信道多径时延之差、干扰信号带宽以及载波频率因素对宽带自干扰抵消效果的影响。本文的研究结果可以为工程实现中宽带同时同频全双工系统射频域自干扰抵消方案的设计、实验验证以及性能评估提供参考。

2 系统模型

本文采用的同时同频全双工系统模型如图1所示[7]。其中，下标l表示近端发射信号参数，下标f表示远端发射信号参数。

近端发射机中的本地发送比特流bl(k)经过调制、脉冲成形、数模转换(DA, digital to analog conversion)以及射频前端处理馈入发射天线。近端接收机不仅接收到来自远端的期望信号，同时还接收到本地发射的自干扰信号xl(t)。在近端接收机中，首先对接收射频信号r(t)进行多抽头的自干扰抵消；经模数转换（AD, analog to digital conversion）、匹配滤波后，解调得到远端期望信号的估计值

2.1 发射机模型

图1 同时同频全双工系统模型

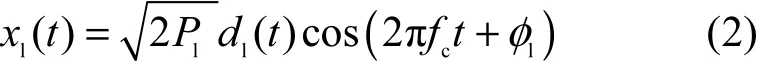
其中，Pl是近端发射信号功率，φl为近端发射信号的载波初始相位。

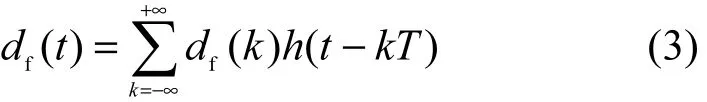
则远端发射机的射频信号输出xf(t)可表示为

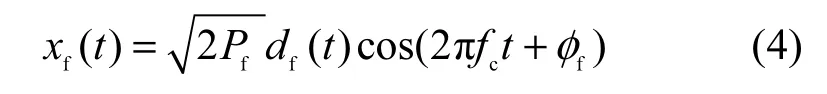
其中，Pf为远端发射信号功率，φf为远端发射信号的载波初始相位。

2.2 信道模型

根据图1所示的系统模型可知，在同时同频全双工收发信机中，接收射频信号可以写为

其中，rf(t)为远端期望信号，rl(t)为本地自干扰信号，n(t)表示接收信号中叠加的加性白高斯噪声。

在复杂的传播环境下，自干扰信号的传播路径不仅包括本地收发天线之间的直射路径，还包括许多反射和散射路径。因此，本文假设本地发射的信号经过M条无线传播路径到达接收机，则式(5)中的本地自干扰信号分量为[18]

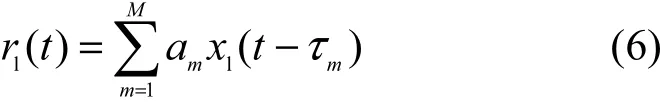
其中，M表示自干扰信道的多径数目，am为自干扰信道中第m条路径的幅度衰减，τm为第m条路径的传输时延。

2.3 接收机模型

近端接收机首先对接收信号进行射频域的多抽头自干扰抵消。干扰抵消后的信号经过下变频、模数转换、匹配滤波后，解调得到远端发送比特流的估计值。在上述过程中，射频域的自干扰抵消是正确解调远端期望信号的前提。射频域自干扰抵消后的剩余干扰信号z(t)可以写为

在窄带自干扰信号场景中，与发射信号的基带符号周期T相比，式(6)中的自干扰信道最大传输时延τm很小，即τm?T，使基带成形脉冲满足

则近端接收机接收到的多径自干扰信号可以近似为单径信号。通过对单径自干扰信号的幅度衰减、相移的估计，即可实现窄带自干扰信号的估计和抑制[7,8]。在宽带的自干扰场景中，式(8)近似不成立，即无法通过对等效单径自干扰信号的估计实现自干扰信号的恢复。因此，针对宽带自干扰场景，本文考虑多抽头的射频域自干扰抵消结构[12]，如图2所示。其中，N表示多抽头自干扰抵消结构的抽头数量，为第n (1≤n≤N)个抽头的增益，为第n个抽头的相位偏移，为第n个抽头的时延。为不失一般性，假设各抽头时延之间两两不相等。

图2 多抽头的射频域自干扰抵消结构

3 多抽头干扰抵消性能分析

实际工程中，射频信号的延时采用延迟线来实现，一旦延迟线的参数确定后，其能实现的信号时延便固定下来。因此，本节考虑各抽头时延固定的情况，以干扰抵消后的剩余自干扰功率最小化为目标，分析各抽头中相位偏移、抽头增益的最优取值，并探讨多抽头结构能够实现的自干扰抵消性能。

3.1 最优权矢量

依据傅里叶变换规则，2.2节中自干扰信道的频率响应Hc(f)为[19]

类似地，图2中多抽头自干扰估计结构的频率响应Hs(f)为[19]

进一步，将式(10)中的结果重写为向量乘积的形式

其中，上标“T”、“*”分别代表矩阵的转置和共轭操作，且权矢量W、频点f的相位旋转因子矢量分别定义为

根据2.3节中的多抽头自干扰抵消结构，得到干扰抵消后的等效剩余自干扰信道频响Hr(f)

则干扰抵消后的剩余自干扰信号功率谱密度Sr(f)为[20]

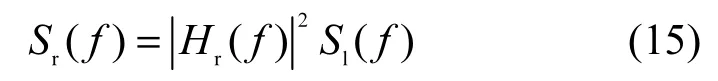
其中，Sl(f)表示本地发送射频信号xl(f)的功率谱密度。

假设近端发射机采用sinc函数作为发射信号的成形脉冲函数，则本地发送射频信号的功率谱密度在信号带宽B内是平坦的，且信号带宽为基带符号速率的倒数[21]

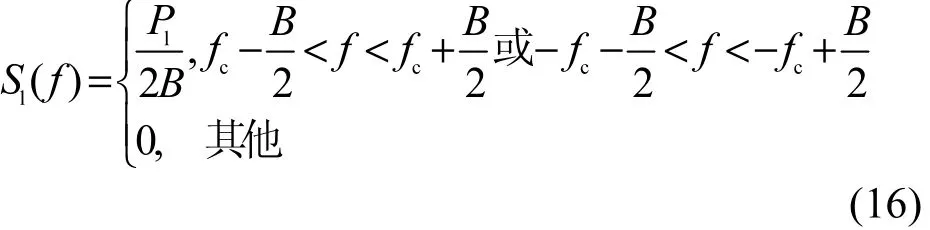
结合式(15)、式(16)，剩余自干扰信号的总功率Pr为

将式(17)中的右边部分展开，剩余自干扰信号的功率可以写为

其中，上标“H”表示矩阵的共轭转置。

根据式(18)可以看出， Pr是W的二次函数，即Pr是以W为自变量的多维碗状曲面。由于W是复向量，根据文献[20]中定义的复向量梯度算子，可以得到剩余干扰功率 Pr的复值梯度向量∇Pr。∇Pr的第k个元素为

当复值梯度向量的实部、虚部均为0时，剩余干扰功率 Pr取得极值[20]。按照式(19)给出的复值梯度向量，对剩余干扰功率 Pr求梯度得到

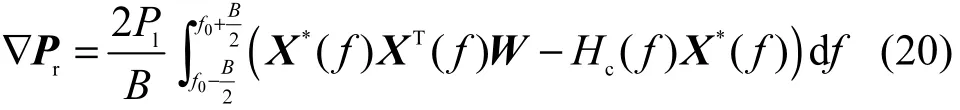
为了方便后续的分析，将式(20)重写为

其中矩阵R、向量Q分别定义为

结合式(9)、式(13)，化简矩阵R、向量Q。

其中，qn为向量Q中的第n个元素，rij为矩阵R中第i行第j列元素，sinc(⋅)函数的定义为

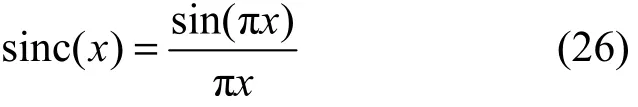
将式(21)中的复值梯度向量置为零并求解得到：当R可逆时，W有且只有一个解使复值梯度向量∇Pr为全0向量，即剩余干扰信号功率曲面只存在一个极值点；当R不可逆时，W有多个解使复值梯度向量∇Pr为全0向量，即剩余干扰信号功率曲面存在多个极值点，此时该曲面的性能不易评估。由式(25)可知，R中的元素只与各抽头的固定时延、干扰信号带宽以及载波频率有关。当上述 3种参数给定时，矩阵R便可根据式(25)计算出来。矩阵R确定之后，本文通过计算其行列式验证矩阵R是否可逆[22]。具体地，若R的行列式值等于0，则矩阵R不可逆；反之则可逆。本文考虑矩阵R可逆的情况，当W满足式(27)时， Pr取得极值。同时，3.2节将会证明此时 Pr取得极小值，即干扰抵消后的剩余干扰功率最小。

根据式(27)可知，多抽头干扰抵消结构的最优权矢量与矩阵Q、R的具体取值有关。结合式(24)、式(25)，最优权矢量的取值与信号带宽、载波频率以及抽头时延与自干扰信道多径时延两两之差有关。结合式(12)，在计算出最优的权矢量Wopt后，可得最小化剩余干扰功率准则下，最优的抽头增益以及相位偏移。

3.2 剩余干扰功率

结合式(22)、式(23)，将式(18)中的剩余自干扰信号功率化简为

其中，

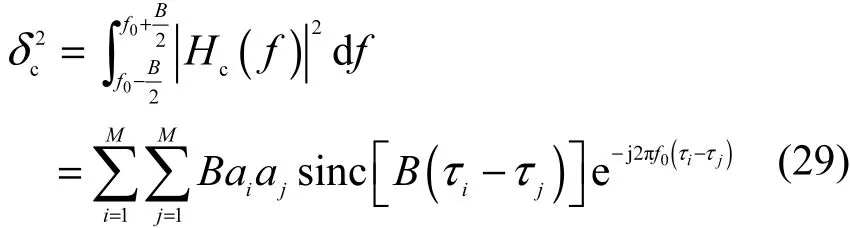
将式(27)中的最优权矢量Wopt代入到式(28)中，化简得到干扰抵消后的最小剩余干扰功率Pr-opt。

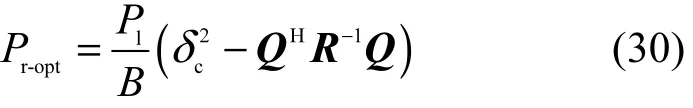
重新整理式(28)，则任意权矢量W下的剩余干扰功率Pr为

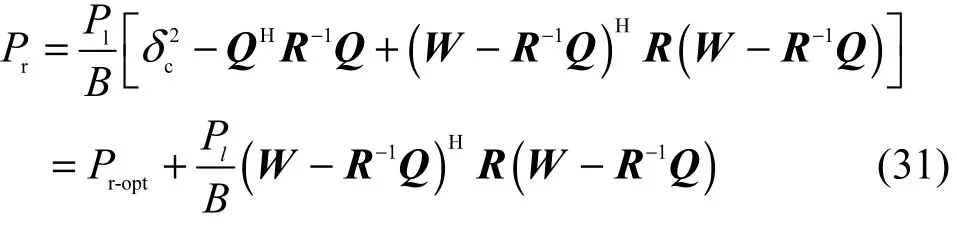
根据R的定义可知，R为半正定矩阵，式(31)中剩余干扰功率 Pr在W=R−1Q时取得最小值，且最小值在式(30)中给出。因此，Pr-opt为同时同频全双工系统中射频域多抽头自干扰抵消后的最小剩余干扰功率。进一步，定义干扰抑制比表示干扰抵消前后的自干扰信号功率之比，则多抽头干扰抵消结构的最大干扰抑制比ISR表示为

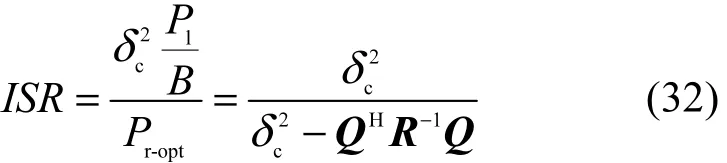
根据式(32)可知，多抽头干扰抵消结构的最佳干扰抵消性能与矩阵Q、R的具体取值有关。结合式(24)、式(25)，该性能与信号带宽、载波频率以及抽头时延与自干扰信道多径时延两两之差有关。从式(27)、式(32)中可以看出，对矩阵R求逆是深入分析多抽头干扰抵消结构最优权矢量取值和最佳自干扰抵消性能的关键。但是由式(25)中R的定义可知，R并非可以分析出其逆矩阵一般形式的特殊矩阵，则多抽头干扰抵消结构最优权矢量、最佳自干扰抵消性能的一般形式很难深入分析。因此，只能对特定的R进行数值计算，从而观察其干扰抵消效果以及各参数对性能的影响。接下来本文考虑一种简化的场景，以单径自干扰信号为例，采用双抽头干扰抵消结构，给出最优权矢量的解析表达并进一步分析其自干扰抑制性能。

4 双抽头干扰抵消性能分析

本节以双抽头干扰抵消结构为例，考虑单径的自干扰信道场景，化简并分析其最优权矢量以及自干扰抑制性能。根据式(9)，可以写出单径自干扰信道的频率响应

其中，a、τ分别代表自干扰信道的幅度衰减和传输时延。

根据式(10)，双抽头干扰抵消结构的频率响应为

结合式(24)、式(25)和式(29)，双抽头干扰抵消模型中的参量Q、R以及分别化简为

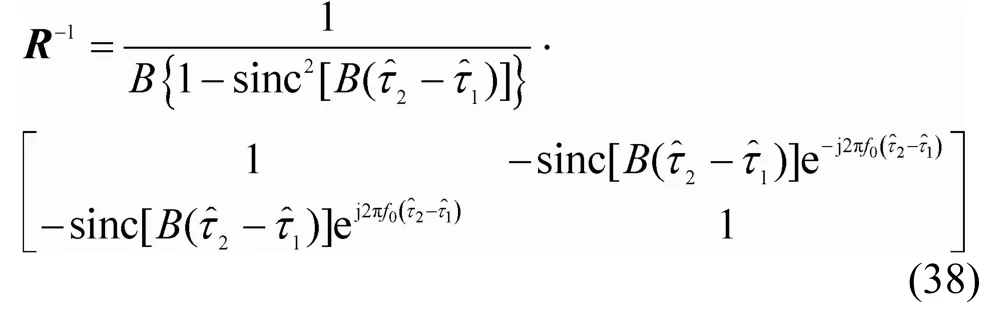
结合式(27)，双抽头干扰抵消结构的最优权矢量为

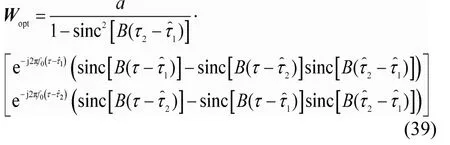
结合式(30)，干扰抵消后的最小剩余自干扰功率化简为

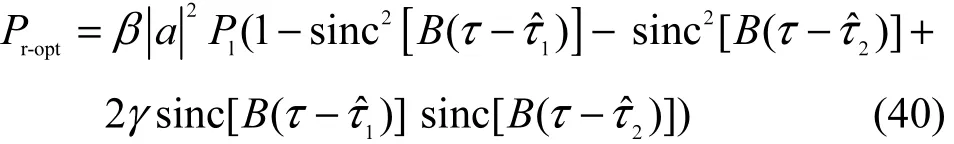
其中，参数γ、β分别定义为

因此，考虑单径的自干扰信道场景，双抽头干扰抵消结构的最大干扰抑制比为

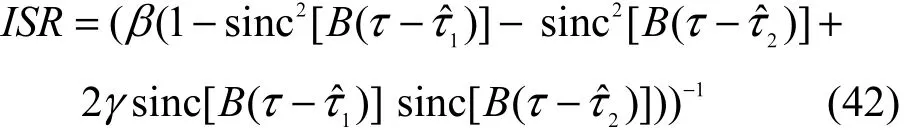
从式(39)、式(42)可以看出，针对单径自干扰信号的双抽头干扰抵消结构，其最优权矢量由自干扰信号带宽、载波频率以及抽头时延与自干扰传输时延之差决定；其最佳的自干扰抑制效果与自干扰信号带宽、抽头时延与干扰传输时延之差有关。自干扰信号带宽越宽，需要拟合的自干扰信道频点越多，双抽头结构拟合出的自干扰信道误差变大，干扰抑制效果变差；抽头时延与干扰传输时延之间差距越小，拟合出的信道频响越接近真实的自干扰信道频响，干扰抑制效果越好。

5 数值与仿真结果

考虑同时同频全双工通信场景，针对以最小化剩余干扰功率为准则的射频域多抽头干扰抵消结构，利用Matlab仿真软件进行性能仿真和验证。

5.1 多抽头干扰抵消结构

考虑室内的同时同频全双工系统，其自干扰信道可视作收发天线位于室内的典型无线多径信道。鉴于 S-V（saleh-valenzuela）信道模型是室内多径信道建模应用最普遍的统计模型[23]，本节采用IEEE802.15.3a工作组推荐的基于修正S-V信道模型的CM1统计模型，该模型有效地建模了0～4 m通信距离下的视距（LOS，line of sight）超宽带室内信道[24]。具体地，根据 CM1模型中的统计参数随机生成一个信道实例，作为仿真的多径信道参数，由此得到的信道仿真参数如表1所示。值得注意的是，幅度衰减中的负号代表无线信号在传播过程中由反射引起的180°相位翻转。

本节的信号带宽设置为100 MHz。根据表1可知，自干扰信号传输的最大时延为26.2 ns，则自干扰信道的相干带宽近似为38 MHz[25]。因此，对于带宽为100 MHz的自干扰信号来说，自干扰信道是一个频率选择性衰落信道，此时，接收到的自干扰信号由多条可分辨路径的信号叠加组成，需要采用多抽头干扰抵消结构来进行抵消。

表1 信道仿真参数

文献[26]指出均衡器的阶数需要在最小均方误差性能与复杂度之间折中选取。由于多抽头干扰抵消结构中抽头数目的物理意义与均衡器的阶数类似，结合表1所示的信道仿真参数，本小节将多抽头干扰抵消结构的抽头数设置为 8，各抽头时延在0～28 ns之间等间隔设置，以实现多抽头干扰抵消结构的性能仿真与验证。当信号带宽为100 MHz、载波频率为2.4 GHz时，经计算，其对应的矩阵R行列式不为 0，即矩阵R可逆。因此，可按照式(27)计算出多抽头自干扰抵消结构的最优权矢量，如表2所示。

表2 多抽头自干扰抵消结构的最优权矢量

在表1所示的自干扰信道参数和表2所示的多抽头干扰抵消结构下，图3给出了干扰抵消前后，载波频率附近频点的自干扰信道频率响应，其中，f0=2.4 GHz，B=100 MHz。从图3可以看出，当载波频率为2.4 GHz时，在自干扰信号所处的2.35～2.45 GHz频带内，多抽头干扰抵消后自干扰信道频响幅度值下降了约40 dB，即在上述参数下，该结构能够实现的最佳自干扰抑制能力约为 80 dB(根据帕斯瓦尔定理，自干扰信号抑制效果等于干扰抑制前后等效自干扰信道频响幅度下降值的平方)。此外，从图中也可以看出，干扰抵消后的自干扰信道频响的幅度随频率振荡，从式(9)、式(10)中可以看出，这是因为抵消后的自干扰信道频响是有限个关于载波频率的复指数函数的线性叠加，由于复指数函数是周期振荡的函数，其线性组合后的函数也会随着自变量振荡。

图3 干扰抵消前后，等效自干扰信道频响的幅度响应

同样以表1所示的参数作为信道仿真参数，假设理想的信道测量，分别计算不同干扰信号带宽以及载波频率时的最优抽头权矢量（经计算，本节涉及的不同干扰信号带宽以及载波频率，其对应矩阵R的行列式均不为0，即矩阵R可逆，此时，多抽头干扰抵消结构的最优权矢量可被计算出来）。图4给出了载波频率为2.4 GHz时，不同信号带宽下多抽头干扰抵消结构的最佳干扰抑制性能，图5给出了干扰信号带宽为100 MHz时，不同载波频率下经多抽头干扰抵消后的剩余自干扰功率。

从图4可以看出，在上述仿真条件下，干扰信号带宽越大，干扰抑制的性能越差。这是因为信号带宽越宽，需要拟合的自干扰信道频带越宽，多抽头结构拟合出的自干扰信道误差越大，干扰抑制的性能越差。从图5可以看出，在上述仿真条件下，干扰抑制效果随载波频率的改变呈周期性振荡，这是因为在式(30)右边的各项中，载波频率均出现在复指数函数的指数部分。由于复指数函数是周期函数，当所有复指数函数存在一个公共周期时，最小剩余干扰功率会呈现出严格周期振荡的特点。

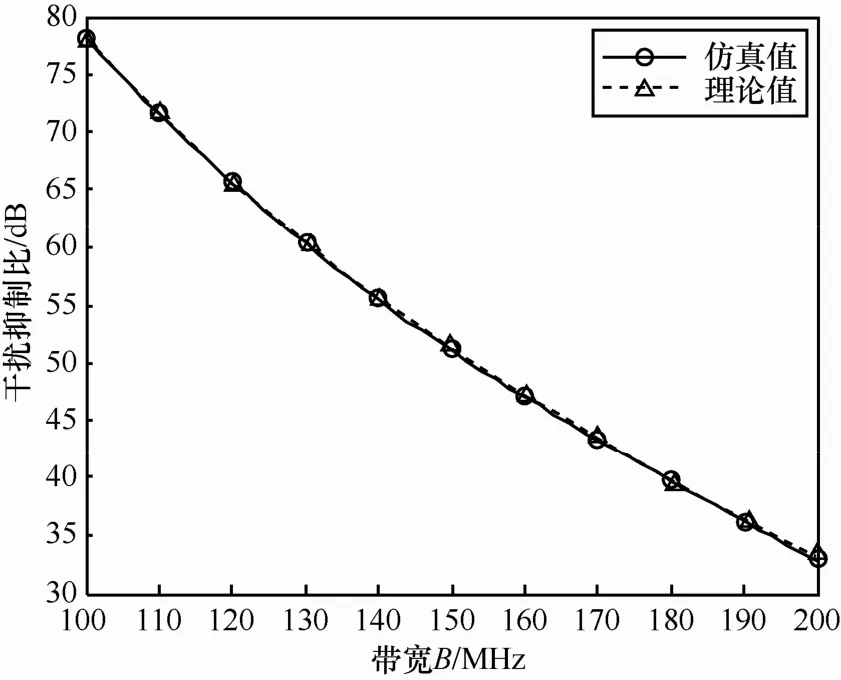
图4 不同信号带宽下，多抽头干扰抵消结构的干扰抑制性能

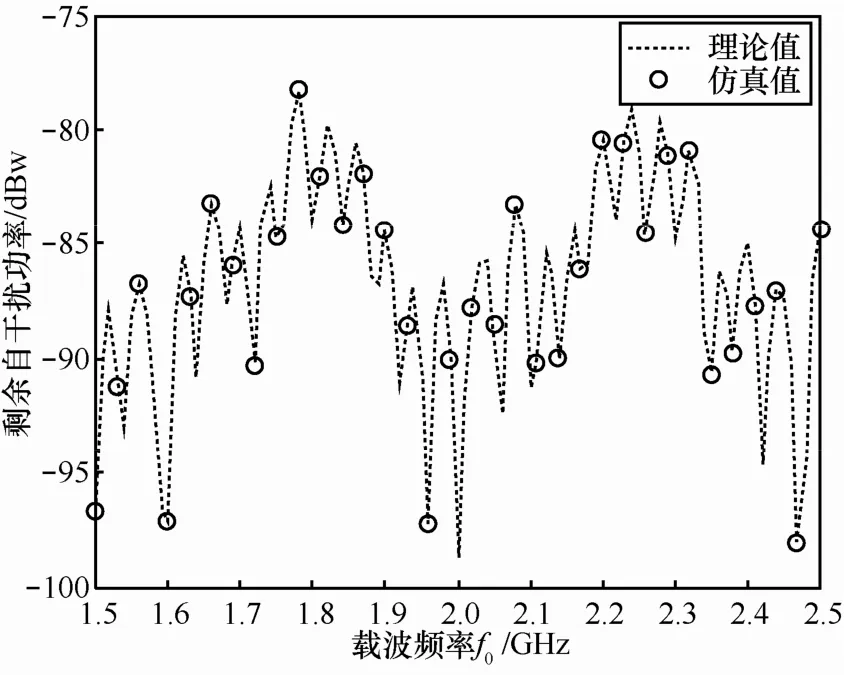
图5 不同载波频率下，多抽头干扰抵消后的剩余自干扰功率

5.2 双抽头干扰抵消结构

本节考虑单径自干扰信号，对双抽头干扰抵消结构的最佳干扰抑制性能进行仿真验证。图6给出了载波频率为2.4 GHz，干扰信号带宽为20 MHz，干扰传输时延为5.5 ns时，不同抽头时延设置对干扰抑制性能的影响。从图中可以看出，当固定抽头时延时，抽头时延距离干扰传输时延τ越小，干扰抑制性能越好。由式(42)可知，的位置可以互换，同时结合图6中的数值与仿真结果，当固定时，抽头时延越接近干扰传输时延τ，干扰抑制性能越好。产生上述现象的原因是当抽头时延与自干扰信道传输时延之间的差距越小时，双抽头结构拟合出的信道频响与真实自干扰信道频响之间误差越小，抵消后的干扰信道频响幅度就越小，剩余干扰信号功率越小。

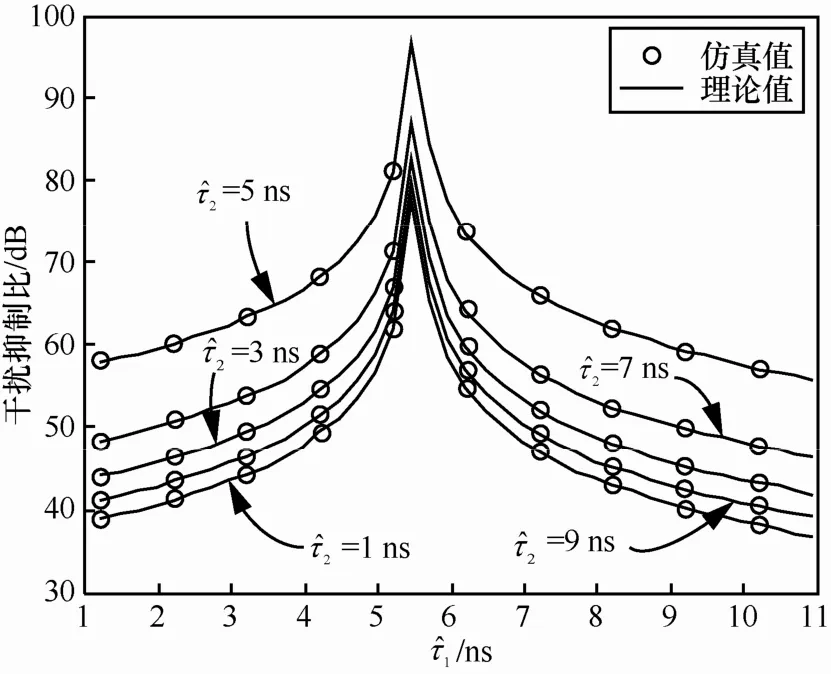
图6 不同抽头时延下，双抽头干扰抵消结构的自干扰抑制性能

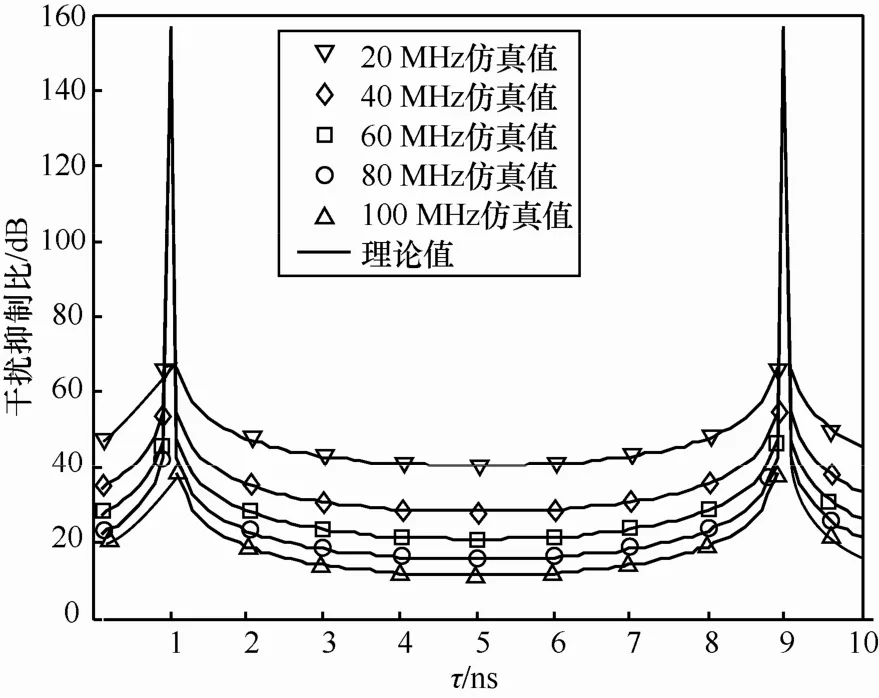
图7 不同干扰信号带宽下，双抽头干扰抵消性能随干扰传输时延的变化

图8 不同干扰传输时延下，双抽头干扰抵消性能随干扰信号带宽的变化

此外，本节还仿真对比了本文分析的自干扰抑制性能上界与已有多抽头自干扰抑制算法的性能。考虑到现有的多抽头自干扰抑制方法多采用自适应搜索对可调衰减器和可调移相器的值进行调整，具体包括DSD算法、LMS算法以及DLS自适应搜索方法。其中，LMS算法需要对各抽头信号单独进行下变频，大大增加接收机设计的复杂度和成本；而DSD算法是DLS算法的一种特例[17]，因此，将本文分析出的性能上界与 DLS自适应搜索算法的仿真结果进行比较。

设置干扰传输时延为25 ns，抽头1的传输时延为24 ns，抽头2的传输时延为74 ns，载波频率设置为2 GHz，信号带宽为10 MHz，信噪比为0 dB，干信比为60 dB。根据本文分析结果计算出的自干扰抑制比性能上界为42.6 dB。图9给出了随着迭代次数的增加，基于可变步长DLS搜索的自适应干扰抑制方法的干扰抑制性能的变化。

图9 随着迭代次数的增加，可变步长DLS自适应干扰抵消方法的干扰抑制性能

从图中可以看出，与本文分析的性能上界相比，DLS自适应干扰抑制算法的稳态性能存在着5 dB的性能损失。考虑到DLS搜索算法本质上是一个梯度下降算法，梯度下降算法的关键在于对梯度进行估计，若能实现理想的梯度估计，则其稳态干扰抑制性能即为自干扰抑制的性能上界；若梯度估计存在误差，则稳态干扰抑制性能会存在性能损失[20]。因此，由于DLS搜索算法中的随机梯度估计存在误差，与多抽头自干扰抑制结构的性能上界相比，DLS自适应干扰抑制会产生性能损失。

综上所述，在宽带场景下的同时同频全双工系统中，以最小化剩余干扰功率为准则时，多抽头干扰抵消结构的最佳干扰抑制性能与载波频率、干扰信号带宽以及抽头时延与干扰信道多径时延之差有关。数值与仿真结果显示，应用5.1节的仿真条件时，干扰信号带宽越大，多抽头干扰抑制性能越差，且干扰抑制效果随载波频率的改变呈周期性变化。此外，当只考虑强直射径的自干扰抵消并且采用双抽头的干扰抵消结构时，抽头时延与干扰传输时延之差越小或者干扰信号带宽越小，自干扰抑制性能越好。

6 结束语

本文考虑宽带场景下的同时同频全双工系统，讨论了多抽头射频域自干扰抵消结构的抽头参数最优解，并分析了该结构能够实现的最佳自干扰抑制性能，最后以双抽头干扰抵消结构为例，给出了其抽头参数最优解和干扰抑制性能的简化表达式。数值与仿真结果表明，干扰信号带宽越小，多抽头干扰抑制性能越好；且干扰抑制效果随载波频率的改变呈周期性振荡。考虑单径自干扰信号并且采用双抽头干扰抵消结构的简化场景，当干扰传输时延与抽头时延之差越小，或者干扰信号带宽越小时，干扰抑制性能越好。针对宽带场景中的同时同频全双工系统，本文的研究成果可以为其射频域自干扰抵消方案的设计与性能评估提供参考。

[1] DEMESTICHAS P, GEORGAKOPOULOS A, KARVOUNAS D, et al.5G on the horizon: key challenges for the radio-access network[J].IEEE Vehicular Technology Magazine, 2013, 8(3): 47-53.

[2] CIRIK A C, RONG Y, HUA Y. Achievable rates of full-duplex MIMO radios in fast fading channels with imperfect channel estimation[J].IEEE Transactions on Signal Processing, 2014, 62(15): 3874-3886.

[3] ELSAYED A, ELTAWIL A M, SABHARWAL A. Rate gain region and design tradeoffs for full-duplex wireless communications[J]. IEEE Transactions on Wireless Communications, 2013, 12(7): 3556-3565.

[4] 杨吉松, 刘皓, 孙辰. 基于空间投影的全双工 MIMO 中继站自反馈干扰抑制[J]. 通信学报, 2014, 35(9): 156-163.YANG J, LIU H, SUN C. Loop interference suppression based on space projection in full-duplex MIMO relays[J]. Journal on Communications, 2014, 35(9): 156-163.

[5] SABHARWAL A, SCHNITER P, GUO D, et al. In-band full-duplex wireless: challenges and opportunities[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(9): 1637-1652.

[6] CHOI J I, JAIN M, SRINIVASAN K, et al. Achieving single channel,full duplex wireless communication[C]//MobiCom’10, New York,USA, 2010:1-12.

[7] JAIN M, CHOI J, KIM T M, et al. Practical, real-time, full duplex wireless[C]//Mobile Computing and Networking. New York, USA,2011: 301-312.

[8] HONG S, MEHLMAN J, KATTI S. Picasso: flexible rf and spectrum slicing[C]//SIGCOMM’12, Helsinki, Finland. 2012: 13-17.

[9] DUARTE M, DICK C, SABHARWAL A. Experiment-driven characterization of full-duplex wireless systems[J]. IEEE Transactions on Wireless Communications, 2012, 11(12): 4296-4307.

[10] LEE J H. Self-interference cancellation using phase rotation in full duplex wireless[J]. IEEE Transactions on Vehicular Technology, 2013,62(9): 4421-4429.

[11] DUARTE M, SABHARWAL A, AGGARWAL V, et al. Design and characterization of a full-duplex multiantenna system for Wi-Fi networks[J]. IEEE Transactions on Vehicular Technology, 2014, 63(3):1160-1177.

[12] MCMICHAEL J G, KOLODZIEJ K E. Optimal tuning of analog self-interference cancellers for full-duplex wireless communication[C]//2012 50th Annual Allerton Conference on Communication,Control, and Computing. Monticello, Illinois, 2012: 246-251.

[13] ZHANG Z, SHEN Y, SHAO S, et al. Full duplex 2×2 MIMO radios[C]//IEEE 2014 Sixth International Conference on Wireless Communications and Signal Processing (WCSP). Hefei, China, 2014:1-6.

[14] HUUSARI T, CHOI Y S, LIIKKANEN P, et al. Wideband self-adaptive RF cancellation circuit for full-duplex radio: operating principle and measurements[C]//2015 IEEE 81st Vehicular Technology Conference (VTC Spring). Glasgow, 2015: 1-7.

[15] CHOI Y S, SHIRANI-MEHR H. Simultaneous transmission and reception: Algorithm, design and system level performance[J]. IEEE Transactions on Wireless Communications, 2013, 12(12):5992-6010.

[16] KOLODZIEJ K E, MCMICHAEL J G, PERRY B T. Adaptive RF canceller for transmit-receive isolation improvement[C]//2014 IEEE Radio and Wireless Symposium (RWS). Newport Beach, 2014:172-174.

[17] KOLODZIEJ K E, MCMICHAEL J G, PERRY B T. Multi-tap RF canceller for in-band full-duplex wireless communications[J]. IEEE Transactions on Wireless Communications, 2016, 15(6) : 4321-4334.

[18] TURIN G L. Communication through noisy, random-multipath channels[D]. Massachusetts Institute of Technology, 1956.

[19] OPPENHEIM A S, WILLSKY A S, NAWAB S H. Signals and systems[M]. 2nd ed. Upper Saddle River: Prentice Hall, 1996: 164-168.[20] HAYKIN S. Adaptive filter theory[M]. Upper Saddle River: Prentice Hall, 2001: 50-74.

[21] COUCH L.W, Digital and analog communication systems[M]. 5th ed.Upper Saddle River: Prentice Hall, 1997: 179-185.

[22] 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2013: 54-55.ZHANG X D. Matrix analysis and applications[M]. Beijing: Tsinghua University Press, 2013: 54-55.

[23] SALEH A A M, VALENZUELA R. A statistical model for indoor multipath propagation[J]. IEEE Journal on Selected Areas in Communications, 1987, 5(2): 128-137.

[24] FOERSTER J. Channel modeling sub-committee report final[R]. IEEE P802.15-02/490r1-SG3a, 2005.

[25] RAPPAPORT T S. Wireless communications: principles and practice[M]. 2nd ed Prentice Hall,2001.

[26] WEI X S, CRUICKSHANK D G M, MULGREW B. A unified approach to dynamic length algorithms for adaptive linear equalizers[J].IEEE Transactions on Signal Processing, 2007, 55(3): 908-920.

Performance analysis of broadband self-interference cancellation at RF domain in co-frequency co-time full duplex systems

WANG Jun1, ZHAO Hong-zhi1, MA Wan-zhi1, TANG You-xi1, QING Chao-jin2
(1. National Key Lab of Science and Technology on Communication, UESTC, Chengdu 611731, China;2. School of Electrical and Information Engineering, Xihua University, Chengdu 610039, China)

Due to the lack of performance analysis of the RF domain broadband self-interference cancellation algorithms in the co-time and co-frequency full duplex system, the multi-tap RF domain self-interference cancellation structure were considered, and the optimal solutions of its parameters to minimize the residual interference signal power were discussed, then its achievable interference cancellation capability was analyzed. By analysis and simulation, the performance of the multi-tap structure was associated with the interference bandwidth, the carrier frequency,and the differences between the multi-tap delays and multipath delays of the self-interference channel. The greater the signal bandwidth is, or the larger the differences between the multi-tap delays and multipath delays are, the worse the interference cancellation performance is. Besides, the interference cancellation performance is periodic oscillation with the increase of carrier frequency.

wireless communication, co-time and co-frequency full duplex, RF self-interference cancellation, broadband,multi-tap

s: The National Natural Science Foundation of China (No.61531009, No.61501093, No.61271164, No.61471108,No.61201266), The National Major Projects of China (No.2014ZX03003001-002),The Fundamental Research Funds for the Central Universities of China

TN911.7

A

10.11959/j.issn.1000-436x.2016184

2015-11-04；

2016-08-17

国家自然科学基金资助项目（No.61531009, No.61501093, No.61271164, No.61471108, No.61201266）；国家重大专项基金资助项目（No.2014ZX03003001-002）；中央高校基本科研业务费专项资金基金资助项目

王俊（1988-），女，重庆人，电子科技大学博士生，主要研究方向为无线通信信号处理、全双工通信自干扰抑制技术等。

赵宏志（1978-），男，河北石家庄人，博士，电子科技大学副教授，主要研究方向为无线通信信号处理、通信抗干扰技术、并行化通信信号处理等。

马万治（1977-），男，四川都江堰人，博士，电子科技大学助理研究员，主要研究方向为空时编码、MIMO 非相干检测技术、分布MIMO信道建模等。

唐友喜（1964-），男，河南潢川人，博士，电子科技大学教授、博士生导师，主要研究方向为无线通信中的信号处理、嵌入式系统设计等。

卿朝进（1978-），男，四川安岳人，博士，西华大学副教授，主要研究方向为无线网络与通信、压缩感知、可再生能源通信、超奈奎斯特采样、能源感知无线资源管理及分布式天线系统等前沿技术研究。