不可靠链路下基于压缩感知的WSN数据收集算法

张策，张霞，李鸥，梅关林，韩哲，张大龙，刘广怡

（1. 解放军信息工程大学信息系统工程学院，河南 郑州 450001；2. 郑州大学信息工程学院，河南 郑州 450001）

不可靠链路下基于压缩感知的WSN数据收集算法

张策1，张霞1，李鸥1，梅关林1，韩哲1，张大龙2，刘广怡1

（1. 解放军信息工程大学信息系统工程学院，河南 郑州 450001；2. 郑州大学信息工程学院，河南 郑州 450001）

为了解决WSN中基于压缩感知（CS, compressive sensing）的数据收集方法会受不可靠链路影响的问题，首先通过实验对基于CS的数据收集算法中数据重构信噪比与链路误码率的关系进行了定量研究，根据WSN链路分组丢失特性将分组丢失问题分为轻负载和重负载2种情况。针对轻负载下的链路不可靠，建立随机分组丢失模型，并提出了基于邻居拓扑空间相关预测的CS数据收集算法，利用数据空间相关性减小错传的影响。针对重负载下的链路不可靠，建立节点伪失效模型，并提出了基于稀疏调度的CS数据收集算法，通过改变观测矩阵稀疏度，避免观测出错数据，弱化不可靠链路的影响。仿真分析表明，在不增加能耗的前提下有效提高了数据重构质量，降低了不可靠链路对CS数据收集的影响。

无线传感网；数据收集；压缩感知；不可靠链路；空间相关性

1 引言

无线传感网（WSN）正在逐步从实验室走向实际应用，在此过程中，传感网仍受到诸多限制，面临许多挑战：传感器节点通常使用电池作为能源，能源受限；所采集原始数据冗余度高，传输能耗高；节点能耗不均衡，靠近sink的节点能耗快，易形成能量空洞，影响网络寿命；传感网无线链路不可靠，存在较高误码率。

近年来，基于压缩感知的数据收集方法受到研究者的关注[1～3]。将压缩感知理论[4,5]应用于 WSN数据收集中，具有如下优势：第一，有效利用传感器节点所采集的原始信息的空间相关性，减少数据传输能耗；第二，压缩感知数据收集方法具有天然的能耗均衡特性，能降低甚至克服能量洞问题，从而延长网络寿命；第三，相对于分布式数据压缩等传统的压缩方法，该方法具有压缩过程简单而数据重构过程复杂的特点，十分适合传感器节点信息处理能力和能源受限的要求。文献[6]将CS技术与 Pegasis路由协议相结合，在路由链中压缩数据以均衡能耗、延长网络寿命，但是该方法的网络顽健性差。文献[2～7]将CS技术与最小路径树路由协议相结合，以降低整个数据传输路径上的能耗。文献[8]指出，简单地在树形路由中使用 CS，将增加叶节点和距离叶节点较近的中间节点的通信量，针对该问题提出了混合压缩感知(hybrid-CS)数据收集方法，仅对一部分通信量高的父节点使用压缩感知技术，以此减少网络数据通信量。当网络规模较大时，通过分簇构建层次化网络结构，更有助于提高网络数据传输和管理的效率。文献[9]借鉴Leach的思想，在簇内压缩感知模式下计算出全网最优簇首个数，并使簇首均匀分布在全网中，以减少网络能耗。

以上文献都假定传输链路是可靠的，在实际应用场景中，传感器节点被大量布置在森林、火山和战场等环境中[10]，受环境因素、障碍物阻挡、节点布置高度[11]、天线方向[12]、不对称链路[13]和信道冲突堵塞等原因的影响，无线链路不可靠现象普遍存在。

传统的数据收集方法中，一个分组丢失或出错，仅影响单个传感器，然而在分布式压缩感知数据收集中，多个传感器节点采集的信息通过随机观测和求和操作，被合并为一个数据分组，一旦该分组丢失或错传，参与本次压缩感知的所有传感器节点都将受到影响,不可靠无线链路对基于压缩感知的数据收集方法的影响不容忽视，然而，现有研究中对此问题的讨论还很少。文献[14]考虑了树形路由中不可靠链路对压缩感知的影响，分析了分组丢失对数据重构精度的影响。首先根据预先设定的调度概率随机选择出本轮数据收集需要参与的节点，并通过最短路由将这些节点采集数据传输至sink节点，不可靠链路会使其中部分数据丢失。sink根据收到的正确数据分组构造观测矩阵，令观测矩阵每列只有一个非零值，使通过最短路由方式收到的数据即为压缩感知观测值，并构造出与此观测矩阵相对应的稀疏基。最后根据重构精度的高低，动态调整调度概率和观测数，以满足最小重构精度。由于sink根据最终接收到的数据构造观测矩阵，避免观测发生分组丢失的节点，能够抵抗由于不可靠链路对数据收集带来的影响，但其数据分组通过最短路由方式传输，仍然存在网络能耗不均衡问题，且没有考虑被监测网络中事件源对数据相关性的影响。

为此，本文在有事件源发生的传感网中、在不可靠无线链路的条件下，研究了基于压缩感知的数据收集算法。首先，通过实验的方法定量研究了在压缩感知数据收集中，数据重构信噪比，即重构精度，与无线链路误码率的关系；分别针对网络负载较轻、无线链路随机分组丢失和网络负载较重、无线链路由于拥塞连续分组丢失的2种情况，建立无线链路分组丢失模型，并提出了基于邻居拓扑空间相关性预测的压缩感知数据收集算法(CS-NTSC,neighbor topology spatial correlation prediction based CS data gathering)和基于稀疏调度的压缩感知数据收集算法(CS-SSDG, sparse schedule for CS data gathering)，降低不可靠链路对数据收集的影响；最后验证了方法的有效性，实现对不可靠链路中有损数据高精度、低能耗的数据收集。

2 系统模型

本节首先介绍整个网络的数据空间相关性模型，考虑网络内有事件源发生时节点空间相关性并建立模型，介绍了传感网中基于压缩感知的分簇数据收集方法。

2.1 传感网数据空间相关性模型

假设监测区域中有突发事件源发生，如森林中的着火点。用方阵G记录网络中的突发事件源的信号强度，其中，gij表示子区域(i, j)中的事件源的信号强度，表示该子区域中无突发事件源。

本文将方阵转化为向量的形式来表示整个区域中传感器节点和事件源，即

传感网中每个传感器节点采集的信号强度是由网络中Ns个事件源的信号叠加而成的[15]，即

其中，Ψ为传感器感知数据随距离衰减系数矩阵。本文利用欧氏距离的空间相关性模型[16]，假定传感器节点i和j的坐标为和，两节点之间距离为

若在节点i处有事件源发生，节点i接收到信号功率为 Pi，节点j接收到信号功率为Pj，信号按欧氏距离衰减，则有

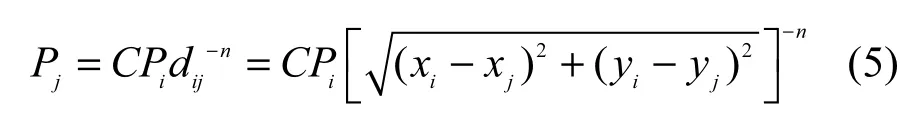
其中，C为常数，n为信号的衰减系数。不同类型的事件源衰减系数不同。2个区域中节点采集到的信息之间的相关性与其欧氏距离成反比，距离越近，衰减系数n越小，节点采集到的信息越接近，相关性越大。本文令

本文研究均基于本节的全网相关性数据模型，提出相关算法。

2.2 基于压缩感知的分簇数据收集方法

假定网络采用分簇结构，以距离事件源最近的节点为簇首，若网络中有Ns个事件源，将整个网络划分为Ns个簇[16]，在每个簇内，使用压缩感知技术进行数据收集，如图1所示，重点研究簇内不可靠链路对基于压缩感知的数据收集方法的影响及相应对策。

假设簇内有N1个成员节点，随机观测矩阵为，其中，M?N1，使用文献[17]中给出的观测矩阵。

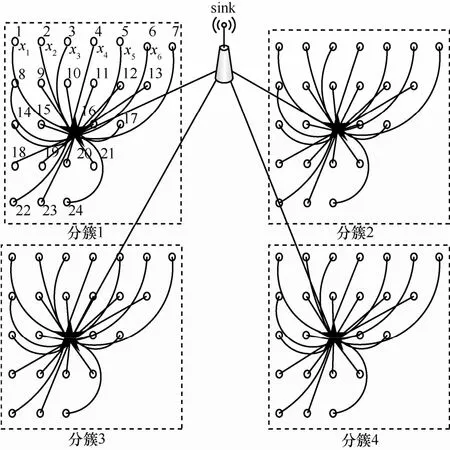
图1 网内分簇数据收集示意

其中，s控制观测矩阵的稀疏程度，p为 3种情况出现的概率。若，则Φ中每一行有个非零

簇首将本簇的观测向量发送至sink，sink根据观测矩阵重构簇内数据，其计算过程可转化为一个求解凸优化问题。

3 不可靠链路对簇内数据收集影响分析

在无线传感网中，链路质量并不完全可靠，因系统噪声和随机噪声等环境因素干扰导致节点间传输数据发生错误。本文通过实验的方法，定量地研究不可靠链路对压缩感知数据收集方法的影响。在有一定误码率的信道中，当节点发送数据分组发生错传时，若接收节点通过信道译码无法恢复发生的错传位，此时接收节点将丢弃错传数据分组，即分组丢失。

在一个簇中使用压缩感知技术进行数据收集，成员节点通过单跳的方式将收集到数据传输到簇首节点，如图1所示，在簇首节点处进行数据观测。假设簇中有N1个节点，在可靠链路下收集数据，没有发生错传时，簇首收到的数据为则观测矢量Y为

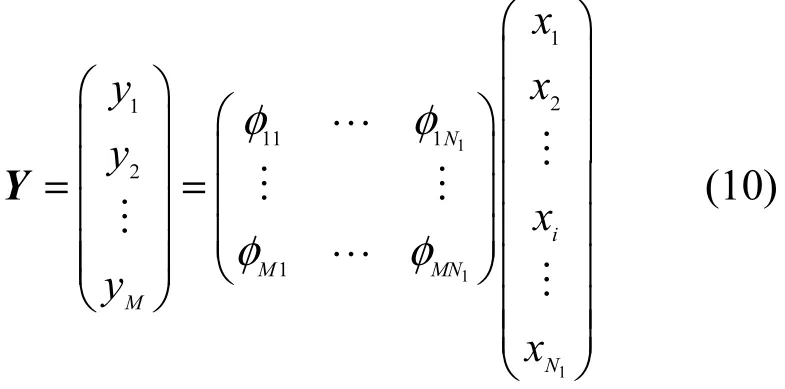
为了评估感知数据恢复质量，本文用重构数据信噪比来衡量数据重构精度，定义为

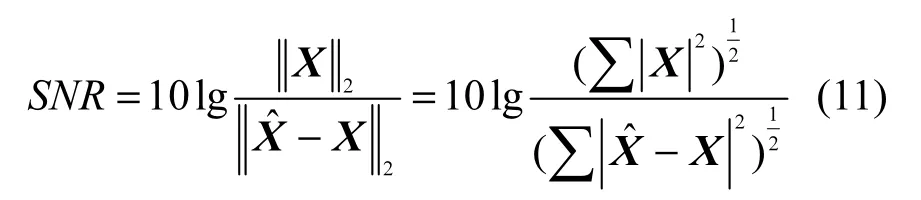
由式(9)可知，X为原数据，Xˆ为重构数据，重构信噪比越高，算法性能越好。图2给出了观测次数M与数据重构信噪比的关系，仿真中假定簇内有 900个节点，一个事件源，衰减系数n=0.01且误码率Pb=0。随着M的增加，重构数据信噪比也在增加，当Mgt;450后，信噪比趋于平稳。由于不同的用户对重构数据信噪比要求不尽相同，相应的M也不同。为了便于比较，在后续的仿真实验中，本文选取作为比较基准，由图2可得此时M=450。

图2 观测次数与信噪比关系

此时，由于一个节点的发送数据发生错误，导致观测向量Y′中每一个观测值都受到了影响。图3所示为当观测次数M=450时，不同误码率对簇内压缩感知数据重构精度的影响，在高误码率环境中，重构数据信噪比远远低于无误码情况下的重构信噪比36.16 dB；随着误码率的减小，重构精度也在增加。在实际的无线传感网中，链路质量十分不可靠，且误码率较高，此时利用压缩感知收集到的数据进行重构，会得到低精度甚至无用的数据。

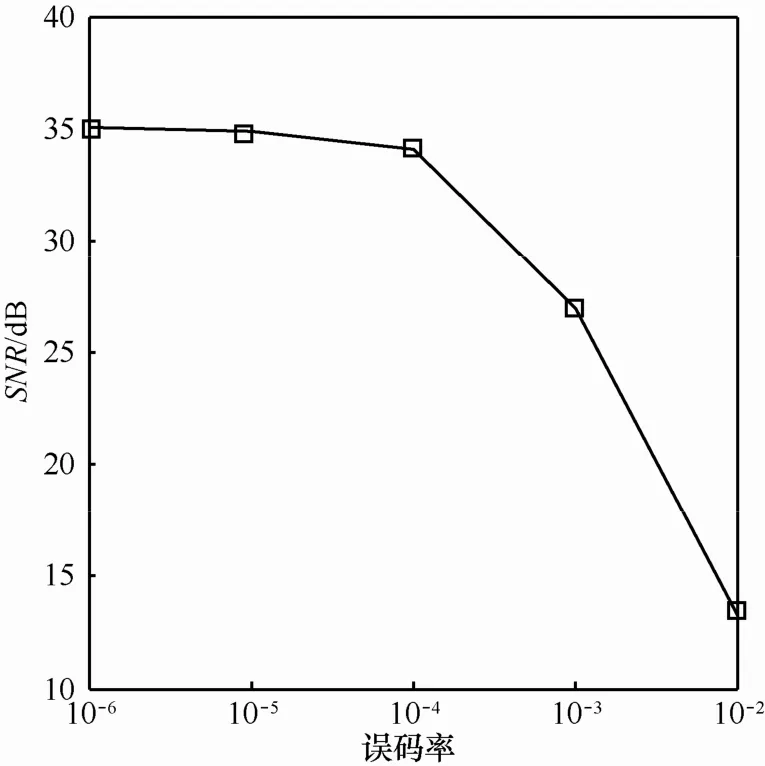
图3 误码率对重构精度影响

进一步分析给定误码率条件下不同比特发生错误对重构信噪比的影响。若传感器节点将采集到的数据转换成8 bit二进制符号进行传输，即第i个节点采集到数据为

图4 错误发生位数对重构精度影响

由以上仿真实验可知，不可靠链路对分布式压缩感知数据收集有一定影响，当误码率较低，错误位发生在低位时，重构精度受影响程度小；在误码率较高的信道环境和错误位发生在高位时，数据重构精度会大幅降低，甚至无法使用。下面针对受不可靠链路影响较大的情况开展研究，建立相应的分组丢失模型和数据收集算法，给出对策。

4 分组丢失模型建立

传感网中当节点采集数据和回传频率低时，单个节点数据分组发送任务减少，全网负载轻；当节点采集数据和回传的频率高，单个节点数据分组发送任务增多，全网负载加重，网络易发生拥塞。基于传感网负载轻重与文献[18]中多种分组丢失模型，本文将分组丢失分成如下2种情形。第一种情况考虑网络轻负载、有随机干扰或噪声，此时节点在每个数据传输周期随机分组丢失；第二种情况考虑网络局部突然产生大量负载、链路存在噪声和拥塞，此时节点会在多个相邻数据传输周期连续分组丢失。分别针对以上2种情形，总结出2种分组丢失模型：随机分组丢失模型和节点伪失效模型。

在误码率为Pb的无线信道中，假设节点 A发送一个Lbyte的数据分组，则数据分组成功发送的概率为

4.1 随机分组丢失模型

若网络没有发生拥塞，且每个节点在每个时刻发生分组丢失是独立随机的，即在一轮数据收集发生错传后，下一轮数据收集并不受影响，本文将这种分组丢失模型称为随机分组丢失模型，如图5(a)所示，该模型一般由环境噪声和信道冲突造成的，单个节点在第t轮数据收集时数据分组成功发送概率为

根据节点随机丢失发送数据的特点，可以利用邻居节点之间的空间相关性“合成”A节点采集数据的预测值。

4.2 节点伪失效模型

若网络发生拥塞，节点A在t轮数据收集分组丢失后，在t+1轮数据收集时则有更大概率分组丢失，即在一段时间内节点如同失效，不能成功收发数据，会影响多轮的数据收集，本文将这种分组丢失模型称为节点伪失效模型，如图5(b)所示，该模型下单个节点在第t轮数据收集时数据分组成功发送概率为

图5 分组丢失模型示意

5 算法设计

本节分别针对以上 2种分组丢失模型，提出CS-NTSC算法和CS-SSDG算法。由于在链路可靠性较低的情况下，重传不仅会带来极大的通信开销与传输时延，而且在有些情况下可能恶化系统性能[19],本文所提算法均设定在不重传的前提下来提高数据重构精度，减小误差。

5.1 CS-NTSC算法

针对随机分组丢失模型，根据对数据空间相关性特性的分析，提出基于邻居拓扑空间相关性预测的压缩感知数据收集算法。

在传感网中，传感器节点通常可以根据距离来判断节点是否在自己邻居范围内，假设此范围为引入矩阵即令距离，。若第ke个节点发生错传，则令矩阵A的第ke列为0

矩阵A表示节点与其邻居节点的相关性，利用节点之间的距离表示相关性强弱。若节点z0与邻居节点z1距离较近，则其相关性强，较大；若节点z0与邻居节点z1距离较远，则其相关性弱，较小；若节点z0的邻居节点z1发生错传，则其相关性为0，即

其中，X*(i,1)为经过邻居拓扑矩阵处理后的节点i的采集数据，丢弃节点i的错传数据，利用邻居节点的空间相关性，矩阵H保证了相关性强的节点权值大，相关性弱的节点权值小，合成估计值，使由式(19)可知，错传节点i对应的矩阵H中第i列为0，所以错传节点i并不参与其需要估计的邻居节点的估计。由X*与观测矩阵Φ可得观测向量Y*。

通过Y*重构X，如式(23)，具体数据算法如算法1所示。

算法1 CS-NTSC算法

1) 簇首收到整个簇的邻居矩阵A;

4) if 第 xi′个数据分组有错

7) end for

8) Ω←i /* 记录错误节点号的索引*/;

该算法的复杂度为O(N1)，簇首只需在首次数据传输前，根据网络中节点布设拓扑结构获取矩阵A，在每轮数据传输时根据错传节点号和矩阵A得到邻居拓扑矩阵H；在数据处理时，簇首只需做简单的乘、加线性运算，无大量复杂运算，最终快速得到本簇观测向量，具有实时性。

5.2 CS-SSDG算法

当网络发生拥塞时，网络一定范围内的多个节点均会发生伪失效，即伪失效节点与邻居节点均会传输数据失败，此时无法利用其空间相关性。针对节点伪失效模型，提出基于稀疏调度的压缩感知数据收集算法，通过改变观测矩阵的稀疏度，避免观测错误或丢失的数据，弱化错传和分组丢失对整体信息采集的影响，利用信息之间的相关性，重构原始数据。

假设观测矩阵Φ为

当第r个节点发生伪失效时，令Φ(r)=0，即第r列置为0，改变观测矩阵的稀疏度，则

每轮数据收集时，并没有对节点r进行观测，对数据重构起作用的是其他没有发生分组丢失的节点，第i个观测值yi如式(26)，此时将节点r对数据重构的影响降到了最低。当sink节点用矩阵Φ*进行数据重构时，即可重构出原始数据，具体数据收集算法如算法2所示。

算法2 CS-SSDG算法

3) if 节点r发生伪失效

5) end if

6) end for

7) for i=1:M

9) end for

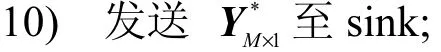
11) end if

由算法 2可知，该算法的复杂度为O(N1)，且簇首可根据收到的数据实时计算观测矩阵Φ*，相关运算均为简单的线性运算，具有实时性与可使用性。

5.3 网络负载判断机制

簇首根据节点传输数据的历史情况，来判断网络负载情况，进而确定当前采用 CS-SSDG还是CS-NTSC算法。具体判断策略如下：在首轮数据收集中，假设网络没有发生拥塞，即网络运行在轻负载下，节点的分组丢失模型为随机分组丢失模型。簇首在收集数据的同时，记录并存储数据传送失败的成员节点号；若在连续3个数据收集周期内均传输失败的节点个数超过本簇内成员节点总数的，此时簇首即认为网络内负载变重，节点分组丢失模型为节点伪失效模型。簇首判断网络负载具体流程如下。

3) if 第 xi′个数据分组有错

4) Ωt←i /* 记录第 t轮错误节点号的索引*/;

5) end if

6) end for

7) j=0;

8) end if

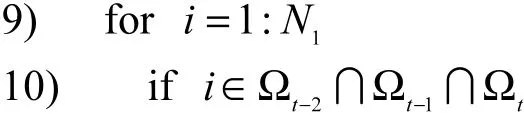
11) j=j+1;

12) end if

13) end for

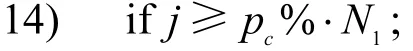
15) 簇首使用CS-SSDG算法;

16) else 簇首使用CS-NTSC算法;

17) end if

当簇首判断网络是重负载时，则簇首采用CS-SSDG算法；若在连续3个数据收集周期内均传输失败的节点个数少于本簇内成员节点总数的，则重新采用CS-NTSC算法。网络算法流程如图6所示。

6 仿真与分析

为了验证算法的有效性，在 MATLAB平台下进行仿真分析，仿真环境设置如下：在一个簇内，簇成员节点通过单跳将数据传输给簇首，由簇首进行数据压缩，将观测矩阵发送给sink节点，在sink处进行数据重构，发送数据分组长度为10 byte；设定簇内有 900个节点随机均匀分布在30×30区域内，簇内有一个事件源，其衰减系数n=0.01，观测次数M=450；采用正交匹配追踪算法(OMP,orthogonal matching pursuit)作为重构算法。

本文假设在有一定误比特率的无线信道中，簇首接收到有误码的数据分组时不重传，利用一轮重构数据精度作为算法性能指标；同时，还将所提方法与基本的压缩感知数据收集(CDG, compressive data gathering)算法[2]和 SRS-DG (sparsest random scheduling based CDG scheme)算法[14]对比。文献[2]中传统CS数据收集算法利用压缩感知技术收集并重构数据，并不考虑误比特率对算法的影响，文献[14]中SRS-DG算法考虑到链路中存在分组丢失，利用构造的极稀疏矩阵（sparsest measurement matrix）观测无错数据。

6.1 CS-NTSC算法仿真与分析

6.1.1 CS-NTSC算法性能分析

当事件源衰减系数n=0.01，邻居范围RThr=2时，CS-NTSC算法性能如图7所示。在误码率较小时，3种算法性能接近；当误码率较高为时，CS-NTSC算法具有较好的性能，由图7可知，此时CDG算法的重构数据信噪比为27.33 dB，高误码率对CDG算法具有较大的影响；SRS-DG算法的数据信噪比为29.72 dB，由于SRS-DG算法是针对分组丢失设计的算法，数据分组一旦有错传即丢弃，利用稀疏观测矩阵观测无错节点，导致每次数据观测信息量减少，该算法通过下一轮数据收集增加观测数来弥补丢失的数据分组，提高重构信噪比，因此，本轮数据重构信噪比并不高；CS-NTSC算法得到重构数据信噪比为35.91 dB，在一定条件下利用数据的空间相关性预测错传数据，避免丢弃使信息量减少。因此，在高误码率的无线环境中，CS-NTSC算法没有增加额外的通信能耗，能够克服错传数据分组对数据重构的影响，具有有效性。

图6 网络算法流程

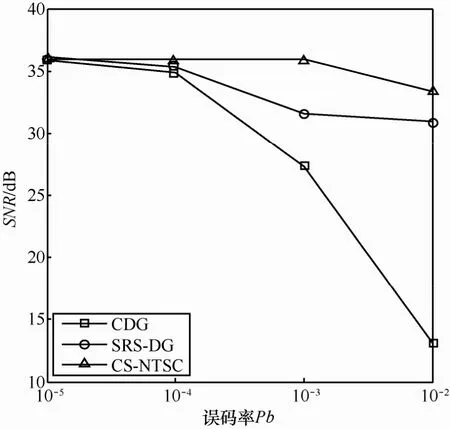
图7 CS-NTSC算法性能

6.1.2 影响CS-NTSC算法因素分析

CS-NTSC算法利用了节点之间的空间相关性以降低不可靠链路对压缩感知数据收集的影响，所以事件的衰减系数n、邻居范围RThr和数据分组长度都会影响 CS-NTSC的性能，下面通过仿真讨论上述因素对算法性能的影响。

由于事件源的衰减系数n会影响全网数据的空间相关性，所以衰减系数会影响 CS-NTSC算法性能，如图8所示，为数据分组为10 byte时，衰减系数n与SNR的关系。当衰减系数较小时，即事件源的影响范围大，此时全簇的节点均较大程度地受到事件源影响，节点空间相关性强，在邻居范围内，节点与节点采集数据接近，CS-NTSC算法性能好；当衰减系数较大时，即事件源的影响范围小，距离事件源较远节点受到影响小，全簇节点的空间相关性弱，CS-NTSC算法性能较差。当ngt;0.5，此算法的数据重构精度变差。

图8 衰减系数与重构信噪比的关系

邻居范围RThr也会影响算法性能，如图9所示，为信噪比和衰减系数不变时，RThr与SNR的关系。随着RThr的增大，节点的邻居节点数会随之增加，在事件源影响范围不变的情况下，RThr过大会使邻居节点之间的空间相关性减小，CS-NTSC算法性能变差，算法不再适用。

图9 邻居范围与重构信噪比关系

信道误码率一定时，数据分组越长，会使网络的分组丢失率越高。图10反映了时，分组长与数据重构精度的关系。由图可知，在n较小，分组长较短的情况下，由于网络节点空间相关性强，分组丢失率低，此时 CS-NTSC算法的数据重构精度高；当n增大，分组长变长时，节点空间相关性弱，分组丢失率高，此情况下CS-NTSC算法性能变差，不再适用。

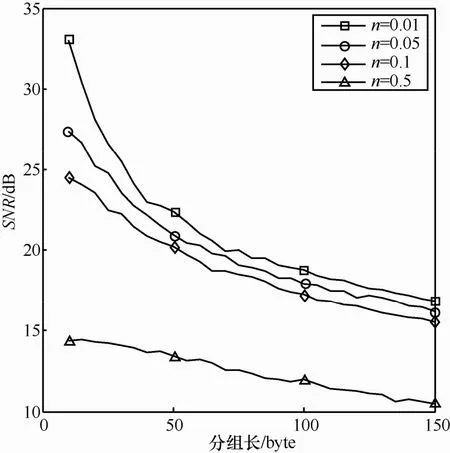
图10 分组长与重构信噪比的关系（CS-NTSC）

由以上仿真结果可以得出，当网络中事件源衰减系数较小，邻居范围小且数据分组短时，CS-NTSC算法能够在不分组丢失也不重传的情况下，抵抗不可靠链路对数据重构的影响，以较高精度重构出数据，性能优势明显。

6.2 CS-SSDG算法仿真与分析

图11 CS-SSDG算法性能

图12 分组长与重构信噪比的关系（CS-SSDG）

7 结束语

本文针对链路不可靠的无线传感网，首先利用仿真的方法，详细分析了不可靠链路对簇内压缩感知数据收集的影响，误码较高的信道环境对压缩感知数据收集具有很大影响。根据真实网络提出2种分组丢失模型，针对随机丢失模型，提出了CS-NTSC算法，分析了网络中的空间相关性，并利用空间相关性和邻居拓扑矩阵对发生错传的数据进行估计，减小错误幅度。讨论了衰减系数和邻居范围对 CS-NTSC算法的影响，算法在衰减系数小和邻居范围小时，重构精度更高；针对节点伪失效模型，提出了 CS-SSDG算法，将发生失效节点的相关观测列向量置为 0，来避免收集发生失效的节点数据，只收集完整正确的数据，以减小错传或分组丢失对整个数据收集和重构的影响。仿真结果表明，CS-NTSC算法与CS-SSDG算法能够在高误码率的环境中高精度重构出数据，具有有效性。

本文分别针对轻负载、随机分组丢失和重负载、伪随机失效2种情况研究了不可靠链路下的压缩感知数据收集算法，并简单讨论了2种算法的切换条件。然而在实际传感网中，节点分组丢失模型可能会出现2种分组丢失模型的混合，如何将算法有效地应用于混合分组丢失模型下，是下一步研究的重点。

[1] RABBAT M, HAUPT J, SINGH A, et al. Decentralized compression and predistribution via randomized gossiping[C] //The 5th Int Conf on Information Processing in Sensor Networks. New York: ACM, 2006: 51-59.

[2] LUO C, WU F, SUN J, et al. Compressive data gathering for large-scale wireless sensor networks[C] //The 15th Annual Int Conf on Mobile Computing and Networking. New York: ACM, 2009: 145-156.

[3] WANG J, TANG S, YIN B, et al. Data gathering in wireless sensor networks through intelligent compressive sensing[C]// IEEE INFOCOM 2012. Piscataway, NJ: IEEE, 2012: 603-611.

[4] DONOHO D L. Compressed sensing[J]. IEEE Trans on Information Theory, 2006, 52(4): 1289-1306.

[5] BARANIUK R. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 56(4): 4-5.

[6] OSAMY W, SALIM A, AZIZ A. Efficient compressive sensing based technique for routing in wireless sensor networks[J]. Infocomp Journal of Computer Science, 2013, 12(1): 1-9.

[7] LUO C, WU F, SUN J, et al. Efficient measurement generation and pervasive sparsity for compressive data gathering[J]. IEEE Trans on Wireless Communications, 2010, 9(12): 3728-3738.

[8] LUO J, XIANG L, ROSENBERG C. Does compressed sensing improve the throughput of wireless sensor networks?[C]// IEEE Int Conf on Communications (ICC 2010). New York: IEEE Communications Society, 2010: 1-6.

[9] WU X, XIONG Y, HUANG W, et al. An efficient compressive data gathering routing scheme for large-scale wireless sensor networks[J].Computers amp; Electrical Engineering, 2013, 39(6): 1935-1946.

[10] AKYILDIZ I F, SU W, SANKARASUBRAMANIAM Y, et al. Wireless sensor networks: a survey[J]. Computer Networks, 2002, 38(4):393-422.

[11] NDZI D L, ARIF M A M, SHAKAFF A Y M, et al. Signal propagation analysis for low data rate wireless sensor network applications in sport grounds and on roads[J]. Progress in Electromagnetics Research, 2012,125(17):1-19.

[12] AHMED N, KANHERE S S, JHA S. Utilizing link characterization for improving the performance of aerial wireless sensor networks[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(8): 1639-1649.

[13] BACCOUR N, KOUBAA A, MOTTOLA L, et al. Radio link quality estimation in wireless sensor networks: a survey[J]. ACM Transactions on Sensor Networks, 2012, 8(4):688.

[14] WU X, YANG P, JUNG T, et al. Compressive sensing meets unreliable link: sparsest random scheduling for compressive data gathering in lossy WSN[C]//The 15th ACM Int Symposium on Mobile Ad Hoc Networking and Computing. New York: ACM, 2014: 13-22.

[15] 唐亮, 周正, 石磊, 等. 基于 LEACH 和压缩感知的无线传感网目标探测[J]. 北京邮电大学学报, 2011, 34(3): 8-11.TANG L, ZHOU Z, SHI L, et al. Source detection in wireless sensor network by leach and compressive sensing[J]. Journal of Beijing University of Posts amp; Telecommunications, 2011, 34(3): 8-11.

[16] 张策, 张霞, 李鸥, 等. 基于CS的无线传感网动态分簇数据收集算法[J/OL]. http://crad.ict.ac/cn/CN/abstract/abstract3059.shtml.ZHANG C, ZHANG X , LI O, et al. Data gathering using dynamic clustering based on WSN compressive sensing algorithm[J/OL].http://crad.ict.ac/cn/CN/abstract/abstract3059.shtml.

[17] WANG W, GAROFALAKIS M, RAMCHANDRAN K. Distributed sparse random projections for refinable approximation[C] //The 6th Int Conf on Information Processing in Sensor Networks. New York: ACM,2007: 331-339

[18] KONG L, XIA M, LIU X Y, et al. Data loss and reconstruction in sensor networks[C]// IEEE INFOCOM 2012. Piscataway, NJ: IEEE,2013: 1654-1662.

[19] WU L, YU K, DU T, et al. Efficient information transmission under lossy WSNs link using compressive sensing[C] //2014 IEEE 9th Conference on Industrial Electronics and Applications (ICIEA). NJ: IEEE,2014:493-498.

Compressive sensing based data gathering algorithm over unreliable links in WSN

ZHANG Ce1, ZHANG Xia1, LI Ou1, MEI Guan-lin1, HAN Zhe1, ZHANG Da-long2, LIU Guang-yi1
(1. School of Information Systems Engineering, PLA Information Engineering University, Zhengzhou 450001, China;2. School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China)

To solve the problem that the ubiquitous unreliable links in the WSN influence the performance of the compressive sensing (CS) based data gathering, first the relationship between the reconstruction SNR of CS-based data gathering algorithm and the bit-error-ratio (BER) were simulated quantitatively. Then classify two cases were classified,namely light-payload and heavy-payload, relying on the analysis of wireless link packet loss characteristics. The random packet loss model was conceived to describe the packet loss under light-payload scenario. Further the neighbor topology spatial correlation prediction-based CS data gathering (CS-NTSC) algorithm was proposed, which utilized the nodes spatial correlation to reduce the impact of error. Additionally, the node pseudo-failure model was conceived to describe the packet loss occurred in network congestion, and then the sparse schedule-aided CS data gathering (CS-SSDG) algorithm were conceived, for the purpose of changing the sparsity of measurement matrix and avoiding measurements amongst the nodes affected by unreliable links, thus weakening the impact of error/loss on data reconstruction. Simulation analysis indicates that the proposed algorithms are not only capable of improving the accuracy of the data reconstruction without extra energy, but also effectively reducing the impact affected by the unreliable links imposed on CS-based data gathering.

WSN, data gather, compressive sensing, unreliable link, spatial correlation

The National Science and Technology Major Projects of China (No.2014zx03006003)

TP393

A

10.11959/j.issn.1000-436x.2016185

2016-01-24；

2016-08-05

国家科技重大专项基金资助项目（No.2014zx03006003）

张策（1991-），男，四川南充人，解放军信息工程大学博士生，主要研究方向为无线自组织网络、无线传感网与路由协议。

张霞（1979-），女，山东济南人，博士，解放军信息工程大学讲师，主要研究方向为无线传感网、信息处理与流量识别。

李鸥（1961-），男，陕西宝鸡人，博士，解放军信息工程大学教授、博士生导师，主要研究方向为无线传感网、认知无线电网络与无线自组织网络。

梅关林（1989-），男，四川泸州人，解放军信息工程大学硕士生，主要研究方向为无线通信、卫星调度。

韩哲（1991-），男，河南洛阳人，解放军信息工程大学硕士生，主要研究方向为无线通信、无线传感器网络。

张大龙（1976-），男，河南郑州人，博士，郑州大学讲师，主要研究方向为无线通信、无线传感网与MAC协议。

刘广怡（1982-），男，河南郑州人，博士，解放军信息工程大学讲师，主要研究方向为传感网、智能算法、网络数据分析与物联网。