数与式巧思妙解集锦（一）

朱适宜

数与式巧思妙解集锦（一）

朱适宜

例1一个纸环链，纸环按红黄绿蓝紫的顺序重复排列，截去其中的一部分，剩下部分如图所示，则被截去部分纸环的个数可能是（）.

A.2010B.2011

C.2012D.2013

【解析】本题先找到纸环排列的规律：红、黄、绿、蓝、紫，前部分的最后是红黄绿，那么它的后面必然有蓝紫，后部分是黄绿蓝紫，那么它的前面必然有红.这样被截取的部分是这样排列的：蓝紫红黄绿蓝紫红黄绿蓝紫……红黄绿蓝紫红，中间部分是红黄绿蓝紫的循环.这样截取的纸杯是5n+3，即被5除余数是3的数，故选D.

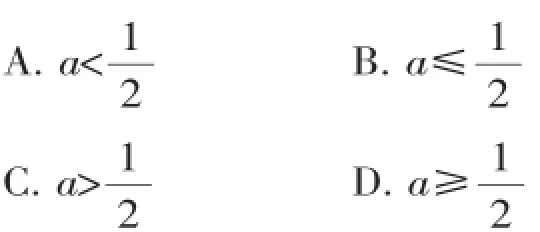
【解析】本题在处理上有两种方法：

第一种：把2a-1看成一个整体，1-2a是 2a-1的相反数，根据

由绝对值为其相反数的数是：负数和0，得：2a-1≤0，a≤

第二种：根据绝对值具有非负性，即结果一定不小于0.

故选B.

例3如下表，从左到右在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等，则第2011个格子中的数为（）.

A.3B.2C.0D.-1

【解析】本题首先要理解其中任意三个相邻格子中所填整数之和都相等的意思，我们可以进行这样的推导：

设有这列数为：a1，a2，a3，a4，…，an，

由题意知：

a1+a2+a3=a2+a3+a4，两边都减去a2+a3，得a1=a4；

a2+a3+a4=a3+a4+a5，两边都减去a3+a4，得a2=a5；

同理可得：a3=a6；a4=a7；a5=a8；……

实际上我们得到的是这样的一组数：

a1，a2，a3，a1，a2，a3，a1，a2，a3，……

则：c=a1=3，a=a5=-1，b=a9=2，

所以这组数是3，-1，2，3，-1，2，3，-1，2，…

2011÷3=670……1，

a2011=a1=3.故选A.

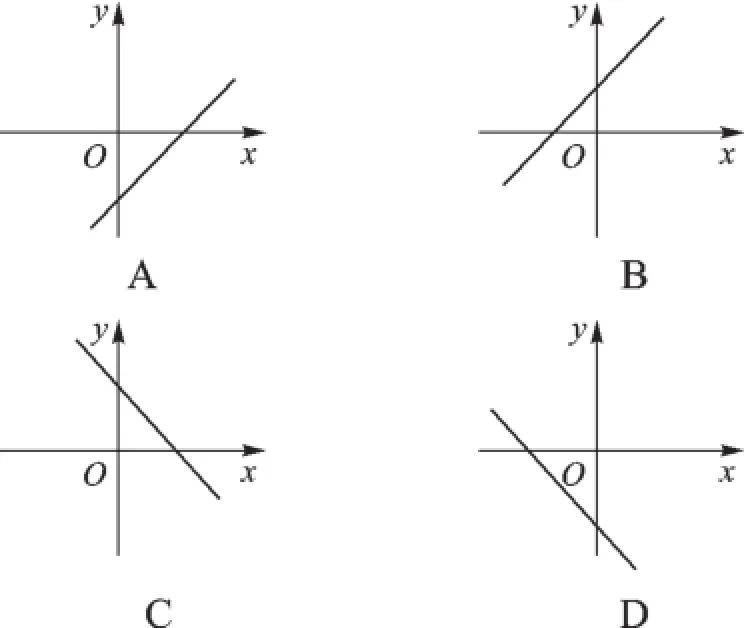
【解析】首先根据二次根式中的被开方数是非负数，以及a0=1（a≠0），判断出k的取值范围，然后判断出k-1、1-k的正负，再根据一次函数的图像与系数的关系，判断出一次函数y=（k-1）x+1-k的图像可能是哪个即可.

解得k＞1，

∴k-1＞0，1-k＜0，

故一次函数y=（k-1）x+1-k的图像必然经过一、三、四象限.故选A.

解法一：

解法二：

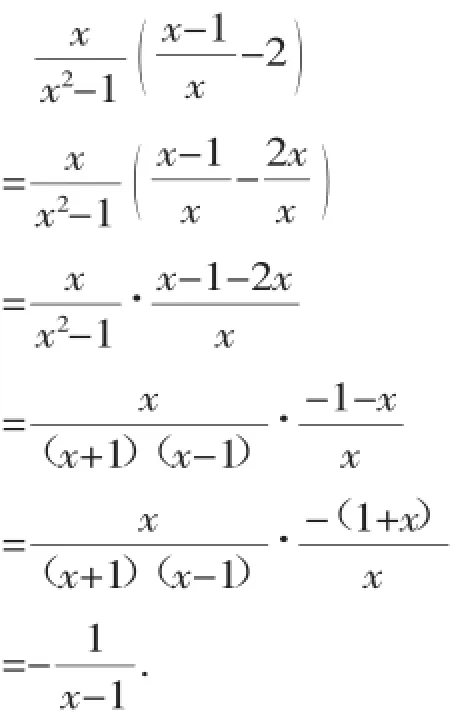
（作者单位：江苏省淮安外国语学校）