河道岸滩稳定性综合评价方法

王延贵，齐梅兰，金亚昆

（1.国际泥沙研究培训中心，北京 100048；2.北京交通大学土木建筑工程学院，北京 100044）

河道岸滩稳定性综合评价方法

王延贵1，齐梅兰2，金亚昆2

（1.国际泥沙研究培训中心，北京 100048；2.北京交通大学土木建筑工程学院，北京 100044）

为了评价河岸边界条件和河流动力条件对岸滩稳定性的影响，以河道岸滩崩塌影响因子层次结构模型和权重系数为基础，将定性指标定量化和定量指标标准化，构造了枯水期和洪水期岸滩稳定综合评价函数，提出了考虑多种因素影响的岸滩稳定性综合评价方法。对拟定的3种不同土壤性质、边界条件和水动力条件的河段岸滩稳定性评价结果表明，岸滩稳定性综合评价过程和评价方法是合理的。

河道；岸滩稳定性；崩岸；层次分析法；综合评价方法

在天然冲积河流演变过程中，崩岸是一种普遍存在的自然现象，国内外主要河流都存在严重的崩岸问题［1-5］，如中国的长江中下游和黄河下游河道、美国的Ohio河、西非的Niger河和澳大利亚的Lockyer Valley。崩岸往往会给河流防洪、岸边建筑物安全等造成严重威胁，特别是近些年来随着大型水利工程的建设或运行，河势将发生明显变化，崩岸强度会有所增强，如三峡水库蓄水运用以来，长江中下游河道发生崩岸655次，崩岸强度有增大的趋势［5］。因此，开展河流岸滩稳定性监测与综合评估就显得极为重要，通过监测和评估可以及时掌控河流岸滩安全状态的变化，从而采取相应的防护措施。

不同河段岸滩水流边界条件存在差别，对应的岸滩稳定性和崩塌机理也不一样。有许多学者就岸滩稳定性和崩塌机理进行了研究［3-4，7-8］，还有一些学者利用数学方法对岸滩安全性进行了分析［9-11］。王坤［9］运用模糊决策理论对不同断面崩岸危险程度进行了评价；廖小永等［10］采用模糊统计聚类理论，建立了以岸滩安全程度为聚类标准的隶属函数，判断得到石首河段不同断面岸滩的安全程度；笔者［11-12］也利用层次分析法对崩岸主要影响因素的作用与权重进行了分析。本文在前期研究的基础上，建立河道岸滩安全性评估的层次结构模型，考虑专家建议推求各影响指标的权重，进而通过模糊数学方法将影响指标进行量化处理，构造岸滩稳定综合评价函数，并对拟定的不同河段稳定性进行评估。

1　岸滩稳定性层次结构模型与影响指标权重

1.1岸滩稳定性的层次结构模型

对河道岸滩安全性进行综合评价时，选取岸滩稳定性作为目标，列为第一层，即目标层。河流崩岸是来水来沙条件和河岸边界条件等诸多因素共同作用的结果，故将崩岸影响因素分为河岸边界条件和河流动力条件两大类，列为第二层。河岸边界条件包括土壤特性和岸坡形态，主要的影响因子有土壤黏聚力、内摩擦角、干密度及边坡形态。河流动力条件主要为来水来沙条件，而来水来沙条件对河道的作用具体表现为河道冲刷，包括河岸侧向冲刷和河床垂向冲刷两个方面。另外，河流的水位变化及洪水浸泡也对崩岸有重要的影响，而洪水浸泡主要是通过对河岸浸泡时间长短来影响崩岸。因此，河岸侧向冲刷、河床垂向冲刷、水位变化、河岸浸泡时间4个因子作为河流动力条件中的分析对象。层次分析结构模型如图1所示。

图1　岸滩稳定性评价层次结构模型

1.2不同时期岸滩稳定性影响因子权重

由于河道水位高低变化与岸滩浸泡状况有很大的差异，河岸稳定性也将随之发生变化。在汛期，河道水位较高，且变化幅度较大，对岸滩浸泡作用明显，河道岸滩崩岸往往会发生在汛末水位迅速降低过程中或之后。长江中下游崩岸90%以上发生在枯水期或汛后，美国密西西比河下游大多数崩岸也发生在汛后，尤以大水年之后崩岸明显。在枯水期，河道水位较低，河道侧向冲刷明显，特别是弯道凹岸崩塌严重。显然，枯水期和洪水期河流岸滩崩塌过程中各影响因子的作用是不一样的，相应的权重也随之发生改变，进而影响岸滩安全性的综合评价。因此，利用层次分析法分别对洪水期和枯水期河流崩岸的影响因子进行分析，对各层次中诸影响因子两两比较，考虑它们之间的相对重要性，列出判断矩阵，进行岸滩安全性影响分析，求得枯水期和洪水期条件下岸滩稳定性各影响因子的权重系数［11-14］，如表1所示，相应也就得到对应枯水期和洪水期各影响因子的权重矩阵W1、W2：

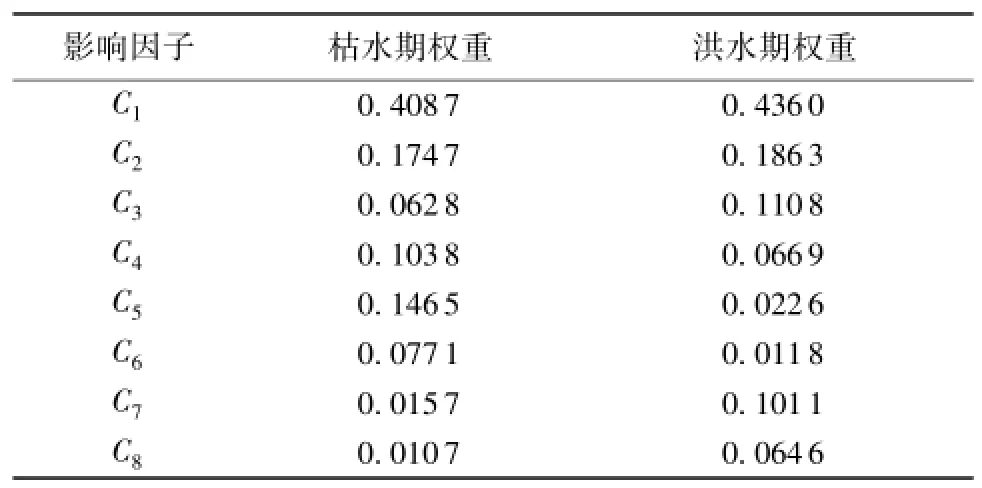
表1　河道岸滩稳定性影响因子权重［12］

2　岸滩稳定性影响因子的量化分析

2.1主要影响因子的量化分析方法

由于岸滩崩塌影响因子的量纲是不同的，很难有效地利用多目标函数评价不同条件下岸滩的稳定性，因此，对岸滩影响指标进行无量纲化处理是非常必要的。河道岸滩安全性影响指标可分为定量指标和定性指标，如与土壤特性相关的黏聚力、内摩擦角、干密度等皆为定量指标，具有准确的数值；河道冲刷（侧向、垂向）、水位变化和河岸浸泡时间等虽然为定量指标，但需要给出进一步的说明。如：侧向冲刷宽度为某河段在某一时期内侧向冲刷的距离，垂向冲刷深度为某河段在某一时期内河床垂向冲刷的深度；水位变化则是某河段在某一时期内水位变化的幅度；河岸浸泡时间为某河段在某一时期内河岸持续浸泡的时长。

对于定量指标，某些指标值越大，岸滩越安全，为正向指标，如土壤黏性系数、土壤内摩擦角；反之，为负向指标，如土壤干密度、河岸侧向冲刷、河床垂向冲刷、河道水位变化、河岸浸泡时间。为便于分析，本文统一约定指标值大者为优（即正向指标），对指标值小为优者（即负向指标）可利用指标同趋势化方法进行处理，形成统一的正向指标。所谓指标同趋势化就是将指标通过整理变换［15］，使所有指标转化为同一方向，具体可采用指标转置的方法处理，计算公式为

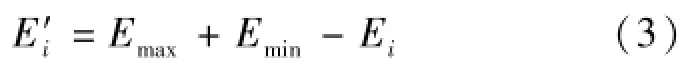
式中：E′i为处理后的正向指标值；Emax为负向指标最大值；Emin为负向指标最小值；Ei为原负向指标值。

指标进行同趋势化处理后，为了消除各指标量纲的影响，需要对指标进行规范化或无量纲化处理，具体方法就是用同一指标数列中的最大值去除数列中的每一个指标值，即

式中：Eii为处理后的无量纲指标值；Emax为正向指标序列中的最大值；Ei为正向序列中第i个指标。

岸滩边坡形态作为一个定性指标，只有定性描述或简单的等级划分，而没有定量数值。为了进一步探讨河岸形态对河岸稳定的影响，通过分析不同类型岸滩边坡形态（图2）的稳定状况，引入岸滩边坡形态坡度参数［16］：

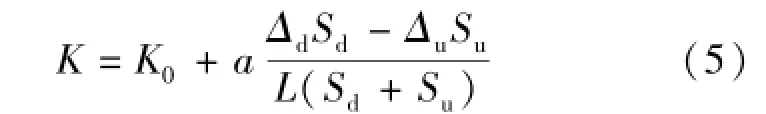
式中：K为岸滩边坡形态坡度；K0为直线岸坡的坡度；Δu、Δd分别为岸坡上部凸出或凹进的厚度（凹进取负值），即图2中的EF和HI；Su、Sd分别为岸坡上部凸出或凹进部分面积（凹进取负值）；L为直线岸坡的坡长，即图2中的AB段；a为岸坡坡度有效系数。一般说来，岸滩边坡形态坡度小于稳定坡度时，岸滩处于稳定状态；当岸滩边坡形态坡度介于崩塌坡度和稳定坡度之间时，岸滩处于不稳定状态；当岸滩边坡形态坡度大于崩塌坡度时，岸滩崩塌。

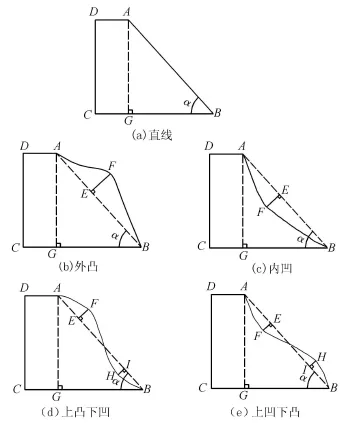
图2　岸滩边坡形态类型

岸滩边坡形态这类指标现阶段还很难用准确的数值表示，仍通过模糊评判法对定性指标进行量化处理，具体方法是根据相关专家对所给定的指标按规定的评语进行评判，并赋予指标隶属度。指标评语集V为

赋予指标评语的隶属度集U为

根据专家对各个指标不同方案下所给的评语，按其标准隶属度进行平均，取平均值作为该指标的隶属度。

2.2岸滩稳定性影响因子的指标量化

为便于分析比较和实际应用，结合河流岸滩边坡形态、土壤特性和水流条件的实际情况，设计了河段土体性质和水位变化差异较大的3个不同河段进行稳定性评估，3个河段分别称为河段1、河段2和河段3。拟定3种河段在不同时期河岸土壤性质、河流动力条件和边界条件所对应的指标，如表2所示。

在不同河段河道岸滩安全性综合评价过程中，通过对定性指标和定量指标进行量化处理，得到层次结构模型中底层各影响因子指标的量化值：

式中X1、X2分别为枯水期和洪水期不同河段河道岸滩各影响因子的量化指标矩阵。

表2　3个河段枯水期和洪水期影响指标

3　河道岸滩稳定性综合评价与分析

河道岸滩稳定性综合评价就是通过岸滩稳定性评价层次结构模型和权重系数，利用模糊数学方法将定性指标定量化和定量指标标准化，进而构造枯水期和洪水期岸滩稳定综合评价函数，以评价河道岸滩稳定性。

在确定了岸滩底层各影响指标的量化值后，根据各影响因子指标的权重系数，可以构造河道岸滩稳定综合评价函数，即

式中：G为河道岸滩稳定综合评价指标函数值，G越大，河段稳定性越好；xi为底层各影响因子的标准量化值；wi为底层各影响因子对岸滩安全性作用的权重；n为底层影响因子的数量。

对于枯水期和洪水期的岸滩，已知不同时期各影响因子的权重矩阵W1和W2，以及不同河段影响因子的量化指标矩阵X1和X2，便可求得枯水期和洪水期河段的河道岸滩稳定综合评价函数Gk和Gh，即

利用公式（11）和（12）计算枯水期和洪水期3种河段的河道岸滩稳定综合评价函数值，结果如表3所示。

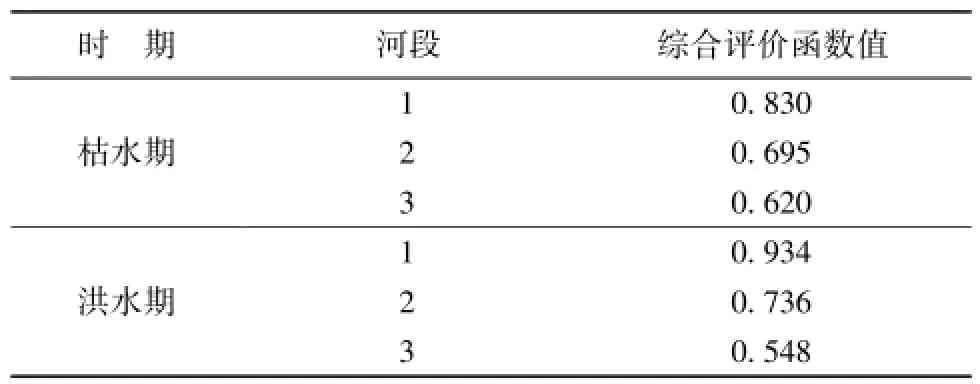
表3　不同河段河道岸滩稳定综合评价函数值

结合表1和表2的实际情况，从表3可以得出：

a.枯水期河段1、河段2和河段3的岸滩稳定综合评价函数值分别为0.830、0.695和0.620，表明河段1最安全，河段2次之，河段3最不安全。3个河段的土壤性质差别较大，河段1土壤性质对应的主要影响因子对岸滩的稳定性最有利，河段3土壤性质对应的影响因子对岸滩稳定性不利，虽然河段1的冲刷较为严重，其岸滩稳定性排序仍为第一位。

b.洪水期河段1、河段2和河段3的岸滩稳定综合评价函数值分别为0.934、0.736和0.548，表明河段1最安全，河段2次之，河段3最不安全。同样，虽然河段1的冲刷、水位变化和河岸浸泡时间都较大，但仍不能超过河岸土壤性质的作用，因此河段1的安全性仍然最好；河段3由于按土壤性质的安全性较弱，再加上水位变化和河岸浸泡时间的影响都较大，使河段3的稳定性最差。

在利用该方法评价河道岸滩稳定性时，需要获得河岸边界条件和河流动力条件中的8个影响因子的指标值。在实际河流中，多数情况没有如此全面的岸滩实测资料，获得诸多实测资料仍有很大的困难。因此，根据河道岸滩边界水流动力特点，本文设计了3种河道岸滩，并拟定了相应影响因子的指标值，目的是介绍河道岸滩稳定性评价的步骤和过程。目前，河道岸滩稳定性综合评价方法还没有针对实际河流岸滩利用实测资料进行的评价和检验，也就是说，该方法若要应用于实际，还有许多工作需要深入研究，这也是我们努力的方向之一。

4　结 语

结合不同时期影响河道岸滩稳定性的主要因素及其差异，利用层次分析法研究了枯水期和洪水期各主要影响因子的作用，根据岸滩稳定性影响因子权重和无量纲化指标的特点，构造了枯水期和洪水期河道岸滩稳定综合评价函数，并对设计的3种不同岸滩河段的稳定性进行了评价。鉴于河道岸滩稳定性综合评价方法还没有应用于实际的河道岸滩稳定性评价，以后还有许多工作需要深入研究。

［1］长江水利委员会.长江中下游护岸工程40年［C］//长江中下游护岸工程论文集（4）.武汉：水利部长江水利委员会，1990：15.

［2］赵业安，周文浩，费祥俊，等.黄河下游河道演变基本规律［M］.郑州：黄河水利出版社，1998.

［3］ABAM T K S.Factors affecting distribution of instability of river banks in the Niger delta［J］.Engineering Geology，1993，35：123-133.

［4］HAGERTY D J，SPOOR M F，ULLRICH C R.Bank failure and erosion on the Ohio River［J］.Engineering Geology，1981，17：141-158.

［5］THOMPSON C，CROKE J，GROVE J，et al.Spatiotemporal changes in river bank mass failures in the LockyerValleyQueensland，Australia［J］. Geomorphology，2013，19（1）：129-141.

［6］中华人民共和国水利部.中国河流泥沙公报2011［M］.北京：中国水利水电出版社，2012.

［7］王延贵.河流岸滩挫落崩塌机理及其分析模式［J］.水利水电科技进展，2013，33（5）：21-25.（WANG Yangui. Study on mechanism and analysis mode of sinking failure for theriverbank［J］.AdvancesinScienceand Technology of Water Resources，2013，33（5）：21-25.（in Chinese））

［8］张芳枝，陈晓平.河流冲刷作用下堤岸稳定性研究进展［J］.水利水电科技进展，2009，29（4）：84-88.（ZHANG Fangzhi，CHEN Xiaoping.Research progress on stability analysis of embankment under effects of river scouring［J］.Advances in Science and Technology of Water Resources，2009，29（4）：84-88.（in Chinese））

［9］王坤.模糊决策理论在崩岸研究中的应用［J］.长江科学院院报，2005，22（8）：12-15.（WANGKun. Application of fuzzy decision-making theory in bank-failure study［J］.Journal of Yangtze River Scientific Research Institute，2005，22（8）：12-15.（in Chinese））

［10］廖小永，王坤.模糊统计聚类理论在崩岸问题中的应用研究［J］.长江科学院院报，2007，24（4）：5-8.（LIAO Xiaoyong，WANG Kun.Study on application of fuzzy statistic clustering theory in bank-failure［J］.Journal of Yangtze River Scientific Research Institute，2007，24（4）：5-8.（in Chinese））

［11］WANG Yangui，JIN Yakun，SHI Hongling.Study on roles of influence factors in river bank failure［C］//Proceedings of35thIAHRWorldCongress.Beijing：Tsinghua University Press，2013：213.

［12］王延贵，金亚昆.模糊层次分析在河道岸滩稳定性评价中的应用［J］.浙江水利科技，2014，42（5）：38-41.（WANG Yangui，JIN Yakun.Application of analytic hierarchy process in evaluation of river bank stability［J］. Zhejiang Hydrotechnics，2014，42（5）：38-41.（in Chinese））

［13］SAATY T L.The analytical hierarchy process［M］.New York：McGraw Hill，1980.

［14］汪浩，马达.层次分析标度评价与新标度方法［J］.系统工程理论与实践，1993（9）：25-26.（WANG Hao，MA Da.Scale evaluation and new scale methods［J］.Systems Engineering-Theory&Practice，1993（9）：25-26.（in Chinese））

［15］张庆华，白玉慧，倪红珍.节水灌溉方式的优化选择［J］.水利学报，2002，33（1）：47-51.（ZHANG Qinghua，BAI Yuhui，NI Hongzhen.Optimal choice of water saving irrigation mode［J］.Journal of Hydraulic Engineering，2002，33（1）：47-51.（in Chinese））

［16］王延贵，匡尚富.河岸崩塌类型与崩塌模式的研究［J］.泥沙研究，2014（1）：13-20.（WANG Yangui，KUANG Shangfu.Study on types and collapse modes of the bank failures［J］.Joural of Sediment Research，2014（1）：13-20.（in Chinese））

Comprehensive evaluation method for river bank stability

WANG Yangui1，QI Meilan2，JIN Yakun2
（1.International Research and Training Center on Erosion and Sedimentation（IRTCES），Beijing 100048，China；2.School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China）

In order to evaluate the influences of the bank boundary condition and the river dynamic condition on bank stability，through quantification of qualitative indices and standardization of quantitative indices，comprehensive evaluation functions for bank stability during the dry period and the flood period were created based on the hierarchical framework model and weight coefficients of the factors of bank failures，and a comprehensive evaluation method for bank stability，considering many factors，was put forward.The results of stability evaluation of three reach banks with different soil properties，bank boundary conditions，and river dynamic conditions show that the comprehensive evaluation function and method are suitable for bank stability evaluation.

river；bank stability；bank failure；analytic hierarchy process；comprehensive evaluation method

TV143+.3

A

10067647（2016）05005505

10.3880/j.issn.10067647.2016.05.010

国家自然科学基金（511792080）；中国水利水电科学研究院科研专项（沙基本科研1438）；“十二五”国家科技支撑计划（2012BAB04B02-2）

王延贵（1963—），男，教授级高级工程师，博士，主要从事水力学及河流动力学研究。E-mail：wangyg@iwhr.com

（20150628 编辑：熊水斌）