GNSS接收机虚拟多频RAIM方法
卢 虎,韩雷晋,谢 岩
(1.空军工程大学信息与导航学院,陕西西安 710077; 2.西北工业大学明德学院,陕西西安 710124)
GNSS接收机虚拟多频RAIM方法
卢 虎1,韩雷晋1,谢 岩2
(1.空军工程大学信息与导航学院,陕西西安 710077; 2.西北工业大学明德学院,陕西西安 710124)
通过对单频接收机的“虚拟多频点”电离层延时关联模型的研究,建立了一种新型单频接收机虚拟多频接收机自主完好性监测方法,给出了虚拟多频故障监测和识别的判据.仿真结果表明,“虚拟多频”接收机自主完好性监测方法不仅突破了传统接收机自主完好性监测算法对可见星数目的限制,而且还能在不改变单频接收机硬件结构的前提下,极大地提升接收机的完好性监测性能,具有很好的理论意义和实用价值.
全球导航卫星系统;接收机自主完好性监测;虚拟频点;奇偶矢量法
导航领域中的“完好性”来源于该领域英文文献中的“Integrity”.美国《联邦无线导航计划(2010 Federal Radionavigation Plan,FRP 2010)》给“完好性”定义为“对导航系统所提供信息正确性的置信度的测量,也包括导航系统在无法用于导航时向用户发出告警的能力”.当前普遍使用的单频接收机自主完好性监测(Receiver Autonomous Integrity Monitoring,RAIM)算法基于当前全球导航卫星系统(Global Navigation Satellite System,GNSS)历元观测量“快照(Snapshot)”,利用原始数据的“自主一致性”检测原理,实现故障检测(Fault Detect,FD)和故障隔离(Fault Identify,FI)两大功能,主要有最小二乘残差法、奇偶矢量法和伪距比较法3种本质等价的实现方法.此类方法在观测到5颗可见星时,可以实现故障检测;观测到6颗可见星时,可以实现故障识别[1-3].其中的奇偶矢量法已被美国航空无线电技术委员会(Radio Technical Commission for Aeronautics,RTCA)推荐为全球导航卫星系统接收机自主完好性监测的基本算法[4].
随着全球导航卫星系统的发展,研究如何有效利用多频信息提升完好性监测能力已成为接收机自主完好性监测领域的研究热点和主流发展方向[5-10].文献[5-6]给出的多频接收机自主完好性监测算法是基于组合导航系统的算法,通过不同系统、不同频点的信息进行完好性监测,但实质仍然为单频完好性算法;文献[7-8]探讨了多系统融合后矢量跟踪环路的接收机自主完好性监测问题,仍沿用单系统接收机自主完好性监测融合的思想;文献[9]基于三频伪距测量误差相互独立的假设,引入了三频融合的接收机自主完好性监测方法,但假设不符合实际情况,存在一定缺陷.而文献[10]基于同一颗卫星不同频点电离层延时与伪距的相关性,在假设不同频点星钟星历误差、对流层延迟和多径等相同情况下,建立了三频接收机自主完好性监测算法,但并未给出多频信息提升接收机自主完好性监测故障检测和故障隔离指标的原因,而且算法引入了不同频点故障的额外判决,算法性能有待提升.
笔者提出的单频接收机可以根据已知频点的电离层延时,推导出接收机“未实际使用”(即所谓“虚拟频点”)的电离层延时模型,并以此为媒介建立起一种新型的单频接收机虚拟多频点接收机自主完好性监测机制.文中给出了所提新方法的详细推导步骤,分析了多频信息提升接收机自主完好性监测故障检测和故障隔离指标的缘由,并用实测数据验证之,结果表明,所提的“虚拟多频”接收机自主完好性监测方法相较于传统多频方法,能在不改变单频接收机硬件结构的前提下,极大地提升接收机的完好性监测性能;且无须进行不同频点间的故障判决处理,极大地降低了算法复杂度,提升了运算的实时性,具有很好的理论意义和实用价值.
1 多频点伪距信息的电离层延时关联模型
设全球导航卫星系统双频接收机对同一颗卫星发射的L1、L2载波信息量测得到的伪距(ρ1,ρ2)观测方程为

已知电离层是一种与电磁波频率有关的弥散性介质,因此不同频点的电离层延时I1、I2不等.但几何距离r、接收机钟差δtu和卫星钟差δt(s)、对流层延时和多径误差T均为公共量,若不考虑伪距测量噪声ερ1、ερ2,则式(1)和式(2)只有等号右边的电离层延时I1、I2不同.
利用电离层延时与载波频率之间的函数关系[11],可计算得到I1与I2的具体数值:

其中,Ne是信号传播路径的电子总数;κ=40.28Ne,为电离层延时参数;f1和f2为载波L1和L2的频率.由式(3)和式(4)可得

即

显然,只要从全球导航卫星系统接收机得到任一频点的电离层延时信息,如I1,即可通过式(6)计算出其他频点的电离层延时.不论是否能够接收到该频点信息,同一卫星不同频点间的伪距残差方程,也即是通过此电离层延时模型建立起关联,是传统多频接收机自主完好性监测方法的理论基础[9-10].
在全球导航卫星系统接收机可以收到多个频点信息时,各频点伪距测量值真实已知,可直接建立关联矩阵[9-10].但是,在无法接收多个频点信息时,也可以基于式(6)“虚拟”出相应虚拟频点的非零伪距,并建立起真实频点和虚拟频点联立的伪距测量量和电离层延时的关联矩阵,同时通过设计算法仅选取真实伪距测量值参与计算.
综上,不论单频接收机是否能够收到其他多个频点的导航信息信号,均可以通过电离层延时模型建立起多个频点间的伪距关联,这就是虚拟频点接收机自主完好性监测方法的理论出发点.
2 虚拟三频接收机自主完好性监测算法
2.1虚拟三频伪距线性观测模型
假定单频全球导航卫星系统接收机当前时刻可观测到n颗可见卫星,拓展式(1)和式(2)为n个卫星的3个频点信号,可得虚拟三频伪距测量量线性化观测方程为

其中,y1元素是真实频点(设为L1频点)n×1维伪距测量值,y2、y3是虚拟出的L2、L5频点的n×1维非零伪距测量值(不妨令y1=y2=y3);H是各频点n×4观测方程的系数矩阵,取值相等;xTF是用户位置改正参数和接收机钟差改正参数等4×1维状态矢量;κ代表n颗卫星的n×1维电离层延时参数;e1、e2和e3表示3个频点上的n×1维去除电离层误差后的测量误差矢量;,为常数,可通过式(5)和式(6)得到,f1、f2和f3是L1(真实)、L2(虚拟)和L5(虚拟)3个导航频点.
式(7)可简写为

其中,yTF是3n×1维伪距量测向量;GTF是3n×(n+4)维用户位置和伪距关联矩阵;TF是(n+4)×1维4维用户位置和n维电离层延时组成的列向量;eTF是3n×1列向量,由多径和接收机噪声协方差及时钟误差和对流层延时的噪声协方差组成.
在文献[10]中,同一颗卫星的不同频点间相互独立的接收机eTF噪声特性被忽略,并被假定相同.但在虚拟三频方法中,另外两个频点的信息完全是虚拟出来的,所以可以认定3路eTF噪声是完全相同的,弥补了传统方法的理论不足.
用奇偶矢量法[1]等传统接收机自主完好性监测算法进行接收机的完好性监测,必须保证测量噪声eTF服从标准正态分布,因此须求得预白化矩阵[10]:


笔者选取最小二乘残差法进行白化处理后的虚拟三频接收机自主完好性监测性能分析.
2.2虚拟三频接收机自主完好性监测算法的奇偶矢量故障检测
虚拟三频观测方程(10)中有3n个方程和(n+4)个未知数,所以生成的奇偶空间维数是(2n-4),构成的奇偶矩阵PTF为(2n-4)×3n矩阵,并满足

采用QR分解或依据虚拟三频仅单频数据真实的特性,简化文献[9]中的分块法得奇偶矩阵PTF:


求得奇偶矩阵PTF后,计算虚拟三频奇偶矢量:

pTF是(2n-4)×1维列向量,取自由度为(2n-4)的χ2分布作为检验统计量.当ESS大于检测门限T时,认为此刻系统存在故障;反之,则视为系统没有发生故障.
由于虚拟三频奇偶矩阵中的P(n-4)×n是经过QR分解得到的,要求可见卫星数必须大于4颗,但同时算法的统计量也服从自由度为(2n-4)的χ2分布.因此,即使只有5颗可见星,也能实现对全球导航卫星系统信号的故障隔离,突破了传统接收机自主完好性监测算法要求6颗以上可见星方能隔离故障卫星的局限,在城市峡谷、电磁干扰环境等许多场景具有很强的实用性.
2.3虚拟三频接收机自主完好性监测算法的故障识别
简明起见,假定单频故障出现在第1颗卫星上,其他位置同理.当真实频点出现故障偏差d后,由式(10)可知

由式(15)可知,当卫星真实频点出现故障时,经过白化处理后,偏差会扩散到虚拟的第2、第3频点上.所以,不能直接利用传统的故障识别方法识别故障卫星.参考单频奇偶矢量法,将奇偶矩阵的3列进行线性组合即可检测故障.
由于虚拟三频奇偶矩阵是(2n-4)×3n矩阵,前n列可以识别第1频点的卫星故障,剩下2n列用于识别两个虚拟频点的卫星故障,显然可以不予考虑.
统计检测量ESS实质上是奇偶矢量模的平方.由于故障的扩散带来了ESS的成倍增大,使得在伪距偏差较小时,也可以得到ESS超过检测门限T.因此,虚拟三频接收机自主完好性监测算法在伪距偏差较小时仍可以进行完好性监测;其次,ESS的扩大使得在每个采样时刻故障检测识别率都比单频接收机自主完好性监测大,可以弥补单频接收机自主完好性监测算法的检测识别率较低问题.
根据偏差d的扩散情况,可以得出以下识别卫星故障的特征偏差矢量:

其中,v1,i是第i颗卫星的第1频点故障识别的(2n-4)×1特征矢量,p1,i是虚拟三频奇偶矩阵第i列,p2,i是虚拟三频奇偶矩阵第(n+i)列,p3,i是虚拟三频奇偶矩阵第(2n+i)列.
由此得到虚拟三频接收机自主完好性监测算法隔离故障星准则:将奇偶矢量pTF向特征偏差线v1,i方向进行投影并作标准化处理,具有最大投影长度的那颗卫星就是故障卫星.
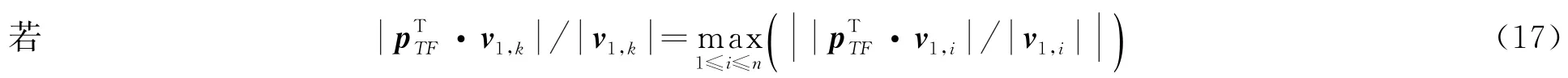
成立,则可以认为第k颗卫星为故障星,必须排除.
3 仿真分析
仿真条件设置:选取全球定位导航系统中的24颗卫星,设置卫星的仰角遮蔽角为7.5°,电离层参数是从全球导航卫星系统接收机(GNRF0302)接收的L1频点中频数据中解算得到的.设三频点分别为f1= 1 575.42 MHz,f2=1 227.60 MHz,f3=1 176.45 MHz,漏警率设为0.001.不失一般性,假定用户接收机以经度116°,纬度40°,高度500 m为初始坐标;运动轨迹为平行赤道轨道向西运动,速度为300 m/s.伪距误差如表1[11]所示.

表1 伪距误差表
为了验证虚拟三频接收机自主完好性监测算法在故障检测与识别方面的性能,并与传统的单频接收机自主完好性监测算法和真实的三频接收机自主完好性监测算法性能进行对比分析,不妨设定第1颗卫星为故障星,并给该颗卫星加上0~200 m的偏差,步长为1 m的偏差.图1给出了故障检测结果的对比图.
从图1可以看出,两种三频接收机自主完好性监测算法对故障卫星进行检测,效果明显优于单频接收机自主完好性监测算法的.单频算法在偏差大于40 m时,检测率才逐渐增大;当偏差达到120 m时,才可以达到100%检测;在偏差小于40 m时,检测率几乎接近于零,检测不出故障卫星.而对于三频和虚拟三频接收机自主完好性监测算法而言,当偏差为10 m时,检测率可达到50%;当偏差高于17 m时,可以100%检测出故障.此外,虚拟三频接收机自主完好性监测算法对卫星的故障检测结果与真实三频接收机自主完好性监测算法几乎相当.

图1 3种接收机自主完好性监测算法故障检测率对比
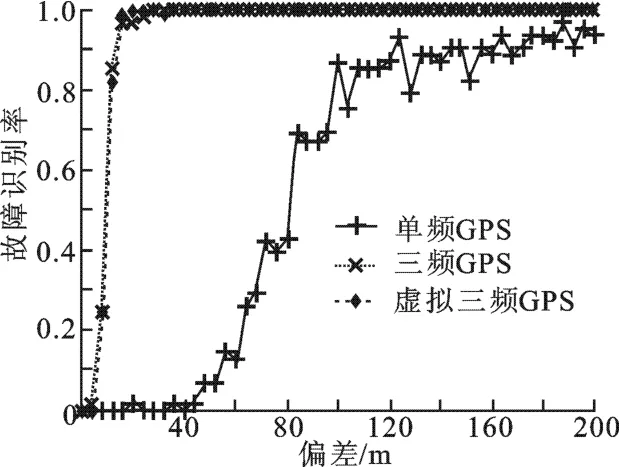
图2 3种接收机自主完好性监测算法故障识别率对比图
考虑到虚拟三频接收机自主完好性监测算法是在不增加多余频点信息的情况下取得此检测结果的,因此优于真实三频接收机自主完好性监测算法.
图2给出了3种接收机自主完好性监测算法对故障卫星的识别图.从图2中可以看出,单频全球定位系统的接收机自主完好性监测算法对故障星的识别效果很差.当偏差增加到200 m时,识别率仍达不到100%,还有故障星在某些时刻不能被识别排除,对接收机定位结果的可靠性没有保证;当偏差较小时,识别效果也不明显;当偏差小于30 m时,识别率为零.而另外两种接收机自主完好性监测算法的效果较好.在偏差达到20 m时,识别率为97%;在偏差高于27 m时,识别率能达到100%.
虚拟三频接收机自主完好性监测算法和真实三频接收机自主完好性监测算法的识别性能都比较好.由于虚拟三频接收机自主完好性监测算法在识别故障星时,不需要进一步识别卫星是哪一频点发生故障,所以计算比较简单.而三频接收机自主完好性监测算法不仅要识别出是哪一颗卫星出现了故障,并且还要识别该故障星的哪一频点出现问题,所以告警时间比虚拟三频接收机自主完好性监测算法的长.此外,在识别出故障星时,虚拟三频接收机自主完好性监测算法直接排除掉故障星即可,但是真实的三频接收机自主完好性监测算法还要进一步分析此刻是排除故障星还是排除故障星中的故障频点.因此,虚拟三频优于真实三频接收机自主完好性监测算法.

图3 单频突发故障检测曲线(偏差40 m)
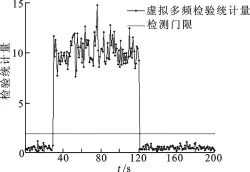
图4 虚拟三频突发故障检测曲线(偏差30 m)
图3给出了采用单频奇偶矢量算法的检测门限与统计检验量的关系图.在30~120 s时对卫星施加故障偏差40 m,会出现统计量在某些时刻已经小于门限值的情形,不能实现100%的检测故障率.
图4给出了采用虚拟三频接收机自主完好性监测算法中检验统计量与检测门限的关系图.在30~120 s时对卫星施加故障偏差30 m,可以看到,由于虚拟三频方法对统计量的扩散带来了ESS的成倍增大,使得在伪距偏差较小时,ESS也远远超过检测门限,从而实现了100%的检测故障率.
4 总 结
通过分析卫星不同频点信号之间电离层延时的相关性,仅利用单一频点的电离层延时I1生成虚拟三频电离层延时矢量,进而给出了虚拟三频接收机自主完好性监测算法.仿真结果表明,该算法不仅突破了传统接收机自主完好性监测方法对可见星数目的限制,同时可以极大地提升接收机的完好性监测性能,具有很好的理论意义和实用价值,有助于促进卫星导航理论的进一步完善与发展.
[1]PARKINSON B W,AXELRAD P.Autonomous GPS Integrity Monitoring Using the Pseudorange Residual[J]. Navigation-Journal of the Institute of Navigation,1988,35(2):255-274.
[2]STURZA M.Navigation System Integrity Monitoring Using Redundant Measurements[J].Navigation-Journal of the Institute of Navigation,1988,35(4):483-501.
[3]王尔申,张淑芳,蔡明,等.遗传粒子滤波的GPS接收机自主完好性监测[J].西安电子科技大学学报,2015,42(1): 136-141. WANG Ershen,ZHANG Shufang,CAI Ming,et al.GPS Receiver Autonomous Integrity Monitoring Algorithm Using the Genetic Particle Filter[J].Journal of Xidian University,2015,42(1):136-141.
[4]YUN H,HAN D,KEE C,et al.RAIM Algorithm Considering Simultaneous Multiple Ramp Failures[J].Aircraft Engineering and Aerospace Technology,2015,87(4):357-367.
[5]卢虎,廉杰.北斗用户机自主完好性监测研究[J].空军工程大学学报,2010,11(3):53-57. LU Hu,LIAN Jie.Research on RAIM Algorithm of Beidou Receiver[J].Journal of Air Force Engineering University,2010,11(3):53-57.
[6]JOERGER M,NEALE J,PERVAN B,et al.Measurement Error Models and Fault-detection Algorithms for Multiconstellation Navigation Systems[C]//2010 IEEE Position Location and Navigation Symposium.Piscataway:IEEE,2010:927-946.
[7]BHATTACHARYYA S,GEBRE-EGZIABHER M.Integrity Monitoring with Vector GNSS Receivers[J].IEEE Transactions on Aerospace and Electronic Systems,2014,50(4):2779-2793.
[8]MUHAMMAD B,CIANCA E,SALONICO A M.Multi GNSS Advanced RAIM:an Availability Analysis[C]//IEEE International Workshop on Metrology for Aerospace.Piscataway:IEEE,2014:28-33.
[9]TSAI Y,CHANG F,YANG W.Using Multi-frequency for GPS Positioning and Receiver Autonomous Integrity Monitoring[C]//Proceedings of 2004 IEEE International Conference on Control Applications.Piscataway:IEEE,2004: 782-786.
[10]郭婧,陆明泉,崔晓伟,等.三频GNSS接收机的RAIM算法研究[J].宇航学报,2011,32(8):1734-1739. GUO Jing,LU Mingquan,CUI Xiaowei,et al.Research on RAIM Algorithm for Triple-frequency GNSS Receiver[J]. Journal of Astronautics,2011,32(8):1734-1739.
[11]谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2011.
(编辑:郭 华)
Novel RAIM algorithm GNSS receiver based on virtual triple-frequency techniques
LU Hu1,HAN Leijin1,XIE Yan2
(1.Information and Navigation Institute,Air Force Engineering Univ.,Xi’an 710077,China; 2.Mingde College,Northwestern Ploytechnical Univ.,Xi’an 710124,China)
In the GNSS era,how to effectively enhance the navigation signal integrity monitoring capacity by using multi-frequency information is becoming a hot topic and the mainstream of RAIM technique.Based on the“virtual”multi-frequency ionospheric delay model of the single-frequency receiver,the paper proposes a novel virtual multi-frequency integrity monitoring technique for the single-frequency receiver,then presents the virtual multi-frequency criterion for fault detection and identification.Simulating results show that the“virtual multi-frequency”RAIM technique not only breaks through the limit to the number of visible satellites of traditional RAIM algorithms,but also greatly enhances the RAIM performance of the receiver without changing the hardware structure of the receiver,which would be of a tempting theoretical and practical value.
global navigation satellite system;receiver autonomous integrity monitoring(RAIM);virtual frequency techniques;parity vector method
TN769.1
A
1001-2400(2016)05-0105-06
10.3969/j.issn.1001-2400.2016.05.019
2015-07-10 网络出版时间:2015-12-10
国家自然科学基金资助项目(61174194,61473308);陕西省自然科学基础研究计划资助项目(2013JM0813)
卢 虎(1975-),男,副教授,博士,E-mail:sdkmsdn@sina.com.
网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151210.1529.038.html

