不确定微观结构复合材料的随机均匀化热性质

尤 芳,陈建军,马 娟,曹鸿钧

(1.西安电子科技大学机电工程学院,陕西西安 710071; 2.西北农林科技大学机电工程学院,陕西杨凌 712100)

不确定微观结构复合材料的随机均匀化热性质

尤 芳1,2,陈建军1,马 娟1,曹鸿钧1

(1.西安电子科技大学机电工程学院,陕西西安 710071; 2.西北农林科技大学机电工程学院,陕西杨凌 712100)

将等效夹杂法和随机因子法相结合,研究了单向纤维三维复合材料有效热特性的随机均匀化分析问题.充分考虑微观结构形态和组成材料特性的随机性及参数之间的相关性,推导了单向纤维增强复合材料随机有效热性质(如热膨胀系数)及其相关性,并与随机因子法和蒙特卡罗法的结果进行了比较.通过对两种方法的结果分析表明,微观结构参数的随机性和相关性对随机均匀化结果具有影响,并得出一些重要结论.

复合材料;均匀化;随机;相关性;有效热性质

非均匀材料可满足传统均匀材料所不能满足的特殊功能要求,在航空航天、汽车、民用建筑等领域得到广泛应用.在材料和力学领域中,基于微观结构几何形状和材料特性知识的均匀化技术作为连接微观尺寸特征与宏观响应的有效方法被广泛用于非均匀材料有效性质的计算.在制造过程中的不确定性将不可避免地影响几何形状和材料参数,材料的不确定性将进一步影响结构的响应.目前,针对非均匀材料在增强相的位置/形状、基体中孔/颗粒等空间分布以及各组成物力学特性具有不确定性的研究越来越多.文献[1]结合等效夹杂法,基于摄动理论估算了形状和体积分数等几何不确定性对均匀化弹性特性概率特征的影响.文献[2]对具有不同纤维纵横比的随机纤维复合材料的弹性特性进行了三维数值模拟.文献[3-6]提出多尺度谱随机方法、扩展有限元法等方法,求解了具有随机细观结构特性或随机形态(如圆盘状或狭缝状随机裂纹)的非均匀材料的有效响应.文献[7]提出一种等效热传导系数均匀化方程数值求解方法,预测单向纤维复合材料以及金属蜂窝夹芯板的等效热传导系数.文献[8]研究了颗粒形状、体积分数和空间分布参数等微结构特征对复合材料有效热传导系数的影响.

迄今为止,现有模型主要考虑微观结构形态或材料特性的随机性.尤其是在均匀化模型中,微观结构参数之间的相关性及随机均匀化结果之间的相关性均未考虑.与微观结构的随机性相比,微观结构参数间的相关性对联系材料整体特性和微观结构特征起着重要作用.此外,诸如纤维增强类的复合材料通常承受热载荷[9],随机均匀化热分析对于估算承受热应力复合结构的可靠性很重要.因此,对不确定微观结构特征及其宏观转变的均匀化进行合理描述将有助于非均匀材料性能预测.

基于上述原因,笔者在充分考虑微观结构不确定性的情况下,将随机因子法(Random Factor Method,RFM)应用于计算单向纤维增强三维复合材料的随机有效热特性,对两相的形态参数和材料特性的不确定性以及上述随机变量之间的相关性做出说明.通过比较随机因子法和蒙特卡罗法(Monte-Carlo Method,MCM)所得到的结果来验证所提方法的有效性.最后,利用蒙特卡罗法获得了宏观有效热特性的相关性.

1　纤维增强复合材料有效热特性的随机均匀化

1.1复合材料均匀化热膨胀系数张量αEI

等效夹杂法作为估算复合材料均匀化弹性性能的有效方法,当利用基于Mori-Tanaka理论的等效夹杂方法估计单向纤维增强复合材料有效热膨胀系数时,其均匀化有效热性能即有效热膨胀系数张量αEI为

其中,αm为基体有效热膨胀系数,Vf是纤维体积分数.矩阵g和φ分别为

其中,I是单位阵,S是材料Elsherby张量,Em、Ef分别是基体及纤维弹性张量,αf是纤维有效热膨胀系数,A=-Vf(S-I),H=(Ef-Em)(S-I)+Ef,β=AH-1,D=I+β(Ef-Em).

对于各向同性材料,其弹性张量E为

其中,e是材料弹性模量,ν是泊松比.

则αEI可表示为

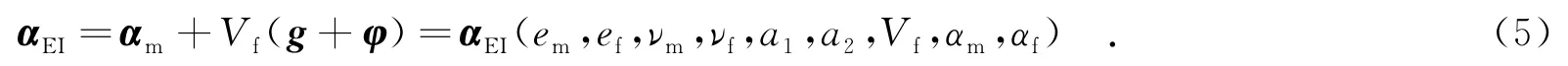
1.2αEI的数字特征

假设基体及纤维的弹性模量em、ef,泊松比νm、νf,有效热膨胀系数αm、αf,纤维横截面尺寸a1、a2,纤维体积分数Vf都具有随机性,同时考虑em和νm、ef和νf、a1和a2之间的相关性.

根据随机因子法[10],随机变量y可表示为随机因子和均值μy的乘积,即y=·μy.可反映y的随机性,并和y服从相同的概率分布.此时,上述随机参数可分别表示为:.其中和分别为相应随机参数的随机因子;和是各随机参数的均值.随机因子的均值为1.0,均方差为和.

当不考虑随机参数之间相关性时,αEI的均方差为

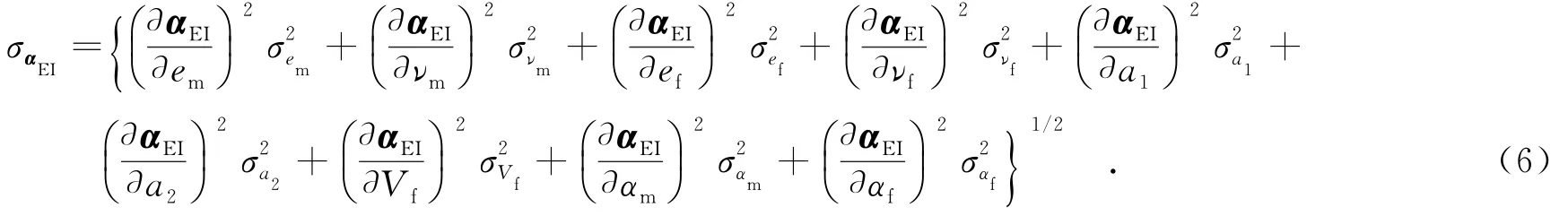
当充分考虑随机参数之间的相关性时,αEI的均方差为

αEI的变异系数为

2　算 例

文中利用基于随机因子法的均匀化分析对单向纤维增强塑料复合材料微观不确定性造成的αEI变化率进行研究.随机微观结构参数(如材料特性、E-玻璃纤维和环氧树脂基体两种组分的热参数以及纤维横截面尺寸)的均值如表1所示.Vf均值设定为0.25,蒙特卡罗法的模拟次数是10000.

表1　纤维和基体的随机参数均值

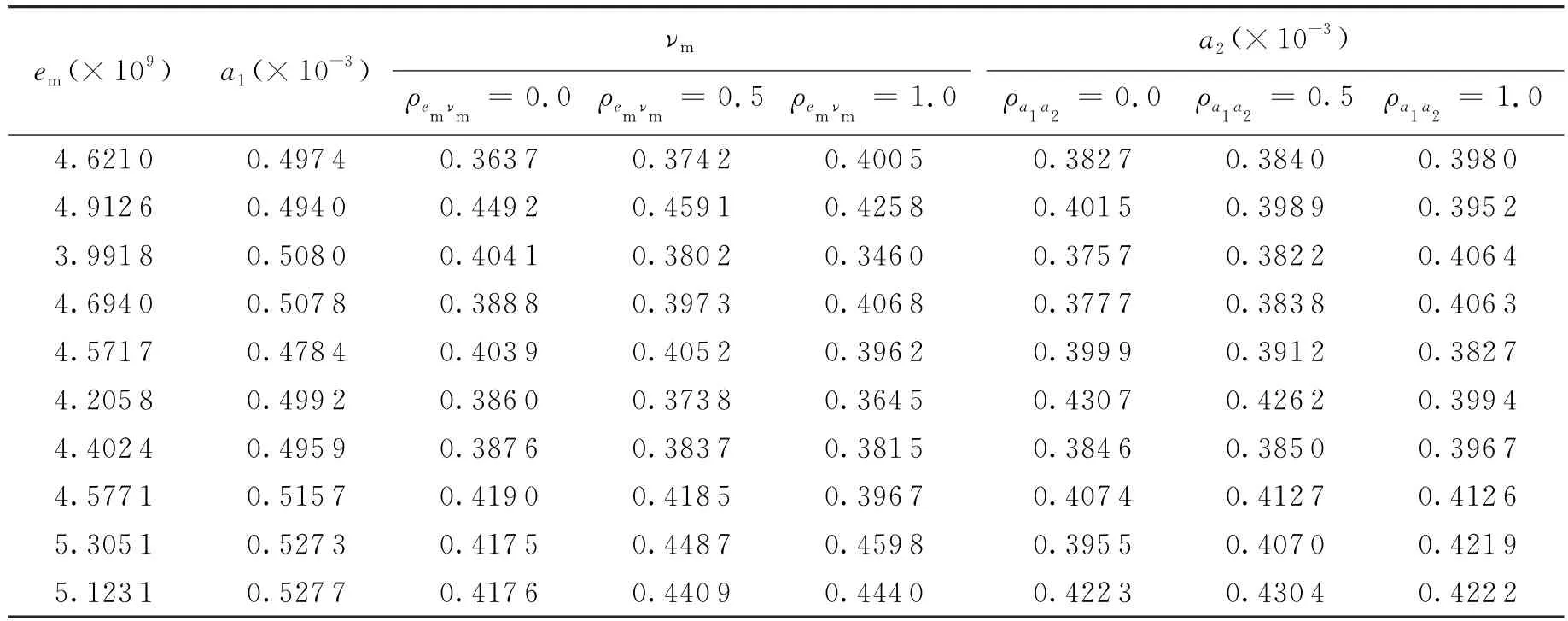
表2　em、νm、a1和a2的10个算例(γem=γνm=γa1=γa2=0.05)

基于随机向量协方差矩阵的丘拉斯基分解,通过蒙特卡罗法得到随机微观结构参数相关性的模拟.根据表1中随机参数em、νm、a1和a2的均值,通过蒙特卡罗法生成服从正态分布和满足不同相关性条件的算例如表2所示.

2.1微观参数随机性对αEI的影响

考虑微观结构参数的随机性,由随机因子法和蒙特卡罗法分别得到αEI的均方差和变异系数,如表3所示.

由表3所示结果可得以下结论:

(1)随机因子法和蒙特卡罗法所得结果相互吻合,从而验证了笔者所提的随机因子法步骤.

(2)各随机参数对αEI随机性具有不同的影响,尤其是对αEI主对角线元素α1、α2和α3影响不同.根据统计结果,αm的随机性对αEI的随机性影响最大;其次是Vf的随机性,主要影响元素α1和α2;再次是νm的随机性,对元素α2产生较大影响;之后是em、ef、a1、a2的随机性,前两个主要影响元素α3,而后两个则对元素α1和α2影响较大;最后是νf和αf的随机性,分别影响元素α2和α3.另外,νf、em、ef、a1和a2的随机性依次对元素α1、α2、α2、α3和α3的随机性没有影响.

2.2微观参数相关性对αEI的影响

同时考虑微观结构参数的随机性及变异系数时,αEI的均方差和变异系数见表4和表5.其中,γ为

表4和表5表明了不同随机参数同时变化时所造成的相互影响.表4和表5中的变异系数远大于表3中的,这表明αEI中每个元素的随机性是所有参数相互作用和相互补充的结果.其次,在同时考虑各参数随机性的情况下,当参数变异系数从0.05变化到0.10时,将增大.此外,考虑所有随机参数相关性所得到的变异系数不同于不考虑或部分考虑相关性所得到的变异系数,再次表明了和对随机均匀化结果相互作用和相互补充的影响.如随或的增大而稍微增大,但当增大时,它几乎保持常量.因此,将随着或或的增大而稍微增大.

表4　不同相关性下αEI的σαEI和(γ=0.05,Vf=0.25)

随机因子法所得结果蒙特卡罗法所得结果ρσα1σα2σα3γα1γα2γα3σα1σα2σα3γα1γα2γα3(×10-5)(×10-5)(×10-5)(×10-2)(×10-2)(×10-2)(×10-5)(×10-5)(×10-5)(×10-2)(×10-2)(×10-2) ρ=0.0 0.558 0.529 0.753 5.079 5.085 4.923 0.558 0.529 0.753 5.078 5.084 4.922 ρ=0.5 0.558 0.529 0.754 5.074 5.082 4.925 0.557 0.529 0.754 5.074 5.082 4.925 ρemνm=0.558 0.529 0.754 5.079 5.085 4.926 0.558 0.529 0.754 5.079 5.085 4.926 0.5 ρefνf=0.558 0.529 0.753 5.079 5.085 4.924 0.558 0.529 0.754 5.079 5.085 4.923 0.5 ρa1a2=0.558 0.529 0.753 5.074 5.082 4.923 0.557 0.529 0.753 5.073 5.081 4.922 0.5

表5　不同随机性和相关条件下αEI的和

表5　不同随机性和相关条件下αEI的和

随机因子法所得结果蒙特卡罗法所得结果γ及ρσα1σα2σα3γα1γα2γα3σα1σα2σα3γα1γα2γα3(×10-5)(×10-5)(×10-5)(×10-2)(×10-2)(×10-2)(×10-5)(×10-5)(×10-5)(×10-2)(×10-2)(×10-2) γ=0.05,ρ=0.0 0.558 0.529 0.753 5.079 5.085 4.923 0.558 0.529 0.753 5.078 5.084 4.922 γ=0.05,ρ=0.8 0.557 0.529 0.754 5.071 5.080 4.927 0.557 0.528 0.754 5.070 5.081 4.927 γ=0.10,ρ=0.0 1.116 1.058 1.506 10.160 10.170 9.845 1.116 1.058 1.507 10.160 10.170 9.845 γ=0.10,ρ=0.8 1.114 1.057 1.508 10.140 10.160 9.854 1.115 1.057 1.508 10.140 10.160 9.854

2.3不同因素对αEI元素间相关性的影响

在充分考虑所有参数的随机性及其相关性的情况下,利用蒙特卡罗法可得αEI各元素间的相关性,如表6所示.

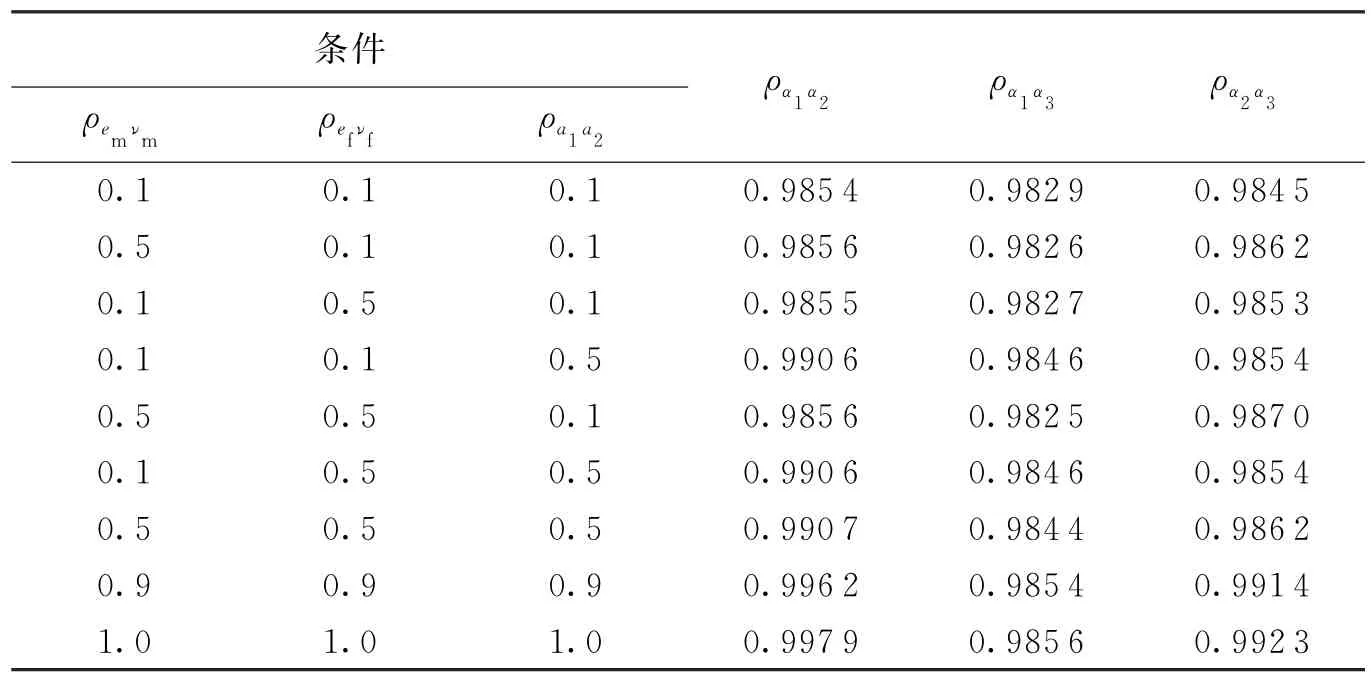
表6　αEI元素间的相关系数(Vf=0.25,γ=0.05)

从表6中可知,无论参数间相关性的强弱如何,元素α1、α2和α3都表现出从0.98变化到1.00的强正相关性.αEI相关性随参数相关性的增大而增大,这表明参数相关性对αEI相关性有正的以及直接的影响.

3　结 论

笔者研究具有微观结构不确定性的纤维增强复合材料的随机均匀化问题,得到微观结构不确定性与宏观热性能之间的关系,推导了均值、均方差和变异系数等数字特征以及有效热膨胀系数张量的相关系数.分别对随机因子法和蒙特卡罗法得到的数值结果进行比较,得出以下结论:

(1)在较低计算成本下,所提方法就可达到与蒙特卡罗法相同的精度;

(2)微观结构参数的随机性及其相关性都会影响随机有效热膨胀系数张量αEI,且不同的随机参数及其相关性对αEI的影响不同;微观结构参数间的相关性不仅影响有效热膨胀系数张量各元素的随机性,而且还影响其取值范围和相关性;αEI的相关性很高,而且随着随机参数相关性的增大而上升.

[1]SAKATA S,ASHIDA F,KOJIMA T.Stochastic Homogenization Analysis on Elastic Properties of Fiber Reinforced Composites Using the Equivalent Inclusion Method and Perturbation Method[J].International Journal of Solids and Structures,2008,45(25):6553-6565.

[2]LU Z X,YUAN Z S,LIU Q.3D Numerical Simulation for the Elastic Properties of Random Fiber Composites with a Wide Range of Fiber Aspect Ratios[J].Computational Materials Science,2014,90:123-129.

[3]TOOTKABONI M,GRAHAM-BRADY L.A Multi-scale Spectral Stochastic Method for Homogenization of Multiphase Periodic Composites with Random Material Properties[J].International Journal for Numerical Methods in Engineering,2010,83(1):59-90.

[4]HIRIYUR B,WAISMAN H,DEODATIS G.Uncertainty Quantification in Homogenization of Heterogeneous Microstructures Modeled by XFEM[J].International Journal for Numerical Methods in Engineering,2011,88(3): 257-278.

[5]VEL S S,GOUPEE A J.Multiscale Thermoelastic Analysis of Random Heterogeneous Materials:Part I:Microstructure Characterization and Homogenization of Material Properties[J].Computational Materials Science,2010,48(1):22-38.

[6]XU X F,STEFANOU G.Explicit bounds on Elastic Moduli of Solids Containing Isotropic Mixture of Cracks and Voids [J].Fatigue&Fracture of Engineering Materials&Structures,2012,35(8):708-717.

[7]张锐,文立华,杨淋雅,等.复合材料热传导系数均匀化计算的实现方法[J].复合材料学报,2014,31(6):1581-1587. ZHANG Rui,WEN Lihua,YANG Linya,et al.Realization Methods of Computational Homogenization for Thermal Conductivity Coefficient of Composites[J].Acta Materiae Compositae Sinica,2014,31(6):1581-1587.

[8]陈云,于艳.颗粒随机分布复合材料的细观构造对有效热传导系数的影响[J].复合材料学报,2012,29(2):145-149. CHEN Yun,YU Yan.Micro-structure of Composites with Randomly Distributed Particles on the Impact of the Effective Thermal Conductivity Parameters[J].Acta Materiae Compositae Sinica,2012,29(2):145-149.

[9]LASCOUP B,PEREZ L,AUTRIAUE L,et al.On the Feasibility of Defect Detection in Composite Material Based on Thermal Periodic Excitation[J].Composites Part B-Engineering,2013,45(1):1023-1030.

[10]尤芳,陈建军,曹鸿钧,等.随机变量下的热传导结构拓扑优化设计[J].西安电子科技大学学报,2014,41(6): 127-134. YOU Fang,CHEN Jianjun,CAO Hongjun,et al.Topology Optimization Design of Heat Conduction Structures with Random Variables[J].Journal of Xidian University,2014,41(6):127-134.

(编辑:郭 华)

Stochastic homogenized thermal properties of composites with an uncertain microstructure

YOU Fang1,2,CHEN Jianjun1,MA Juan1,CAO Hongjun1
(1.School of Mechano-electronic Engineering,Xidian Univ.,Xi’an 710071,China; 2.College of Mechanical&Electronic Engineering,Northwest A&F Univ.,Yangling 712100,China)

Random homogenization analysis of the effective thermal properties of a three-dimensional composite material with unidirectional fibers is presented by combining the equivalent inclusion method with the Random Factor Method(RFM).The randomness of the micro-structural morphology and constituent material properties as well as the correlation among these random parameters are completely accounted for,and stochastic effective thermal properties as thermal expansion coefficients as well as their correlation are then found.Results from the RFM and the Monte-Carlo Method(MCM)are compared.The impact of randomness and correlation of the micro-structural parameters on the random homogenized results is revealed by two methods simultaneously,with some important conclusions obtained.

composites;homogenization;random;correlation;effective thermal properties

TB330.1;O242

A

1001-2400(2016)05-0075-06

10.3969/j.issn.1001-2400.2016.05.014

2015-06-26 网络出版时间:2015-12-10

国家自然科学基金资助项目(51175398,11102143)

尤 芳(1973-),女,讲师,西安电子科技大学博士研究生,E-mail:youfang@nwsuaf.edu.cn.

网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151210.1529.028.html