大规模并行RWG矩量法矩阵填充优化

陈 岩,张 玉,王 永,赵勋旺,林中朝

(西安电子科技大学天线与微波技术重点实验室,陕西西安 710071)

大规模并行RWG矩量法矩阵填充优化

陈 岩,张 玉,王 永,赵勋旺,林中朝

(西安电子科技大学天线与微波技术重点实验室,陕西西安 710071)

针对并行RWG矩量法进程间冗余积分问题,通过优化网格编号提出了一种高效的并行矩阵填充方案.在矩阵块循环分布并行策略基础上,对三角形公共边进行重新编号,使得需要相同三角形积分的矩阵元素分布在同一进程上,从而大幅度地减少进程间的冗余积分计算.数值结果表明,该并行矩阵填充方案消除了绝大部分的进程间冗余积分,提高了并行矩阵填充的效率.

RWG矩量法;并行;矩阵填充方案;优化;冗余积分

作为电磁模拟中最精确的数值方法,矩量法(Method of Moment,Mo M)可以有效地处理各种复杂的电磁问题.但是,矩量法的计算复杂度和内存需求会随着电磁目标电尺寸的增大而急剧增长[1-2].传统的串行RWG(Rao-Wilton-Glisson)矩量法[3]在处理复杂电磁问题时会产生很大的未知量,受计算机单机计算资源的限制,难以有效解决电大尺寸规模的问题.随着当今计算机软硬件的快速发展,利用大规模并行计算技术可以大幅度提高矩量法的计算规模和计算速度,从而高效地完成一系列具有挑战性的大规模电磁工程应用难题[2,4-5].

矩量法处理电磁问题的核心环节是矩阵填充和矩阵方程求解.对于矩阵方程求解,笔者已经有深入的研究[2,4],这里笔者重点关注矩阵的填充过程.RWG矩量法需要将电磁模型剖分成许多三角形面片,并在具有公共边的三角形对上定义RWG基函数.众所周知,在串行RWG矩量法中,利用循环三角形替代循环公共边的方法可以大大减少矩阵填充过程中的冗余积分计算[2],从而提高矩阵填充的效率.在并行RWG矩量法中,对于并发执行的各进程采用这一方案后,各进程内部的冗余积分计算也可以完全消除.然而,并行RWG矩量法在进程之间也引入了大量新的冗余计算,即不同进程之间存在相同的积分计算,这些进程间的冗余计算是无法通过三角形循环消除的.在消除进程间冗余积分方面,鲜有有效工作内容发表,这主要是因为进程间冗余积分涉及到几何建模的过程,使得问题变得异常复杂,而且当并行规模较小时,这一问题并不突出.但是当采用大规模并行计算技术解决实际电磁工程难题时,进程间冗余积分变得十分严重,冗余计算甚至大大地超过有效计算.为此,笔者详细分析了并行RWG矩量法在进程间引入新的冗余计算的原因,并给出了有效的解决方案.该方案在不改变现有矩阵块循环分布并行策略的基础上对算法进行优化,通过对公共边重新编号,尽可能地保证包含相同三角形积分的矩阵元素分布在同一进程上,从而减少进程间的冗余计算,大大地提高了并行矩阵填充效率.

图1　第n个RWG基函数

1　并行RWG矩量法

1.1RWG基函数

图1给出了相邻于第n条公共边的一对三角形T+n和T-n.

RWG基函数的定义式为

其中,ln表示一对相邻三角形的公共边长度,和分别为三角形和的面积.,是从三角形的顶点指向点r的矢量,是从三角形的顶点指向点r的矢量.这种定义方式表明电流是从三角形经过公共边流向三角形.在与三角形对之外,基函数为0.

笔者采用的并行编程模型为消息传递接口(Message Passing Interface,MPI)[6],它是基于分布式内存的并行编程模型,理论上可以扩展到具有任意节点数目的计算平台上.在并行RWG矩量法中,必须首先将矩阵分布到各个进程上.一种有效的数据分布方式就是将大规模稠密矩阵以二维分块循环分布[2,7]的方式分配到所有进程上.假定9×9的矩阵A以2×2的分块大小划分为多个矩阵块,并将其以2×3的进程网格分配到6个进程上,如图2(a)所示,其中小矩形框中的数字代表矩阵元素的索引,图中每一个分块由方框圈出,最外面的虚线表示这些分块未被填满.图2(b)是每个进程上分配的矩阵元素的索引.

图2　二维分块循环分布方案

2　基于网格编号优化的并行填充方案

RWG基函数定义于具有公共边的三角形对上,因此阻抗矩阵元素是按公共边编号索引的.当计算阻抗矩阵元素时,需要在两个三角形对上进行二重面积分.以电场积分方程(Electric Field Integral Equation,EFIE)[8-9]矩量法为例,阻抗矩阵元素Zmn计算过程为

式(2)表明,两个三角形对上的二重面积分可以化为4项.不失一般性,考虑第一项积分,有

图3给出了三角形二重积分与公共边索引关系,图中的小写英文字母表示公共边编号,大写英文字母表示三角形编号.对于第(m,n)个矩阵元素Zmn,首先根据式(2)计算出4组积分IQ、IJ、PQ、PJ;每组积分包含4个积分结果,将这4个积分结果与第m条公共边、第n条公共边以及它们对应的顶点等信息按照一定的运算规则进行运算,然后累加4组计算结果,便可计算出矩阵元素Zmn.

考虑三角形积分PQ,它可用于(m,n)、(m,t)、(m,r)、(k,n)、(k,t)、(k,r)、(l,n)、(l,t)、(l,r)这9个矩阵元素的计算.可见填充矩阵时,若按公共边循环计算阻抗元素,积分PQ最多可能被计算9次,显然这种填充方式引入了大量冗余计算.若按三角形循环来进行相关计算,可首先计算出积分PQ,再将积分值累加到对应的矩阵元素中,这样遍历全部三角形后,便可保证所有矩阵元素都被求出.与按公共边循环的方式相比,按三角形循环来填充矩阵,面积分计算一次可使用9次,有效地避免了冗余积分计算.

图3　三角形二重积分与公共边索引关系

然而,在并行填充方案中,这9个矩阵元素并不一定被分配到同一进程中,这时不同进程都需要计算积分PQ,造成冗余计算.一种有效的解决方案便是想办法让这9个元素被分配到同一进程中.矩阵元素索引直接和公共边编号相关,为了保证这9个矩阵元素被分配到同一进程上,需要对公共边进行重新编号,只要公共边编号变了,对应的矩阵元素索引就会变,矩阵元素分配的进程也会变.只要公共边重新编号得当,便可最大程度地使这9个元素分配到一个进程上,从而避免冗余计算.

综上所述，金属矿山矿下生产作业的核心实质是稳固安全。而电气自动化控制技术能有效地解决相关的安全问题。通过对矿下排水系统、通风系统与运输机械设备的远程自动化控制，可以有效预防与缓解矿下危险事故的发生，为其提高矿业产量与企业壮大发展打下坚持的保障基础

通过以上分析可见,几何上连续(归属于同一个三角形)的公共边对应的矩阵元素不在同一个进程上时,就会导致进程间冗余计算.消除冗余计算的关键需要解决两个问题:哪些公共边是几何上连续的公共边;公共边重新编号对应的新索引应如何获得.

公共边的重新编号必须结合矩阵在进程上的分布方式进行,矩阵是按照二维块循环的方式分布到二维进程网格上的.为消除冗余计算,需使得“几何上连续的公共边”以矩阵元素在进程中的索引顺序进行编号,即公共边重新编号对应的新索引为矩阵元素在进程中的索引.每个矩阵元素有行和列两个方向的索引,因此需要先确定一个方向再对公共边进行重新编号.一般情况下选择行向,因为矩阵方程求解往往要求行向进程数大于列向进程数,这种选择能更好地消除进程间的冗余计算.

不失一般性,假设几何上连续的公共边重新编号之前的索引大致也是连续的.基于这一假设,在实现公共边重新编号时,用新的索引编号直接替换原来连续的索引即可.下面给出一个具体的示例,选择行向索引对公共边重新编号.考虑图2中所示的9×9的矩阵及其分布方式,图4(a)给出了一个与图2相对应的公共边编号示例.

结合图2和图4(a),只关心(5,2)和(5,3)两个矩阵元素,考虑三角形二重积分PQ,可以用于(5,2)和(5,3)的计算,但是(5,2)分配到了进程P00上,而(5,3)分配到了进程P01上,这两个进程都要计算这一积分.为了避免冗余计算,只需要将公共边3的索引变为7即可.这样,三角形二重积分PQ便可以用于矩阵元素(5,2)和(5,7),而这两个矩阵元素都分配在进程P00上.

假设原来在几何上连续的公共边,其编号索引也是连续的,则对这个示例应按照如图4(c)所示的重新编号方案实施.图4(b)中箭头下方的数字,就来源于图2(b)中的行向矩阵索引.公共边重新编号后的结果如图4(c)所示.这种编号方案保证了几何上连续的公共边所对应的矩阵元素能尽可能地分配到同一个进程上.这样的重新编号虽然不能完全消除冗余计算,但可以消除大部分.这在未知量较小的情况下并不明显,但当未知量很大时,冗余计算明显地减少了.

图4　公共边编号优化示例

3　算例仿真

这里以两个飞机模型的散射特性的计算为例,来验证基于公共边重新编号优化的并行矩阵填充方案避免进程间冗余积分计算的有效性.

3.1飞机I的散射特性

此处选取的计算模型为飞机Ⅰ,电磁仿真模型如图5(a)所示.飞机Ⅰ表面为理想导体(Perfect Electric Conductor,PEC),尺寸为11.60 m×7.00 m×2.93 m,计算飞机Ⅰ在500 MHz入射平面波(沿机头方向入射)水平极化情况下的双站雷达散射截面(Radar Cross Section,RCS),相应的电尺寸为1.93λ×1.17λ× 0.49λ.该模型被剖分为25 606个三角形,共有34 824条公共边,故阻抗矩阵大小为34 824×34 824.计算得到飞机Ⅰ的双站RCS结果如图5所示,可见重新编号前后的计算结果吻合良好.

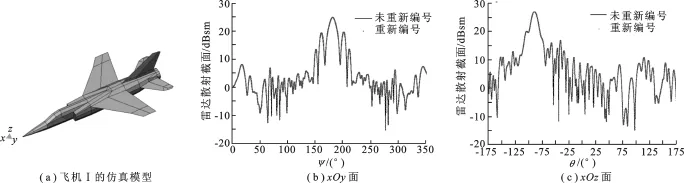
图5　飞机Ⅰ仿真模型及双站雷达散射截面结果

表1给出了公共边编号前后不同进程数、不同进程网格和不同分块大小的情况下,所有进程在矩阵填充过程中的积分次数测试情况.串行算法没有冗余积分,因此称为有效积分.表格中冗余积分次数为所有进程中的总积分次数减去有效积分次数,冗余积分比例为冗余积分次数除以总积分次数.

表1　公共边编号前后矩阵填充过程中的积分次数测试

由表1中编号后的测试结果可见,冗余积分次数可减少约60%,减少程度相当明显.这表明了笔者提出的算法在减少冗余积分计算方面的高效性.

3.2飞机Ⅱ的散射特性

此处选取的计算模型为飞机模型Ⅱ,电磁仿真模型如图6(a)所示.飞机Ⅱ表面为理想导体,尺寸为18.92 m×14.56 m×5.05 m,计算飞机Ⅱ在500 MHz入射平面波(沿机头方向入射)水平极化情况下的双站雷达散射截面,相应的电尺寸为3.07λ×2.43λ×0.84λ.该模型被剖分为125 214个三角形,共有187 821条公共边,故阻抗矩阵大小为187 821×187 821.计算得到飞机Ⅱ的双站雷达散射截面结果如图6所示,可见重新编号前后的计算结果吻合良好.

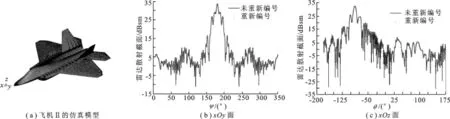
图6　飞机Ⅱ仿真模型及双站雷达散射截面结果

表2给出了公共边重新编号前后的算法在不同进程数、不同进程网格的情况下,所有进程在矩阵填充过程中的积分次数测试情况.表3给出了公共边编号前后矩阵填充时间对比情况.

表2　公共边编号前后矩阵填充过程中的积分次数测试

表3　公共边编号前后矩阵填充时间对比

由表2可见,当并行规模达到数百进程甚至上千进程时,冗余积分比例已经上升到了70%以上.当进程网格为方形时,冗余积分次数减少更为明显,减少约90%,冗余计算几乎被完全消除;当进程网格不为方阵时,冗余积分次数减少率约为66%,减少也很明显,但与进程网格为方阵时相比较差.前面曾指出,对公共边重新编号后,只能保证行向或列向中的一个实现冗余计算降低,除非进程网格为方阵,此时行向和列向的进程数、分块大小都一样,公共边重新编号对两个方向都有效,这一结论在此处得到了验证.

由表3可以看出,填充时间与总积分次数具有一致的下降比例,这说明消除进程间冗余计算所付出的代价极低,公共边重新编号的方案大大提高了并行RWG矩量法矩阵填充效率.

4　总 结

并行RWG矩量法在并行规模增大时,矩阵填充过程中进程间冗余计算迅速增多,使得矩阵填充效率急剧下降.笔者详细分析了并行RWG矩量法在并行矩阵填充过程中进程间存在冗余积分计算的原因,并提出了消除进程间冗余计算的方案.在不改变并行RWG矩量法矩阵块循环分布并行策略的基础上,采用基于网格编号优化的矩阵并行填充方案,使得“几何上连续的公共边”对应的矩阵元素尽可能地分配到同一进程,从而使得需要同一个积分的矩阵元素分布在同一个进程上,大幅度减少了进程间的冗余计算.测试结果也表明了这一方案的有效性.

[1]HARRINGTON R F.Field Computation by Moment Methods[M].New York:IEEE Press Series on Electromagnetic Wave Theory,1993.

[2]ZHANG Y,SARKAR T K.Parallel Solution of Integral Equation Based EM Problems in the Frequency Domain[M]. Hoboken,NJ:Wiley-IEEE Press,2009.

[3]RAO S M,WILTON D R,GLISSON A W.Electromagnetic Scattering by Surfaces of Arbitrary Shape[J].IEEE Transactions on Antennas and Propagation,1982,30(3):409-418.

[4]ZHANG Y,LIN Z C,ZHAO X W,et al.Performance of a Massively Parallel Higher-order Method of Moments Code Using Thousands of CPUs and Its Applications[J].IEEE Transactions on Antennas and Propagation,2014,62(12): 6317-6324.

[5]林中朝,陈岩,张玉,等.国产CPU平台中并行高阶矩量法研究[J].西安电子科技大学学报,2015,42(3):43-47. LIN Zhongchao,CHEN Yan,ZHANG Yu,et al.Study of the Parallel Higher-order Mo M on a Domestically-made CPU Platform[J].Journal of Xidian University,2015,42(3):43-47.

[6]GROPP W,HOEFLER T,THAKUR R,et al.Using Advanced MPI:Modern Features of the Message-passing Interface[M].Cambridge:the MIT Press,2014.

[7]DONGARRA J.Linear Algebra Libraries for High-performance Computers:a Personal Perspective[J].IEEE Parallel and Distributed Technology:Systems and Applications,1993,1(1):17-24.

[8]ECHEVERRI-BAUTISTA M A,FRANCAVILLA M A,VIPIANA F,et al.A Hierarchical Fast Solver for EFIE-Mo M Analysis of Multiscale Structures at Very Low Frequencies[J].IEEE Transactions on Antennas and Propagation,2014,62(3):1523-1528.

[9]YANG K,SHENG W T,ZHU Z Y,et al.Electromagnetic Analysis for Inhomogeneous Interconnect and Packaging Structures Based on Volume-surface Integral Equations[J].IEEE Transactions on Components,Packaging and Manufacturing Technology,2013,3(8):1364-1371.

(编辑:郭 华)

Optimization of matrix filling in the large scale parallel RWG basis based method of moments

CHEN Yan,ZH ANG Yu,WANG Yong,ZHAO Xunwang,LIN Zhongchao
(Science and Technology on Antenna and Microwave Lab.,Xidian Univ.,Xi’an 710071,China)

To solve the issue of inter-process redundant integrals in the parallel Method of Moments (Mo M)using RWG basis functions,an efficient parallel matrix filling scheme is proposed through mesh index optimization.Based on a block-cyclic matrix distribution strategy,the common edges of triangles are renumbered to make the matrix elements that need the same triangular integrals be assigned to one process,thus drastically reducing the inter-process redundant integrals.Numerical results show that the proposed scheme eliminates most of the inter-process redundant integrals and greatly improves the efficiency of parallel matrix filling.

RWG method of moments;parallel;matrix filling scheme;optimization;redundant integral

TN820

A

1001-2400(2016)05-0046-06

10.3969/j.issn.1001-2400.2016.05.009

2015-08-26 网络出版时间:2015-12-10

国家高技术研究发展计划(863计划)资助项目(2012AA01A308);国家自然科学基金资助项目(61301069,61072019);教育部新世纪优秀人才支持计划资助项目(NCET-13-0949);陕西省青年科技新星资助项目(2013KJXX-67);中央高校基本科研业务费专项资金重点资助项目(JY10000902002)

陈 岩(1990-),男,西安电子科技大学博士研究生,E-mail:yuseexidian@163.com.

网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151210.1529.018.html