拟合D-V-A联合谱及各项峰值的人造地震动

盛 涛, 张顺宝,2

(1.宁波大学建筑工程与环境学院 宁波,315211) (2.宁波市住房和城乡建设委员会 宁波,315000)



拟合D-V-A联合谱及各项峰值的人造地震动

盛 涛1, 张顺宝1,2

(1.宁波大学建筑工程与环境学院 宁波,315211) (2.宁波市住房和城乡建设委员会 宁波,315000)

结合D-V-A联合谱的宽频带特点及传统人造地震动方法在拟合各项峰值方面的局限性，提出了一种可同时拟合D-V-A联合谱及各项峰值的人造地震动新方法。根据小波变换的原理，在时-频域将天然地震波加速度时程进行分解，确定对峰值加速度(peak values of acceleration, 简称PGA)和峰值位移(peak values of displacement, 简称PGD)贡献最大的小波分量，对其初步调整后拟合D-V-A联合谱及PGA，PGD值；在此基础上，通过在时域叠加小波函数对加速度时程进行小幅度修正，提高D-V-A联合谱的拟合精度，同时对峰值速度(peak values of velocity,简称PGV)贡献最大的小波分量进行振幅调整，拟合PGV值；循环执行多次后，生成的人造地震动可同时拟合D-V-A联合谱及PGA，PGV和PGD值。算例结果表明，该方法得到的地震动加速度、速度和位移时程不仅对目标反应谱及各项峰值均具有较高的拟合精度，且对天然地震波的改动较小，可用于生成高质量的人工地震波。

D-V-A联合谱； 各项峰值； 小波变换； 人造地震动

引 言

目前，我国的抗震设计规范中仍只考虑地震动的伪加速度反应谱与峰值加速度对结构动力响应的影响。实际上，早在20世纪70～80年代，Housne，Nau等[1-3]已指出，单一的地震动PGA值无法完整地描述地震动的强度特性，峰值速度及峰值位移对中、长周期结构的动力响应将存在更显著的作用。其中：PGV是反应地震动能量特性的主要指标，可间接反应地震动的速度时程对结构的破坏性影响[4-6]；PGD则与结构的位移响应联系最为直接[7-10]，随着基于位移的结构抗震设计理论逐渐完善与成熟[2,9-12]，地震动的PGD也开始引起人们的重视。但迄今为止，我国抗震设计规范中的反应谱法还不能同时考虑地震动的PGV，PGD值对结构动力响应的影响。

相对而言，美国抗震设计规范中的D-V-A联合谱[2]将反应谱周期区间划分为“加速度敏感区”、“速度敏感区”及“位移敏感区”，分别与地震动的PGA，PGV和PGD值相关联，更能反应不同自振频率的建筑结构，在地震动作用下的动力特性，适用于高层建筑结构、基础隔震结构与大跨度桥梁等中、长

周期建筑物的动力性能分析与评估。

为便于按D-V-A联合谱选择建筑结构时程分析用地震动，针对目前已有人工波生成方法的局限性，提出一种新的人造地震动方法，使得生成的人工地震波在拟合D-V-A联合谱的同时，对PGA，PGV和PGD目标值也具有较高的拟合精度，并通过算例进行验证。

1 D-V-A联合谱

由于伪加速度反应谱(SA)、伪速度反应谱(SV)和位移反应谱(SD)存在如下关系

SA/wn=SV=wnSD

(1)

其中：wn=2π/Tn。

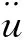
实际上，我国的《核电厂抗震设计规范》中的设计反应谱基本沿用了D-V-A联合谱的思想，但仅适用于基本周期处于4.0 s以下的核电厂工程结构[16]，不能很好地体现地震动位移时程对一般建筑结构动力响应的影响，也难以适用于直接基于位移的抗震设计方法。

2 已有的人造地震动方法及局限性

目前，人造地震动方法主要分为三角级数叠加法及调整天然地震动方法两类。其中，三角级数叠加法因不能真实反应天然地震波的强度及相位非平稳特性，应用受到较大限制[17]。调整天然地震动生成人工波的方法分为时-频域分析方法和时域叠加时程函数法两类。前者主要应用小波变换、HHT变换或S变换等工具[18-23]对地震动的主要时-频分量进行振幅调整以拟合目标反应谱，但是由于各分量的频带难免重叠，其拟合精度一般较低。时域叠加时程函数法则以Hancock等[24]改进的时域叠加小波函数法最为突出，是一种高效的地震动校正方法。该方法在天然地震波的反应谱与设计谱相差较大时，生成的人工地震波对天然地震波的改动很大，收敛性也难以控制。此外，该方法还不能对地面运动的PGV和PGD值进行拟合，其对PGA的拟合也仅仅是通过叠加固定频率特性的正弦或余弦函数予以实现，不符合天然地震动的非平稳特性。

目前部分研究结果已表明[20-21]，将时-频域小波变换方法与时域叠加小波函数法相结合后，应用小波分析方法对天然地震波进行初步调整，不仅可以减小后期应用叠加小波函数法调整时的迭代次数，改善其收敛性，且可使调整后的人工波对天然地震波的改动最小，更符合实际。此外，上述方法还可对特殊工况下的设计反应谱与PGA-PGV或PGA-PGD的目标组合值进行拟合。迄今为止，未见到可以同时拟合D-V-A联合谱与PGA-PGV-PGD目标组合值的相关方法。

为便于按D-V-A联合谱选择时程分析用的天然及人工地震波，用于建筑结构的地震响应分析，有必要发展一种可以同时拟合D-V-A联合谱及PGA-PGV-PGD目标值的人造地震动方法。

3 人造地震动新方法及步骤

天然地震波在应用小波变换分解为多个分量后，每个分量仍具有天然地震波的强度和相位非平稳特性。相对于以往为了在数值上逼近各项峰值，而人为叠加上一些具有固定频率的正弦或余弦函数[24-25]而言，直接应用自身的小波分量进行峰值调整，将更符合实际。因此，笔者提出应用天然地震波的自身小波分量对人工地震波的PGA，PGV和PGD值进行反复修正，并灵活应用小波变换与时域叠加小波函数法提高人工地震波对D-V-A联合谱拟合精度的方法。具体思路和步骤如下：

1) 对天然地震波加速度时程a0(t)应用小波变换进行分解，应用时域积分得到各分量的位移时程。比较a0(t)与各分量的PGA和PGD值及发生时刻，确定影响最大的各小波分量，进行振幅调整后拟合PGA-PGD目标值。

2) 比较a0(t)的反应谱与D-V-A联合谱的区别，对各频段的小波分量进行振幅调整以最大限度拟合D-V-A联合谱。在此基础上，应用时域叠加小波函数法对其作小幅度调整，提高拟合精度(±10%以内)。

经过上述调整后的加速度时程a1(t)能以较高的精度拟合D-V-A联合谱。且由于应用了小波变换调整天然地震波的低频部分(如0.02～0.2 Hz)，不仅解决了时域叠加小波函数法在该区域无法收敛的情况，且实现了对PGD值的拟合。

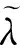
4) 对a2(t)再次应用时域叠加小波函数法拟合D-V-A联合谱。并重复(3)～(4)步直到人工地震波对D-V-A联合谱和PGV的拟合精度均满意为止。此时的人工波记为a3(t)。

实际上，由于第(3)步仅改变了a2(t)中对PGV值影响最大的小波分量，对反应谱值的影响也仅限于该小波分量所处的周期段，因此第(4)步中叠加的时程函数仅起到部分替换该小波分量的作用。

5) 再次确定a3(t)对PGA和PGD值的拟合精度。由于影响各项峰值的小波分量不同，拟合精度的降幅一般不会太大。否则，对贡献最大的小波分量再进行调整，使PGA及PGD再次逼近目标值。

重复以上步骤，直到an(t)对D-V-A联合谱及PGA，PGV和PGD均具有较高拟合精度为止。

4 算例演示与分析

选取1999年台湾集集地震阿里山台站记录到的东西向加速度时程作为范例(以下简记ALS-EW，PGA为0.31g，PGV为67.97 cm/s，PGD为18.34 cm，采样频率为200 Hz)，拟合美国抗震规范中硬土场地条件，PGA为0.31g、PGV为38.69 cm/s、PGD为29.02 cm及阻尼比为5%的弹性D-V-A联合谱[2]。

按照第1)～2)步对ALS-EW记录进行调整，拟合D-V-A联合谱及PGA-PGD后的加速度时程a1(t)如图1所示，速度时程v1(t)和位移时程d1(t)如图2～3所示。其中aPG为PGA值，vPG为PGV值，dPG为PGD值。此时PGA-PGD的精度较高，但PGV的精度较低。

为了提高对PGV的拟合精度，应用小波变换将a1(t)分解9次，此时第10个小波分量的频率区为[0.02, 0.20] Hz。对每个小波分量应用辛普森积分得到其速度及位移时程，其中第7～10个小波分量对PGV及PGD影响最大，分别将其峰值及时刻列于表1-2中。

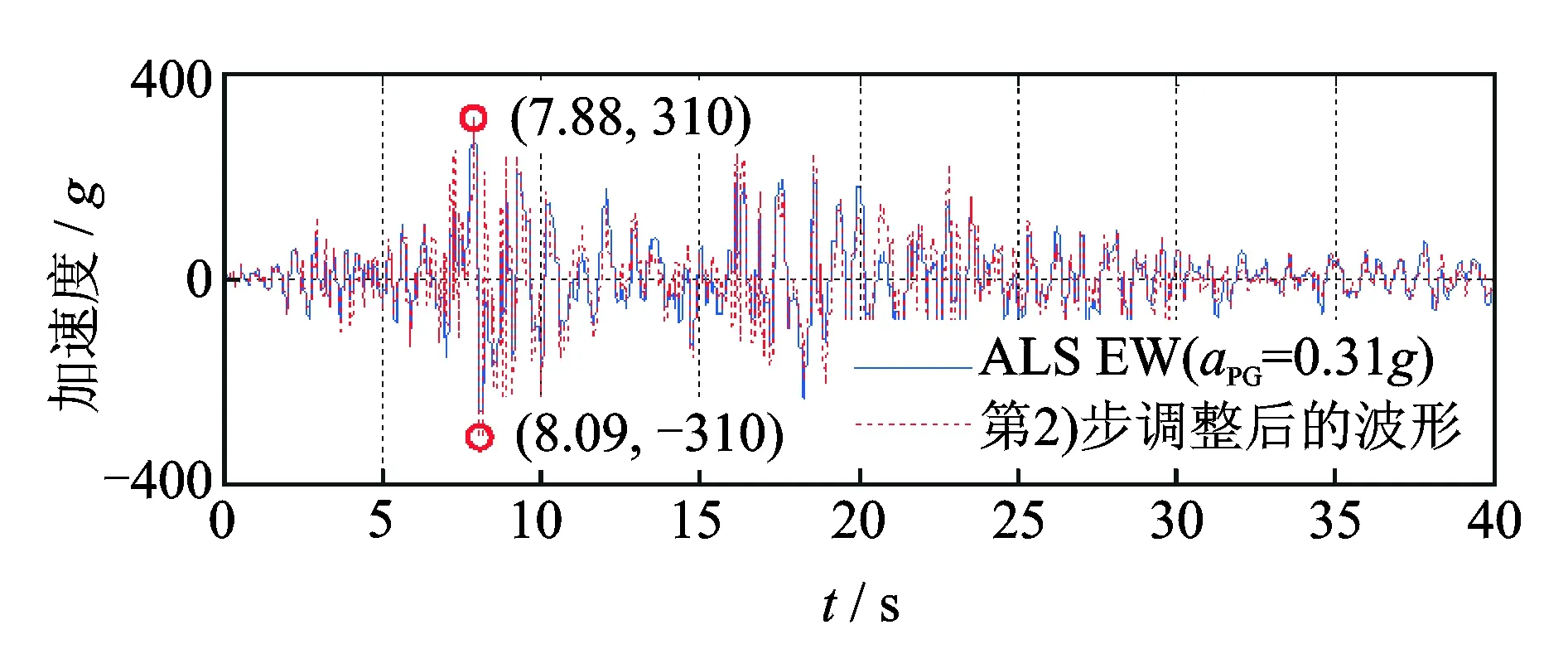
图1 第1)～2)步调整前后的加速度时程Fig.1 Acceleration adjusted by step 1) to 2)

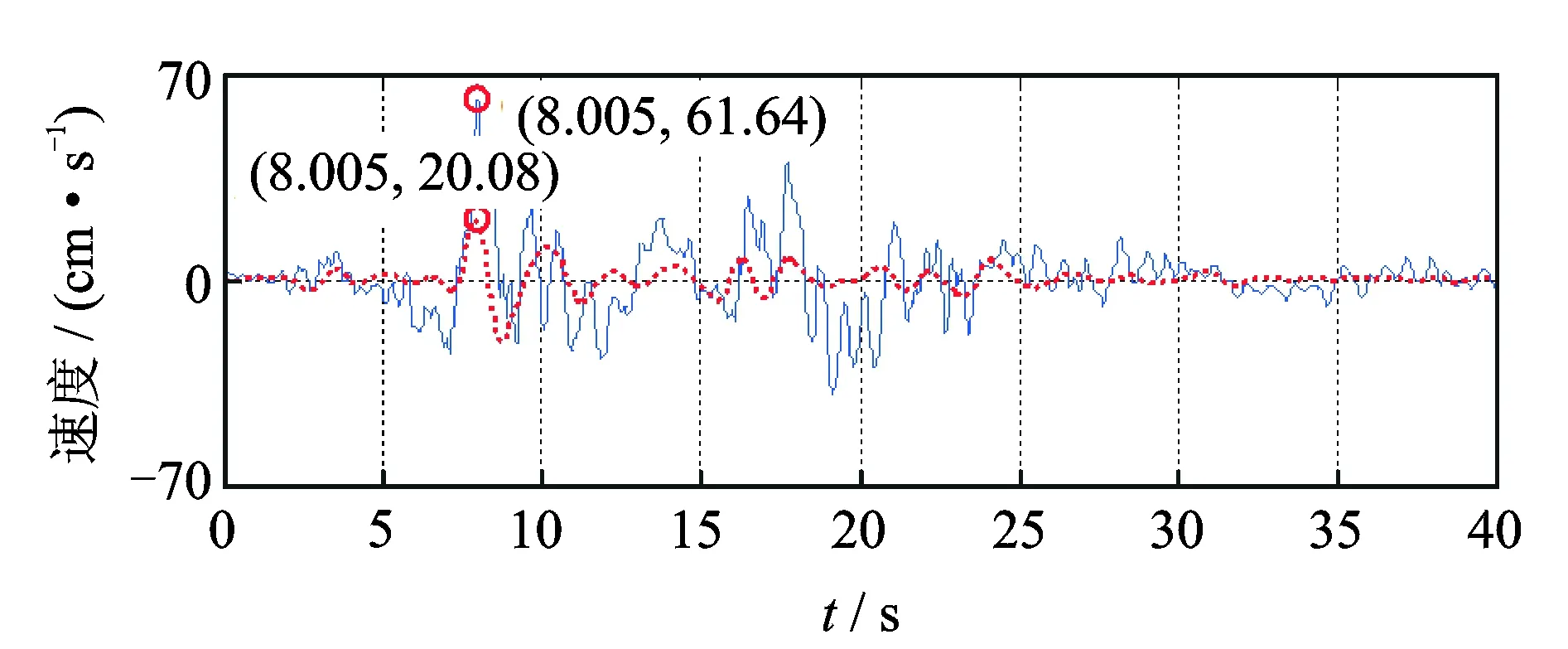
图2 第1)～2)步调整后的速度时程(实线，vPG=61.64 cm/s)及第8个小波分量的速度时程(虚线)Fig.2 Velocity adjusted by step 1 to 2 (solid line, vPG=61.64 cm/s) and the velocity of the 8th wavelet (dotted line)

图3 第1)～2)步调整后的位移时程(实线，dPG=29.46 cm)及第10个小波分量的位移时程(虚线)Fig.3 Displacement adjusted by step 1 to 2 (solid line, dPG=29.46 cm) and the displacement of the 10th wavelet (dotted line)

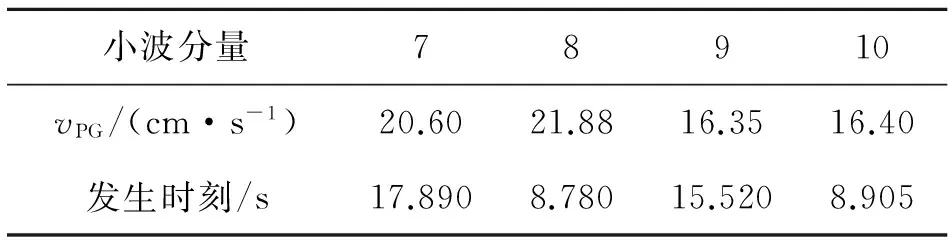
小波分量78910vPG/(cm·s-1)20.6021.8816.3516.40发生时刻/s17.8908.78015.5208.905

表2 各小波分量积分后的PGD值及其发生时刻

与v1(t)的PGV发生时刻8.005 s最为接近的是第8个和第10个小波分量，考虑到第10个小波分量同时对PGD的影响很大，因此仅以第8个小波分量作为调整PGV的主要对象。将其按笔者方法第3)～4)步循环调整4次后，对应的加速度时程a2(t)如图4所示，其速度时程v2(t)的PGV为39.20 cm/s，PGA为0.32g。考虑到图4中的第6个小波分量PGA为0.149g，将该小波分量乘以调整系数λ=-0.01/0.149 =-0.067后叠加到加速度时程a2(t)中，此时PGA为目标值0.31g，PGV则为38.61 cm/s，近似于目标值38.69 cm/s。上述调整步骤对33.0 s以上的反应谱区域未做调整，因此PGD的数值基本不变。

图4 第3)步调整后的加速度时程(实线，aPG=0.32 g)及第6个小波分量的加速度时程(虚线)Fig.4 Acceleration adjusted by step 3 (solid line: aPG=0.32 g) and the 6th wavelet acceleration (dotted line)

最终调整后的人工地震波加速度、速度及位移时程如图5～7所示。与调整前的天然地震波ALS-EW波形相比，由于整个过程是仅对天然地震波的小波分量进行振幅调整，因此人工地震波的加速度、速度及位移时程与天然地震波均较为相似。

图5 天然地震波(实线)与最终调整后的加速度时程(虚线)Fig.5 The natural acceleration (solid line) and the acceleration adjusted finally (dotted line)

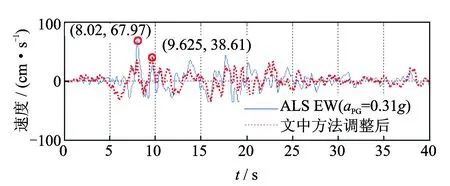
图6 天然地震动(实线)与最终调整后的速度时程(虚线)Fig.6 The natural velocity (solid line) and the velocity adjusted finally (dotted line)

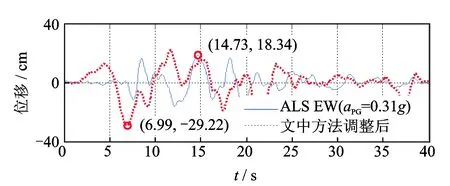
图7 天然地震波(实线)与最终调整后的位移时程(虚线)Fig.7 The natural displacement (solid line) and the displacement adjusted finally (dotted line)

另外，作出天然地震波ALS-EW与人工地震波的D-V-A联合谱如图8所示(图中Ta～Tf为等加速度、等速度和等位移反应谱区段的分界点[2])。由调整结果可知，在上述第(3)～(4)步调整过程中为了拟合PGV目标值，仅对第8个小波分量作了较大改变，对其他小波分量则只是微量的叠加或减除，因此调整后的地震波对D-V-A联合谱仍然具有较高拟合精度。

图8 地震动在调整前后的D-V-A联合谱及目标反应谱Fig.8 The acceleration′s combined D-V-A response spectrum and the target values

综上所述，经过本方法调整后的人工地震波加速度、速度及位移时程在各个频率区间均能很好的满足D-V-A联合谱的统计意义，可全面评估建筑结构的各阶振型对地震响应的影响，是一种高质量的人造地震动。

5 结 论

1) 提出的人造地震动新方法可同时拟合D-V-A联合谱及PGA-PGV-PGD目标组合值，由此生成的人工地震波时程在各个频率区间均能满足D-V-A联合谱的统计意义，有助于实现按D-V-A联合谱选择建筑结构时程分析用的地震动。

2) 应用天然地震波自身的小波分量对其PGA、PGV及PGD值进行调整，能较好地保留天然波的强度及相位非平稳特性。同时结合应用小波变换及时域叠加小波函数法可保证人造地震动对联合谱具有较高的拟合精度。

3) 通过算例演示对本方法的可行性做了验证。结果表明，由该方法生成的人造地震动加速度、速度及位移时程均与原始的天然地震动时程较为相似。当采用其他的天然地震动记录时，可得到多组时频特性不同，但与D-V-A联合谱及各项峰值相兼容的人造地震动时程。

[1] 胡聿贤.地震工程学[M].2版.北京:地震出版社,2006:135-137.

[2] Chopra A K. Dynamics of structures: Theory and applications to Earthquake Engineering[M]. 3rd edition. Englewood Cliffs: Prentice Hall, 2012:222-223,225.

[3] 叶列平,马千里,缪志伟.结构抗震分析用地震动强度指标的研究[J].地震工程与工程振动,2009,29(4):9-22.

Ye Lieping, Ma Qianli, Miao Zhiwei. Study on earthquake intensities for seismic analysis of structure [J]. Journal of Earthquake Engineering and Engineering Vibration, 2009,29(4):9-22. (in Chinese)

[4] Wang Zijun, Zhao Baoming. Correlations between structural damage and ground motion parameters during the Ms8.0 Wenchuan Earthquake[J]. Soil Dynamics and Earthquake Engineering, 2015,72(2):129-137.

[5] Akkar S, Ozen O. Effect of peak ground velocity on deformation demands for SDOF systems[J]. Earthquake Engineering and Structural Dynamics, 2005,34(6):1551-1571.

[6] 郝敏,谢礼立,李伟.从集集地震看建筑物震害与地震动参数的关系[J].地震工程与工程振动,2005,25(6):12-15.

Hao Min, Xie Lili, Li Wei. Study on relationship between building damage and ground motion parameters from Chi-Chi Earthquake[J]. Journal of Earthquake Engineering and Engineering Vibration, 2005,25(6):12-15. (in Chinese)

[7] Bommer J J, Elnashai A S. Displacement spectra for seismic design[J]. Journal of Earthquake Engineering, 1999,3(1):1-32.

[8] 耿方方,丁幼亮,谢辉,等.近断层地震动作用下长周期结构的地震动强度指标[J].东南大学学报:自然科学版,2013,43(1):203-208.

Geng Fangfang, Ding Youliang, Xie Hui, et al. Ground motion intensity indices for long period structures subjected to near-fault ground motion[J]. Journal of Southeast University: Natural Science Edition, 2013,43(1):203-208. (in Chinese)

[9] Michele P, Stefano S, Giada G, et al. A statistical study on the peak ground parameters and amplification factors for an updated design displacement spectrum and a criterion for the selection of recorded ground motions[J]. Engineering Structures, 2014,76(7):163-176.

[10]Faccioli E, Paolucci R, Rey J. Displacement spectra for long periods[J]. Earthquake Spectra, 2004,20(2):347-376.

[11]Medhekar M S, Kennedy D J L. Displacement-based seismic design of buildings: theory[J]. Engineering Structures, 2000,22(3):201-209.

[12]Guan J, Hao H, Lua Y. Generation of probabilistic displacement response spectra for displacement-based design[J]. Soil Dynamics and Earthquake Engineering, 2004,24(2):149-166.

[13]曲哲,叶列平,潘鹏.高层建筑的隔震原理与技术[J].工程抗震与加固改造,2009,31(5):58-63.

Qu Zhe, Ye Lieping, Pan Peng. Theory and techniques of seismic isolation in high-rise buildings[J]. Earthquake Resistant Engineering and Retrofitting, 2009,31(5):58-63. (in Chinese)

[14]方小丹,魏琏,周靖.长周期结构地震反应的特点与反应谱[J].建筑结构学报,2014,35(3):16-23.

Fang Xiaodan, Wei Lian, Zhou Jing. Characteristics of earthquake response for long-period structures and response spectrum[J]. Journal of Building Structures, 2014,35(3):16-23. (in Chinese)

[15]Smerzini C, Galasso C M E, Iervolino I, et al. Ground motion record selection based on broad-band spectral compatibility[J]. Earthquake Spectra, 2014,30(4):1427-1448.

[16]国家技术监督局,中华人民共和国建设部.GB50267-1997,核电厂抗震设计规范[S]. 北京:中国计划出版社,1997.

[17]张郁山,赵凤新.基于小波函数的地震动反应谱拟合方法[J].土木工程学报,2014,47(1):70-81.

Zhang Yushan, Zhao Fengxin. Matching method of ground-motion response spectrum based on the wavelet function [J]. China Civil Engineering Journal, 2014,47(1):70-81. (in Chinese)

[18]曹晖,赖明,白绍良.基于小波变换的地面运动仿真研究[J].土木工程学报,2002,35(4):40-46.

Cao Hui, Lai Ming, Bai Shaoliang. Study on the simulation of earthquake ground motions based on wavelet transform[J]. China Civil Engineering Journal, 2002,35(4):40-46. (in Chinese)

[19]Mukherjee S, Gupta V K．Wavelet-based generation of spectrum-compatible time-histories[J]. Soil Dynamics and Earthquake Engineering, 2002,22(9):799-804.

[20]盛涛,谢异同,袁俊,等.拟合核电厂多维设计反应谱及相关峰值的地震动调整方法[J].振动与冲击,2012,31(18):173-178.

Sheng Tao, Xie Yitong, Yuan Jun, et al. A method of modifying earthquake ground motion for matching multi-dimensional nuclear power plant design response spectra and peak values[J]. Journal of Vibration and Shock, 2012,31(18):173-178. (in Chinese)

[21]盛涛,施卫星,谢异同.拟合多维能量反应谱及峰值速度的地震动调整方法[J].同济大学学报:自然科学版,2012,40(6):807-836.

Sheng Tao, Shi Weixing, Xie Yitong. A modification method of earthquake ground motions for matching multi-dimensional energy input spectra and peak velocity[J]. Journal of Tongji University: Natural Science Edition, 2012,40(6):807-836. (in Chinese)

[22]Ni S, Xie W, Mahesh D P. Generation of spectrum-compatible earthquake ground motions considering intrinsic spectral variability using Hilbert-Huang transform[J]. Structural Safety, 2013,42(5):45-53.

[23]樊剑,吕超,张辉.基于S变换的地震波时频分析及人工调整[J].振动工程学报,2008,21(4):381-386.

Fan Jian, Lü Chao, Zhang Hui. Time-frequency analysis and artificial simulation of earthquake ground motions via S-transform [J]. Journal of Vibration Engineering, 2008,21(4):381-386. (in Chinese)

[24]Hancock J, Watson-Lamprey J, Abrahamson N A, et al. An improved method of matching response spectra of record earthquake ground motion using wavelets[J]. Journal of Earthquake Engineering, 2006,10(1):67-89.

[25]赵凤新,张郁山.拟合峰值速度与目标反应谱的人造地震动[J].地震学报,2006,28(4):429-437.

Zhao Fengxi, Zhang Yushan. Artifical ground motion compatible with specified peak velocity and target spectrum[J]. Acta Seismological Sinica, 2006,28(4):429-437. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2016.05.019

国家自然科学基金资助项目(51408324)；宁波市软科学项目、社发领域科技攻关项目(2014A10089，2014C50067)

2015-02-01；

2015-03-31

TU352.11; P315.3; TH123.1

盛涛，男，1984年9月生，博士、讲师。主要研究方向为地震工程及建筑结构振动控制。曾发表《拟合核电厂设计反应谱及峰值位移的地震动调整方法》(《核动力工程》2012年第33卷第1期)等论文。

E-mail：south_west@126.com