约束层阻尼对薄壁圆柱壳模态参数的影响研究
李晖,张林林,常永乐,闻邦椿
(东北大学机械工程与自动化学院,辽宁沈阳110819)
约束层阻尼对薄壁圆柱壳模态参数的影响研究
李晖,张林林,常永乐,闻邦椿
(东北大学机械工程与自动化学院,辽宁沈阳110819)
以一端约束和一端自由的薄壁圆柱壳为研究对象,研究了约束层阻尼对其模态参数的影响。为了充分了解其振动行为特点,通过有限元法初步获取了其固有频率和模态振型,并搭建了可以准确、高效地测试涂覆约束层阻尼前、后壳体结构模态参数的实验系统,提出了适合该类型阻尼薄壳结构模态参数的测试方法和流程。将约束层阻尼材料制成不同大小的环片形式,并准确获得了涂覆约束层阻尼前、后薄壁圆柱壳的各阶模态参数。基于上述测试结果,研究了约束层阻尼参数的改变对薄壳固有频率、振型和阻尼参数的影响程度,发现约束层阻尼会降低结构的固有频率,但可以有效提升壳体结构的阻尼特性。
振动与波;约束层阻尼;薄壁圆柱壳;模态参数;影响分析;测试方法
0 引言
薄壁圆柱壳由于具有质量轻、承载能力大、适用性好等优点,在实际工程中应用极为广泛。如蒸汽轮机、燃气轮机、航空发动机的转鼓部件,潜艇、鱼雷、导弹的外壳等[1-2]。薄壁圆柱壳模态参数主要包括固有频率、模态振型和阻尼比,有效地获取上述参数是深入研究薄壁圆柱壳振动特性的基础[3],其对于理论建模、响应预估、减振优化设计、振动机理研究等多个环节都具有重要的指导意义。近年来,随着成本的不断降低,制造工艺的不断成熟,约束层阻尼(CLD)越来越受到重视,它们被涂覆到壳体结构表面,通过约束层控制黏性层的剪切变形,将结构振动能量转化为应变能并以热能的形式进行耗散,以达到抑制和减少结构振动的目的。
目前,国内外学者关于涂覆CLD的薄壁圆柱壳的振动特性研究,包括理论建模、分析方法与减振评价等,均已经取得了阶段性的成果。例如,Pan在1969年推导了CLD圆柱壳轴对称振动的6阶偏微分方程[4]。Ramesh等[5]构造了CLD圆柱壳的三角形有限元单元,研究了不同边界条件下黏弹性层剪切模量和结构几何尺寸对结构固有频率和损耗因子的影响。Chen等[6]采用模态假设方法分析了局部涂覆CLD的薄壁圆柱壳的动力学问题,计算结果显示在一定范围内约束层刚度和厚度越大,结构的减振效果越好。但当约束层达到一定厚度时,阻尼效果并非随约束层的增大而增大。Chen等[7]研究了固定大小的带状约束层个数以及长度对圆柱壳阻尼特性的影响,发现带状约束层的长度在一定范围内会显著地增加壳体结构的阻尼,且增大带状约束层的个数有利于提高减振效果,但当其长度超过壳体长度的40%后,减振效果逐步降低。Wang等[8]还采用有限元法对涂覆CLD的圆柱壳进行了研究,仿真结果表明对于大面积涂覆CLD的壳体结构,其减振效果并非总是优于部分涂覆的效果。为了获得较好的阻尼减振效果,必须考虑壳体的材料、几何特性,阻尼层的厚度、位置、覆盖面积以及边界条件的影响。Zheng等[9]等采用数值仿真方法研究了两端简支条件下薄壁圆柱壳的阻尼优化布置问题,研究发现矩形阻尼片的轴向长度相对于圆周宽度比值越大,结构的减振果越明显,且增加涂覆数量也有助于提高减振效果。王淼等[10]采用谱传递矩阵法分析了部分覆盖主动约束层阻尼(ACLD)的圆柱壳振动控制问题,在减少自由度数目和计算工作量方面,收到了一定效果,但他们只限于讨论轴对称模型,研究对象比较简单。李恩奇等[11]采用分布参数传递函数方法对涂覆CLD的圆柱壳进行了分析,获得了系统的固有频率和损耗因子,与传统的解析方法相比,该方法具有更好的几何适应性。向宇等[12]构建了一种新的矩阵方法,并对部分覆盖被动约束层阻尼(PCLD)的圆柱壳进行了高效、高精度振动分析,为采用齐次扩容精细积分法求解PCLD层合圆柱壳的动力学问题奠定了基础。柳承峰等[13]采用渐进结构优化算法,对涂覆CLD的短圆柱壳进行了拓扑优化分析,并计算获得了结构的损耗因子。实验验证结果表明,该种方法能获得满足优化模型的CLD材料拓扑优化布局,工程应用性较强。Jin等[14]提出了一种精确的解析分析方法,获取了弹性边界条件下涂覆CLD的圆柱壳结构的模态参数,并讨论了阻尼层厚度以及剪切参数对固有频率和损耗因子的影响。
但上述研究工作绝大多数局限于理论分析层面,一般采用解析、数值分析方法对涂覆CLD的壳体结构动力学特性进行研究。由此得出的关于阻尼层的厚度、位置、覆盖面积等参数对壳体结构振动特性的影响规律以及减振结论,往往都基于理想的壳体模型和边界条件。而采用试验测试手段,对实际的CLD圆柱壳的振动特性开展试验研究工作的相关文献并不多见。为了满足工程应用的需求,有必要从试验角度深入研究CLD对壳体振动特性的影响程度及规律。
本文以一端约束和一端自由的薄壁圆柱壳为研究对象,研究了CLD对其模态参数的影响。首先,为了充分了解其振动行为特点,通过有限元法初步获取了固有频率和模态振型,搭建了可以准确、高效地测试涂覆CLD前、后壳体结构模态参数的试验系统,并提出了适合获取该类型阻尼薄壳结构模态参数的测试方法和流程。然后,将CLD材料制成不同大小的环片形式,并准确获得了涂覆CLD前、后薄壁圆柱壳的各阶模态参数。最后,基于上述测试结果,研究了CLD参数的改变对壳体结构固有频率、振型和阻尼参数的影响程度。本文的研究可以为客观、准确地评价CLD材料的减振效果提供服务,为创建涂层圆柱壳模型和实施相应的减振优化设计提供试验数据,为推进阻尼减振技术在壳体结构中的全面应用提供技术参考。
1 研究对象及CLD材料
所研究的薄壁圆柱壳其材料为45#钢,弹性模量为2.1×1011Pa,泊松比为0.3,密度为7 850 kg/m3,质量为1 070 g.其长度为95 mm,外半径为144 mm,壁厚为2 mm,它的一端带有安装边,利用一个圆环压板,通过拧紧8个M8螺栓来将其固定到一个刚性、质量很大的方形夹具平台上,方形夹具平台则通过多组螺栓来实现固定。CLD材料为SOUNDFOIL 5D2,其包括有两层,分别为黏弹性层和约束层,其中:黏弹性层厚度为0.13 mm,杨氏模量为12 MPa,泊松比为0.495,密度为1 200 kg/m3;而约束层厚度为0.13 mm,杨氏模量为7×104MPa,泊松比为0.3,密度为2 700 kg/m3.在进行试验时,该类型CLD材料被制成不同大小的环片形式,通过3M无纺布基材双面胶“粘贴”在壳体的不同位置,用以研究约束层涂覆参数的改变对薄壳结构模态参数的影响。
2 基于有限元法的CLD圆柱壳振动特性分析
为了充分了解涂覆CLD薄壁圆柱壳的振动行为特点,有必要通过有限元法对其进行初步的分析。同时,仿真计算获得的固有频率和模态振型结果还有助于在试验中,确定测试频率范围,避免将测点布置在结构的节点或节线上。
本文以涂覆1∶1约束层环片大小的薄壁圆柱壳为例,使用ANSYS软件中的APDL语言进行编程,并采用SHELL181单元建立了薄壁圆柱壳的有限元模型,该模型共包含6 480个节点,960个单元。然后,利用SECDATA命令来定义CLD的厚度及材料参数。最后,利用BlockLanczos方法计算获得了涂覆CLD前、后薄壁圆柱壳的固有频率和模态振型结果,如表1所示。
3 涂覆CLD的薄壁圆柱壳模态参数测试系统和方法
基于第2节有限元方法获得的分析结果,可知涂覆CLD的薄壁圆柱壳,其具有模态密集、局部振动形态复杂等特点。本节针对上述特点,搭建了可以准确、高效地测试涂覆CLD前、后壳体结构模态参数的试验系统,并提出了适合获取涂覆CLD的薄壳结构模态参数的测试方法和流程。
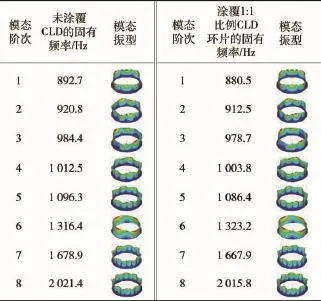
表1 基于有限元法获得的涂覆CLD前、后薄壁圆柱壳的固有频率和模态振型Tab.1 Natural frequencies and modal shapes of thin cylindrical shells with and without CLD obtained by finite element method
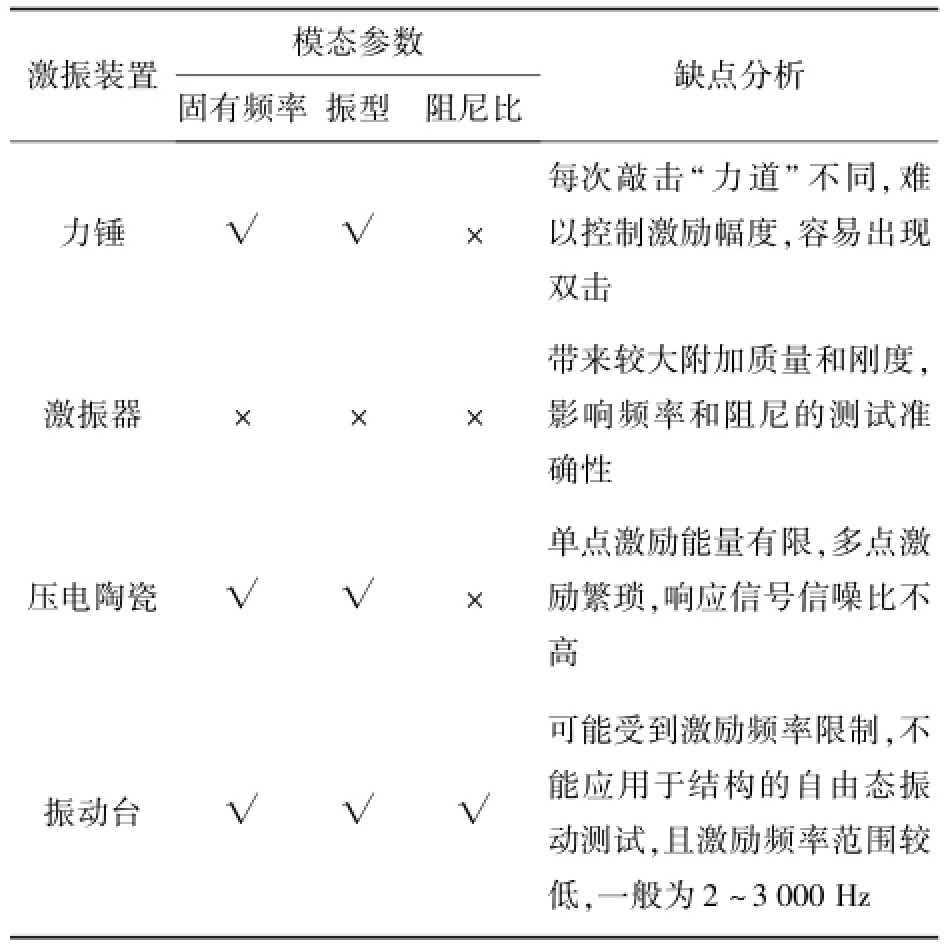
表2 激励薄壁圆柱壳时不同激励方式的缺点分析Tab.2 The weakness analysis of different excitation techniques for thin cylindrical shell
3.1 测试系统
由于薄壁圆柱壳质量轻、壁厚薄,使得传统的加速度传感器不可避免地带来较大的附加质量影响。且由于接触式传感器也会影响薄壳结构的阻尼测量效果,因此本文采用非接触式激光测振仪来获得振动响应信号。另外,根据表2关于各种激振装置缺点的对比分析结果,结合一端约束状态下薄壳结构的振动测试需求,本文最终将可以精确控制激励幅度的振动台选为激振设备,并应用扫频激励方法与分时段快速傅里叶变换(FFT)处理技术来精确获得涂覆CLD前、后壳体结构的固有频率,进而在多点平均测试的基础上,通过半功率带宽法辨识阻尼参数,并通过激光旋转扫描方法获得共振状态下薄壳结构各截面的振动响应数据,经数据处理后可以获得各阶模态振型。图1给出了薄壁圆柱壳模态参数测试系统示意图,实验时共有3个响应测点,分别为测点1、测点2和测点3,其在圆周方向相差120°.使用两组反光镜来灵活地改变激光光路,并使用直流电源为减速电机供电,减速电机则用于驱动反光镜进行定速回转,以实现激光点沿圆柱壳内壁360°圆周扫描。值得注意的是旋转过程中减速电机的振动以及振动台台面的振动可能会影响经由反光镜反射的激光光束的投射效果,并对振型测试造成一定的干扰。因此,有必要采用黏弹性橡胶材料对其进行隔振处理,以确保不会将电机以及振动台台面的振动传递给反光镜装置。

图1 涂覆CLD材料的薄壁圆柱壳模态参数测试系统Fig.1 Test system for modal parameters of thin cylindrical shell with CLD
3.2 测试方法和流程
3.2.1 准确确定薄壳在固支状态对应的拧紧力矩
由于边界状态的改变会对模态测试结果的准确性造成很大的影响,因此必须确保薄壁圆柱壳的模态测试工作是在固支状态下开展的。为此,首先开展预试验,并通过力矩扳手来确定被测壳体夹紧螺栓的最大力矩值。应以统一规定的力矩,并通过力锤快速获得薄壁圆柱壳的前3阶固有频率,至少测试3次,直到各次测试结果相差不大为止(例如3~5 Hz),确定为固支状态所采纳的边界约束条件。若各次测试的频率结果超过10 Hz,则还需重复进行预试验,并进一步增大拧紧力矩,直到获得满意结果为止。
3.3.2 在固支状态下测试获得涂覆CLD前薄壳的各阶模态参数
参照力锤激励获得的固有频率初步值,确定振动台扫频激励的测试频段和扫频速度,并应用分时段FFT处理技术来获得扫频响应信号的频域响应,通过辨识响应峰值来辨识各阶固有频率,进而通过频域带宽法获取各阶阻尼参数。
图2(a)给出了在测试薄壳结构第4阶固有频率和阻尼时,测点1对应的原始响应信号。若直接进行FFT可得到图2(b)所示的频域响应,其响应峰值对应的频率为998.8 Hz.而采用分时段FFT处理技术获得的正确的固有频率结果则是998.1 Hz,如图2(c)所示。如果固有频率出现偏差,则会给阻尼的辨识精度带来很大误差。因此,为了提高测试精度,需要应用分时段FFT处理技术。同时,还需要对测点1、测点2和测点3的数据进行平均处理,以获得最终的频率及阻尼结果。图3给出了3个测点位置获得的用于辨识第3阶固有频率和阻尼时的时域波形和频谱图。另外,为了防止出现模态丢失,在获取其高阶模态参数时,还有必要对更多的测点数据进行测试,以防止部分测点被布置到了结构的节点或节线位置。
最后,使用充足的激励能量激发圆柱壳达到共振状态,并通过激光旋转扫描方法获得共振状态下圆柱壳各截面的振动响应数据,经数据处理后可以获得如图4所示的未涂覆CLD材料时薄壁圆柱壳的前8阶模态振型。
3.2.3 测试获得涂覆CLD后薄壁圆柱壳的各阶模态参数
将CLD材料制成两类不同大小的环片形式:第一类阻尼环片的长宽比分别为1∶1、1∶2、1∶3和1∶6,其中长度为23 mm,每种类型的数量为3个,分别以120°圆周均布的方式粘贴到壳体自由端的外侧位置,如图5(a)所示,用以研究阻尼环片的大小沿壳体圆周方向扩展时对薄壁圆柱壳的各阶模态参数的影响;第二类阻尼环片的长宽比分别为1∶1、1.5∶1、2∶1和3∶1,每种类型的数量也为3个,采用相同的方式布置到壳体结构上,如图5(b)所示,用以研究阻尼环片的大小沿壳体长度方向扩展时对薄壁圆柱壳的各阶模态参数的影响。最后,在与步骤3.2.2相同的测点位置,通过相同的测试方法获得涂覆约束层阻尼后薄壁圆柱壳的各阶模态参数。
3.2.4 分析和总结CLD对薄壳结构模态参数的影响程度及规律
在步骤3.2.3和步骤3.2.4测试获得的涂覆CLD前、后薄壳的各阶模态参数的基础上,将上述数据进行分类、比较和总结。研究CLD参数的改变对壳体结构固有频率、振型和阻尼参数的影响程度及规律。

图2 未涂覆阻尼材料时薄壁圆柱壳的第4阶固有频率Fig.2 The 4th natural frequency of TCS without CLD
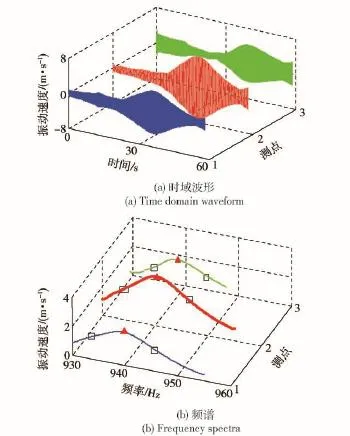
图3 辨识第3阶固有频率和阻尼时的时域波形和频谱图Fig.3 Timedomain waveform and frequency spectra when identifying the 3rd natural frequency and damping at three response points of TCS

图4 未涂覆CLD材料时薄壁圆柱壳的前8阶模态振型Fig.4 The first 8 modal shapes of thin cylindrical shell without CLD
4 CLD圆柱壳模态参数测试结果
根据第3节所提出的涂覆CLD的薄壁圆柱壳模态参数的测试系统、方法和流程,分别将两类CLD环片沿着壳体的圆周方向和长度方向进行涂覆,并依次获取圆柱壳的各阶模态参数。测试时参数设置如下:测量位置为测点1、测点2和测点3,它们位于同一圆周截面,彼此相差120°,该截面距离壳体自由端约为3 mm,测试频率范围0~2 048 Hz,振动台扫频速率1 Hz/s,激励幅度1~4 g,频率分辨率0.125 Hz,响应信号都加汉宁窗处理。
表3、表4分别给出了沿着壳体圆周方向和长度方向改变CLD环片大小时,测试获得的各阶固有频率,并与未涂覆原始状态下的测试结果进行了对比。表5、表6则给出了涂覆CLD前、后壳体结构的阻尼测试结果,并对两种状态下阻尼的变化程度进行了比较。表7还列出了两类阻尼环片大小不同时测试获得的各阶模态振型,其中m和n分别表示轴向波数和周向半波数。

图5 CLD材料沿壳体圆周方向和长度方向大小不同时对应的涂覆形式Fig.5 The different sizes of constrained layers coated along the circumferential and length directions of the shell
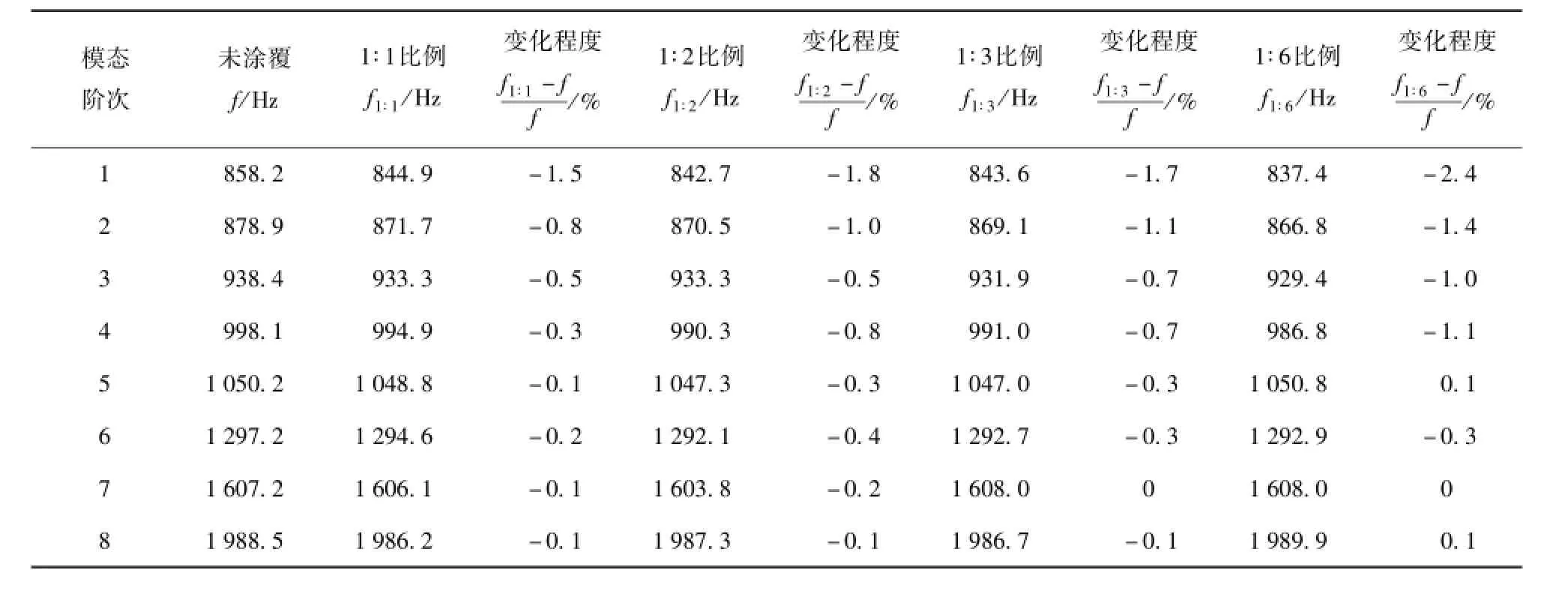
表3 不同CLD环片沿壳体圆周方向的薄壁圆柱壳各阶固有频率Tab.3 The measured natural frequencies of the shells with different sizes of CLD along the circumferential direction
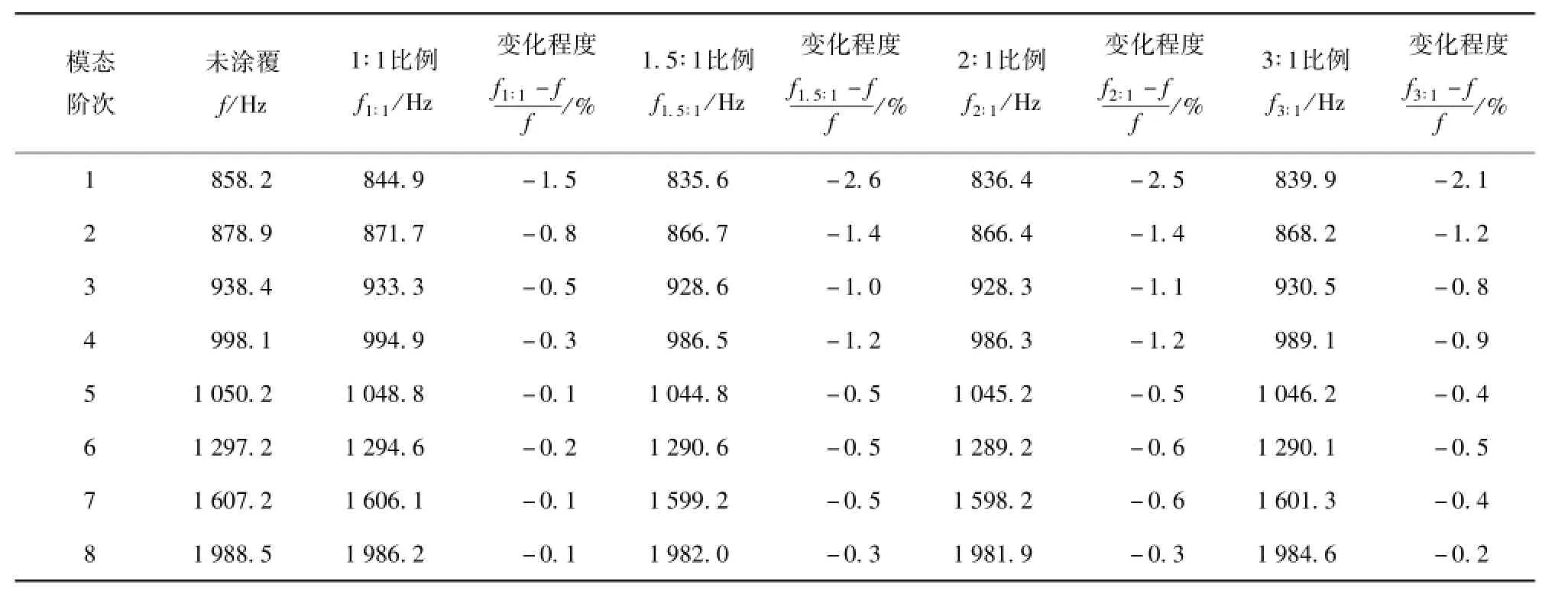
表4 不同CLD环片沿壳体长度方向的薄壁圆柱壳各阶固有频率Tab.4 The measured natural frequencies of thin cylindrical shells with different sizes of CLD along the length direction
5 CLD对薄壁圆柱壳模态参数的影响分析
基于第4节获得的薄壁圆柱壳模态参数测试结果,本节研究了CLD参数的改变对壳体结构固有频率、振型和阻尼参数的影响程度及规律。
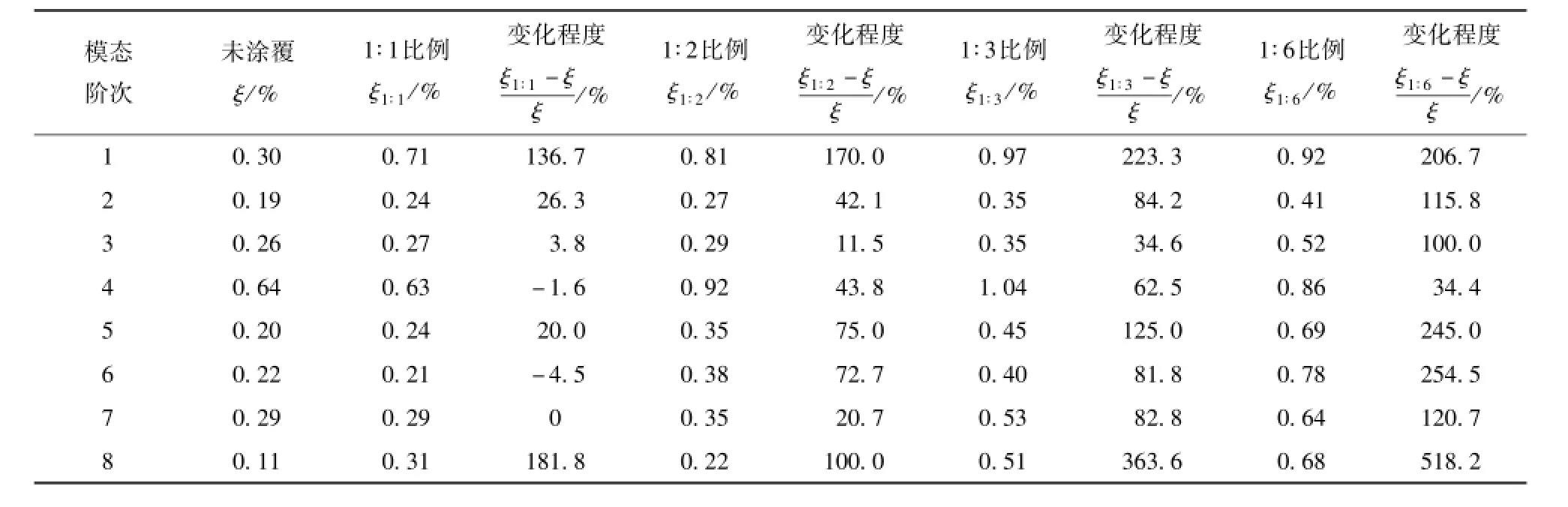
表5 不同CLD环片沿壳体圆周方向的薄壁圆柱壳各阶阻尼比Tab.5 The measured damping ratios of the shells with different sizes of CLD along the circumferential direction
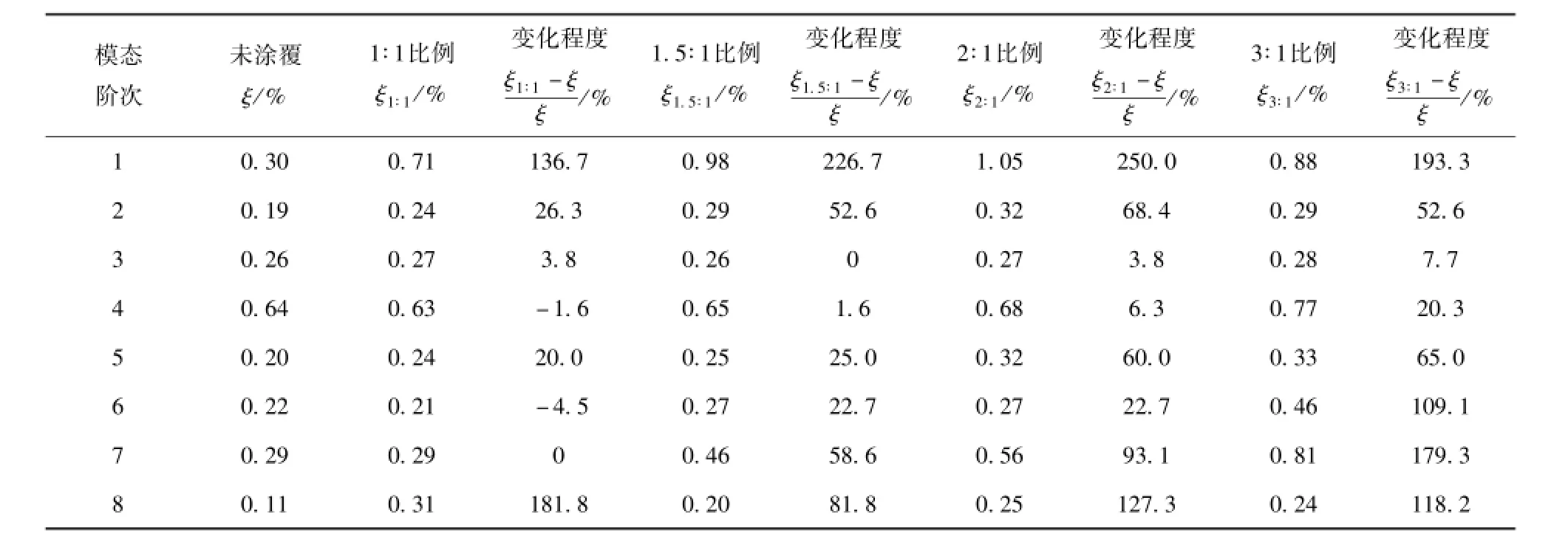
表6 不同CLD环片沿壳体长度方向的薄壁圆柱壳各阶阻尼比Tab.6 The measured damping ratios of thin cylindrical shells with different sizes of CLD along the length direction

表7 不同CLD环片的薄壁圆柱壳各阶模态振型Tab.7 The measured modal shapes of thin cylindrical shells with different sizes of CLD
5.1 CLD对固有频率的影响分析
对表3和表4进行分析可知:1)增加CLD环片的涂覆大小通常会降低壳体结构的固有频率,且结构的低阶固有频率降低程度较为明显,例如第1阶和第2阶,其固有频率降低程度在0.8%~2.6%之间;2)对于高阶固有频率,固有频率降低的程度并不明显,例如第7阶和第8阶模态频率,降低程度只在0.1%~0.6%的范围内;3)沿着壳体圆周方向改变CLD环片大小时,壳体的第1阶和第2阶固有频率降低程度基本与阻尼材料的大小呈正比;但沿着壳体长度方向改变CLD环片大小时,壳体的第1阶和第2阶固有频率降低程度并不是与阻尼材料的大小呈正比,而是在长宽比为1.5∶1时达到最低程度2.6%;4)对比两种沿不同方向改变CLD环片大小的涂覆方式可知,在相同的改变程度下,对于壳体结构的绝大多数模态,沿长度方向改变CLD材料的大小会更大程度地降低该阶次的固有频率值。
5.2 CLD对阻尼参数的影响分析
对表5和表6进行分析可知:1)对于薄壁圆柱壳的绝大多数模态,在其自由端位置增加CLD环片的涂覆大小,会相应地提升该阶次对应的阻尼。特别是阻尼环片大小沿壳体圆周方向达到长宽比1∶6后,阻尼增大效果显著,除了第4阶阻尼外,其他模态阻尼至少增大100%;2)对比两种沿不同方向改变CLD环片大小的涂覆方式可知,两种方式都可以显著地提升结构的第1阶阻尼,且提升程度在170%~250%范围内;3)对比两种方式的阻尼提升效果,沿着壳体圆周方向改变CLD环片大小的方式还可以更为有效地提升结构的高阶模态阻尼,例如第8阶阻尼最大增加了518.2%.
5.3 CLD对薄壁圆柱壳模态振型的影响分析
对表7进行分析可知:改变CLD环片的涂覆大小通常不会导致壳体结构的模态振型出现改变,同未涂覆状态下测试获得的薄壁圆柱壳的振型相同。
6 结论
本文研究了CLD对薄壁圆柱壳模态参数的影响。研究结果表明,改变CLD环片的涂覆大小通常不会导致壳体结构的模态振型出现改变,但会降低壳体结构的固有频率,特别是第1阶和第2阶,其降低程度较为明显。同时,沿着壳体圆周方向涂覆阻尼环片,当其长宽比达到1∶6后,相对于未涂覆状态,CLD圆柱壳的绝大多数模态阻尼显著增大,阻尼增加程度达到100%以上,且该涂覆方式对于提升高阶模态阻尼也有良好效果,例如第8阶阻尼最大增加了518.2%.
(References)
[1] Loy C T,Lam K Y,Shu C.Analysis of cylindrical shells using generalized differential quadrature[J].Shock and Vibration, 1997,4(3):193-198.
[2] Farshidianfar A,Farshidianfar M H,Crocker M J,et al.Vibration analysis of long cylindrical shells using acoustical excitation[J].Journal of Sound and Vibration,2011,330(14):3381-3399.
[3] Ewins D J.Modal testing:theory and practice[M].Latchworth: Research Studies Press,1984.
[4] Pan H H.Axisymmetrical vibrations of a circular sandwich shell with a viscoelastic core layer[J].Journal of Sound and Vibration,1969,9(2):338-348.
[5] Ramesh T C,Ganesan N.Finite element analysis of cylindrical shells with a constrained viscoelastic layer[J].Journal of Sound and Vibration,1994,172(3):359-370.
[6] Chen L H,Huang S C.Vibrations of a cylindrical shell with partially constrained layer damping(CLD)treatment[J].International Journal of Mechanical Sciences,1999,41(12):1485-1498.
[7] Chen L H,Huang S C.Vibration attenuation of a cylindrical shell with constrained layer damping strips treatment[J].Computers and Structures,2001,79(14):1355-1362.
[8] Wang H J,Chen L W.Finite element dynamic analysis of orthotropic cylindrical shells with a constrained damping layer[J].Finite Elements in Analysis and Design,2004,40(7):737-755.
[9] Zheng H,Cai C,Pau G S H,et al.Minimizing vibration response of cylindrical shells through layout optimization of passive constrained layer damping treatments[J].Journal of Sound and Vibration,2005,279(3):739-756.
[10] 王淼,方之楚.主动约束层阻尼部分覆盖圆柱壳耦合振动控制[J].应用力学学报,2005,22(4):545-549. WANG Miao,FANG Zhi-chu.Coupled vibration control of cylindrical shells partially treated with active constrained layer damping[J].Chinese Journal of Applied Mechanics,2005,22(4): 545-549.(in Chinese)
[11] 李恩奇,李道奎,唐国金,等.约束层阻尼圆柱壳动力学分析[J].工程力学,2008,25(5):6-11. LI En-qi,LI Dao-kui,TANG Guo-jin,et al.Dynamic analysis of constrained layer damping cylindrical shell[J].Engineering Mechanics,2008,25(5):6-11.(in Chinese)
[12] 向宇,黄玉盈,陆静,等.部分覆盖PCLD圆柱壳振动分析的新矩阵方法[J].振动工程学报,2009,22(2):175-182. XIANG Yu,HUANG Yu-ying,LU Jing,et al.A matrix method for analyzing vibration of a circular cylindrical shell with partially constrained layer damping treatment[J].Journal of Vibration Engineering,2009,22(2):175-182.(in Chinese)
[13] 柳承峰,李以农,郑玲,等.约束层阻尼短圆柱壳拓扑优化分析及实验研究[J].振动与冲击,2013,32(18):49-53. LIU Cheng-feng,LI Yi-nong,ZHENG Ling,et al.Topology optimization and tests for a short cylindrical shell with constrained layer damping[J].Journal of Vibration and Shock,2013,32(18):49-53.(in Chinese)
[14] Jin G,Yang C,Liu Z,et al.A unified method for the vibration and damping analysis of constrained layer damping cylindrical shells with arbitrary boundary conditions[J].Composite Structures,2015,130:124-142.
The Influence of Constrained Layer Damping on Modal Parameters of Thin Cylindrical Shell
LI Hui,ZHANG Lin-lin,CHANG Yong-le,WEN Bang-chun
(School of Mechanical Engineering and Automation,Northeastern University,Shenyang 110819,Liaoning,China)
The influence of constrained layer damping(CLD)on the modal parameters of thin cylindrical shell(TCS)is investigated.In order to fully understand the vibration characteristics of TCS,the natural frequencies and modal shapes of TCS are roughly obtained by finite element method.An experiment system is established to measure the modal parameters of the shell with constrained layer with high accuracy and efficiency,and the corresponding test methods and procedures which are suitable for measuring the modal parameters of the shell with or without constrained layer are also proposed.CLD material is made into the annular slices with different sizes,and the modal parameters of TCS with or without constrained layer are accurately obtained.Based on the measured results,the influences of varied dimensional parameters of such constrained layer on natural frequency,mode shape and damping of the shell structure are analyzed in details.It is discovered that CLD may reduce the natural frequency of TCS,but it can effectively improve its damping characteristics.
vibration and wave;constrained layer damping;thin cylindrical shell;modal parameter;influence analysis;test method
TB53
A
1000-1093(2016)07-1337-08
10.3969/j.issn.1000-1093.2016.07.024
2016-01-06
国家自然科学基金项目(51505070);中央高校基本科研业务费专项资金项目(N150304011);国家重大科学仪器设备开发专项项目(2013YQ470765)
李晖(1982—),男,讲师。E-mail:lh200300206@163.com

