A quasi-one-dimensional model for hypersonic reactive flow along the stagnation streamline
Chen Song,Sun Qunhu,b,*
aState Key Laboratory of High Temperature Gas Dynamics,Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China
bSchool of Engineering Science,University of Chinese Academy of Sciences,Beijing 100049,China
A quasi-one-dimensional model for hypersonic reactive flow along the stagnation streamline
Chen Songa,Sun Quanhuaa,b,*
aState Key Laboratory of High Temperature Gas Dynamics,Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China
bSchool of Engineering Science,University of Chinese Academy of Sciences,Beijing 100049,China
This study proposes a quasi-one-dimensional model to predict the chemical nonequilibrium flow along the stagnation streamline of hypersonic flow past a blunt body.The model solves reduced equations along the stagnation streamline and predicts nearly identical results as the numerical solution of the full-field Navier-Stokes equations.The high efficiency of this model makes it useful to investigate the overall quantitative behavior of related physical-chemical phenomena.In this paper two important properties of hypersonic flow,shock stand-off distance and oxygen dissociation,are studied using the quasi-one-dimensional model with the ideal dissociating gas model.It is found that the shock stand-off distance is affected by both chemical and thermal non-equilibrium.The shock stand-off distance will increase when the flow conditions are changed from equilibrium to non-equilibrium,because the average density of the shock-compressed gas will decrease as a result of the increase in translational energy.For oxygen dissociation,the maximum value of its dissociation degree along the stagnation line varies with the flight altitude.It is increased at first and decreased thereafter with the altitude,which is due to the combination effect of the equilibrium shift and chemical non-equilibrium relaxation.The overall variation of the maximum dissociation is then plotted in the speed and altitude coordinates as a reference for engineering application.
1.Introduction
It is well known that a vehicle traveling at hypersonic speed will excite the air to a high temperature and change its thermochemical properties.For instance,Hansen and Heims1made an earlier review of the thermodynamic,transport and chemical reaction rate properties of high temperature air and summarized the air chemistry near stagnation region in the coordinate system of speed and altitude.Gupta et al.2presented a later review for an 11-species air model and added lines in the plot to specify the non-equilibrium regions,which is a very rough estimation since the previous equilibrium air chemistry was still adopted.The detailed aerothermodynamics,however,has not been fully recognized although great efforts have been done since then.There are still more unsolved problems than solved problems in hypersonic aerothermodynamics according to Park3in a recent review article.Among twelve unsolved problems,nine problems are related to thermochemical non-equilibrium processes.Park suggested to improve non-equilibrium models and to study thermochemical phenomena for gas mixtures other than air in the future.
If non-equilibrium models are prescribed for the surrounding flow during hypersonic flight,there should be no significant technical difficulties for latest computational fluid dynamics(CFD)to simulate.Model complexity and mesh resolution4,however,would make CFD simulations time-consuming,which is not suitable for parameter studies on thermochemical models or for a fast analysis over a wide range offlow conditions.Theoretical or semi-theoretical approaches,on the other hand,may enable to recognize the influence of the main physical parameters of a specific flow situation by focusing only on part of the entire flow field.Thus simplified simulation would be an alternative means to study hypersonic flow under specific conditions.
The earliest theoretical work on non-equilibrium chemistry for hypersonic flow is probably the one presented by Freeman5who adopted the ideal dissociating gas model of Lighthill6and assumed that the pressure,enthalpy and velocity were constant along streamlines.A set of ordinary differential equations were then obtained and employed to study the behavior offlow through a normal shock wave and flow behind the bow shock wave of a sphere.A number of other methods were developed thereafter including the inverse method by Lick7,the method of integral relaxation by Belotserkovskii and Dushin8,and the time-dependent technique by Kyriss.9These approaches utilize the integral properties of the conservation equations that are simplified in a suitable manner.For instance,the inverse method requires the shape of the detached shock be prescribed for flow over a blunt body,and then the postshock flow field can be advanced using the method of characteristics.This kind of approach is useful to estimate the whole or a large part of the overall flow field,although their accuracy and efficiency are not as good as the latest CFD techniques.
Later theoretical studies on non-equilibrium chemistry mainly focus on the shock stand-off distance that it is an important parameter characterizing the blunt body flow in the stagnation region.Hornung10found that the shock stand-off distance depends on a dimensionless dissociation rate immediately behind the normal shock.According to this concept,Wen and Hornung11proposed an approximate theory in which the shock stand-off distance depends on a modified reaction rate parameter and the density ratio between shock and body.Another approach suggested by Olivier12is based on the solution of the simplified governing conservation equations.It is a quasi-one-dimensional model and is very easy to be solved numerically.Belouaggadia et al.13removed some restrictions of Olivier’s method and constructed a more complex model to describe the chemical non-equilibrium flow along stagnation streamline.The shock stand-off distance predicted by the model of Belouaggadia et al.is shown to be very close to Wen and Hornung’s results,although the post-shock pressure is assumed constant and the contribution of the static enthalpy to the total enthalpy is neglected.
In this study,we aim to develop a quasi-one-dimensional model to predict the flow along the stagnation line,which is not limited to the shock stand-off distance.The model solves a set of partial differential equations derived from the full Navier-Stokes equations.Compared to previous literature studies including our earlier work in the theoretical modeling of blunt body flow14,the present model only assumes that the mass flux is linearly distributed along the stagnation line in the region between shock and stagnation point,which is verified using the full field solution of the Navier-Stokes equations.The model is detailed in Section 2 and validated in Section 3.A couple of applications are analyzed in Section 4,which studies the shock stand-off distance and dissociation of oxygen during hypersonic flight.Section 5 gives some concluding remarks that end this work.
2.Quasi-one-dimensional model
The typical flow pattern of blunt-body flow is shown in Fig.1,which is characterized by a three-layer structure,i.e.,free stream,post-shock inviscid region and boundary layer.In Fig.1,U∞is the free stream velocity,Rnis the nose radius of the body,and Δ and δ are the shock stand-off distance and boundary layer thickness,respectively.The boundary layer of a hypersonic flow is usually very thin,and then the flow can be treated as inviscid to a very good approximation if surface properties are less interested.In this paper,we firstly illustrate the quasi-one-dimensional model under viscous conditions using the spherical coordinate system(r,θ,φ).Then,the model is solved for applications under the inviscid approximation and ideal dissociation gas assumption.
2.1.Flow description
The Navier-Stokes equations are valid for hypersonic flows when the rarefied effects are negligible.In the vicinity of the stagnation streamline,the problem is spherical-symmetric and the governing equations are simplified in the spherical coordinate(r,θ,φ)as follows.
Continuity equation:
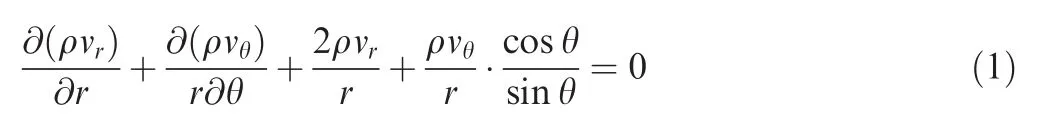
where ρ is the density,vrand vθare the velocity components in the r and θ directions,respectively.
Momentum equations:
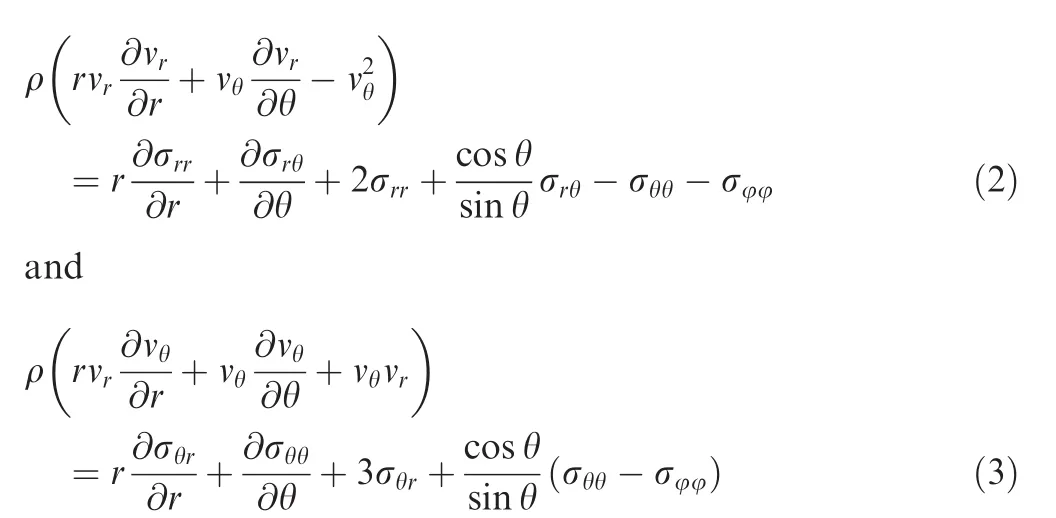
where σijis the ijth component of the stress tenor.
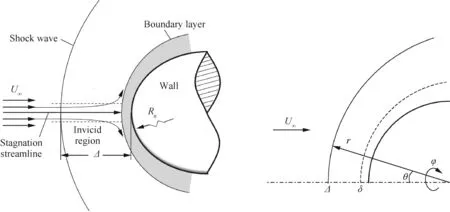
Fig.1 Schematic diagram of hypersonic flow over a blunt body.
Energy equation:
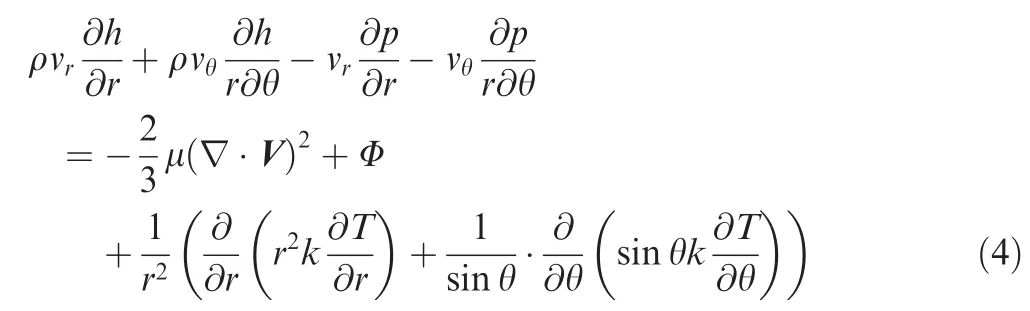
where h is the total enthalpy,p is pressure,T is temperature,μ is viscous coefficient,k is thermal conductivity coefficient,V is velocity vector,and Φ is the dissipation function.
On the stagnation line(r(θ → 0)),we have
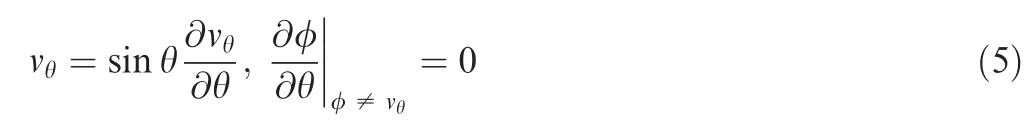
where φ is a general physical variable.
Then Eqs.(1),(2),and(4)can be further simplified as Eqs.(6)–(8).Eq.(3)involves gradients in the circumferential direction that are hard to be determined in the 1D frame and its detailed expression is not presented.
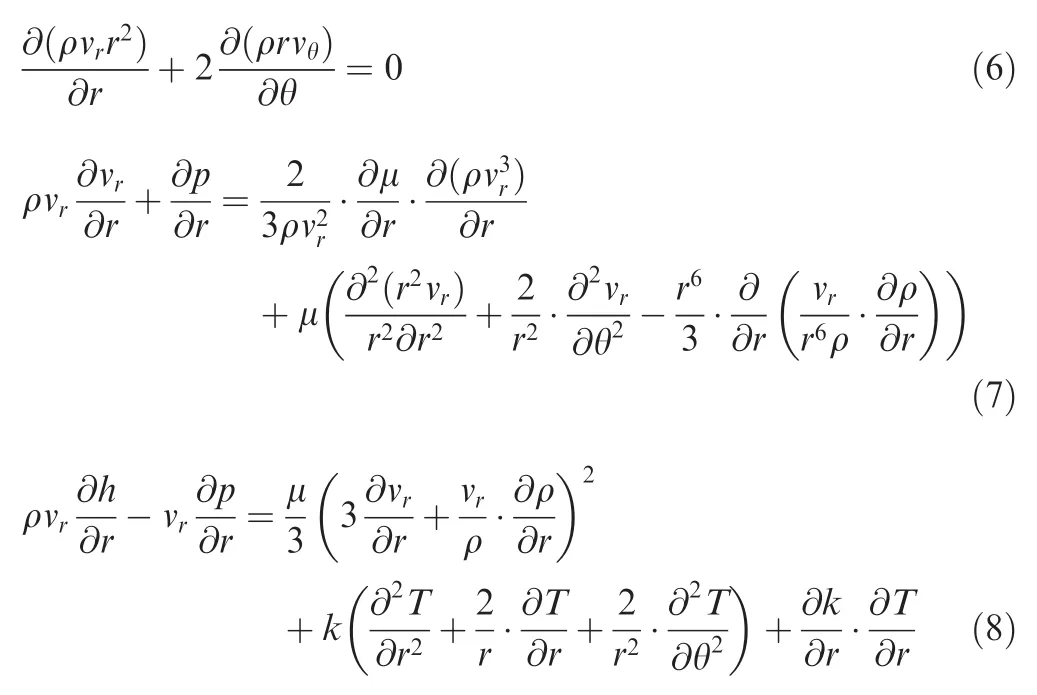
Within the boundary layer where viscosity is important,the radial velocity and temperature are nearly constant along the circumferential direction.It is reasonable to assume that
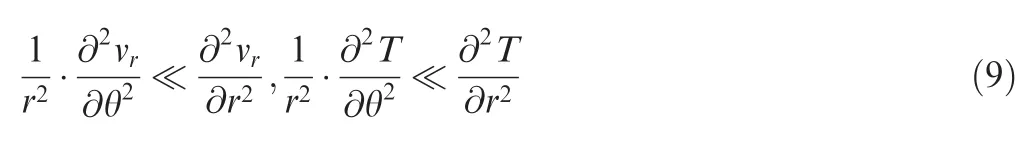
Then Eqs.(7)and(8)can be simplified into Eqs.(10)and(11).
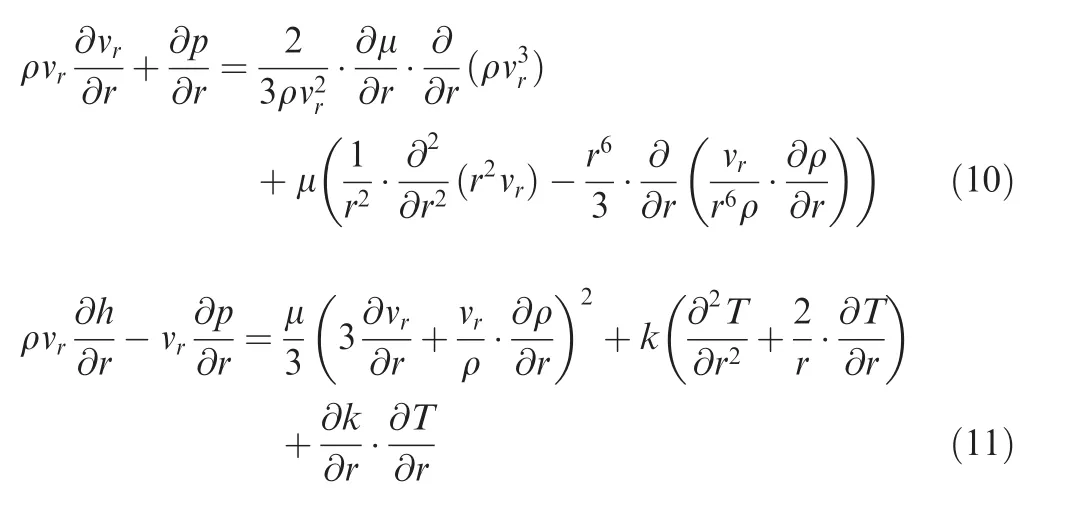
If vris prescribed,then pressure p and enthalpy h can be derived from Eqs.(10)and(11),where the density ρ relies on the constitutive relation,and coefficients μ and k have to be determined using empirical formulas.
As the flow is axial symmetric in the vicinity of the stagnation line,the circumferential velocity is zero along the stagnation line.The radial velocity vrmight be derived using the continuity equation by estimating ∂vθ/∂θ based on the momentum equation in the circumferential direction.However,it is difficult to obtain the values of involved gradients in the circumferential direction.For instance,many approximations have been made in Ref.13to estimate the involved pressure gradient.Nevertheless,the mass flux along stagnation streamline is found to decrease linearly from the shock to the stagnation point.This observation can be expressed as
where subscript ‘s” denotes the position immediately behind the shock wave.The shock stand-off distance has to be estimated,and we find that the formula(Eq.(13))proposed by Wen and Hornung11works very well:

where ρavis the average density from the shock to stagnation point.For chemically reacting flows,the density behind shock wave is not constant,so Eq.(13)takes chemical reactions into account through the averaged density.The validity of Eq.(12)will be examined in the section of model validation.
Eqs.(10)–(12)describe the pressure,enthalpy,and radial velocity along the stagnation line where the density is related to pressure and enthalpy through the constitutive relation.Thus the detailed flow is described for the stagnation streamline,which isdifferentfrom previousquasi-onedimensional models10–13where only the shock stand-off distance is interested.If the viscous effects are neglected in the present model,the momentum and energy equations can be greatly simplified,and they are expressed as follows:

Particularly,the energy equation can be written as the conservation of total enthalpy

2.2.Gas model
In principle,the gas mixture can be described by specifying the thermodynamic and transport properties of each species as well as detailed chemical mechanisms.Such description is usually complicated for typical CFD applications,but might be convenient for one-dimensional calculation.For the purpose of illustrating the quasi-one-dimensional model,however,we adopt the ideal dissociating gas(IDG)model to describe the high-temperature air for the time being.Extension to other models is expected in near future.
The ideal dissociating gas model was established by Lighthill and Freeman.They introduced the concept of the degree of dissociation in a dissociation-recombination reaction and derived the state equation with this concept for a nonequilibrium dissociating gas,which greatly simplified the analysis and calculation on non-equilibrium flow.For the air mixture,both oxygen and nitrogen would dissociate at high temperature.In view of the large difference on the characteristic dissociation temperature of oxygen(59750 K)and nitrogen(113500 K),it is reasonable to argue that significant dissociation of nitrogen would not happen if considerable amount of molecular oxygen still exists.The nitrogen is then treated as inert diluent and only oxygen-related reactions are considered in the present study.The details are shown as follows.
For a diatomic gas in chemical non-equilibrium state,its dissociation-recombination reactions can be written in a general form

where A2is the molecule and A the dissociated atom,and M represents a third body.With the degree of dissociation α(the ratio of dissociated A-atoms to the total number of A-atoms in the mixture),the equation of state,specific internal energy e and rate equation are expressed as15
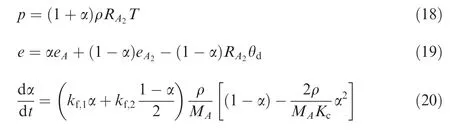
where θdis the characteristic temperature for dissociation,Kcis the equilibrium constant,and kf,1and kf,2are the corresponding rate constants offorward reactions A2colliding with A2or A,R is the gas constant of molecular oxygen,
For the air mixture considered in the present study,A2in Eq.(17)represents O2,and M can be O,O2,or N2.The degree of dissociation of oxygen is

where s is the mass fraction of oxygen in the air mixture.The mass fractions of O and O2are sα and s(1- α),respectively.Since nitrogen is treated as inert gas,its mass fraction is a constant,i.e.,1-s.Based on Eqs.(18)and(19),the equations of state and enthalpy of the gas mixture are derived as

where C= (1-s)MO2/(sMN2),ξv,O2and ξv,N2are numbers of vibrational degrees offreedom for oxygen and nitrogen,respectively.If the vibrational energy mode is assumed to be equilibrium with the translational and rotational energy modes,the number of vibrational degrees offreedom can be obtained from expression
The forward reaction rate constants can be written in the Arrheniusform askf=CfTηe-θd/Tin which η isthe temperature-dependent index.Denote kf,1,kf,2and kf,3as the corresponding rate constants for O2colliding with O,O2,and N2.According to Park’s model16,the rate constant kf,2equals kf,3.The equilibrium constant Kcis a slow-varying function of temperature and it can be represented by a characteristic density,ρd=MO2Kceθd/T/4,which is nearly a constant.15Putting together all the reaction constants,the rate equation is given as
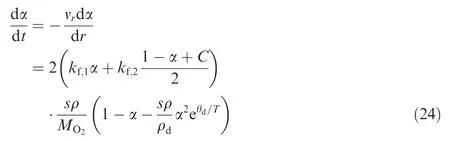
in which ρdis set to 1.5 × 105kg/m3and the parameters for kf,1and kf,2are obtained from Ref.16.
2.3.Boundary conditions
Eqs. (10)–(12) and (22)–(24) describe the quasi-onedimensional model of stagnation streamline flow with 6 unknowns ρ,p,T,h,α and vr.These equations can be easily solved using an iteration method.The calculation starts at the shock wave position and ends at the stagnation point.The shock wave is assumed to be infinitely thin,so chemical reactions are frozen when the shock is crossed.Then the post-shock flow conditions can be derived as follows:


At the stagnation point,the velocity is set to zero,and the temperature is specified with a constant value or a radial gradient.For inviscid case,the temperature condition is not needed at the stagnation point.It should be mentioned that the inviscid assumption is not valid within the boundary layer.Namely,the inviscid solution is good only from the shock location to the external edge of the boundary layer if the influence of the boundary layer on the shock stand-off distance is negligible.To estimate the effective thickness of the boundary layer δ for hypersonic flow,Wang et al.17suggested an approximate formula as follows:

where c1is a constant,ω the temperature index of viscosity,Tbthe surface temperature and T0the total temperature offree stream.The value of c1will be determined by comparing theoretical data and CFD results.
3.Model validation
The quasi-one-dimensional model describes the flow properties along the stagnation streamline.Its solution is expected to agree with the flow field from its full field solution.Such a comparison is made between the model results and CFD data in this section.
The CFD data are obtained using an in-house CFD code.The code employs the finite volume method by solving the axi-symmetric Euler or Navier-Stokes equations with chemical reactions included.The equations are solved using a fully coupled,implicit scheme based on Roe’s flux-difference splitting algorithm with the Minmod limiter.For Navier-Stokes solutions,the viscosity of each species is calculated using the kinetic theory based on collision integral as

where σ is the characteristic molecular diameter and Ωμthe viscosity collision integral.The thermal conductivity is calculated using the Eucken relation that takes into account the internal energy models,and the equivalent Prandtl number is

where γ=1+2/(3+ ξr+ ξv), ξrand ξvare the numbers of rotational degrees offreedom and vibrational degrees offreedom,respectively.The Wilke’s law is employed to evaluate the mixture values of viscosity and thermal conductivity.For example,

where
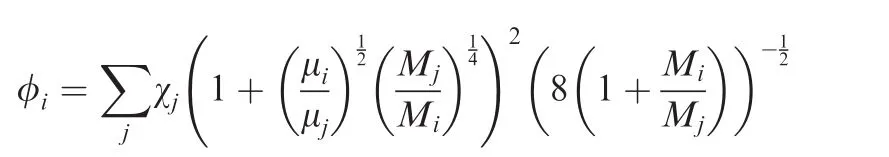
The mass diffusion coefficient is evaluated by assuming a constant Schmidt number of 0.5.Values of σ and Ωμfor air species can be found in the classic book of Anderson.18
The quasi-one-dimensional model is employed to study the hypersonic flow over a sphere with a radius of 0.305 m.The free stream is set according to the standard atmospheric condition.As for CFD simulations,mesh independent results are obtained using a structured mesh of 120 by 60 cells for inviscid cases and a structured mesh of 270 by 60 cells for viscous cases.The numerical shock thickness is found to be less than 0.3%of the radius.
A typical flow field near the stagnation streamline is shown in Fig.2 where the free stream conditions are at the altitude of 60 km.Fig.2(a)is a non-chemically reacting viscous case where stream velocity U∞and temperature T are plotted,and Fig.2(b)is an inviscid case where the pressure p and mole fraction χ0of atomic oxygen are shown.For both cases,there is a bow shock wave formed in front of the sphere and the variation offlow properties is mainly in the radial direction.

Fig.2 CFD flow field at the altitude of 60 km near stagnation streamline.
A detailed comparison between the CFD results and the present theoretical solutions is performed along the stagnation streamline for the previous two cases.Fig.3 shows the profiles of key flow properties where the density,pressure and temperature are non-dimensionalized using the post-shock values and the velocity is normalized using the free stream value.The radial coordinate is non-dimensionalized using the radius of the sphere and is labeled as¯y.The dashed vertical line is added to indicate the shock location obtained from CFD simulations.For both cases,the density and pressure increase after the shock.Particularly the pressure increase is about 10%,so the constant pressure assumption is invalid.The velocity,on the other hand,decreases to zero from the shock to stagnation point.Thus the temperature increases after the shock due to the conversion of kinetic energy to thermal energy if chemical reaction is not considered.When oxygen starts to dissociate as in Fig.3(b),part of the thermal energy is consumed during the dissociation,and then the temperature decreases after the shock.There is a thin boundary layer in the viscous case,where the temperature drops quickly to the body temperature and the density rises accordingly.When the chemical reactions are included in the inviscid case(Fig.3(b)),the oxygen dissociation rate is gradually increased from zero at the shock to the maximum at the sphere surface.Fig.3 clearly shows that the present model predicts nearly identical flow properties as the full field CFD simulations,which indicates the validity of the present model.
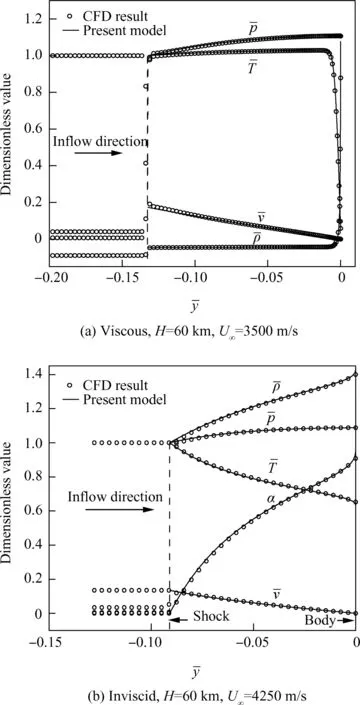
Fig.3 Comparison offlow properties along stagnation streamline.
As mentioned earlier,a linear mass flux distribution is assumed in the present model.Fig.4 shows the radial velocity vrand mass flux ρvrfor the previous cases.It is found that ρvrcalculated from CFD simulation is very close to the linear distribution,whereas vris less linearly distributed.This observation appliesto otherfreestream conditionsthatare simulated in the present study.The validity of this assumption determines the accuracy of the present model.
The applicability of the inviscid model for viscous flow is investigated as well.When the inviscid model is employed to viscous flow,the shock stand-off distance will be slightly over-estimated when Eq.(13)is adopted as the cold wall will increase the density in the boundary layer.In addition,there is a maximum degree of dissociation in viscous flow,which is due to the recombination reactions that are dominated in the boundary layer.If we focus on the maximum dissociation degree located near the external edge of the boundary layer,then the cutoff location in inviscid solution should be slightly larger than the boundary layer thickness.We find that best overall performance is achieved when the cutoff location is calculated with c1=0.38 using Eq.(28),when the body surface is non-catalytic and remains at 300 K.Fig.5 shows the flow properties along the stagnation streamline for two typical cases where the results from the inviscid model are compared with the Navier-Stokes CFD solutions.Both cases indicate that the inviscid model can predict the viscous flow with acceptable error except the boundary layer.A further comparison will be presented when we analyze the maximum dissociation degree during hypersonic flight.
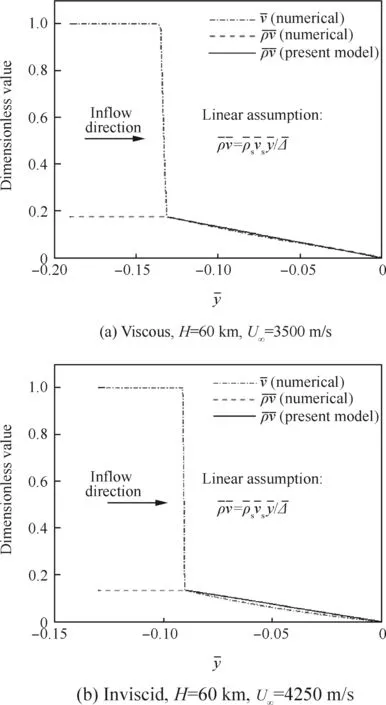
Fig.4 Velocity and mass flux along stagnation streamline.
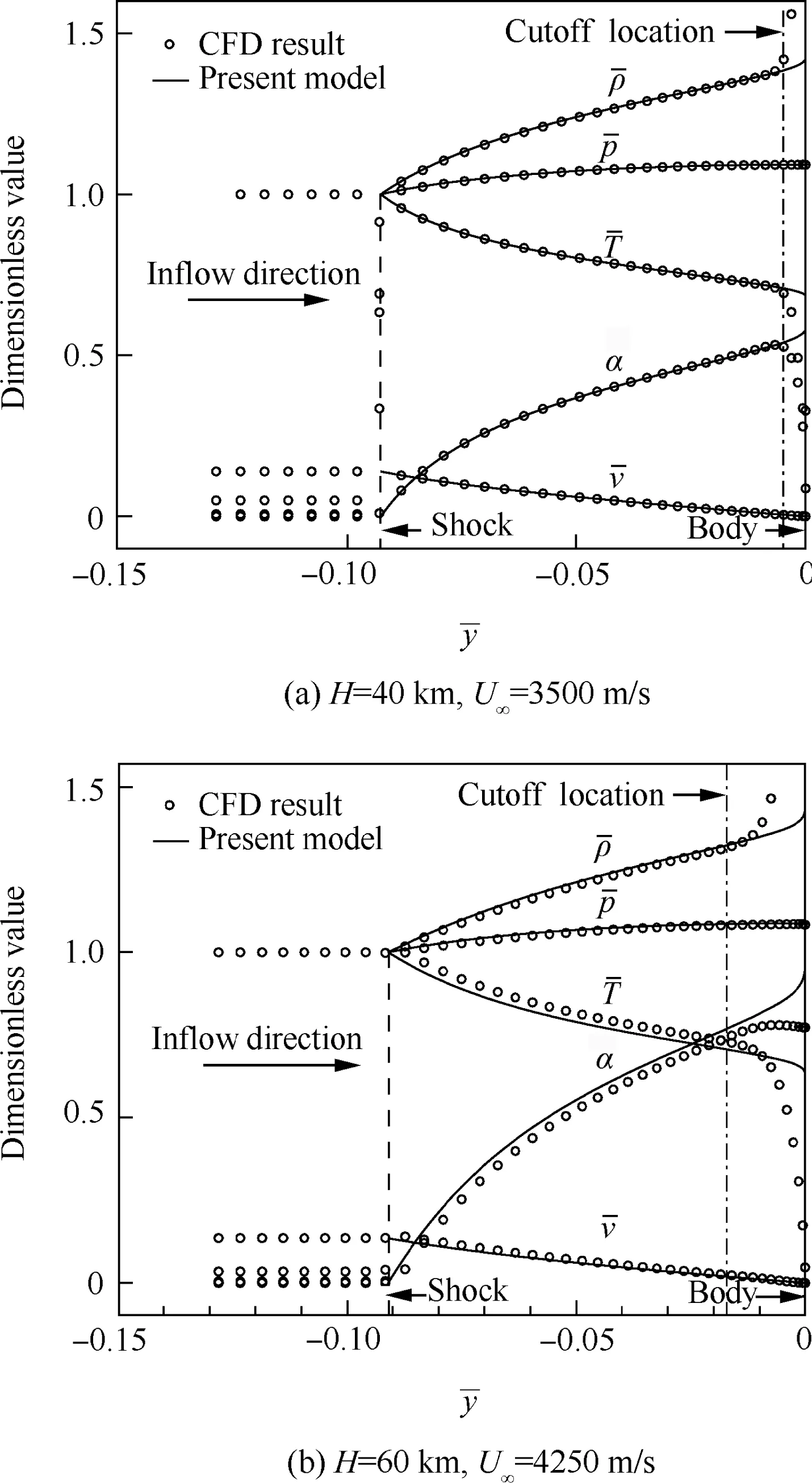
Fig.5 Comparison offlow properties along stagnation streamline(viscous results).
4.Applications
For hypersonic blunt body flow,the shock stand-off distance is a key parameter characterizing the flow structure,which is frequently studied in Refs.10–13Meanwhile,the degree of dissociation during hypersonic flight is another concerned problem because molecular dissociations consume kinetic energy that will significantly change the aerodynamics of an aircraft.In this section,the quasi-one-dimensional model is applied to studying these two problems.
4.1.Shock stand-off distance
The shock stand-off distance is the distance between the bow shock and stagnation point.The basic physical mechanisms related to this problem are quite well understood.11The accuracy of Eq.(13)has been verified in the previous section.In this subsection,we aim to illustrate the influence of thermochemical non-equilibrium on the shock stand-off distance.
When the gas behind shock wave starts to dissociate,the average density in the shock wave layer will increase,leading to a reduction in the shock stand-off distance.In order to show the influence of chemical reactions on shock stand-off distance,an equivalent reaction rate parameter,~Ω,is defined according to Belouaggadia et al.13~Ω can be related to the density gradient and has the form
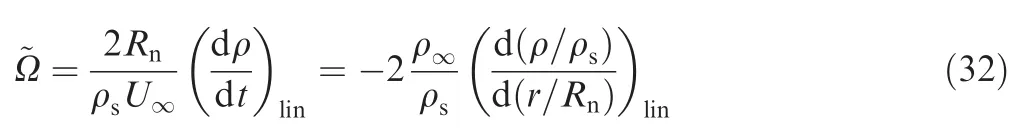
where the subscript‘lin” means that the gradient is calculated from the piecewise-linear density profile.This density gradient can be uniquely determined by equaling the area below the real density profile and a piecewise-linear approximation,which is derived as
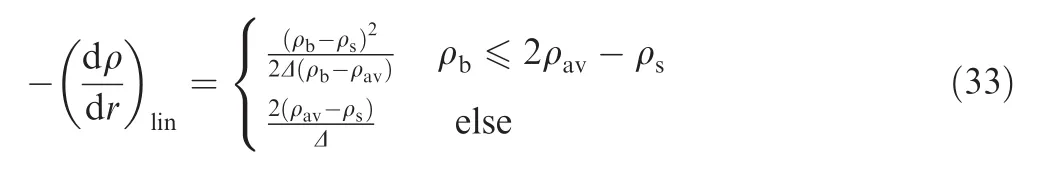
where ρbis the gas density at the stagnation point.
The quasi-one-dimensional model predicts the density distribution along the streamline,so both the shock stand-off distance and equivalent reaction rate parameter can be easily calculated.Fig.6(a)shows the shock stand-off distance at different reaction rates where ρbis obtained using the shooting method by varying the free stream velocity and reaction rate.As expected,the shock stand-off distance decreases when the reaction rate increases,which can be easily understood from Eq.(13)as chemical reactions will reduce the temperature and raise the average density.Fig.6(a)also shows that the model results agree well with the analytical solution of Wen’s theory.11
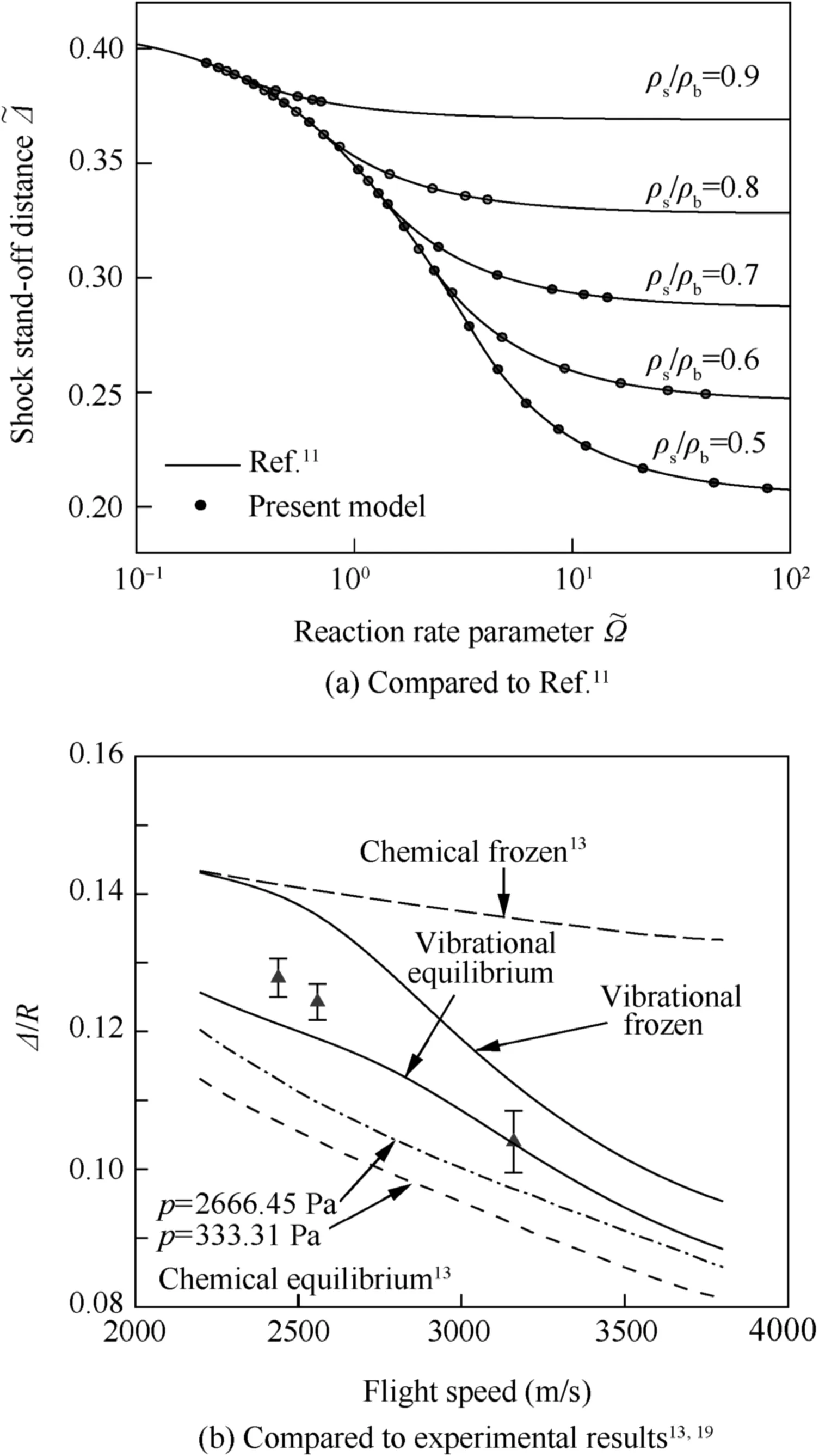
Fig.6 Shock stand-off distance comparison.
In the above calculation,the vibrational energy is assumed to be in equilibrium with the translational and rotational energy of molecules.In fact,vibrational non-equilibrium will affect the shock stand-off distance.Fig.6(b)shows the predicted shock stand-off distance for an experimental condition from Nonaka et al.19with different vibrational and chemical statuses.The experiments were performed carefully in a ballistic range for different scaling parameter ρR,while the data set with ρR=1.7 × 10-3kg/m2is chosen as a comparison with the present model.The sphere radius is fixed at 0.305 m in the model calculation.As Fig.6(b)shows,the experimental data lie between the vibrational-equilibrium and vibrationalfrozen curves,which indicates that the actual flow is in a thermal non-equilibrium state.In general,as the flight speed increases,the shock stand-off distance tends to decrease due to higher compression(stronger shock wave)and the flow approaches thermal equilibrium limit.It seems that chemical non-equilibrium has very strong influence on the shock stand-off distance as shown in Fig.6(b)where the chemicalfrozen and chemical-equilibrium lines were calculated by Belouaggadia et al.13If the temperature is high enough to cause significant nitrogen dissociation,this effect would become more severe.
4.2.Maximum degree of dissociation in stagnation region during hypersonic flight
There is a Mach number independent principle that greatly simplifies the analysis for hypersonic inviscid flow.18However,chemical reactions occurring during hypersonic flight make this principle invalid.In general,oxygen dissociation will increase with the flight speed and decrease with the altitude.The maximum degree of dissociation would reflect the importance of chemical reactions in aerodynamic evaluation.
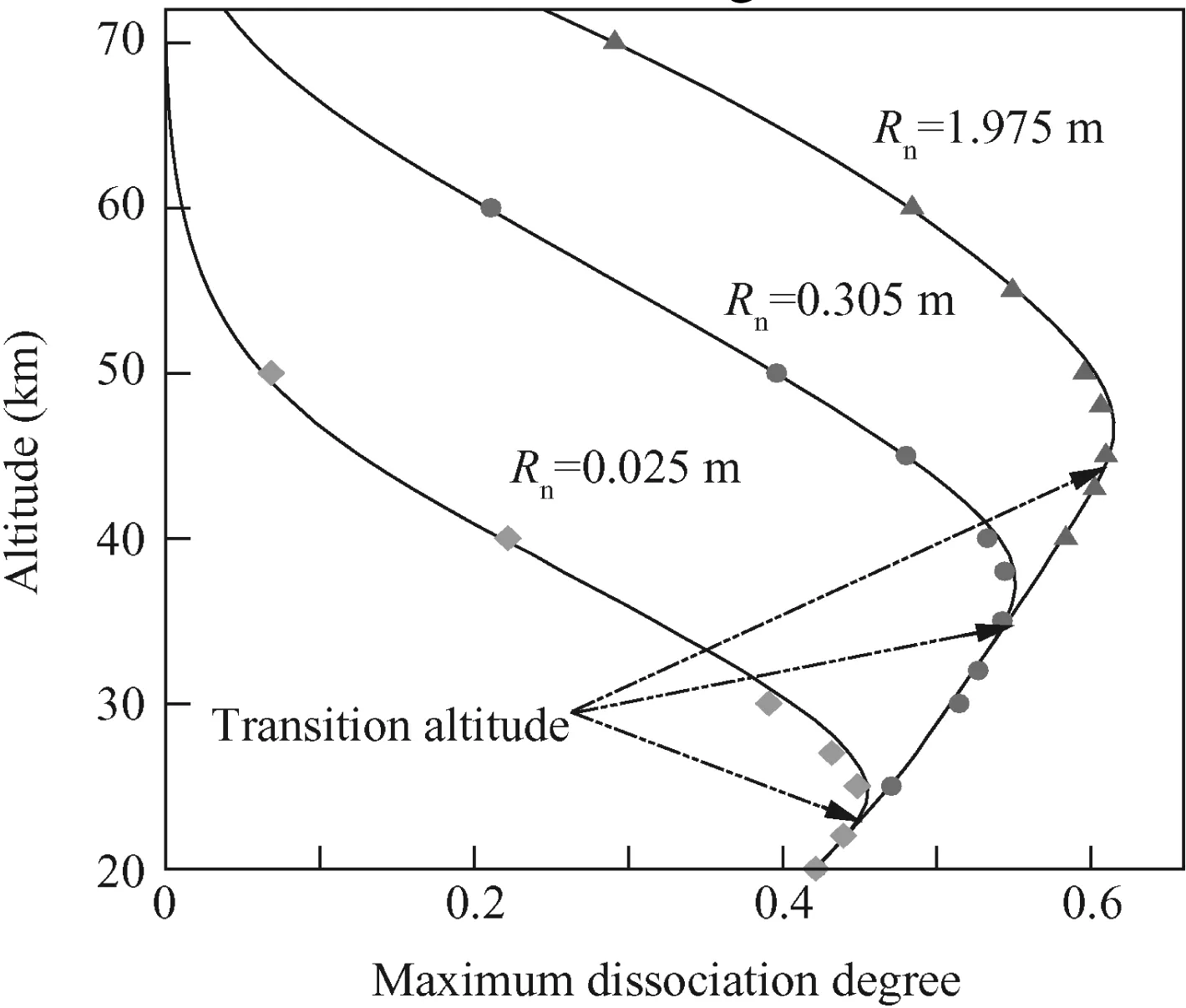
Fig.7 Maximum degree of oxygen dissociation predicted using theoretical model(line)and viscous CFD simulation(symbol),U∞=3500 m/s.
To make a detailed analysis of chemical non-equilibrium effects,airflow over a blunt body for the altitude conditions ranging from 20 to 70 km is investigated.The higher altitude is not considered as the rarefied gas effects become important where the molecular mean free path is about 0.84 mm at 70 km.The flight speed is set to be 3500 m/s,and three nose radii,i.e.,Rn=1.975 m,0.305 m,and 0.025 m,are chosen for the calculations.The calculated maximum dissociation degree is presented in Fig.7 for both the quasi-onedimensional model and CFD simulation.It turns out that the agreement between theoretical and CFD results is quite satisfactory.From Fig.7,the maximum dissociation degree varies with the radius of blunt body in general.With a given radius,the dissociation increases with the altitude at first and decreases thereafter.This behavior of dissociation is attributed to two competing factors:equilibrium shift of chemical reactions in Eq.(17)and non-equilibrium effects.With the finite rate chemistry,the dissociation increases along the streamline until it reaches chemical equilibrium.Thus the maximum dissociation degree in the flow depends on the equilibrium dissociation degree and the allowed relaxation distance of chemical reaction.When the flight altitude increases,chemical equilibrium will shift to the direction that tends to increase the density,which enhances the dissociation and increases the equilibrium dissociation degree.The relaxation distance will also increase with the altitude whereas the shock stand-off distance varies little.Thus the ratio of shock stand-off distance(Strictly speaking,it should minus the boundary layer thickness.)to the relaxation distance decreases with the altitude.The altitude when this distance ratio is unit can be defined as the transition altitude.This transition altitude increases with the nose radius because the shock stand-off distance is proportional to the radius.Below the transition altitude,the maximum dissociation degree is the equilibrium dissociation degree that is independent of the radius.Above the transition altitude where the distance ratio is less than one,the maximum dissociation degree is only a fraction of the equilibrium dissociation degree and this fraction decreases with the altitude.It should be mentioned that the largest value of the maximum dissociation degree is achieved at an altitude above the transition altitude due to the competition between equilibrium shift and non-equilibrium relaxation.If the altitude is high enough,the maximum dissociation degree decreases with the altitude as the non-equilibrium effects become dominant.Fig.7 also shows that the dissociation for smaller blunt body is less significant at the chemical non-equilibrium altitude.It should be mentioned that the Knudsen number for the small nose case(Rn=0.025 m)is about 0.033 at altitude 70 km and rarefied gas effects are important.However,rarefied gas effects will reduce the dissociation degree,which will not have obvious effect on the related data since their dissociation degree is already negligible.
For engineering purpose,it is interesting to have an overall plot for the maximum degree of oxygen dissociation in the flight and altitude coordinates.To be consistent with the above cases,the nose radius of the blunt body is fixed at 0.305 m.The computation covers the range of the flight speed from 2000 m/s to 5300 m/s and the altitude from 20 km to 70 km.The speed and altitude intervals are set to be 50 m/s and 1 km,respectively.It takes about several minutes to complete all the calculations using the quasi-one-dimensional model on a single PC.
Fig.8(a)shows the contours of the maximum degree of oxygen dissociation α during the flight.In the plot the oxygen dissociation region predicted by Hansen and Heims1using the early equilibrium model is also added as the shadowed region between the dash-dot lines where the dissociation decreases monotonically with the altitude.To identify the oxygen dissociation region from our calculation,it is regarded that oxygen dissociation is negligible when α < 1%and it will enter into the nitrogen dissociation region when α > 95%.The oxygen dissociation region predicted by the present model agrees with the early equilibrium model at altitude below the equilibrium/non-equilibrium transition line.The dissociation region above the transition line,however,bends to the larger speed side at higher altitude because more kinetic energy is needed to have the same level of dissociation when chemical non-equilibrium occurs.Therefore,the oxygen dissociation region in the speed and altitude plot will be essentially different from that given by the equilibrium gas model.
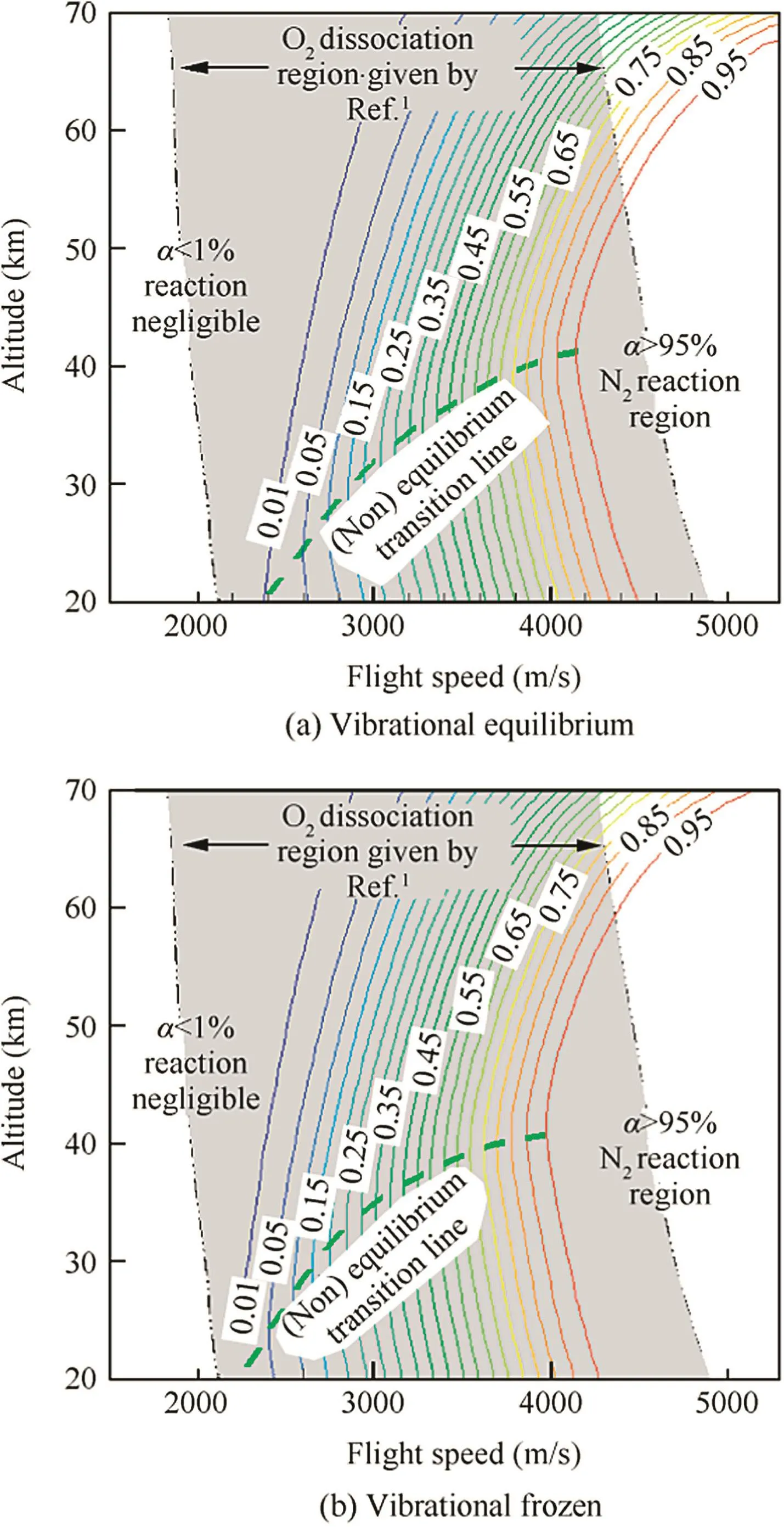
Fig.8 Maximum degree of oxygen dissociation during hypersonic flight for a sphere(Rn=0.305 m).
It should be mentioned that the data in Fig.8(a)are obtained with the assumption of thermal equilibrium.If the vibrational energy of molecules is frozen,the dissociation contours will shift to the lower speed side by an average value about 300 m/s as shown in Fig.8(b),because the temperature will increase when the vibrational energy model is frozen and thus enhances the dissociation.However,the difference between Fig.8(a)and(b)is not obvious,which indicates that the thermal non-equilibrium effect is not critical for the current evaluation of oxygen dissociations.It should also be noted that the present model employs the ideal dissociating gas model.Further improvement to the model could be made by using species equations to replace the ideal dissociating gas model.Thus advanced physical-chemical models can be evaluated or tested using experimental data such as the shock stand-off distance.For instance,state-to-state vibrational-chemical kinetics has been proposed to couple with gas dynamics to fully understand the non-equilibrium hypersonic reacting flows.20The large computational cost,however,has prevented detailed numerical simulation of multi-component reacting flows with the use of the state-to-state kinetic model.
5.Conclusions
Hypersonic flow involves complex physical and chemical processes,which requires various approaches to understand their behavior.Quasi-one-dimensional study can be a good complement to CFD simulation and experimental investigation.The concluding remarks of this work are as follows:
(1)A quasi-one-dimensional model is proposed to study the chemical non-equilibrium flow along the stagnation streamline over blunt body.Detailed comparison with full field CFD simulation demonstrates that the present model is able to recover the flow along the stagnation streamline with acceptable error.
(2)The model calculation is proved to be very efficient and can be used to evaluate the flow characteristics along the stagnation streamline under various flight conditions,including the shock stand-off distance and oxygen dissociation.
(3)The surface heat flux can be obtained at the stagnation point through the quasi-one-dimensional model,which might provide a calibration value for CFD calculation where meshes are usually not fine enough.
Acknowledgments
This work was supported by the National Natural Science Foundation of China(Nos.1372325 and 91116013).
1.Hansen CF,Heims SP.A review of the thermodynamic,transport,and chemical reaction rate properties of high-temperature air.Washington,D.C.:NASA;1958.Report No.:NACA TN 4359.
2.Gupta RN,Yoss JM,Thompson RA,Lee KP.A review of reaction rates and thermodynamic and transport properties for an 11-species air model for chemical and thermal non-equilibrium calculations to 30000 K.Washington,D.C.:NASA;1990.Report No.:NACA TN 1232.
3.Park C.Hypersonic aerothermodynamics:past,present and future.Int J Aeronautical Space Sci 2013;14(1):1–10.
4.Sun QH,Zhu HY,Wang G,Fan J.Effects of mesh resolution on hypersonic heating prediction.Theor Appl Mech Lett 2001;1(2):37–40.
5.Freeman NC.Non-equilibrium flow of an ideal dissociating gas.J Fluid Mech 1958;4(4):407–25.
6.Lighthill MJ.Dynamics of a dissociating gas.Part 1:equilibrium flow.J Fluid Mech 1957;2(2):1–32.
7.Lick W.Inviscid flow of a reacting mixture of gases around a blunt body.J Fluid Mech 1960;7(1):128–44.
8.Belotserkovskii OM,Dushin VK.The supersonic flow round blunt bodies of an unbalanced stream of gas.USSR Comp Math Math Phys 1964;4(1):83–104.
9.Kyriss CL.A time dependent solution for the blunt body flow of a chemically reacting gas mixture.Reston:AIAA;1970.Report No.:AIAA-1970-0771.
10.Hornung HG.Non-equilibrium dissociating nitrogen flow over spheres and circular cylinders.J Fluid Mech 1972;53(1):149–76.
11.Wen CY,Hornung HG.Non-equilibrium dissociating flow over spheres.J Fluid Mech 1995;299(1):389–405.
12.Olivier H.A theoretical model for the shock stand-off distance in frozen and equilibrium flows.J Fluid Mech 2000;413:345–53.
13.Belouaggadia N,Olivier H,Brun R.Numerical and theoretical study of the shock stand-off distance in non-equilibrium flows.J Fluid Mech 2008;607:167–97.
14.Chen S,Sun QH.Analysis of maximum dissociation degree of oxygen during hypersonic flight.Chinese J Theo Appl Mech 2014;46(1):20–7.
15.VincentiWG,Kruger CH.Introduction to physicalgas dynamic.New York:John Wiley and Sons,Inc.;1965.
16.Park C.Assessment of two-temperature kinetic model for ionizing air.J Thermophys Heat Transfer 1987;3(3):233–44.
17.Wang ZH,Bao L,Tong BG.Rarefaction criterion and non-Fourier heat transfer in hypersonic rarefied flows.Phys Fluids 2010;22(12),126103-1-7.
18.Anderson JD.Hypersonic and high temperature gas dynamics.2nd ed.Virginia:AIAA Inc.;2006.
19.Nonaka S,Mizuno H,Takayama K.Measurement of shock standoff distance for sphere in ballistic range.J Thermophys Heat Transfer 2000;14(2):225–9.
20.Kunova O,Nagnibeda E,Sharafutdinov I.State-to-State and simplified models for shock heated reacting air flows.AIP conference proceedings 2014;1628:1194–201.
Chen Song is a Ph.D.candidate at Institute of Mechanics,University of Chinese Academy of Sciences.He received his B.E.degree from Wuhan University of Technology in 2010.His current research interests are applied aerodynamics,computational fluid dynamics and combustion.
Sun Quanhua is a research professor at Institute of Mechanics,Chinese Academy of Sciences,and a professor at University of Chinese Academy of Sciences,China.He received his Ph.D.degree from the University of Michigan in 2003.His research area includes rarefied gas dynamics,computational fluid dynamics,hypersonic aerodynamics,plasma flow and combustion.
29 September 2015;revised 28 January 2016;accepted 22 March 2016
Available online 20 October 2016
Quasi-one-dimensional model;
Hypersonic;
Non-equilibrium;
Stagnation flow;
Shock stand-off distance
Ⓒ2016 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is anopenaccessarticleundertheCCBY-NC-NDlicense(http://creativecommons.org/licenses/by-nc-nd/4.0/).
*Corresponding author at:State Key Laboratory of High Temperature Gas Dynamics,Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China.
E-mail addresses:chensong212@hotmail.com(S.Chen),qsun@imech.ac.cn(Q.Sun).
Peer review under responsibility of Editorial Committee of CJA.
Production and hosting by Elsevier
http://dx.doi.org/10.1016/j.cja.2016.09.004
1000-9361Ⓒ2016 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.
This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
 CHINESE JOURNAL OF AERONAUTICS2016年6期
CHINESE JOURNAL OF AERONAUTICS2016年6期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Analysis of swirling flow eff ects on the characteristics of unsteady hot-streak migration
- Implicit discontinuous Galerkin method on agglomerated high-order grids for 3D simulations
- Design and implementation of rigid-flexible coupling for a half-flexible single jack nozzle
- Dynamic simulation of aerial towed decoy system based on tension recurrence algorithm
- An experimental investigation on static directional stability
- Transonic wing stall of a blended flying wing common research model based on DDES method
