超越方程组求解喷淋系统阻力

曹 鸿 龙

(上海启合印建筑设计有限公司，上海 200062)



超越方程组求解喷淋系统阻力

曹 鸿 龙

(上海启合印建筑设计有限公司，上海 200062)

介绍了几种喷淋系统水力计算的方法，对房间布局及管道连接方式进行了分析，采用超越方程组法，按最不利情况求解喷淋系统阻力，研究了末端压力对算法的影响，并阐述了超越方程组法的计算流程，针对实际工程设计中存在的问题，提出了相应的处理建议。

喷淋系统，水力计算，超越方程组

当今高层建筑乃至超高层建筑，比较常见的最不利楼层(一般为最高楼层)多为办公生活区，即中危险Ⅰ级区，按照GB 50084—2001自动喷水灭火系统设计规范(2005版)规定，其设计喷水强度为6 L/(min·m2)，作用面积为160 m2，喷头工作压力为0.10 MPa，本文仅针对此种常见情况进行分析说明。喷淋系统简图见图1。

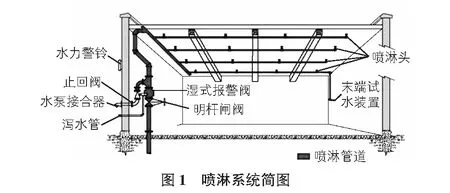
以往我们在进行自动喷水灭火系统的水力计算时，一般采用作用面积法或特性系数法，为方便计算，上述两种方法均有其计算假设，与实际有所出入。下面我们针对几种计算方法做简要分析。

1 喷淋系统水力计算方法概述

1.1 作用面积法

作用面积法是《自动喷水灭火系统设计规范》推荐的计算方法，其根本的目的在于抑制一定面积下火灾的蔓延，保证喷水强度不小于规范规定强度，此处计算时假设作用面积内每只喷头的喷水量相同且均以最不利前喷头喷水量取值。此假设实际上减小了作用面积内的喷水量，亦间接减小了喷淋系统的阻力。

1.2 特性系数法

特性系数法是从系统设计的最不利点喷头开始，沿程计算各喷头的压力、喷水量、管段累积流量、水头损失直至管段累积流量达到设计流量为止，之后的管段流量不再累积，只计算水头损失。此处假设在达到设计流量时，喷头所保护的面积至少已经满足规范所规定的保护面积。此假设实际上很难满足实际的设计需要，很大程度上受到建筑布局影响。

1.3 超越方程组法

超越方程组法是在优先满足保护面积的前提条件下，不做任何假设，从系统最不利点喷头开始计算，采用超越方程组沿程计算各喷头的压力、喷水量、管段累积流量、水头损失直至完成保护面积内所有喷头的计算为止，保护面积之外的喷头不计算流量，只计算水头损失。

2 房间布局及管道连接方式分析

2.1 房间布局

上述三种方法都会受到房间布局及管道连接方式的影响，但针对常规功能建筑，常规布局，中危险Ⅰ级所保护的面积为160 m2，正方形布置喷头间最大间距3.6 m，距离墙边1.8 m。按装修情况下普通石膏板吊顶布置下垂型喷头，由图2可知在最大距离布置下，12个喷头最大的保护面积为14.4×10.8=155.52 m2，而需要保护160 m2相应的作用面积，则出现向长方向或向宽方向两个方向加长的变化。由图3易知，当宽方向加长时，作用面积达到160 m2，喷头数增加到最不利的16只。且当喷淋系统的最不利点处在图3的开敞空间时，按规范要求开放的喷头数达到最不利的16只。

2.2 管道连接方式

由于不同的管道连接方式会造成沿程水头损失的不同，在求解超越方程组的过程中，每个喷头前后的边界条件不同，得出的结果便会逐级变化，影响最终结果。管道的连接方式往往由于主观原因而不同，以图3的喷头布置方式来讲，会有大体上三种连接方式，如图4所示。在已知喷淋立管在本区域左侧方向时，易知连接方式1和连接方式2所导致的管道计算当量长度是相同的且都小于连接方式3。管道连接方式3主观的加长了最不利区域的管道当量长度，虽然最不利区域后的干管长度有所减少，但影响小于在最不利区域内产生的阻力。

3 最不利管段水力计算

首先在这里确定喷头的流量系数为K=80，最不利点处喷头的工作压力为0.10 MPa，喷淋系统需要保护的面积为160 m2，作用面积内至少达到6 L/(min·m2)的喷水强度。忽略各计算节点处由于喷头安装而使用的末端异径弯头和可能出现的延长管对计算结果的影响。据《美国工业防火手册》介绍：“经过实测，自动喷水系统管道在使用20年～25年后，其水头损失接近设计值[1]，及Hazen-Williams(海登—威廉)公式结果”。在此沿程水头损失采取GB 50974—2014消防给水及消火栓系统技术规范中10.1.2.1的方法[2]进行计算，其相应公式如下:

(1)

(2)

(3)

μ=ρv

(4)

(5)

其中，λ值取自超越方程组的数值解，λ采用迭代法计算；ε按镀锌钢管取0.000 15；di为管道内径，其值取管径减1 mm；ρ为水的密度，取999.7 kg/m3；T为水温，取10 ℃。

喷头的出流量公式为：

(6)

其中，K取80，对于喷头a的P取0.1 MPa，得q=80 L/min，即4/3 L/s。

计算过程中，由于实际安装时使用到的弯头、三通等管件同样会产生相应阻力而影响计算结果，我们这里采用当量长度法折算管件的影响，其相应数据取自GB 50974—2014表10.1.6-1。本案例中管段a-f的总当量长度为23.6，总水损25.88 m；管段a1-f的总当量长度18，总水损23.7 m，无最不利点倒挂现象，故节点a为最不利点。

由于最不利点压力已知，管段a-f可以由式(1)～式(6)逐步计算直至节点f。对管段a1-f来讲，这时我们已知节点f的压力，各管段的管径及当量长度，需要计算转输流量。此处我们需要建立24元超越方程组(本案例中每个管段和节点的节点流量q，管段流量Q，节点压力P，管道流速v，沿程损失阻力系数λ，水力坡度i均为未知数)，利用MATLAB计算软件优化求解[3]方程组的数值解。得到转输流量后采用同样计算方法得出相应管段转输流量，继续完成后续管段f-g，g-h及h-3的计算得到节点g，h的压力。详细计算数据见表1。

由上述计算列表得出h-3管段之后，最不利流量认为恒定，对应DN80的i值为0.590 921 2 mH2O/m；对应DN100的i值为0.182 354 8 mH2O/m；对应DN150的i值为0.022 087 4 mH2O/m。系统设计流量30.85 L/s，系统的理论设计流量160×6/60=16 L/s，区域内平均喷水强度30.84×60/160=11.565 L/(min·m2)，最不利点附近4个喷头的平均喷水强度(1.33+1.49+1.47+1.64)×60/(6.4×6.25)=8.895 L/(min·m2)。

按原喷淋规范计算公式可得最不利点压力为0.10 MPa时保护区域入口3处的总流量为31.44 L/s，压力为67.49 mH2O。对比后不难发现，新公式的流量计算结果略小于原公式，但水头损失减少10余米。

4 超越方程组法计算

表1 各管段及节点计算表(0.10 MPa)

4.1 末端压力对算法的影响

无论是作用面积法还是特性系数法，其最不利点的压力由于其计算方式的限定都是以0.1 MPa为基准进行计算的，而实际不难看出，仅此保护区内所需要的压力就超过了0.5 MPa，实际流量超过30 L/s，平均喷水强度也达到了设计值的近2倍。

根据设计要求，我们应该满足保护区域内的平均喷水强度不低于设计喷水强度，最不利点周围4个喷头的平均喷水强度不低于设计喷水强度的85%[4]。又有GB 50084—2001(2005年版)表5.0.1内备注“系统最不利点处喷头的工作压力不应低于0.05 MPa”的规定。此处取最不利点喷头保护半径1.6 m计，则最小压力值为[(1.6×2)2×6/80]2/10=0.058 98 MPa，再进行计算，计算结果见表2。

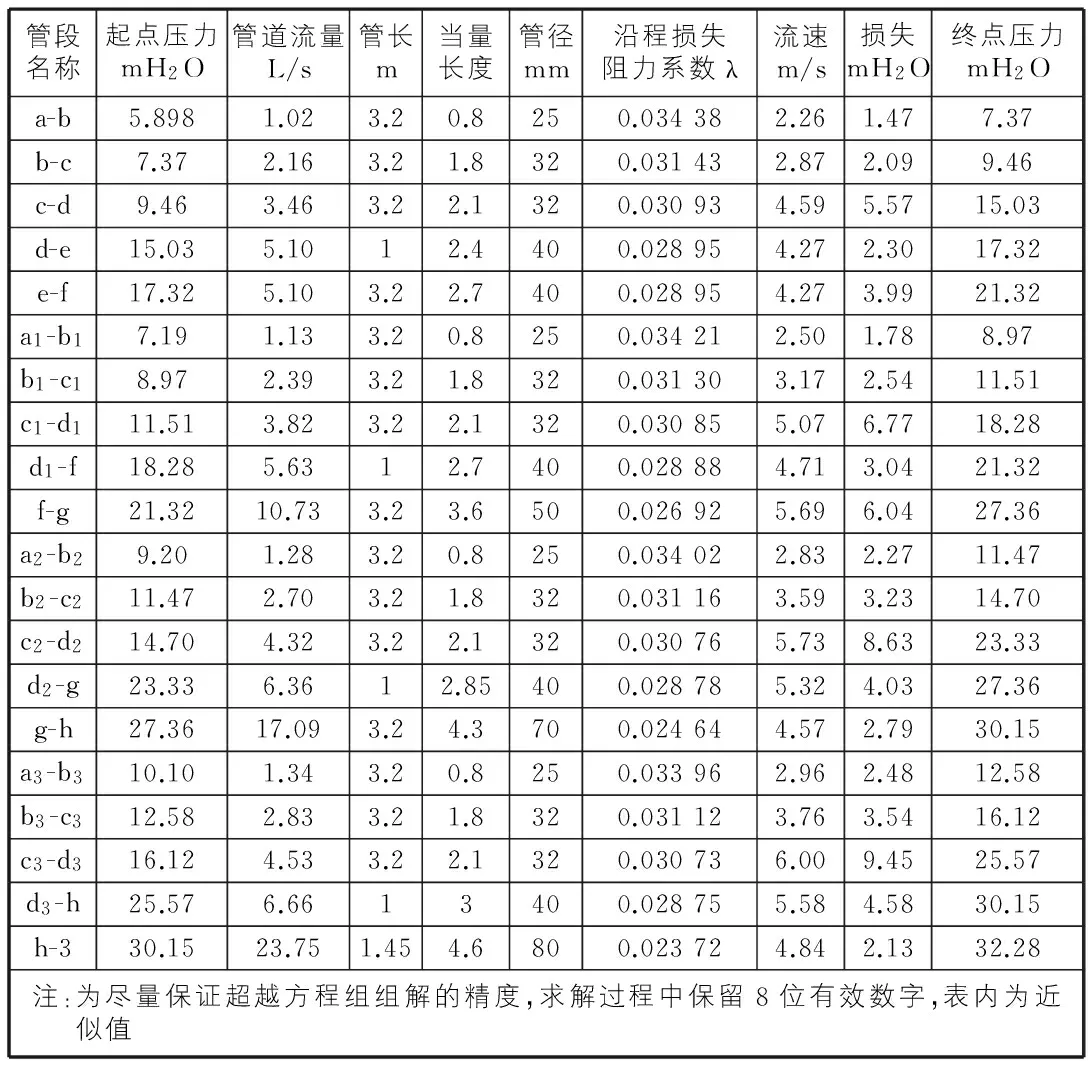
表2 各管段及节点计算表(0.058 98 MPa)

h-3管段之后，最不利流量认为恒定，对应DN80的i值为0.352 318 1 mH2O/m；对应DN100的i值为0.109 040 4 mH2O/m；对应DN150的i值为0.013 313 1 mH2O/m。实际喷水强度23.75×6/160=8.9 L/(min·m2)，大于设计值。最不利点附近4个喷头的平均喷水强度(1.02+1.14+1.13+1.26)×60/(6.4×6.25)=6.825 L/(min·m2)，满足设计要求。

按原喷淋规范计算公式可得最不利点压力为0.589 8 MPa时保护区域入口3处的总流量为24.68 L/s，压力为40.92 mH2O。对比后仍然不难发现，新公式的流量计算结果略小于原公式，但水头损失减少约7 m。

故对于本文中的案例，假设采取喷淋水泵直接从消防水池吸水的给水方式时，则应选取的喷淋泵理论扬程为：Hb=Z+∑hx+L150×0.013 313 1+L100×0.109 040 4+L80×0.352 318 1+32.28。其中，Hb为水泵扬程；Z为喷淋最不利点高度与消防水池最低有效水位高度间的几何高差；∑hx为水泵吸水口到最不利层水流指示器后的总水头损失(包括信号阀及水流指示器)；L150为最不利层水流指示器后到节点3前DN150的喷淋干管长度；L100为最不利层水流指示器后到节点3前DN100的喷淋干管长度；L80为最不利层水流指示器后到节点3前DN80的喷淋干管长度。水泵理论流量为23.75 L/s。

4.2 计算流程

对于超越方程组法，有以下计算流程：

1)确定实际工程的危险等级，以及其对应所需要保护的面积和形状。

2)明确保护区域内喷头位置和管道连接方式，列出每段管道当量长度详表。

3)确定最不利作用点，根据其实际保护半径计算其最小所需压力，但不小于0.05 MPa。

4)用顺序方法求解各管段参数至第一分叉点。

5)列出超越方程组，并利用计算工具求解第一分叉点另外一端的各管段参数。

6)顺序计算至下一分叉点。

7)重复第5)步，第6)步直至完成保护区域内所有管段参数的计算。

8)验证喷淋系统最不利点喷头开始作用时(此处假定节点h之后到水流指示器的水头损失因流量变化而减小的部分忽略不计)，其工作压力是否满足0.1 MPa。

对于本文中讨论的情况，有验证结果，当火灾开始时，最不利点处喷头工作压力为0.206 MPa，流量为1.91 L/s，满足喷淋试水要求。

5 实际工程设计中的相关问题及建议

5.1 实际开放喷头数的影响

由于房屋造型多种多样，最不利保护区域内开放喷头的数量受到房屋构型的影响可能出现最少需要13个喷头的情况，此时设计流量和喷水强度则会小于本文中所讨论的情况，在设计计算过程中要注意喷水强度是否可以满足要求。

5.2 非最不利层消防时的影响

非最不利层消防时，由于减压孔板(或减压阀组)的局限性，一般会使得压力比最不利层稍大，此时实际喷水强度和喷水流量会大于设计值，导致实际消防时间变小。此情况也与发生在最不利层的非最不利区域等效。

5.3 末端压力选取对设计的影响

直接按0.05 MPa计算及0.10 MPa校核虽能满足火灾初期的喷水要求，但其中在火灾末期其0.05 MPa的工作压力并不一定能保证喷头的布置间距内水膜的全覆盖。当然，此问题还与喷头布置高度、障碍物遮挡以及火灾发生位置有关。所以最佳办法是按喷头布置最不利间距先计算出末端所需压力，再以此压力为基准完成计算和校验。

5.4 工程设计计算时要注意的事项

超越方程组法虽能准确反映火灾时各喷头和管段的动作情况，但是不可否认此方法的计算难度明显大于其他两种计算方法，实际工程中还需要结合工程实际，参照工程的性质及设计标准来选择较为合适的计算方法。

[1] GB 50084—2001，自动喷水灭火系统设计规范(2005年版)[S].

[2] GB 50974—2014，消防给水及消火栓系统技术规范[S].

[3] 徐艳东，孟晓刚.MATLAB函数库查询词典[M].北京：中国铁道出版社，2005：429.

[4] 王增长.建筑给排水工程[M].第5版.北京：中国建筑工业出版社，2005：86.

Transcendental equations for solving the resistance of spray systems

Cao Honglong

(ShanghaiQiheyinArchitectsStudioLtd,Shanghai200062,China)

The paper introduces hydraulic calculation methods of several spray systems, analyzes housing layout and pipeline connection methods, applies transcendental equations for solving the resistance of spray system under the worst condition, studies the impact of end pressure upon computation method, and escribes the calculation procedures of transcendental equations. In light of problems existing in actual engineering design, it puts forward corresponding processing suggestions.

spray system, hydraulic calculation, transcendental equations

1009-6825(2016)05-0128-04

2015-12-03

曹鸿龙(1983- )，男，工程师

TU991.41

A