一种基于多示例学习的动态样本集半监督聚类算法

李学贵 许少华,2 李 娜 于文韬

(1.东北石油大学计算机与信息技术学院，黑龙江 大庆 163318； 2.山东科技大学信息科学与工程学院，山东 青岛 266590；3.中国石油大庆油田化工有限责任公司东昊分公司，黑龙江 大庆 163312)

一种基于多示例学习的动态样本集半监督聚类算法

李学贵1许少华1,2李 娜3于文韬1

(1.东北石油大学计算机与信息技术学院，黑龙江 大庆 163318； 2.山东科技大学信息科学与工程学院，山东 青岛 266590；3.中国石油大庆油田化工有限责任公司东昊分公司，黑龙江 大庆 163312)

针对时域空间动态样本模式分类和标记信息的有效利用问题，提出了一种基于多示例学习的动态样本半监督聚类算法。根据时间信号的结构关系和模态特征，建立动态样本的多示例信息表示模型；通过定义一种可度量时变函数样本包间近似度的广义Hausdorff距离和基于近邻传播的聚类原则，构建多示例动态样本包的半监督聚类算法。算法利用样本包的类别先验知识构建样本集初始划分种子簇并探索样本的分布特征，采用基于广义Hausdorff距离的近邻传播策略调整样本包聚类，突出动态指标局部模态变化特征在样本分类中的差异性。以油田地质研究中测井曲线油层水淹状况判别为例，验证了模型和算法的有效性。

油层水淹状况判别 聚类算法 时变函数集合 半监督学习 多示例模型

非平稳动态信号的分类和辨识一直是信息处理方法研究中的一个重要方向。由于实际中时变采样信号模态变化的多样性和随机性，一些非线性系统产生的过程信号常常表现出多峰性、交遇性和整体特征的模糊性，给信号的识别和分析带来困难。一些情况下，同类动态信号样本模态特征之间有着较大的歧义性或存在反例，而不同类信号样本的形态特征差异却很小，致使现有许多自动分析方法和模型的鲁棒性和辨识精度低、泛化性质不稳定。因此，如何突出并拾取信号样本特征的差异性，有效利用标记样本的先验知识，已成为复杂信号分类处理中一个迫切需要解决的问题[1,2]。

近几年，多示例和半监督的学习方法受到广泛关注，在细节分析、局部特征提取及标记信息的有效利用等方面表现出优势，并成功应用于药物分子的活性分析、图像识别与检索及文本分类与模式匹配等实际领域[3～9]。如果将多示例和半监督的学习机制与动态信号模式识别方法相结合，建立起一种融合不同方法优势的信息模型，则在机制上可提高对非平稳复杂信号的辨识和分析能力。

聚类分析是一种典型的非监督机器学习和数据分析方法，在工程领域和科学研究中有着广泛的应用[10,11]。笔者将半监督与多示例的学习框架向时域空间扩展，针对动态样本的聚类和分类问题，提出一种基于多示例学习的时变函数样本集半监督聚类算法。首先根据系统时间信号的结构特征，建立动态样本的多示例信息表示模型；然后针对多示例模型，构建一种可度量动态函数样本包间距离的广义Hausdorff测度范数，并基于该泛数和近邻传播策略建立多示例动态样本的半监督聚类算法。算法利用已标记样本的类别信息构建动态样本集不相交的初始划分种子簇，采用近邻传播策略实现样本的聚类分类和未标记样本的标识。以石油地质研究中基于测井曲线的油层水淹状况判别为例，实际资料处理结果表明，该算法有效提高了聚类判别的准确性。

1 动态样本的多示例表示模型和半监督学习

1.1 动态样本的多示例表示模型

多示例学习(Multiple-Instance Learning,MIL)被认为是和监督学习、非监督学习、强化学习并列的一种学习框架[12]。在多示例学习中，样本被分割为由多个示例构成的样本包，每个示例展现了样本不同方面的性质。集合中只有包具有标记，而示例不具备标签。MIL针对样本包中每个示例进行学习，在机制上可有效突出指标变量的细节特征并滤除包中反例引起的歧义性。

笔者将多示例学习框架推广到时域空间。对于时变函数集合，多示例模型是将每个时间数据对象表示为包含多个时间过程示例的样本包，训练为针对每个时间函数示例的学习过程，如图1所示。

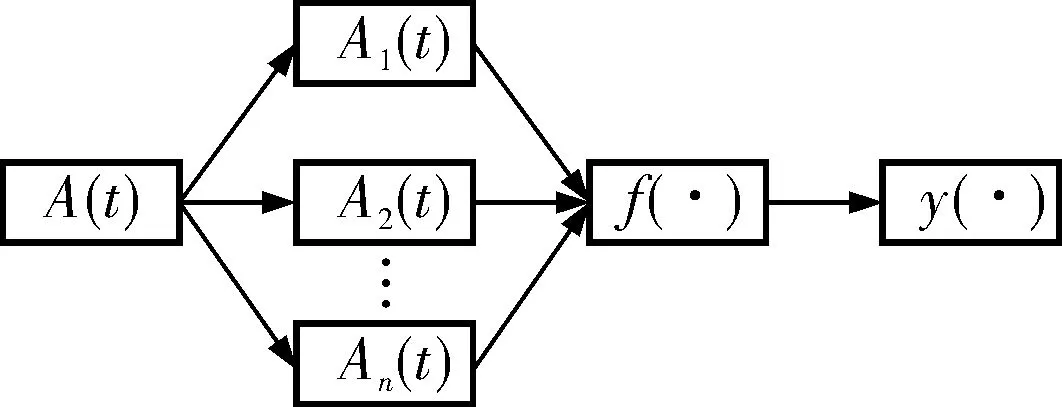
图1 动态样本多示例学习模型

图1中，A(t)为时变函数样本包，Ai(t)为包中示例，f(·)为变换函数，y(·)为输出。

时域空间的多示例学习可描述为：设某一时变函数样本包集合S={Bi(t)}，其中Bi(t)为时变函数包，每个Bi(t)具有mi个示例，记为Bi1(t),Bi2(t),…,Bimi(t)，而Bij(t)为一个时间函数向量。包Bi(t)所获得的观察结果记为f(Bi(t))，这里函数f表示某一未知的学习过程。多示例学习的目标是通过对样本集合的不断训练，最终得到未知函数映射f的一个最佳逼近F。完整的训练样例可形式化地表示为〈{Bi1(t),Bi2(t),…,Bimi(t)},f(Bi(t))〉。

1.2动态样本集的半监督学习

半监督学习的基本思想是借助数据集分布上的模型假设，通过构建机器学习模型来针对少量已标记样本和大量未标记样本进行学习与训练[13]。半监督聚类是利用样本集合中已标记样本的类别信息来辅助指导非监督聚类的过程。将数据集上的半监督学习机制进行推广，动态样本集的半监督学习问题可描述为：给定动态函数样本集S=L∪U，其中，L={(x1(t),y1),(x2(t),y2),…,(xl(t),yl)}⊂X(t)×Y是有标记样本集，Y为标签集合；U={xl+1(t),xl+2(t),…,xN(t)}⊂X(t)是未标记样本集，t∈[0,T]。半监督学习的问题是利用样本集L的标记信息，指导构建时变过程函数的学习模型，对未标记样本集U中的样本进行分析处理。

2 动态样本包间距离的度量

基于多示例表示的动态样本集合的聚类，应首先构建可度量时变函数样本包间距离的泛数，使它能够有效计算出不同样本包之间的近似度。

2.1Hausdorff距离

Hausdorff距离是一种度量数据集合之间距离的范数[14]。在多示例学习中，由于处理的对象和目标是数据包和数据包之间的广义距离关系，因此，引入一种Hausdorff距离[15]来度量包集合间的相似度：

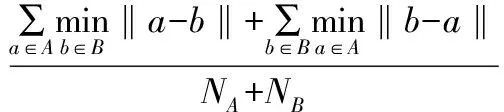
(1)

其中，a和b分别为包A和包B中的示例元素，NA和NB为集合的测度。从拓扑几何结构分析，H(A，B)为泛数空间中某一包中示例与另一包中距它最近的示例之间距离的平均值，这样定义包间的距离反映了包间示例的几何关系。

2.2时变函数样本包间的广义Hausdorff距离

基于多示例模型的动态样本聚类分析的对象为时变函数样本包，为此，将Hausdorff距离H(A,B)推广到时变函数空间，建立一种可度量时变函数样本包间性质近似度的广义Hausdorff距离。

设两个时变函数样本包分别为：

A(t)={a1(t),a2(t),…,am(t)}

B(t)={b1(t),b2(t),…,bn(t)}

其中，ai(t)=[ai,1(t),ai,2(t),…,ai,d(t)]T,bj(t)=[bj,1(t),bj,2(t),…,bj,d(t)]T,t∈[0,T],1≤i≤m,1≤j≤n,1≤k≤d。

考虑包A(t)、B(t)中的示例元素ai,k(t)、bj,k(t)，这两个函数差的2范数反映了函数间模态特征(形态、幅值等)的近似度。示例ai(t)与bj(t)之间的距离范数定义为：

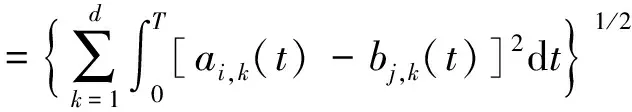
(2)

当ai，k(t)、bj，k(t)为时间区间[0,T]上的离散数据点时，采用切比雪夫范数来度量示例ai(t)与bj(t)之间的距离：

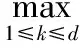
(3)

由式(1)得到多示例时变函数样本集合的一种广义Hausdorff距离：

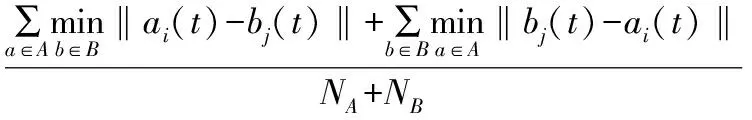
(4)

3 多示例函数样本集的半监督聚类算法

3.1设计思路

设动态函数样本包集合中的元素有K个类标签。首先，将具有相同标签的函数样本包聚合成一个聚类子集，共得到K个不相交子集，再把其他无标签样本包归类为一个子集，实现对集合的初始划分；然后，以K+1个子集的质心作为初始聚类中心点，通过设置聚类参数和距离阈值，基于广义Hausdorff距离，采用近邻传播策略[16]，对无标签样本包子集进行划分。在聚类参数控制下，即可将无标签样本归类为有标签的子集，也可生成新的聚类子集，聚类结果应满足所有样本到最近的聚类中心的相似度之和最大的原则。同时，每一步划分也要满足具有不同标签的样本包不能划分到同一子类的约束条件。在聚类过程中，考虑两种情况：样本包集合的聚类数与标签类别数相同和样本包标签类别数小于实际样本包集合的聚类数。

3.2实际聚类数与标签类别数相同时的聚类

若根据先验知识，已知集合的聚类数与样本包标签的类别数相同。在这种情况下，只需将无标签样本划分到已标记样本子集即可。

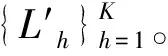
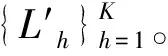
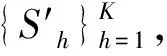
具体步骤如下：

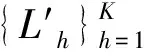
b. 从样本集U中将数据包Bi(t)(i=1,2,…,NU)加入子类Gh(h=1,2,…,K)中。

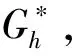
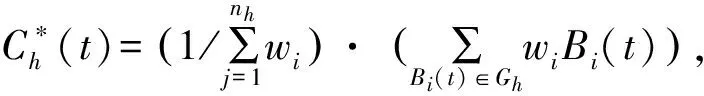
3.3样本包标签类别数小于实际样本包集合的聚类

这种情况下，设定3个聚类参数：初始聚类数目K、样本包间广义Hausdorff距离阈值θ和类间距离阈值R。在上节算法基础上，进行如下改进：

a. 将集合中非标识函数样本包依次计算与每个初始聚类中心Ci(t)之间的广义Hausdorff距离。若最小距离大于θ，则以该函数样本包作为成员形成一个新类，并以该包作为新类的聚类中心，K+1→K；否则，将该样本归于广义Hausdorff距离最小的一类，并重新计算聚类中心。

b. 计算K个聚类两两之间的类距离。若其中一个子类中所有样本均无标签，且两个类的类间距离小于R，则将这两个类合并，重新计算聚类中心；若两类类间距离大于R，则聚类不做改变；若两类中均包含有标签样本，则聚类不做改变。

c. 执行步骤a和b后，若聚类数发生改变，则以新的分类个数替代K；如果聚类结果(包括聚类数和函数样本包的具体分类)改变，则返回步骤a继续执行；如果聚类结果不再变化，则聚类完成。

在上述聚类算法中，由于广义Hausdorff距离是基于函数样本包中的示例进行距离计算的，因而突出了过程函数样本指标变量模态特征变化在聚类中的差异性。

4 在测井曲线油层水淹状况判别中的应用

测井曲线的油层水淹状况判别是油田注水开发阶段一项重要的研究工作。水淹层判别主要依据的是反映油层物理性质随深度变化的多条测井曲线的形态、幅值特征及其组合关系，水淹状况分为未水淹、弱水淹、中水淹和强水淹4个等级，一般采用自然电位SP、2.5m电阻率R25、微电极之差(Rmt-Rmd)3条测井曲线和小层厚度共4个变量进行判别。在实际中，一个油田开发区块一般只有20%的检查井进行岩心样品的取心工作，可通过实验室分析直接确定油层的水淹程度，其余的井是根据所获得的测井曲线进行人工解释来判断油层的水淹情况。如果将油层所对应的测井曲线看作是随深度变化的过程函数样本，则可利用笔者建立的多示例半监督聚类算法进行油层水淹判别。

选取某油田开发区块中23口井192个油层样本的实际测井曲线作为实验数据，每米20个采样点，其中4口检查井中37个油层样本具有水淹程度标记，覆盖了4种水淹类型。以每个油层对应的测井变量随深度变化的连续采样数据(函数)作为示例，则该示例反映了测井变量在小层上的幅值和形态特征，以4个测井变量形成的小层4维过程数据(即4个示例)构成样本包。对于取心井中的油层样本包有标签，但示例无标签；而非取心井的小层样本包和示例均无标签。在聚类过程中，以标记样本的类别代表分组类别。实际资料处理时，将不同油层样本归一化处理[17]为[0,1]区间上的函数，使每个油层对应的测井曲线具有统一的过程区间。以归一化后的SP、R25、Rmt-Rmd共3条测井曲线和油层厚度作为油层样本包中的示例。利用笔者建立的动态聚类算法对192个油层样本进行聚类分析，经过52次迭代调整后分类结果不再变化，同时满足同一聚类中不出现两种不同标记样本的约束。经与分层试油资料对比，无标签样本的正确识别率达到83.87%，这在水淹层自动判别中是一个较好的结果。

5 结束语

建立的基于多示例模型的时变函数样本集半监督聚类算法，通过构建可度量时变函数样本包间相似性的广义距离，并有效利用标记样本的先验知识和分布特征，可直接针对时域空间中的过程信号进行聚类分析，实际资料处理结果也验证了该方法的可行性和有效性。采用多示例模型，可突出指标变量模态特征的差异性，对于复杂时间信号样本的模式分类和判别问题具有较好的适应性。

[1] 汪小龙,葛运建,江剑.信息获取科学与技术中信号处理体系的研究与建立[J].信息与控制，2004,33(2)：172～176.

[2] 周治宇,陈豪.盲信号分离技术研究与算法综述[J].计算机科学，2009,36(10):16～20.

[3] Bennett K P,Demiriz A.Semi-supervised Support Vector Machines[C].Proceedings of the 1998 Conference on Advances in Neural Information Processing Systems II.Cambridge: MIT Press,1998:368～374.

[4] Decomain C,Wrobel S.Advances in Intelligent Data Analysis[M].Heidelberg：Springer,2001:309～318.

[5] Zhu X J, Ghahramani Z,Lafferty J.Semi-supervised Learning Using Gaussian Fields and Harmonic Functions[C].Proceedings of the Twentieth International Conference.Washington,DC：ICML，2003：912～919.

[6] Blum A,Chawla S.Learning from Labeled and Unlabeled Data Using Graph Min-cuts[C].Proceedings of the Eighteenth International Conference on Machine Learning. San Francisco:Morgan Kaufmann Publishers Inc,2001：19～26.

[7] Dietterich T G,Lathrop R H,Lozano-Pérez T.Solving the Multiple Instance Problem with Axis-parallel Rectangles[J].Artificial Intelligence,1997,89(12):31～71.

[8] 葛永,吴秀清,洪日昌.基于多示例学习的遥感图像检索[J].中国科学技术大学学报，2009，39(2):132～136.

[9] 李杰，程义民，葛仕明，等．基于显著点特征多示例学习的图像检索方法[J].光电子·激光，2008，19(10):1405～1409．

[10] 杨一鸣,潘嵘,潘嘉林，等.时间序列分类问题的算法比较[J].计算机学报，2007,30(8):1259～1266.

[11] Pursley M B,Royster T C.High-rate Direct-sequence Spread Spectrum with Error-control Coding[J].IEEE Trans on Commun,2006,54(9):1693～1702.

[12] 蔡自兴,李枚毅.多示例学习及其研究现状[J].控制与决策，2004，19(6)：607～610．

[13] 周志华．半督学习的协同训练算法[M].北京：清华大学出版社，2007：259～275．

[14] Edgar G A. Measure,Topology,and Fractal Geometry[M].New York:Springer,1995.

[15] 谢红薇，李晓亮．基于多示例的K-means聚类学习算法[J]．计算机工程，2009，35(22)：179～181．

[16] 肖宇,于剑.基于近邻传播算法的半监督聚类[J]．软件学报，2008，19(11)：2803～2813．

[17] 许少华,刘扬,何新贵.基于过程神经网络的水淹层自动识别系统[J].石油学报，2004，25(4):54～57.

ASemi-supervisedDynamicSampleSetClusteringAlgorithmBasedOnMulti-instanceLearning

LI Xue-gui1, XU Shao-hua1,2, LI Na3, YU Wen-tao1

(1.CollegeofComputerScience&InformationTechnology,NortheastPetroleumUniversity,Daqing163318,China;2.CollegeofInformationScienceandEngineering,ShandongUniversityofScienceandTechnology,Qingdao266590,China;3.DonghaoBranchCompany,CNPCDaqingOilfieldChemicalCo.,Ltd.,Daqing163312,China)

Aiming at the effective use of time-domain space dynamic sample’s pattern classification and mark information in time-domain space, a multi-instance learning-based semi-supervised dynamic sample clustering algorithm was proposed. Basing on both structural relationship and modal characteristics of time signals, the multi-instance information model for dynamic samples was established; through defining a generalized Hausdorff distance which measures the similarity among time-varying function samples and considering affinity propagation-based clustering principle, a semi-supervised clustering algorithm for multi-instance dynamic samples was founded. This algorithm adopts category priori knowledge to build sample set’s initially-partitioned seed cluster and to explore samples’ distribution characteristics; and it adjusts sample clustering dynamically by adopting the generalized Hausdorff distance-based affinity propagation strategy so as to highlight dynamic index modal feature’s individual difference in sample classification. Taking the recognition of oil layer’s water flooded condition in well logging as an example, both model and algorithm’s effectiveness was proved.

clustering algorithm for discriminating oil layer’s water flooded condition, time-varying function set, semi-supervised learning, multi-instance model

TP14

A

1000-3932(2016)11-1153-05

2016-09-30(修改稿)

国家自然科学基金项目(61170132)；中国石油科技创新基金项目(2010D-5006-0302)