基于CFDL_MFAC的多驱动系统协调控制的研究

郑 涛 韦晓龙

(合肥工业大学电气与自动化工程学院，合肥 230009)

基于CFDL_MFAC的多驱动系统协调控制的研究

郑 涛 韦晓龙

(合肥工业大学电气与自动化工程学院，合肥 230009)

针对多电机驱动的生产输送系统存在功率不平衡的现象，采用了一种基于紧格式动态线性化的无模型自适应控制方法来设计系统的控制器。该方法仅利用系统的I/O数据，无需对系统进行建模，就可实现对PID 3个参数的在线实时调整。经过仿真研究验证，采用笔者提出的方法，系统响应速度快、鲁棒性强、适用范围广，使电机能获得较满意的控制性能和跟随精度，控制效果优于传统PID方法。

功率平衡 动态线性化 无模型自适应控制 PID

随着煤矿生产自动化要求程度的不断提高,带式输送机要求的运量越来越大，运距越来越长，单条输送机中的装机功率也越来越大,以致在输送带张力允许的条件下采用单滚筒驱动不能提供足够的牵引力[1～3]，因此运行中大型输送机多采用双滚筒驱动。但这种方式在生产过程中若发生严重偏载,会引发烧坏电动机等其他事故[4]。因此,多机功率平衡一直被研究人员所关注[5]。为满足带式输送机功率平衡的要求，在设计之初滚筒上的功率分配就应该被确定，满足所选电机特性一致和滚筒直径偏差的严格要求。据有关文献分析,当系统的两滚筒直径偏差达到4～10mm时,运行中实际的功率分配比值与设计分配比值可相差10%～20%[6]。传统的多电机协同驱动系统功率平衡控制的研究多采用一般的PID控制器实现。PID控制器相关参数的确定需要建立被控对象的数学模型，其最大的缺点是按之前设计好的各种控制器参数对系统进行运行控制，不具备相应的在线实时调整功能[7]。而胶带机系统是一个非线性、时变的多耦合复杂系统，对控制的实时性和灵活性有着较高的要求，这就限制了传统PID控制方法的应用。

笔者将基于紧格式动态线性化无模型自适应控制[8,9](Compact Form Dynamic Linearization Based on Model Free Adaptive Control,CFDL_MFAC)与传统的增量式PID控制技术相结合，算法利用系统的I/O数据，摆脱控制系统对系统模型的过度依赖，通过对系统I/O数据的处理，结合增量式PID的模型，对所得矩阵进行逆运算，可实现对PID 3个参数的在线自整定。该算法能在线确定控制器的PID参数，速度较快，效果优于常规的增量式PID控制器。

1 多电机驱动系统功率平衡控制策略

笔者以新疆广汇白石湖露天矿区西部所用到的2.8km双电机驱动带式运输机系统为研究对象，使用所提算法对带式输送机的功率平衡问题进行研究，所选系统的简图如图1所示。其控制系统主要以PLC、变频器为核心，两台电机均在胶带机的头部。在电动机运行控制研究中，电机功率是一个间接量，不方便直接测量，在实际控制中大多选择电机的定子电流或电机的转矩代替相应的电机功率。

图1 双电机协调驱动系统

基于主从协调控制的PID控制算法在多机协调上得到了广泛的应用[10]，控制器需要控制系统的主变频器，以系统主变频器的输出电流作为其他变频器的给定电流，同时对系统所有的变频器分别实行相应的PID算法控制。对研究系统采用主从控制方式，其控制策略如图2所示，其中系统主电机M1根据预先给定的频率f1按照转速N1来运行，通过旋转编码器一对M1的运行速度进行测量，将所测速度Nc反馈给系统的控制器PLC进行PID控制运算，实现对电机M1速度的闭环控制；而对于电机M2的控制，起始频率设置与M1相同，待启动结束进入正常运行状态后，PLC通过采集得到电机M1、M2的电流I1、I2，以电流偏差e作为CFDL_MFAC算法参数自整定PID控制器的输入，控制器的输出对应于传统PID控制器的3个参数kp、ki、kd，将参数对应于某种最优控制律下得到的电流I送至变频器2，控制电机M2，最终实现系统中电机的协调运行。

图2 控制策略简图

2 基于CFDL_MFAC的控制算法

2.1CFDL_MFAC控制器的设计

笔者将基于紧格式动态线性化无模型自适应控制的PID在线自整定策略用在可控的非线性离散系统中，利用在线和离线的输入、输出数据，使算法摆脱控制器对模型的依赖，实现参数的在线自整定。该策略能简单地确定PID的3个参数，且具有快速性和抗干扰性，效果优于常规的增量式PID算法。

2.1.1问题描述

对一般的非线性SISO数学模型描述如下：

y(k+1)=f(y(k),…,(y-ny),u(k),…,u(k-nu))

(1)

假设1 系统(1)除有限的时刻点外，f(·)关于第(ny+2)个变量的偏导数是连续的。

假设2 系统(1)满足广义的Lipschitz条件，即对任意的k1≠k2，k1、k2≥0和u(k1)≠u(k2)有|y(k1+1)-y(k2+1)|≤b|u(k1)-u(k2)|,其中y(ki+1)=f(y(ki),…,y(ki-ny),u(ki),…,u(ki-nu))，i=1,2；b是一个正常数。

定理1 对满足假设1、2的非线性系统(1)，对所有时刻k有Δu(k)≠0成立时，一定存在伪偏导数φ(k)，使得系统可转换为如下CFDL数据模型：

Δy(k+1)=φ(k)Δu(k)

(2)

y(k+1)=y(k)+φ(k)Δu(k)

(3)

且|φ(k)|≤b。

2.1.2数据驱动控制算法及其收敛性分析

所设计的控制器应能使系统输出跟上期望输出，即：

y*(k+1)=y(k)+φ(k)Δu(k)

(4)

设计控制目标函数如下：

J(u(k))=[|y*(k+1)-y(k+1)2|+λ|u(k)-

u(k-1)2|]

(5)

其中，λ是一个权重因子，λ>0；y*(k+1)为期望的输出信号。

将式(4)代入式(5)中，对u(k)求偏导，并等于零，得到如下控制算法：

(6)

u(k)=u(k-1)+β[y*(k+1)-y(k)]

(7)

Δu(k)=β[y*(k+1)-y(k)]

(8)

其中，ρ是步长因子，ρ∈(0,1]；β是控制器的设计参数，β=(ρ*φ(k))/(λ+|φ(k)|2)。

由此只需要求出φ(k)，便可以求出系统的设计参数。由于φ(k)是时变参数，需要根据所选被控对象的I/O数据来求最优解：

J(φ(k))=|y(k)-y(k-1)-φ(k)Δu(k)|2+

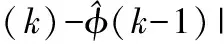
(9)

对式(9)求关于φ(k)的极值，可得：

(10)

其中η是加入的步长因子，η∈(0,1]。

适当选取λ可保证被控系统的稳定性并获取较好的输出性能，且能有效避免控制律中分母为零的情况；η、ρ使算法更具一般性，一般取值接近1可获得较好的曲线；μ是对φ(k)估计值的惩罚因子[11]。

假设3 对某一给定的有界期望输出信号y*(k+1)，总存在一个有界的u*(k)，使得系统在此控制输入信号的作用下，输出等于y*(k+1)。

假设4 对任意时刻k和Δu(k)≠0，系统伪偏导数的符号保持不变，即满足φ(k)>ε>0或φ(k)<ε<0，其中ε为一个小正数。

2.2控制器参数自整定算法

引出增量式PID的表达式：

Δu(k)=kp(k)[e(k)-e(k-1)]+ki(k)e(k)+

kd(k)[e(k)-2e(k-1)+e(k-2)]

(11)

其中kp(k)、ki(k)、kd(k)是k时刻的PID参数。令式(11)与式(8)相等，则：

kp(k)[e(k)-e(k-1)]+ki(k)e(k)+kd(k)[e(k)-

2e(k-1)+e(k-2)]=β[y*(k+1)-y(k)]

(12)

为此，假定任意3个连续的采样时刻k-2、k-1、k的PID参数固定不变，则：

kp[e(k)-e(k-1)]+kie(k)+kd[e(k)-2e(k-1)+

e(k-2)]=β[y*(k+1)-y(k)]

(13)

kp[e(k-1)-e(k-2)]+kie(k-1)+kd[e(k-1)-

2e(k-2)+e(k-3)]=β[y*(k)-y(k-1)]

(14)

kp[e(k-2)-e(k-3)]+kie(k-2)+kd[e(k-2)-

2e(k-3)+e(k-4)]=β[y*(k-1)-y(k-2)]

(15)

得到式(13)～(15)的三元一次方程组：

(16)

简写成：

A×pid=b

(17)

由此可知，式(17)中矩阵A，若rank(A)=3，则方程组必然存在唯一解pid=A-1×b，就是新的PID参数，而且使系统能够跟上期望输出；若rank(A)<3，则系统可能不存在解或者存在多解。此时不更新PID值，依旧使用上一时刻的PID值。

3 仿真实例与分析

3.1控制器参数的初始化和参数迭代的具体实现步骤

控制器参数的初始化和参数迭代的具体实现步骤如下：

b. 系统初始条件，u(1)=u(2)=0，y(1)=y(2)=0，e(k-4)=e(k-3)=0。

c. 利用式(8)、(10)，求出e(k-2)，同理求出e(k-1)和e(k)。

d. 求出矩阵A和矩阵b，若rank(A)=3，则PID参数矩阵pid=A-1×b；若rank(A)<3，则不更新PID参数矩阵。

e. 对步骤d进行迭代，更新PID控制器参数。

3.2仿真结果

笔者研究的对象是2.8km的长距离带式输送机，根据它的实际启动和运输情况来设计仿真过程。该输送机是先空载启动，其空载稳定运行的电流为20A左右。空载运行一段时间后开始向输送机装载矿石，满载的情况下，其稳定运行电流为50A左右。仿真中在20～50A过程中设了30、40A的两个过程来对该方法进行研究，模拟实际的运行情况。

设计系统的期望输出为：

其中，步长因子ρ=0.95，η=0.98；仿真权重λ=0.99，μ=0.1。

系统仿真图如图3所示，可以看出，基于CFDL_MFAC的控制策略能够在有限的时间内完成收敛，并能跟踪上系统的期望输出(误差在5%内认为跟上)，且不会出现较大的超调，能得到比较满意的控制效果。还可看出笔者方法的系统跟踪速度较增量式PID更快。该方法3个参数的变化规律如图4所示，当期望输出变化，系统的跟踪偏差较大时，PID的3个参数迅速变化，保证了跟踪曲线的快速性和平滑性；系统跟踪偏差变小时，P参数、D参数相应变化，I参数减小并趋于0；最终系统进入稳态时，PID的3个参数保持不变。由于快速性和超调是一对不可调和的矛盾，所以只能保证快速性的同时，尽量保证跟踪曲线不超调。不用通过大量工程整定试验便能得到系统的PID参数，算法和结构简单，可通过系统本身的自整定，有效地解决PID参数难以确定的缺点，并具有一定的鲁棒性。其中增量式PID的3个参数通过现场工程整定的方法设置为kp=0.7,ki=1.15,kd=0.2。

图3 笔者方法与增量式PID方法的比较仿真

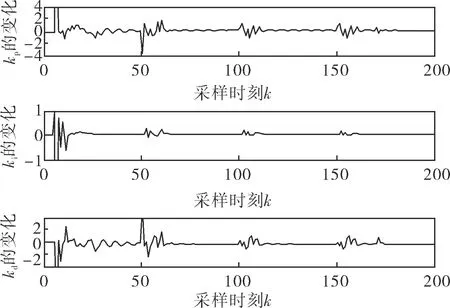
图4 自整定PID的参数变化

4 结束语

笔者采用一种基于紧格式动态线性化的无模型自适应控制来设计系统的控制器并进行系统PID参数的在线自整定。该方法的特点是相对于基于模型的控制系统而言，仅利用系统的输入输出数据，不需要对系统模型的结构和参数进行确定，就可以直接对系统的控制器进行相应的设计。通过Matlab对所提控制策略进行了仿真研究，结果表明：对于所研究系统，该方法具有快速性和抗干扰性，效果优于常规的增量式PID算法。

[1] Harrison A.Belt Conveyor Research[J].Bulk Solids Handling,2001,21(2):159～164.

[2] 张智慧.柔性螺旋输送机弹簧断裂的故障分析[J].化工机械,2009,36(5):515～516.

[3] 孟振湘,陈明杰.多装置区域协调控制的设计与实施[J].化工自动化及仪表,2001,28(6):17～22.

[4] 赵永秀,李忠,赵峻岭.煤矿双滚筒驱动带式输送机的电动机功率平衡[J].西安科技大学学报,2010,30(6):738～743.

[5] 陈梅,毛映霞,陈薇,等.基于耦合补偿的矢量变频驱动带式输送机的功率平衡控制策略[J].化工自动化及仪表,2015,42(3):241～244，281.

[6] 邓永胜,宋伟刚,赵琛.双滚筒传动带式输送机的电动机功率平衡[J].东北大学学报,2000,21(5):520～523.

[7] 陈瑞,周征.在线自校正模糊PID控制器的研究[J].自动化技术与应用,2008,27(12):49～52.

[8] 侯忠生，许建新.数据驱动控制理论及方法的回顾和展望[J].自动化学报，2009,35(6):650～667.

[9] 侯忠生.无模型自适应控制的现状与展望[J].控制理论与应用，2006,23(4)：586～592.

[10] 宋伟刚，邓永胜，郭立新.基于功率跟踪控制策略的带式输送机动态设计方法[J].东北大学学报(自然科学版),2002,23(4):899～902.

[11] 侯忠生,金尚泰.无模型自适应控制理论与应用[M].北京:科学出版社,2013.

(Continued on Page 316)

ResearchonMulti-motorCoordinationSystemBasedonCFDL_MFACControl

ZHENG Tao, WEI Xiao-long

(SchoolofElectricalEngineeringandAutomation,HefeiUniversityofTechnology,Hefei230009,China)

Considering the power imbalance in the multi-motor-driven conveying system, a model-free adaptive control method which based on compact form dynamic linearization was adopted to design system’s con-

TH865

A

1000-3932(2016)03-0236-05

2015-06-05(修改稿)