滑动平均递推PLS在芳烃异构化过程建模中的应用

陈祥华 蔡铁峰

(浙江工业大学之江学院，浙江 绍兴 312030)

滑动平均递推PLS在芳烃异构化过程建模中的应用

陈祥华 蔡铁峰

(浙江工业大学之江学院，浙江 绍兴 312030)

将滑动平滑滤波器与滑动窗递推PLS(MW-RPLS)模型结合，开发了一种滑动平均递推PLS(MA-RPLS)模型。将所开发的模型应用于芳烃异构化过程建模中。仿真结果表明：经滑动平滑滤波器去噪后的MA-RPLS模型提高了对二甲苯(PX)含量的预测精度，且各项精度指标均优于MW-RPLS模型。

MA-RPLS模型 滑动平滑滤波器 MW-RPLS模型 芳烃异构化过程 PX含量

偏最小二乘(Partial Least-Squares,PLS)是一种常用的统计回归模型，其预测精度会随着过程时变特性的变化而下降，甚至出现失效现象。为消除过程时变特性对PLS模型的影响，研究者开发了大量的递推PLS模型[1]。这些递推模型分别从预测精度[2]、跟踪性能[3]、计算负荷[4]及校正频率[5,6]等方面探讨了提高PLS模型性能的方法和策略。

当建模样本包含较大噪声时，对基于数据驱动的软测量模型的影响较大。将滑动平滑滤波器应用于去除输出变量噪声，能够降低噪声对模型精度的影响[3]；相同的方法也可应用于去除输入变量噪声[7]。基于此，笔者结合滑动窗递推PLS(MW-RPLS)模型，开发了滑动平均递推PLS(MA-RPLS)软测量模型，并以芳烃异构化过程为研究对象，估计对二甲苯(PX)含量，通过预测精度来评估所开发模型的有效性。

1 递推PLS算法①

1.1 滑动窗递推PLS算法

经标准化处理后的输入输出数据矩阵为{X,Y}，假定两者的线性关系为：

Y=XC+e

(1)

其中，C、e分别为系数矩阵和噪声向量；X∈Rn×m，Y∈Rn×l，n为样本数，m为过程变量数，l为响应变量数。

(2)

在PLS算法的基础上，基于样本均值和方差校正，研究者开发了MW-RPLS算法[3]。样本均值和方差的递推公式为：

(3)

(4)

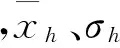
1.2滑动平均递推PLS算法

引入滑动滤波器如下：

(5)

其中，ωi为不用样本的权重，通常取ωi=1；Nk为滑动滤波器的滑动窗口长度；Ns为测试样本长度。

将该滑动滤波器与MW-RPLS算法相结合，构成MA-RPLS算法，其实施步骤如下：

a. 确定过程变量和响应变量，采集生产过程数据，并进行预处理；

b. 确定滑动滤波器的活动窗口长度Nk，运用式(5)对样本进行滤波；

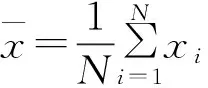
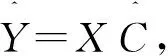
f. 判别是否收集到新的样本{X,Y}，若是则转至步骤g，否则转至步骤d；

g. 根据式(3)、(4)修正样本的均值和方差，然后转至步骤b。

2 仿真与结果分析

芳烃异构化过程的主要目标是获取更多高价值的PX[8]。经分析，可确定反应温度、氢分压、重量空速和反应器入口处各物料的质量分数为输入变量，反应器出口处PX的质量分数为输出变量。笔者将MA-RPLS模型应用于芳烃异构化过程建模的PX含量预测实验中，以验证模型的有效性。

本次实验共收集到样本600多组，将它分成两批，其中一批作为建模样本，另一批作为测试样本。MA-RPLS模型参数为：建模样本数(滑动窗口长度)90，隐含变量数7，滤波器的滑动窗口长度5。为了进行对比分析，对MW-RPLS模型也进行了同参数下的仿真实验。MA-RPLS和MW-RPLS模型的仿真结果如图1所示，可以看出，两种模型的预测值和测量值吻合度较好；滤波后，MA-RPLS模型的曲线更平滑，模型精度得到一定程度的提高。

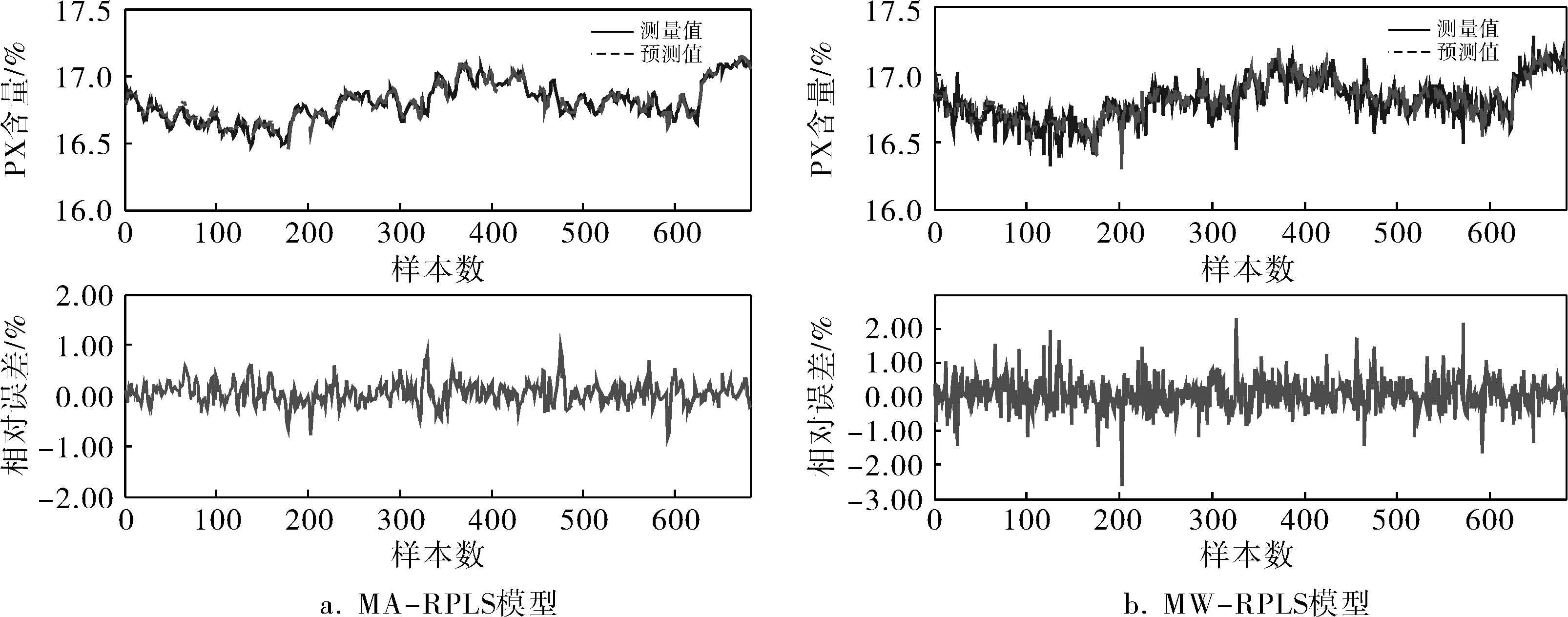
图1 仿真结果

为了进一步说明MA-RPLS模型的优越性，将两种模型的各精度指标比较结果汇总于表1。可以看出，与MW-RPLS模型相比，经滑动平滑滤波器处理后的MA-RPLS模型的各精度指标大幅下降，说明变量噪声对模型精度的影响程度变小，变量噪声处理具有一定的必要性和重要性。

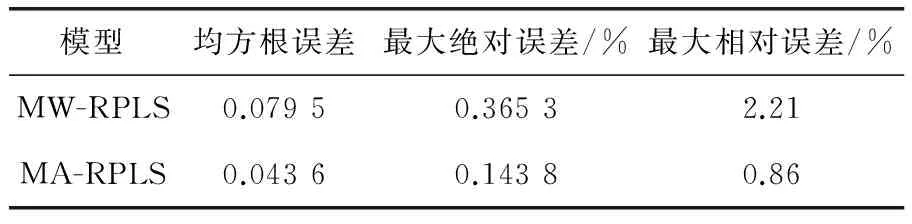
表1 两种模型的性能比较

3 结束语

笔者基于MW-RPLS模型，结合滑动平滑滤波器，开发了一种MA-RPLS模型，并将它应用于芳烃异构化过程PX含量估计中。仿真结果表明：由于MA-RPLS模型考虑了过程数据的噪声，因此相比于MW-RPLS模型，MA-RPLS模型的预测精度得以大幅改善，模型性能有了大幅提高，具有一定的优越性。

[1] Helland K,Berntsen H E,Borgen O S,et al.Recursive Algorithm for Partial Least Squares Regression[J].Chemometrics and Intelligent Laboratory Systems,1992,14(1):129～137.

[2] Qin S J.Recursive PLS Algorithms for Adaptive Data Modeling[J].Computers and Chemical Engineering,1998,22(4-5): 503～514.

[3] Mu S,Zeng Y,Liu R,et al.Online Dual Updating with Recursive PLS Model and Its Application in Predicting Crystal Size of Purified Terephthalic Acid(PTA) Process[J].Journal of Process Control,2009,16(6):557～566.

[4] Liu J L,Chen D S,Shen J F.Development of Self-Validating Soft Sensors Using Fast Moving Window Partial Least Squares[J].Industrial and Engineering Chemistry Research,2010,49(22):11530～11546.

[5] Lee Y H,Kim M,Chu Y H,et al.Adaptive Multivariate Regression Modeling Based on Model Performance Assessment[J]. Chemometrics and Intelligent Laboratory Systems,2005,78(1):63～73.

[6] 徐欧官,陈祥华,傅永峰,等.基于模型性能评估的递推PLS建模及应用[J].化工学报,2014,65(12):4875～4882.

[7] Facco P,Doplicher F,Bezzo F,et al.Moving Average PLS Soft Sensor for Online Product Quality Estimation in an Industrial Batch Polymerization Process[J].Journal of Process Control,2009,19(3):520～529.

[8] 徐欧官,陈祥华.移动窗递推PLS软测量建模及其工业应用[J].高校化学工程学报,2009,23(6):1044～1050.

ApplicationofMovingAverageRecursivePLSModelinAromaticsIsomerizationProcess

CHEN Xiang-hua, CAI Tie-feng

(ZhijiangCollege,ZhejiangUniversityofTechnology,Shaoxing312030,China)

A moving smooth filter was incorporated into the moving window recursive PLS (MW-RPLS) model to develop a moving average recursive PLS (MA-RPLS) model for aromatics isomerization process. The simulation results show that, the PLS (MA-RPLS) model denoised by the moving smooth filter can improve the accuracy of predicting p-xylene content and its data of accuracy outperforms that of the MW-RPLS model.

MA-RPLS, moving smooth filter, MW-RPLS model, aromatics isomerization process, p-xylene content

TH865

A

1000-3932(2016)12-1299-03

2016-07-14(修改稿)

国家自然科学基金项目(61203133，61304125)