高职教育对广东省经济增长率的贡献研究
彭丽花
(广东开放大学,广东 广州 510091)
高职教育对广东省经济增长率的贡献研究
彭丽花
(广东开放大学,广东 广州510091)
本文以柯布-道格拉斯生产函数为基准模型,估算得到广东省的劳动产出弹性为0.6,低于国际上通用的麦迪逊系数0.7,说明我国广东地区的劳动力产出弹性不具备国际竞争力。最后根据教育综合指数法,对广东省2001-2013年的有关数据进行测算,得到高职教育对广东省经济增长率的贡献为0.49%,比本科教育的贡献率低0.2%。得出结论:教育层次越高,教育发展指数增长越快,对经济的贡献率也越大。
高职教育;教育综合指数;经济增长率;贡献
高职教育服务于区域经济,一般而言,经济发达的地方,高职教育也相对比较发达。广东省作为经济大省,高职教育的发展也走在全国前列。2006年教育部颁布了 《关于全面提高高等职业教育教学质量的若干意见》(教高〔2006〕16号),明确了高等职业教育是高等教育的一个类型,给予高职教育正本清源的重要地位,也迎来了高职教育的稳健发展阶段。广东省高职教育起步于上世纪80年代,高职院校数量从17所发展到现在的79所,招生数和在校生数规模逐年上升,占比在2003年达到最高点,分别占全省普通高校招生数、在校生数的比例为59.66%、52.76%。可见,高职教育已经占据了高等教育的半壁江山,为地区经济培养了大量的高素质技能型人才。本文拟测度高职教育对广东省经济的贡献到底有多大,这对于处理好广东省教育与经济的关系具有重要意义。
一、估算方法介绍
衡量教育对经济贡献的定量方法有很多,在西方,无论是舒尔茨的余值分析法,还是丹尼森的经济增长因素分析法,都是以柯布-道格拉斯生产函数为基准模型,依据罗默的内生化经济增长理论,将人力资本(包括教育投入)视为内生变量,与资本和劳动力一起纳入经济增长模型。国内学者崔玉平认为教育对经济的作用主要是通过提高劳动力的素质进而提高劳动生产率实现的,它的作用相当于使未受正规教育的初始劳动力(或基准劳动力)的数量成倍增加。[1]本文基于上述思路构建经济增长模型。
在此,简单介绍一下柯布-道格拉斯生产函数。依赖于时间t的动态生产函数为:Yt=Atf(Kt,Lt)=AtKtαLtβ(式1)。为便于分析,假定各个时期的技术水平保持不断,其中A代表技术水平,Kt代表各期物资投入,Lt代表劳动投入。根据崔玉平的观点,Lt=L0t*Et(式2),L0t代表各期的初期劳动力,Et代表教育投入。将式2代入式1中,得到Yt=AKtαL0tβEtβ(式3)。对式3的两边同时取对数,对时间t求导,得出经济增长率模型:y=a+αk+βl0+ βe(式4)。这里,y代表经济年增长率,α代表资本投入的产出弹性,k代表资本投入的年增长率,β代表劳动力的产出弹性,l0代表初始劳动投入的年增长率,e代表教育的年增长率,其中α+β=1。那么,可以计算出教育对经济的贡献率为Re=βe/y。由此可以看出,只需估算出β、e与y值,就可以得到教育对经济的贡献率。要想计算出高职教育对经济增长率的贡献,还需要进一步计算出高职教育指数增长率占教育综合指数增长率的百分比W1,即可得到其对经济增长的贡献率R1= W1*Re。
二、β系数值的估计
α、β值在不同国家不同时期是不确定的,国内学者在进行分析时方法也不一。杭永宝(2007年)为了增加计算结果的国际可比性,采用麦迪逊的β系数值,即β=0.7。[2]程兰芳等(2008年)则采用了时间序列法,即在C-D生产函数的基础上,通过构造回归模型lnYt= lnA+αlnKt+βlnLt+μt,分别估算出α和β的数值。[3]本文采用后一种办法,通过选取1998年至2013年广东省的有关数据,其中国内生产总值GDP代表Y、固定资产投资代表K、从业人员数代表L。为了剔除物价的影响,以1998年作为基期,将固定资产投资和GDP均进行平减。
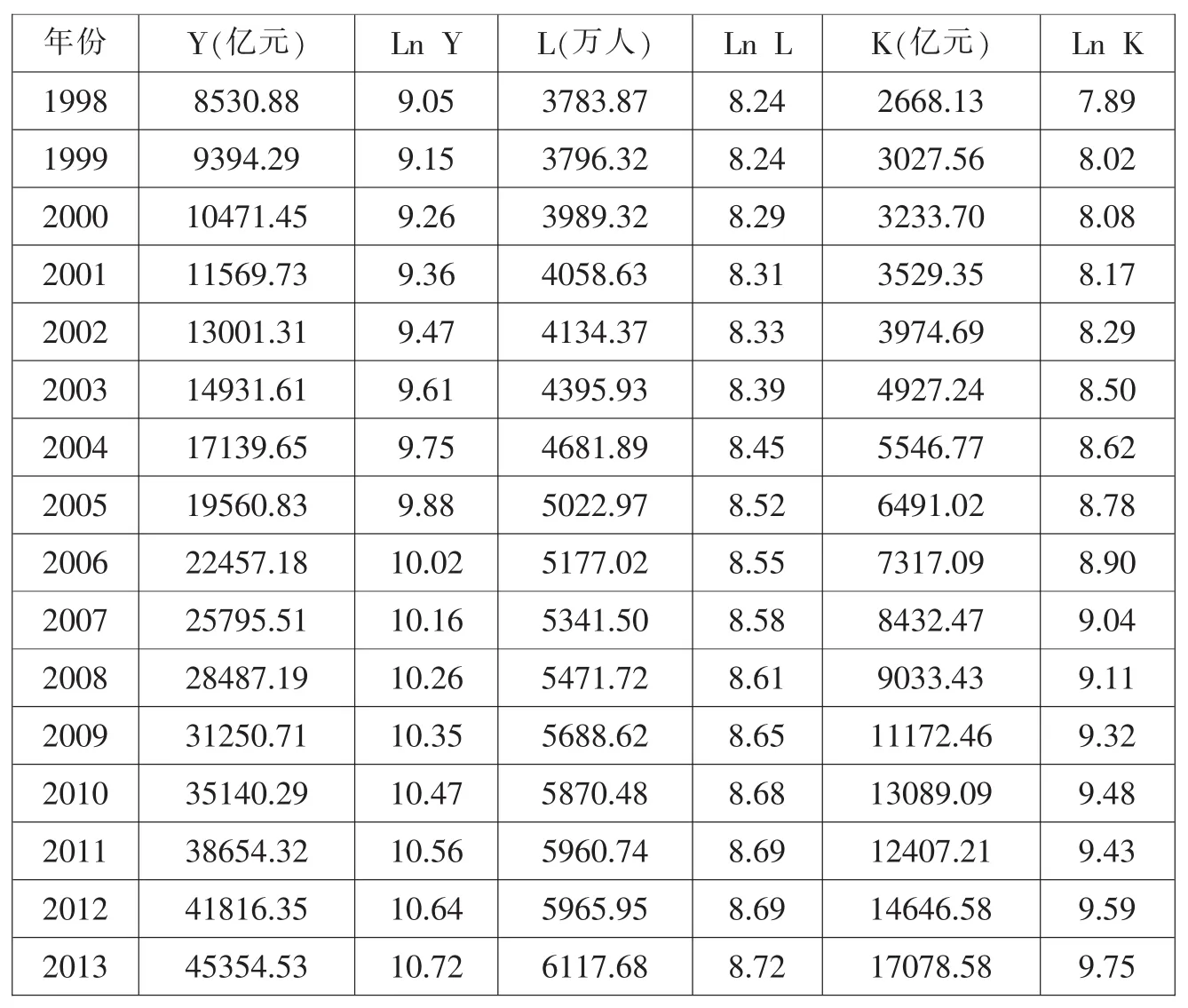
表1 广东省1998-2013年国内生产总值、固定资产投资、从业人员投入模型数据

表2 EVIEWS6.1运行结果
根据表1中的数据,采用软件EVIEWS6.1进行OLS回归,输出结果如表2所示。
得到的回归方程如下:lnYt=lnA+0.64lnKt+0.96lnLt+ μt。
(1)回归系数的显著性检验(即t检验)。在给定显著水平0.05下,方程中的LnK和LnL的t统计值分别为t1=5.489499、t2=2.363850均大于t0.05/2(13)=2.16037。说明回归系数均通过显著性检验。
(2)拟合优度检验。根据运行结果,可知R2=0.996247, R2的修正值=0.995669,无论哪个值均接近1,说明方程的拟合优度很好,回归线对各样本点的拟合程度很高。
(3)方程的显著性检验(即F检验)。F0.05(2,13)=3.8,运行结果中的F=1725.321>F0.05(2,13),F检验通过验证,表明在95%的概率水平下固定资产投入、劳动力投入对国内生产总值的影响具有显著性。
综上所述,回归方程均能通过各项检验,模型估算得到的α= 0.64,β=0.96。经过归一化处理,αˆ= 0.4,βˆ=0.6。比麦迪逊估计β值为0.7略低,这也验证了杭永宝的观点:实际上,我国的β值可能低于0.7[2]。结果表明在我国的广东省地区劳动力的产出弹性不具备国际竞争力,意味着即在其他条件不变的情况下,劳动每增加1%,产出将增加0.6%;资本每增加1%,产出增加0.4%。
三、测算高职教育对广东省经济的贡献率
由于《中国劳动统计年鉴》中未对2000年从业人员各文化程度分布的百分比进行统计,所以本文分析的时间节点是2001年至2013年。同时,为了研究的方便,将研究生及以上教育一并合到本科教育进行分析。根据上文构建的经济增长模型及回归运算得到的β值,可将高职教育对广东省经济增长率贡献的计算过程沿着以下思路展开。
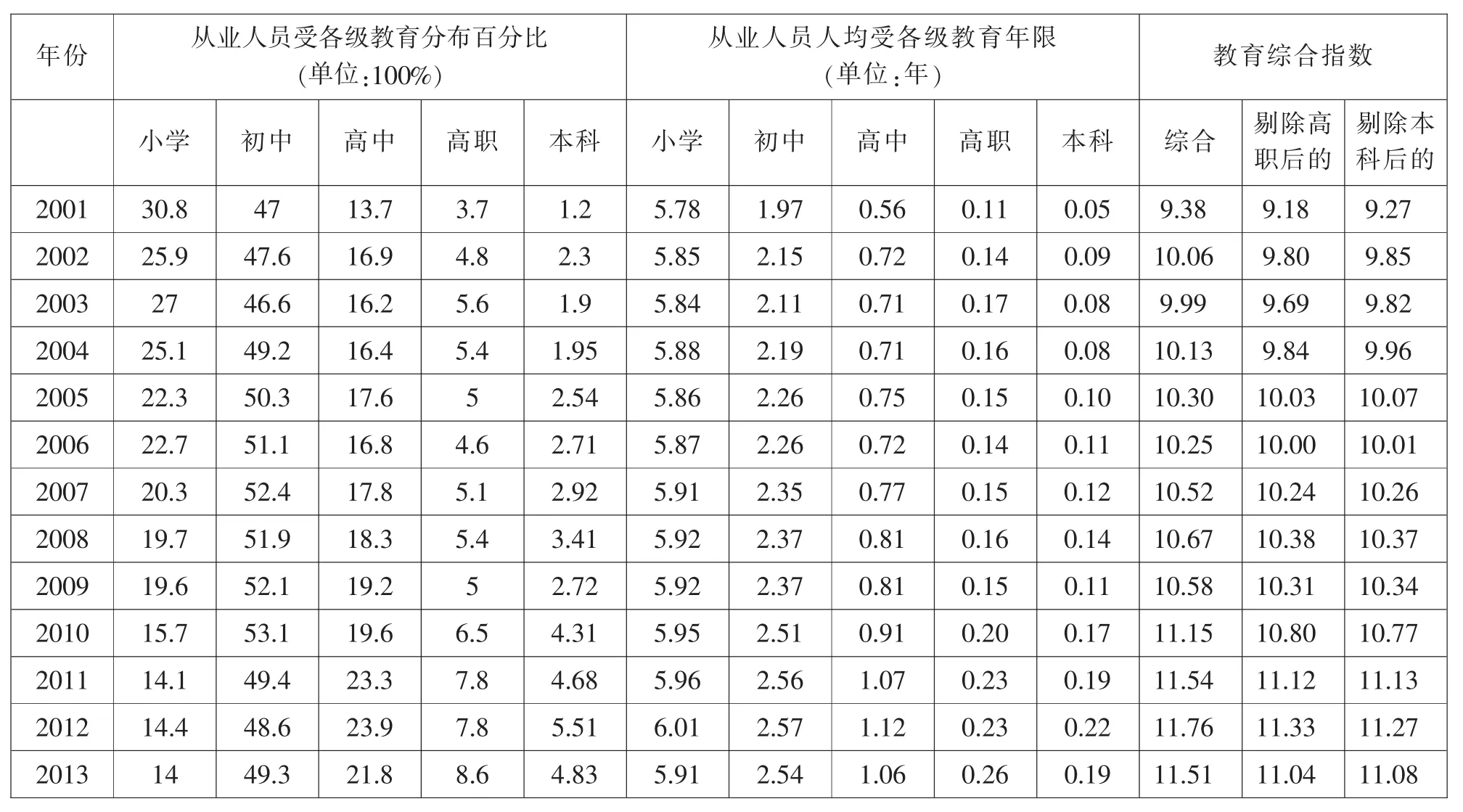
表3 广东省2001-2013年从业人员人均受各级教育的情况
(一)选择合适的劳动力质量换算为劳动力数量的系数
不同教育程度的劳动者,劳动生产率不同。在李实(2003)展开的《对中国城镇教育收益率的长期变动趋势》一文的研究中,根据中国社会科学院经济研究所在2000年开展的住户抽样调研中,受小学、初中、普通高中、高职、本科教育从业人员的平均收入比为1∶1.28∶1.38∶1.81∶2.20。[4]据此,可以将2001年接受小学、初中、普通高中、高职、本科教育的劳动力折算系数确定为:1、1.28、1.38、1.81、2.20。
(二)计算各年从业人员人均受各级教育年限、教育综合指数
根据《中国劳动统计年鉴》可以查询到小学、初中、高中、高职、本科文化程度的从业人员占总就业人数的百分比,见表3第1部分。根据我国目前教育所实行的学制,小学、初中、高中(含中专)、高职、本科教育的受教育年限分别为6年、3年、3年、3年、4年。按照下列公式可以计算出从业人员人均受各级教育年限:Hi= Ni*∑fi*100%(式5),其中,i代表各级教育,Hi为从业人员人均受教育年限,Ni为各级教育年限,fi为从业人员受本级及以上教育的比重之和。根据广东省从业人员人均受各级教育年限(表3的第2部分),我们可以依据公式 Ei=1*H1i+1.28*H2i+1.38*H3i+1.81*H4i+ 2.20*H5i计算得到教育综合指数,结果见表3的第3部分。教育综合指数代表由于教育程度提高而带来的劳动投入量。[5]
(三)计算教育综合指数年均增长率、剔除高职后的教育综合指数年均增长率、剔除本科后的教育综合指数年均增长率
根据公式e=(Ei/Ei-1)-1(i=2,3……13)(式6),可以得到各年间教育综合指数增长率。取算术平均值,可以得到2001-2013年间的平均教育综合指数的增长率。由于前文在区分不同劳动者的劳动生产率差异时,主要是依据工资的不同,而个人的天赋、家庭背景、勤奋努力程度等均会造成个人收入的不同,只有一部分是可以归因于教育因素,因此根据丹尼森等学者通行的算法,对于依据工资差别而计算出的教育综合指数的增长率用0.6做折算[1],因此折算后的教育综合指数年均增长率为e*=0.6*e=1.05%。
同样地,可以得到剔除高职教育后的教育综合指数年均增长率e1=0.95%、剔除本科以上教育后的教育综合指数年均增长率e2=0.91%。
(四)分别计算高职教育指数增长率占教育综合指数增长率的百分比、本科教育指数增长率占教育综合指数增长率的百分比
高职教育指数增长率占教育综合指数增长率的比重为W1=(e*-e1)/e*=(1.05%-0.95%)/1.05%=9.52%,本科教育指数增长率占教育综合指数增长率的比重为W2=(e*-e2)/e*=(1.05%-0.91%)/1.05%=13.33%。
(五)计算实际经济年均增长率y
以上一年为基期,根据GDP指数,可以计算得到各年的实际经济增长率。经算术平均,得到y=12.25%。
(六)分别计算教育、高职教育、本科教育对经济增长率的贡献
有了教育综合指数年均增长率e、实际经济年均增长率y和β,可以得到教育对经济增长率的贡献为Re=β*e/y=0.6*1.05%/12.25%=5.14%。高职教育对经济增长率的贡献为R1=W1*Re=9.52%*5.14%=0.49%,本科教育对经济增长率的贡献为 R2=W2*Re=13.33% *5.14%=0.69%。
四、结果分析
由上面的分析可知,在广东经济12.25%的增长速度中,有0.63是教育所带来的,所占的份额为5.14%,即教育对广东省经济增长率的贡献为5.14%,其中高职教育的贡献为0.49%、本科及以上教育的贡献为0.69%。可见,高职教育对广东省经济增长的贡献率是非常低的,比本科教育低0.2个百分点。两者相加得到高等教育对广东省经济的贡献率为1.18%,这个水平大体上只相当于1950年美国的(1.29%)、日本的(1.05%)[1],可见与发达国家相比存在着很大的差距。
高职教育贡献率偏低这种情况在我国具有普遍性。国内学者在研究高职教育对区域经济的贡献率时大都采用的是教育综合指数法,尽管选择的劳动产出弹性系数和劳动简化系数不一,但是国内高职教育的经济贡献率大都不超过1%。李中国的研究认为2001-2012年间全国、东部、中部、西部高职对经济的贡献率分别为0.64%、0.78%、0.57%、0.55%[6],张宏霞测算出2003-2011年间大连市高等职业教育对经济增长的贡献率为0.14%[5],孙丽测算出2001-2010年间高职教育对浙江经济增长的贡献率为0.75%[7]。
究其原因,笔者认为有三:第一,现阶段高职教育整体规模偏小。2013年广东省从业人员中受高职教育的比例为8.6%,从业人员人均受高职教育年限仅为0.26年。第二,高职教育经费投入的不足。随着高校扩招,我国普通高校生均经费面临持续下降的趋势。结果反映在扩招的首年,教育综合指数开始下降,由10.06降至9.99。第三,高职院校专业设置结构与区域经济产业结构的不匹配,导致培养出来的人才无法直接转化为当地的生产力。
五、结论及建议
经测算可以得到各年间各类教育指数的增长率,如图1所示,进而可以得到2001-2013年间各级教育指数年均增长率分别为0.19%、2.19%、5.85%、8.24%、14.72%。本科教育指数增速最大,高职教育其次。因此可以推断,教育层次越高,教育指数增速越快,其对经济增长率的贡献越大。
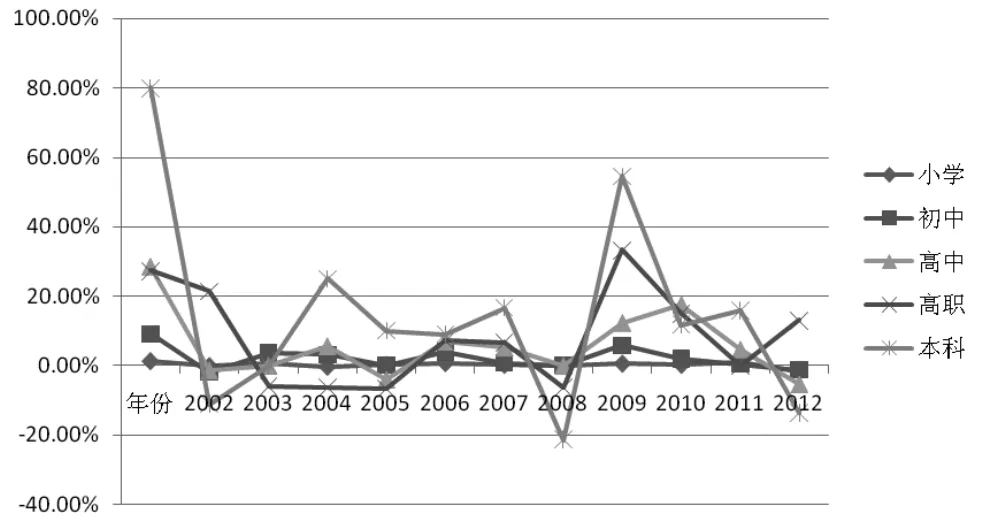
图1 各年间各类教育发展指数的增长率
当务之急,要提高高职教育对经济的贡献率,关键在于要提高从业人员人均受高职教育年限,从而提高高职教育指数增速。首先,要加大经费投入,提高高职生均经费,推进高职院校的课程建设,改善实践教学条件。这也刚好印证了前文的分析:广东省的资本和劳动的产出弹性之和大于1,说明经济规模处于收益递增的态势。其次,高职院校要明白自己的“地域性、职业性”的办学优势,与本科院校在专业设置上错位发展,根据区域经济发展需要开设专业,创新人才培养模式,明确人才培养目标,才能有效地推动区域经济的发展。
[1]崔玉平.中国高等教育对经济增长率的贡献[J].北京师范大学学报,2000,(1).
[2]杭永宝.中国教育对经济增长贡献率分类测算及其相关分析[J].教育研究,2007,(2).
[3]程兰芳,王园园.北京市高等教育对经济增长贡献的计量分析[J].辽宁教育研究,2008,(9).
[4]李实,丁赛.对中国城镇教育收益率的长期变动趋势[J].中国社会科学,2003,(6).
[5]张宏霞.大连市高等职业教育对经济增长贡献率的实证分析[J].邢台职业技术学院学报,2014,(4).
[6]李中国,郭艳梅,李玲.西部高职教育对经济增长贡献率的实证分析与政策建议[J].国家教育行政学院学报,2015,(5).
[7]孙丽.高等职业教育对欠发达地区经济发展贡献的实证研究——以衢州地区为例[J].北方经济,2012,(9).
G459
A
1671-2862(2016)01-0084-04
2015-08-23
本文系广东开放大学校内科研课题“高职教育与区域经济发展的相关性研究——以广东省为例”(课题编号:1317)的研究成果。
彭丽花,女,湖南衡阳人,硕士,广东开放大学讲师,研究方向:物业管理、区域经济学。

