微型压电振动发电机谐振频率调节技术的研究*

闫　震，何　青，王东平，刘俊峰

（1.河北农业大学机电工程学院，河北保定071001；2.华北电力大学能源动力与机械工程学院，北京102206；3.河北农业大学现代科技学院，河北保定071001）

微型压电振动发电机谐振频率调节技术的研究*

闫震1*，何青2，王东平3，刘俊峰1

（1.河北农业大学机电工程学院，河北保定071001；2.华北电力大学能源动力与机械工程学院，北京102206；3.河北农业大学现代科技学院，河北保定071001）

具有高能量密度的微型压电振动发电机可以无限、持续地为无线传感器网络提供能量。为了适应环境振源频率的变化，提高压电振动发电机的能量转换效率，采用理论建模和数值分析的方法，研究了旁路电容调节振动发电机固有频率的关键技术。建立压电电容与压电层杨氏模量的力学模型，分析压电电容对压电发电机固有频率的影响规律，提出了单晶片和双晶片压电梁的电容频率调节配置方案；分别研究厚度比、长度和宽度对开路、闭路刚度比及固有频率比的影响特性，对结构参数进行了优化配置。

无线传感器网络；压电式振动发电机；旁路电容；固有频率

应用微机电加工技术制造的悬臂梁压电式振动发电机可以无限、持续地为各种低功耗电子器件提供能量，有效地解决了无线传感器网络在苛刻工作环境中能源供给难题［1-9］。然而，悬臂梁压电振动发电机对环境振源频率的变化很敏感，若环境频率偏离压电发电机固有频率2 Hz～3 Hz，将导致输出功率急剧下降。为了提高悬臂梁压电振动发电机的环境适应能力，通常采用附加外部机械装置来改变悬臂梁的结构或刚度，以调节其固有频率。但是，该方法增大了压电发电机体积和制作难度，也提高了生产成本。针对上述问题，本文采用旁路电容调节压电梁的固有频率，以适应振源环境的变化，通过分析压电梁的结构参数对旁路电容频率调节范围的影响规律，提出了结构参数优化配置方案，为提高有限体积悬臂梁压电式振动发电机的发电能力，奠定了研究基础。

1　旁路电容频率调节理论建模

悬臂梁压电发电机固有频率公式

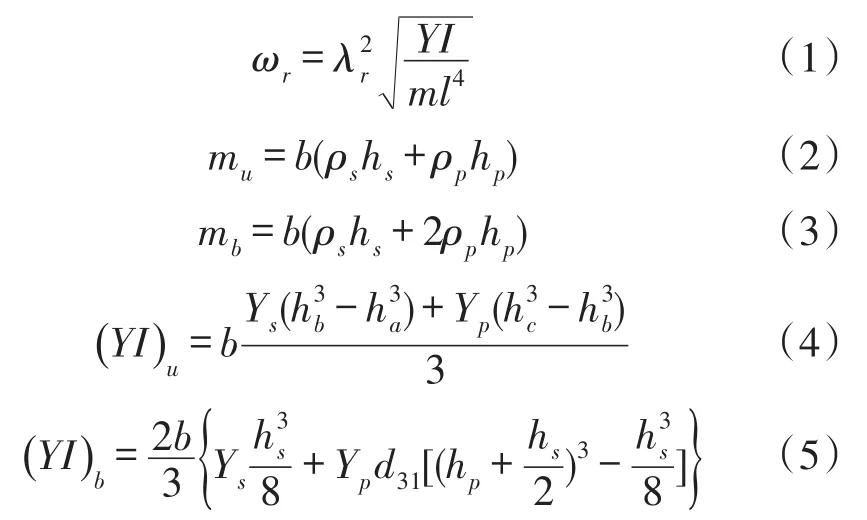
悬臂梁压电发电机的固有频率［10］为

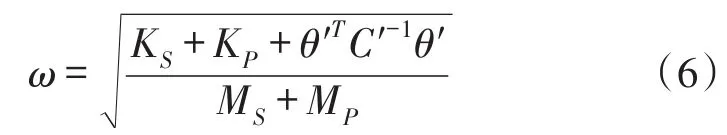
式中，MS和MP分别为基板和压电层的质量矩阵，KS和KP分别为基板和压电层的刚度矩阵，C′是压电电容矩阵，θ′是压电机电耦合矩阵，KP+θ′TC′-1θ′为压电层的等效刚度。压电梁总等效刚度由基板机械刚度KS、压电层机械刚度KP和机电耦合刚度θ′TC′-1θ′构成，其等效连接方式如图1所示。

图1　悬臂梁压电发电机等效刚度

由式（6）可知，通过改变压电层的机电耦合项或电容值，可以改变系统刚度，进而实现固有频率的调节。但是，机电耦合项由压电层材料特性和复合梁的几何形状决定，一般不易改变，因而只能通过改变压电电容值来调节固有频率。据此，设计在压电层并联旁路电容，通过调节系统的压电电容值改变固有频率。其原理为：系统总电容为旁路电容与压电电容之和；当旁路电容短路CS=∞时，机电耦合刚度项θ′T（C′+CS）-1θ′=0，压电梁等效刚度最小，固有频率最低；随着旁路电容值逐渐降低，机电耦合刚度项θ′T（C′+CS）-1θ′随之升高，当降低到旁路电容开路状态CS=0时，机电耦合刚度项达到最大值，等效刚度和固有频率值最高，如图2所示。

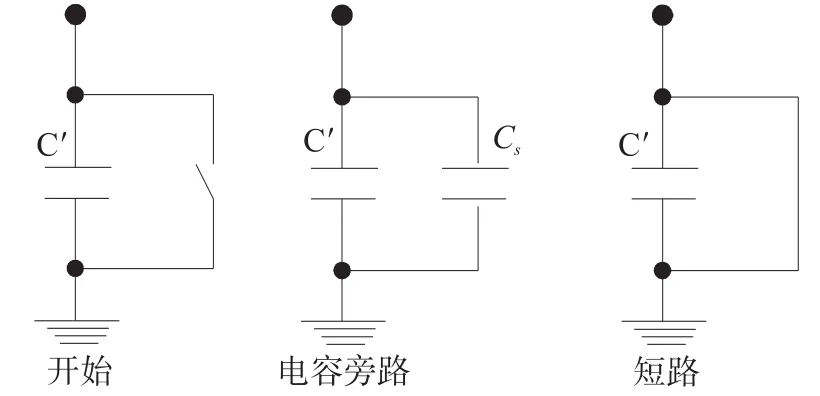
图2　旁路电容频率调节方式

由上述分析可知，旁路电容短路和开路状态分别为固有频率调节范围的下极限和上极限状态；压电调节层的开路固有频率与短路固有频率之比，决定了压电梁的谐振频率调节范围。

为了分析不同压电梁结构对电容频率调节范围的影响，将双晶片压电梁的两个压电层分为能量收集层hp和频率调节层ht，各压电层具有独立的收集和调节作用，通过改变各层的位置和厚度，分析其对刚度及固有频率的影响，如图3所示。为便于表述，将图3（a）、图3（b）和图3（c）中的双晶片压电梁结构分别称为双晶片压电梁A、双晶片压电梁B和双晶片压电梁C。

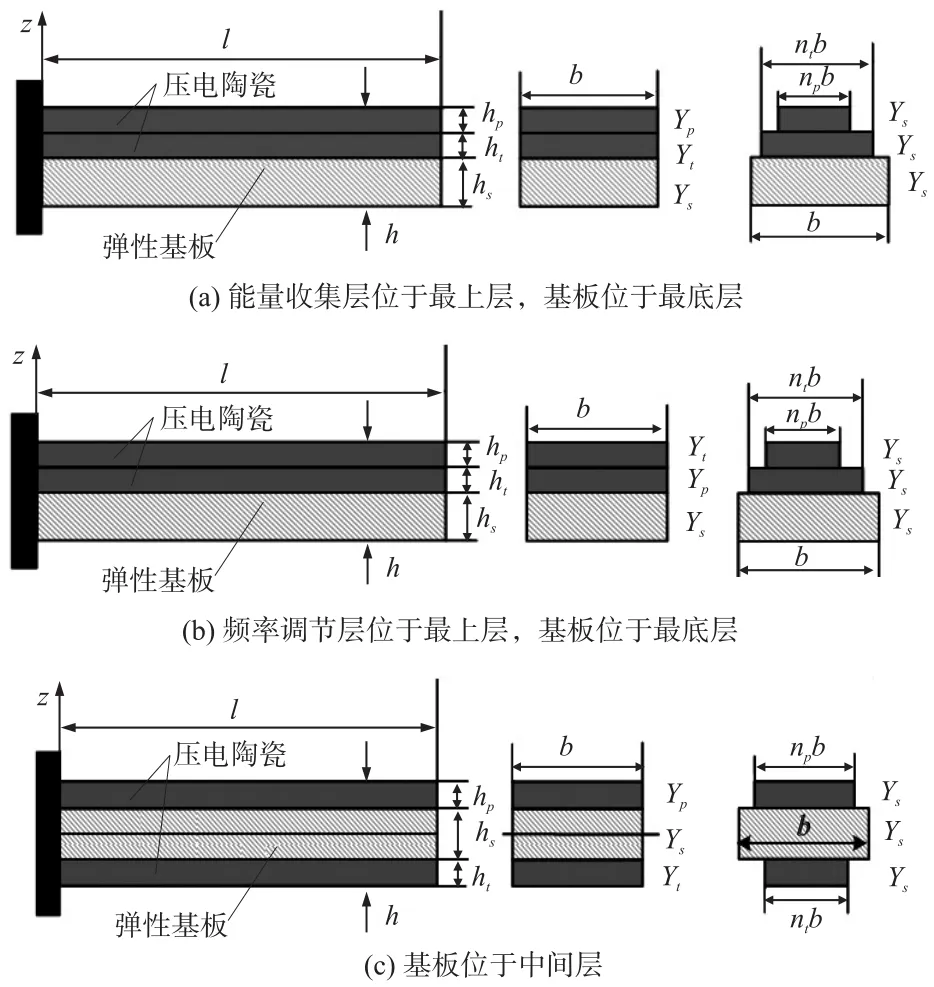
图3　收集层、调节层和基板具有不同相对位置的双晶片压电梁结构图

由于压电和基板材料具有不同的弹性模量和密度，因此，在计算惯性矩前，必须对横截面宽度进行转换，将两层材料以同一弹性模量表示，以确定复合梁横截面中性轴的位置。据此，令基板作为转换后的单一材料，定义弹性模量比［11］

由于基板材料的弹性模量大于压电陶瓷的弹性模量，由式（7）可知，np和nt均小于1，因此，转换后基板宽度b大于压电层宽度npb和ntb。

在图3（a）中，压电梁的中性轴位置为

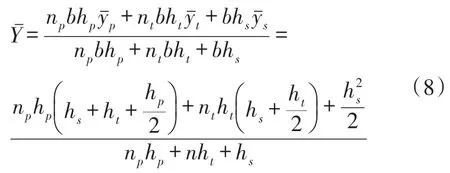
式中，复合梁各层的中性轴高度y¯i以梁的底部为基线。

惯性矩为

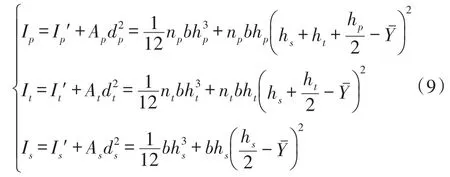
在图3（b）中，梁的中性轴位置

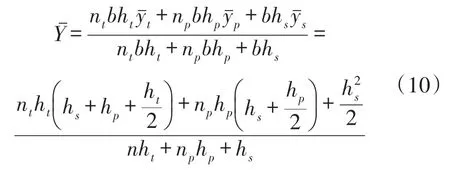
惯性矩为

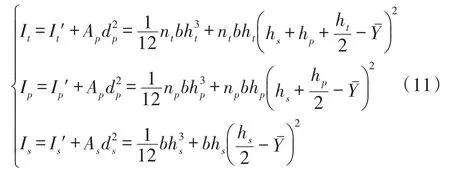
在图3（c）中，梁的中性轴位置

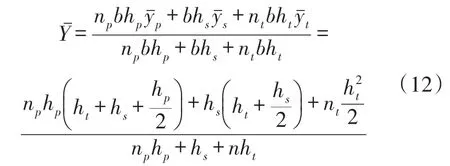
惯性矩为

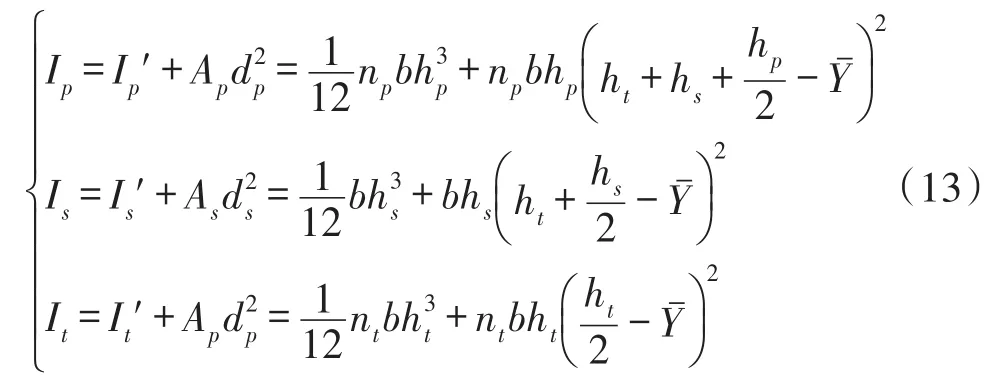
式中，As为基板的横截面面积，Ap为压电层的横截面面积，ds为基板中性轴与复合材料中性轴的距离，dp为压电层中性轴与复合材料中性轴的距离。

图3中双晶片压电梁的弯曲刚度为

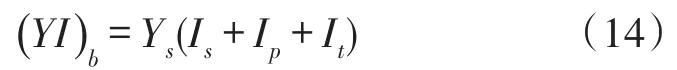
压电调节层的弹性模量为［12］

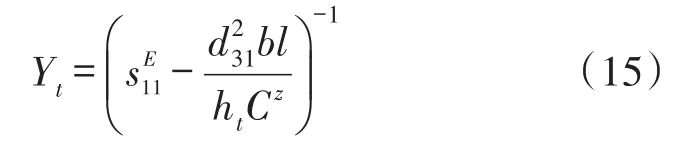
式中，Cz为压电电容Ct与并联电容Cs之和。

当调节层为短路状态时，旁路电容Cs=∞，因此Cz=∞，压电调节层的弹性模量与柔顺系数成反比

当压电调节层为开路状态时，则旁路电容Cs值为0，调节层的弹性模量为

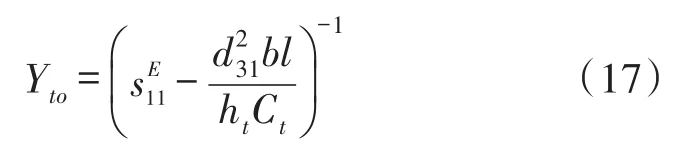
由于压电电容

因此，式（17）可写为

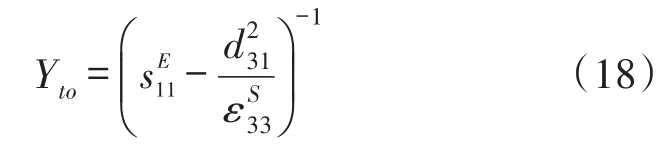
由式（16）和式（18）可知，悬臂梁压电发电机开路时的杨氏模量要大于短路时的杨氏模量。

上述分析表明，通过改变压电调节层的旁路电容，能够有效改变悬臂梁压电发电机的弹性模量，从而使有效刚度发生变化，实现对固有频率的调节。

2　旁路电容频率调节数值分析

以表1中的单晶片压电梁参数作为计算数据，双晶片压电梁参数与单晶片压电梁相同，仅压电层厚度为单晶片压电梁压电层厚度的1/2，研究旁路电容对固有频率的影响规律，分析尺寸及材料参数与旁路电容频率调节范围的关系。由于旁路电容频率调节方式通过改变压电梁刚度来调节固有频率，且开路和闭路固有频率比决定频率调节范围，因此，本节通过式（18）、式（16）、式（14）和式（1）计算开路、短路刚度和固有频率，分别研究厚度比、长度、宽度和材料参数对开路、短路刚度比及固有频率比的影响规律，以压电梁的固有频率调节范围和能量收集最大化为目标，优化结构尺寸和材料参数。

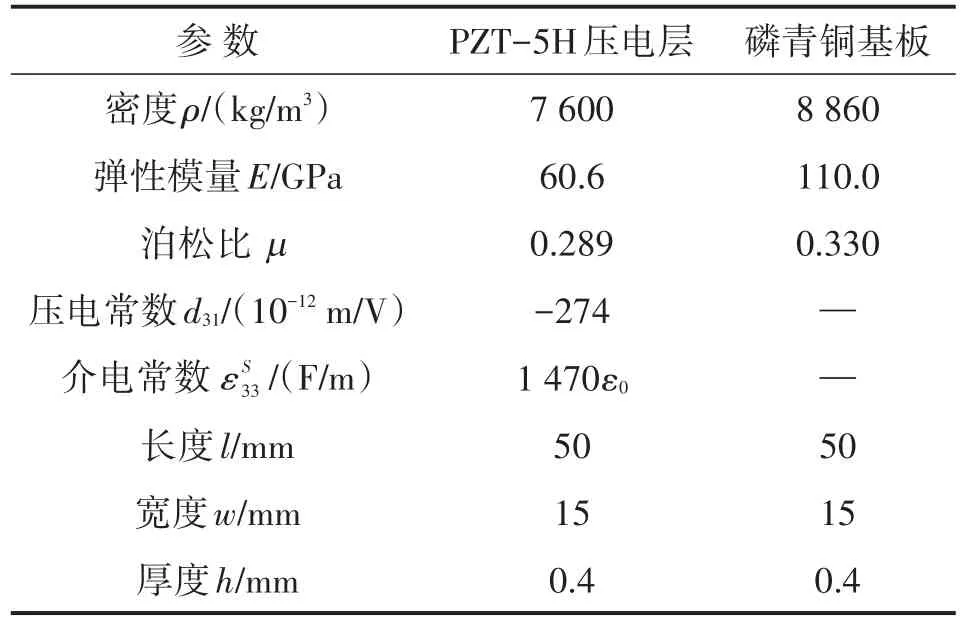
表1　单晶片压电梁结构和材料参数

2.1旁路电容频率调节特征

为了研究旁路电容对频率调节范围的影响规律，分析压电梁固有频率与短路固有频率比随旁路电容与压电电容比的变化规律。结果表明，随着旁路电容值的增加，压电梁的固有频率逐渐降低；连续调节旁路电容，可以得到开路频率和闭路频率间的任意频率。同时还发现，单晶片和双晶片压电梁的旁路电容频率调节规律基本一致，仅范围不同，当0＜Cs/Cp＜5时，固有频率变化较为明显；当Cs/Cp＞10时，改变旁路电容值，压电梁的固有频率基本不会变化；双晶片压电梁C两压电层同时调节时，频率调节范围最大，而双晶片压电梁B频率调节范围较窄，如图4所示。

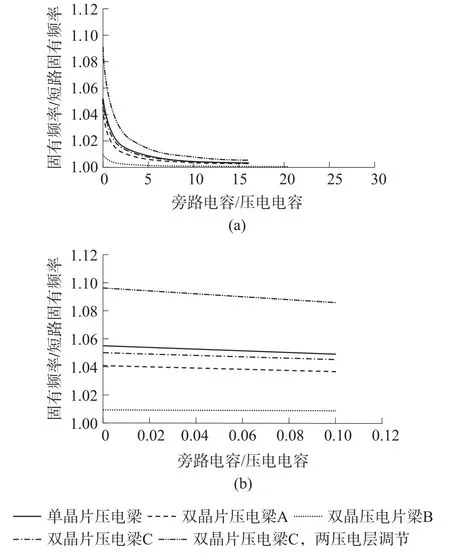
图4　固有频率比与电容比的关系

2.2厚度比对旁路电容频率调节范围的影响

压电层厚度固定不动，仅改变基板厚度，研究单晶片压电梁的开路、短路刚度比和固有频率比随基板厚度与压电层厚度比的变化规律。研究结果如图5所示。

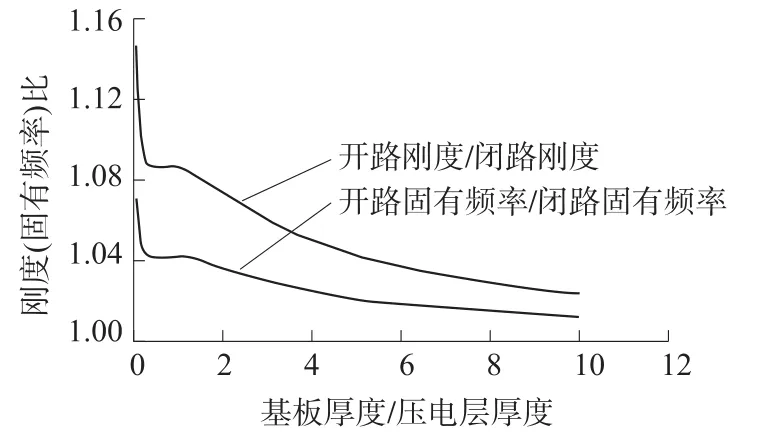
图5　单晶片压电梁的刚度比和固有频率比随厚度比变化规律

从图5中可以看出，刚度和固有频率变化规律一致，仅范围不同；在相同厚度比下，刚度的调节范围要大于固有频率的调节范围；当厚度比位于0～2时，频率调节范围较宽，但是，当厚度比小于1时，压电梁的中性轴不在基板内而位于压电层，压电片不能完全拉伸或压缩，无法输出最大能量，这时模拟的刚度已脱离真实状态。据此，要使单晶片压电梁稳定工作和具有较大频率调节范围，应选择厚度比为1或略大于1。

固定压电调节层厚度，改变基板与压电收集层的厚度，分析双晶片压电梁A的厚度比对刚度和固有频率调节范围的影响，分析结果如图6所示。

图6　双晶片压电梁A的刚度比和固有频率比随厚度比的变化规律

在图6（a）中，x轴为基板厚度与压电调节层厚度比，y轴为压电收集层厚度与压电调节层厚度比，z轴为开路刚度与短路刚度比；在图6（b）中，z轴为开路固有频率与短路固有频率比。从图6中看出，与单晶片压电梁类似，当厚度比越小时，刚度比越大，双晶片压电梁A固有频率可调范围也越宽。这是由于厚度比较小时，压电调节层相对较厚，刚度和固有频率可调范围相对较大；当两厚度比相同时，由于梁的中性轴位于压电调节层内，振动时刚度调节特性受到影响，刚度比急剧下降。

固定压电调节层厚度，改变基板与压电收集层的厚度，分析双晶片压电梁B厚度比对刚度和固有频率调节范围的影响，分析结果如图7所示。从图7中可以看出，厚度比越小，刚度和固有频率可调范围越大；在两个厚度比中，任一厚度比大于2时，其刚度和固有频率调节范围将显著下降。

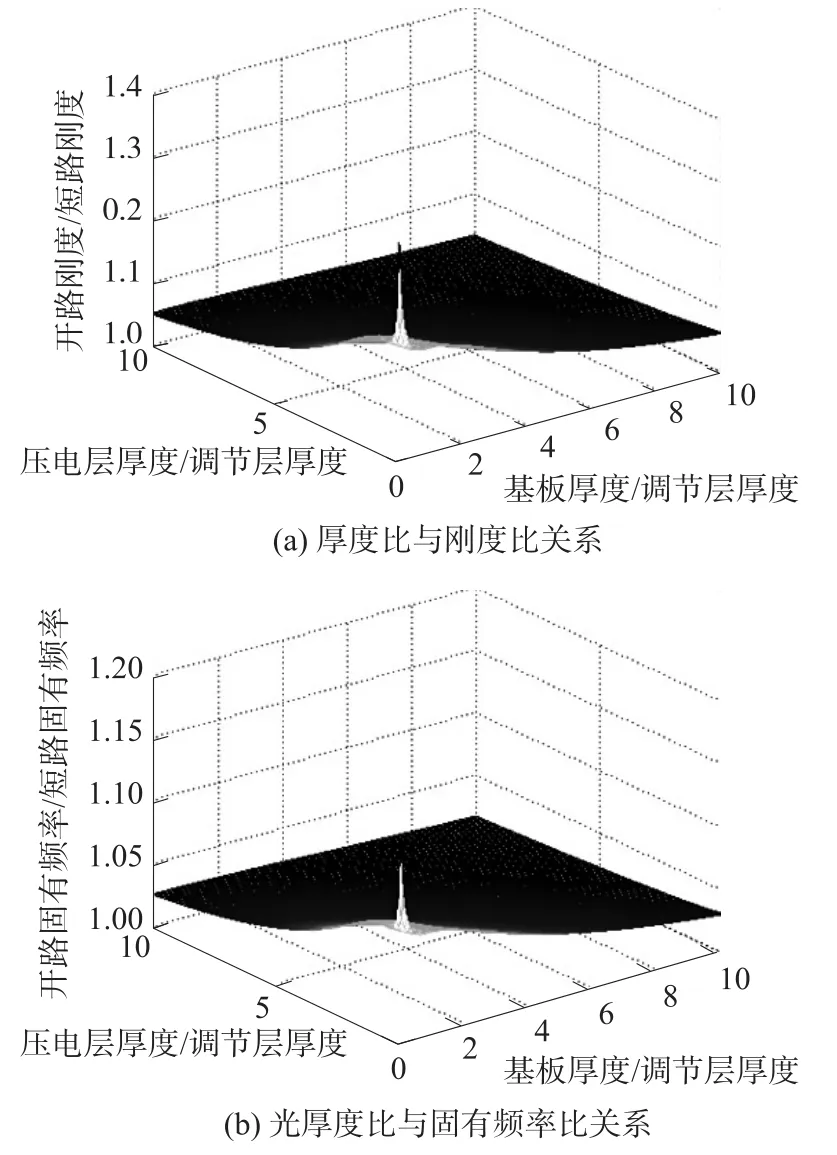
图7　双晶片压电梁B的刚度比和固有频率比随厚度比的变化规律

固定压电调节层厚度，改变基板与压电收集层的厚度，分析双晶片压电梁C的厚度比对刚度和固有频率调节范围的影响，分析结果如图8所示。对比图7可以发现，由于双晶片压电梁B和双晶片压电梁C两种结构的压电调节层所处的相对位置一致，因此两者的厚度比对刚度比及固有频率比的影响规律相似，仅调节范围值略有差异。

当双晶片压电梁C的两压电层均为调节层时，分析厚度比对刚度和固有频率调节范围的影响，分析结果如图9所示。从图9中可以看出，当基板与调节层厚度比约为1、收集层和调节层厚度比在0.3～0.5之间时，固有频率可调节范围较宽；当基板与调节层厚度比小于0.5时，刚度和固有频率调节范围迅速减小；相对其它配置，该结构的固有频率可调节范围最大。

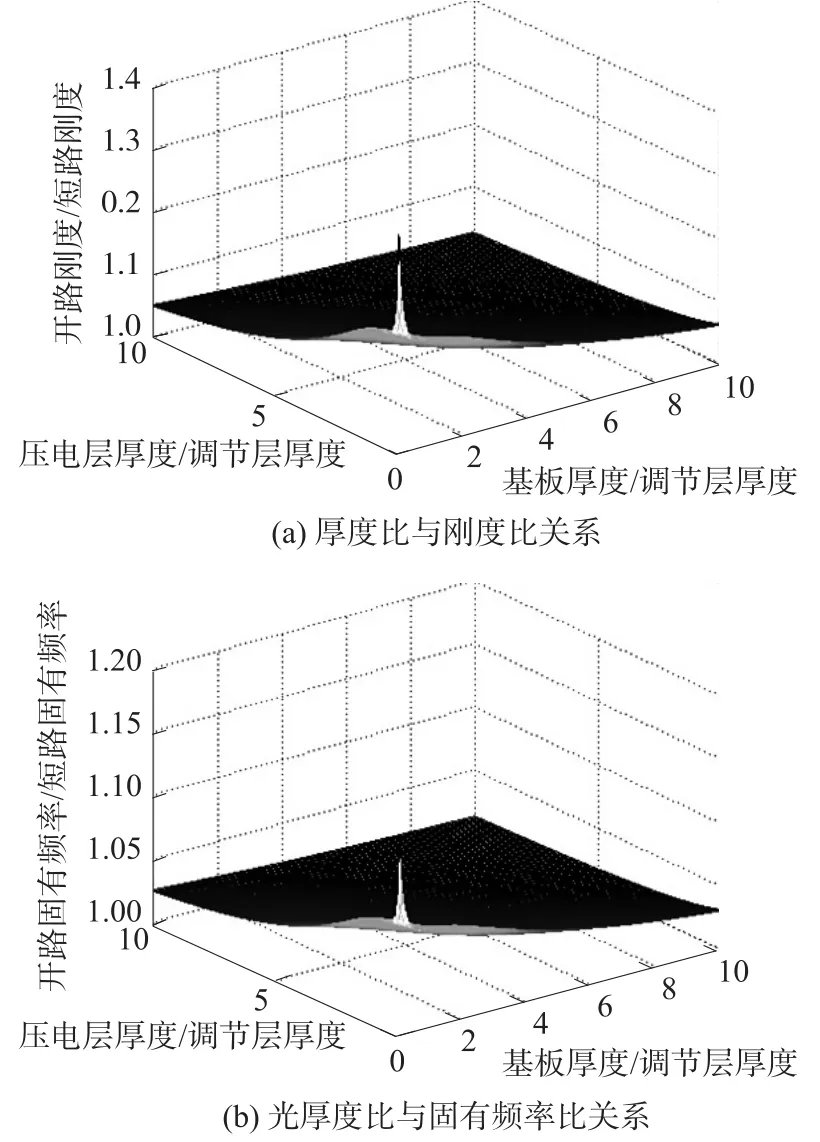
图8　双晶片压电梁C的刚度比和固有频率比随厚度比的变化规律

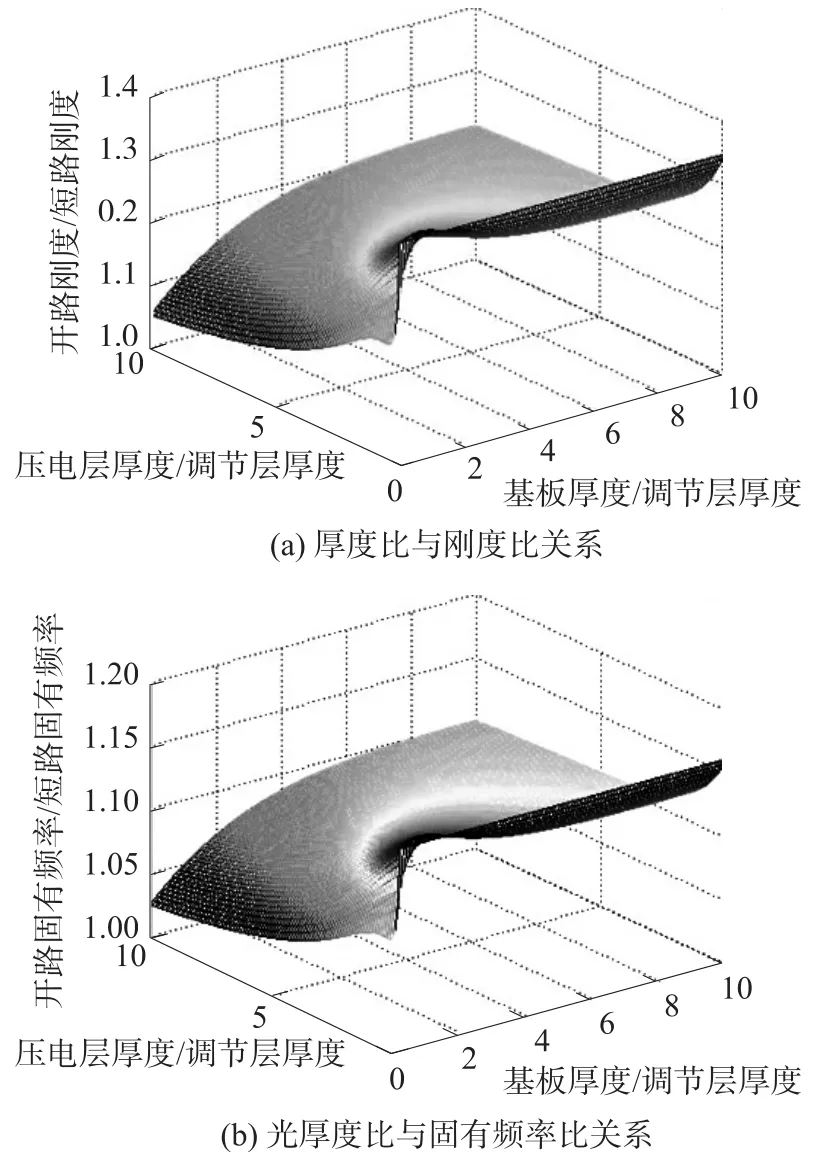
图9　两压电层调节的双晶片压电梁C的刚度比和固有频率比随厚度比的变化

通过以上分析可知，双晶片压电梁A和双晶片压电梁B的最大频率调节范围低于单晶片压电梁，且加工成本高，振动性能不稳定。因此，为提高频率调节范围和降低加工成本，应优先选用单晶片压电梁。另外，由于双压电层调节的双晶片压电梁C刚度比和固有频率比的变化范围较大，并且振动性能稳定，因此，也应作为重点选用对象。

2.3长度和宽度对旁路电容频率调节范围的影响

固定厚度比和材料参数，分别改变长度值和宽度值，分析长度、宽度对旁路电容频率调节范围的影响规律，分析结果如图10和图11所示。从图10和图11中可以看出，长度和宽度的变化对固有频率的调节范围没有任何影响。

图10　电容频率调节范围与长度的关系

图11　宽度与电容频率调节范围的关系

3　结论

为了实现旁路电容对压电式振动发电机固有频率的有效调节，分析了压电电容对振动发电机固有频率影响的基本规律，研究了结构和材料参数对压电梁固有频率比的影响特性，得出如下结论：

（1）压电调节层的开路固有频率与短路固有频率之比决定了悬臂梁压电发电机固有频率调节范围；旁路电容与压电电容比值小于5时，频率调节效果明显。

（2）单晶片压电梁和双晶片压电梁C的固有频率调节范围要优于双晶片压电梁A和双晶片压电梁B。

［1］阚君武，王淑云，彭少锋，等.多振子压电发电机的输出特性［J］.光学精密工程，2011，19（9）：2108-2116.

［2］张永良，林政.海洋波浪压电发电装置的进展［J］.水力发电学报，2011，30（5）：145-148，169.

［3］张磊，房立清，郭德卿，等.单晶压电振子结构二维优化设计［J］.压电与声光，2013，35（6）：889-892.

［4］蒋树农，郭少华，李显方，等.单压电片悬臂梁式压电俘能器效能分析［J］.振动与冲击，2012（19）：90-94.

［5］王兆强，刘海利，徐天柱，等.谐振式压电叠堆的高效换能结构研究［J］.振动与冲击，2011，30（12）：125-128.

［6］刘祥建，陈仁文.压电振动能量收集装置研究现状及发展趋势［J］.振动与冲击，2012，31（16）：169-176.

［7］林伟，卿辉，陈文，等.基于新型电源供电的无线传感网络节点设计［J］.压电与声光，2011，33（3）：498-500，508.

［8］何青，闫震.压电振动发电机理论建模与发电性能研究［J］.河北农业大学学报，2012，35（1）：106-110.

［9］闫震，何青.激励环境下悬臂梁式压电振动发电机性能分析［J］.中国电机工程学报，2011，31（30）：140-145.

［8］Ericka M，Vasic D，Costa F，et al.Energy Harvesting from Vibration Using a Piezoelectric Membrane［J］.Journal De Physique Iv，2005，128：187-193

［9］Wang S，Kwok H L，Sun C L，et al.Energy Harvesting with Piezoelectric Drum Transducer［J］.Applied Physics Letters，2007，90（11）：113506-113509.

［10］Nesbitt W Hagood，Walter H Chung，Andreas Von Flotow.Modelling of Piezoelectric Actuator Dynamics for Active Structural Control［J］.Journal of Intelligent Material Systems and Structures，1990，1（3）：327-354.

［11］单辉祖.材料力学Ⅱ［M］.北京：高等教育出版社，1999：15-19.

［12］William W Clark.Vibration Control with State-Switched Piezoelectric Materials［J］.Journal of Intelligent Material Systems and Structures，2000，11（4）：263-272.

闫震（1976-），男，河北保定人，讲师，博士（后），主要从事无线传感器网络及微能源技术的研究工作，参与及主持国家863计划，河北省自然科学基金等多项课题的研究，已发表相关学术论文20余篇，申请及获批专利5项，qceftgh@126.com。

Study on Piezoelectric Vibration Generator Based on Shut Capacitor Frequency Regulation Technology*

YAN Zhen1*，HE Qing2，WANG Dongping3，LIU Junfeng1
（1.Mechanic&Electronic College，Agricultural University of Hebei，Baoding Hebei 071001，China；2.School of Energy Power and Mechanical Engineering，North China Electric Power University，Beijing 102206，China；3.Department of modern science&technology，Agricultural University of Hebei，Baoding Hebei 071001，China）

Piezoelectric vibration generator made in MEMS can infinite and continue to supply energy for low power electric device.For adapting change of vibration source frequency，theoretical modeling and numerical analysis are adopted，and key technology of shunt capacity regulating inherent frequency is studied to enhance energy conversion efficiency of vibration generator.Mechanical model between piezoelectric capacitance and Young modulus of piezoelectric layer is established to analyze influence rule of piezoelectric capacitance to inherent frequency of piezoelectric generator，and capacitance frequency adjustment allocation plan of unimorph and bimorph beam are put forward；influencing characteristic of thickness ratio，length，width and material parameter to open circuit，closed circuit stiffness ratio and inherent frequency ratio is studied respectively，and optimal configuration of structural and material parameter is conducted.

wireless sensor network；piezoelectric vibration generator；shut capacitor；inherent frequency

TH122

A

1005-9490（2016）05-1067-06

项目来源：河北省自然科学基金项目（E2013204069）；保定市科学研究与发展计划项目（13ZG020；13ZF005）；河北农业大学理工基金项目（LG201401）

2014-12-25修改日期：2015-01-27

EEACC:834010.3969/j.issn.1005-9490.2016.05.010