基于二维PIC-DSMC的微间隙气体放电等离子体演化过程研究*

徐　翱，尚绍环，金大志，谈效华

（中国工程物理研究院电子工程研究所，四川绵阳621900）

基于二维PIC-DSMC的微间隙气体放电等离子体演化过程研究*

徐翱*，尚绍环，金大志，谈效华

（中国工程物理研究院电子工程研究所，四川绵阳621900）

准确的理解微间隙气体放电中非平衡等离子随时间的演化过程对于设计气体开关、微电子及其它等离子体器件有着非常大的帮助。通过二维PIC-DSMC耦合算法模拟了一个大气压氮气环境下微间隙平板电极发生气体放电时电子及离子的运动演化过程，得到了气体放电过程中平板电极间电子和离子数密度分布随时间变化的趋势，讨论了阳极附近电子云的形成与演变、阴极附近存在的鞘层以及电子和离子的速度及温度分布，最后将模拟计算得到的击穿电压与帕邢曲线及相关实验结果进行了对比，为相关等离子体器件的进一步发展提供了理论基础。

放电；网格质点法；直接模拟蒙特卡罗法；等离子体

随着近些年来等离子体计算模型及诊断技术的不断发展，直流或脉冲条件下的微间距气体或真空击穿研究受到了研究人员的广泛关注［1-5］。但是由于微间隙的极间距一般在微米量级，通过传统的等离子体诊断方法能够得到的相关信息仍然非常有限，而电学测量方法只能得到击穿过程的电压与电流关系，因此通过粒子模拟的方法获得微间隙气体放电过程的行为特性就成为了相关研究的重点。Zhang、Lee和Radmilovic-Radjenovic等人［6-8］首先使用PIC方法实现了微间隙气体放电的数值模拟，并将计算得到的击穿电压与实验结果进行了比较。2012年美国Sandia国家实验室的Moore等人在PIC的基础上引入了PIC-DSMC混合算法实现了对大气条件下微间隙平板电极气体放电的一维模拟［9］，得到了更多的气体放电行为特性。2013年Moore等人又利用一维PIC-DSMC算法分析了微间隙平板电极中不同背景中性气体密度对放电的影响［10］。但目前的这些研究基本都集中在如何实现数值模拟结果与帕邢曲线或实验测得的击穿电压相符，对微间隙气体放电过程中阳极附近电子云的形成与演变、阴极附近的鞘层、间隙中正离子及电子的运动导致的等离子体通道形成等过程并没有详细的报道，而这些却是能够证实数值模拟能够真正解释微间隙气体放电物理现象的重要部分。因此本文基于二维PIC-DSMC耦合算法模拟了一个大气压氮气环境下微间隙平板电极发生气体放电时电子及离子的运动行为和等离子体通道的形成过程，并对其中等离子体的相关特性进行了分析，为相关等离子体器件的进一步发展提供了坚实的基础。

1　计算模型

PIC-DSMC（网格质点法-直接模拟蒙特卡罗法）耦合算法是一种可以较好的模拟等离子体运动演化过程的数值模拟方法。本文模拟使用的PICDSMC耦合算法由PIC模块与DSMC模块组成，其中PIC模块处理所有带电粒子的运动、电场的计算、粒子与电极的作用、粒子间发生的电离、复合等化学反应，而DSMC处理中性粒子的运动，这样就能够满足气体击穿过程包含电子、离子和中性粒子等多种类复杂运动的模拟需要。

实际物理模型是间隙为d的两个对称的圆形平板电极，因此可以用二维圆对称模型来进行模拟，即只需模拟两电极中心对称轴与电极之间的二维区域来表征整个物理模型。假设模拟区域的电极半径r=20 μm，电极间隙d=50 μm，模拟模型如图1所示。

图1　模拟模型

模拟初始时刻两电极间充满均匀分布的常温（20℃）氮气，其压强为1个标准大气压，另外此时电极间还存在均匀分布的游离自由带电粒子，假设其为电子和氮气离子，数密度都为1×1015m-3。文献［10-11］中一般要求设置初始电子离子数密度小于中性粒子密度的1/109，通过反复计算可以发现微间隙气体击穿模拟中初始电子离子数密度的设置值在1015m-3量级附近，变化±1个量级对计算得到的击穿电压值基本没有影响，仅仅对等离子体通道形成时间有一定影响，因此设置初始电子离子密度为1×1015m-3）。同时使得阴极接地，阳极电压设为570 V，考虑多种电子、离子及中性粒子间的碰撞及激发、电离、复合等化学反应，如表1所示，所使用的相关碰撞及反应截面数据见文献［12-14］，而中性粒子间的弹性碰撞由DSMC模块直接计算。

表1　碰撞及化学反应

PIC的网格及时间步长的选取原则［15］一般为网格Δx≤λD，其中λD表示德拜长度；而时间步长Δt≤0.2/ωpe，其中ωpe表示等离子体角频率。考虑到发生气体击穿时的数密度一般在1020m-3量级左右，而电子温度在几eV到几十eV量级，因此模拟时选择PIC模块的网格为边长0.5 μm的正方形网格，时间步长为1×10-13s。同时由于DSMC的网格及时间步长选取原则［16］一般为网格Δx≤λ/3，其中λ表示平均自由程；时间步长Δt≤Δx/vmax，其中vmax表示该方向粒子的最大速度，而发生气体击穿时平均自由程一般都大于德拜长度（假设电子温度为1 eV，则模拟条件下的电子平均自由程约4.5 μm，而对应的德拜长度为约0.74 μm），因此可以设置DSMC模块与PIC模块使用同一套网格，但DSMC的时间步长设置为1×10-12s，即每运行10次PIC程序，运行1次DSMC程序。而考虑发生击穿时仿真分子的数量为每个网格有约80个代表电子、80个代表离子和40个代表中性粒子，则可以设置最大仿真分子数为80万个。并且每个仿真分子代表的真实粒子权重在程序中可以自动调整。

模拟考虑的两个电极均为清洁表面的铜电极，假设中性粒子与电极表面的作用为反射率为1的漫反射，而使用的电子轰击电极表面产生的二次电子率曲线见参考文献17，离子轰击电极表面产生的二次电子率由下式得到［18］：

其中Eiz，s表示入射离子的电离能，Eφ表示以eV为单位的功函数。最后在模拟过程中监控电极间的传导电流，如果发现传导电流迅速增加则认为等离子体通道已经形成，气体击穿即将发生，模拟计算中止。

2　微间隙气体放电等离子体演化过程分析

微间隙气体放电的物理特征就是一个在微间隙中形成等离子体通道并导通的过程，因此通过PIC-DSMC耦合算法计算发生气体击穿时电子、N2+及N+的数密度分布随时间变化就可以得到微间隙气体放电的演化过程。假设电极加电压的瞬间为初始时刻t=0，则计算得到的t=1 ns、3 ns、5 ns、8 ns、10 ns和12 ns时电子、N2+及N+的数密度在整个模拟计算区域中的分布云图如图2～图4所示，这些图的左侧为阴极，右侧为阳极，下端为对称轴，与图1所示一致。

图2　电子数密度分布云图

通过图2可以发现，t=1 ns时阳极附近形成电子云，这应该是由于间隙中的游离电子受阳极的吸引向阳极附近运动并且获得了一定的能量，再由于电子轰击阳极产生的二次电子，这会造成在阳极附近出现许多电子并且大量电离背景气体产生更多的电子，从而形成阳极附近的电子云；而随着时间增加到t=5 ns左右时阳极附近的电子数密度、电子分布区域都呈现减小的趋势，这是由于电子不断向阳极运动，而通过电子电离背景气体产生的电子数量少于被阳极俘获的电子数量，从而造成电子数密度及电子分布区域都减小；但随着时间增加到t=8 ns左右时阳极附近的电子数密度继续减小，但阴极附近出现电子并且电子分布区域出现增大的趋势，这是由于正离子轰击阴极产生了二次电子，这些二次电子又迅速向阳极运动且运动过程中又电离产生了新的电子从而造成电子分布区域增大，另外此时紧挨阳极的附近出现高电子数密度区域，这可能与电子轰击阳极产生的二次电子又被阳极吸引从而又轰击阳极产生新二次电子这样的循环过程有关；最后时间增加到t=12 ns左右时电子已经能够形成通道，这是由于正离子轰击阴极产生二次电子，二次电子向阳极运动时又不断产生新的电子和正离子，而这些新的正离子会向阴极运动并轰击阴极产生二次电子，如此循环从而导致电子通道的形成。

图3　N2+数密度分布云图

通过图3可以发现t=1 ns时阳极附近同样会形成N2+云，这说明阳极附近确实存在大量的电离；而随着时间增加到t=5 ns左右时阳极附近的N2+云的高数密度中心出现向阴极方向的移动，这是由于受阴极的吸引向阴极运动，但N2+的速度比电子速度慢，因此其数密度分布变化不是特别明显；但随着时间增加到t=8 ns左右时N2+云的高数密度中心出现明显扩散开的趋势，靠近阴极附近的N2+数密度也明显增加，而阳极附近却出现显著的N2+数密度减小，这些都与电子数密度分布的变化契合，进一步表明了正离子轰击阴极产生二次电子，这些二次电子迅速向阳极运动且运动过程中又电离产生了新的电子和正离子从而导致区域内等离子体密度增大，同时阳极附近的电子轰击阳极产生二次电子被吸引轰击阳极又产生新的二次电子这样的循环过程中电子难以获得足够的能量来电离背景气体，所以正离子数量明显减小；最后时间增加到t=12 ns左右时N2+已经在微间隙内形成了明显的通道。

图4　N+数密度分布云图

对比图3与图4可以发现，N+的数密度分布随时间变化趋势与N2+比较类似，但是N+的变化稍稍快一些，这是由于其质量较小，因此变化速度相对较快。另外N+的数密度明显小于N2+，这是由于背景气体主要是N2，而N需要由N2通过离解等反应才能产生，因此相对较少，再将N电离才能产生N+的数量就更少。

通过分析1 ns、6 ns和12 ns时靠近对称轴线区域（由于所使用的软件无法提取对称轴线上的相关数据，因此选择非常靠近对称轴线的区域，即r=0.3 μm来代表对称轴区域）的电场及电势变化，如图5和图6所示，可以发现阴极附近（靠近x=0）的电场和电势都随着时间t的增加而增大，并且其随着x增大而变化的趋势也更加剧烈；而阳极附近（靠近x=50 μm）的电场随着时间t的增加而减小，电势随着时间t的变化不大，但其随着x减小而变化的趋势变得相对平缓。这说明了阴极附近应该会形成鞘层，并且该鞘层随着时间t增加而变得更加明显。而阳极附近并没有形成明显的鞘层，这可能是由于阳极附近随着时间t增加形成了靠近阳极的高数密度电子云，但该电子云没有能够电离出足够多的正离子，从而使得该区域变成了“电子通道”而不是鞘层。

图5　r=0.3 μm处的电场分布

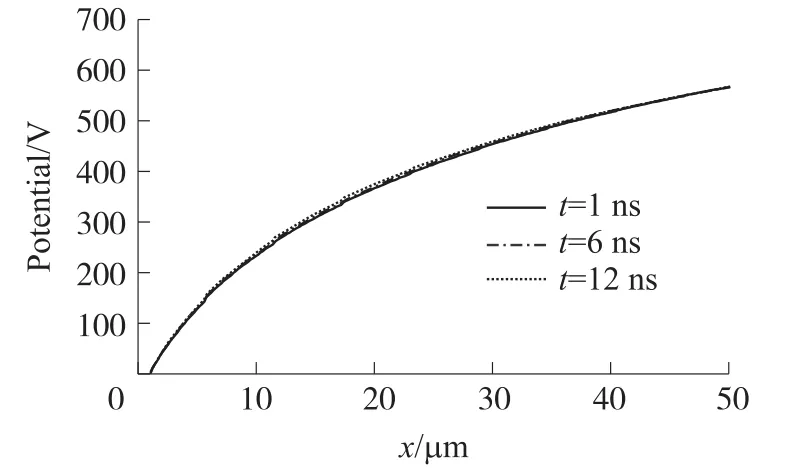
图6　r=0.3 μm处的电势分布

通过分析12 ns时靠近对称轴线区域（r=0.3 μm）的电子速度及N2+速度，如图7所示，可以发现电子速度大于N2+速度2-3个数量级，这证明了离子运动确实比电子运动慢；另外电子速度在阴极附近有明显突增，然后从阴极向阳极稍有减小，这可能是由于电子离开阴极后立即受到强静电场作用使其速度突增，但随后静电场减小并且电子会不断的与氮气发生碰撞从而又使其速度有所降低；而N2+主要是由电子碰撞电离产生，产生后就会受到静电场作用不断使其加速，又由于其仍然会与氮气等碰撞从而减速，因此其在大部分区域的速度都比较相似，但随着其靠近阴极，静电场会明显增加，因此靠近阴极的N2+速度明显增大。而通过12 ns时靠近对称轴线区域（r=0.3 μm）的电子温度及N2+温度，如图7所示，可以发现电子温度同样大于N2+温度1个数量级，并且它们的分布趋势与速度分布趋势类似。

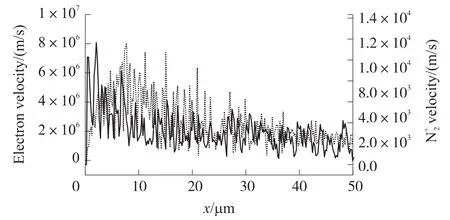
图7　r=0.3 μm处的电子速度和N2+速度

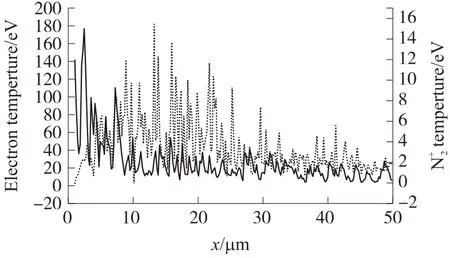
图8　r=0.3 μm处的电子温度和N2+温度

模拟计算得到的电极上收集到的电流与时间t的关系如图9所示，可以发现t=12 ns左右时电流会迅速增加，因此可以认为等离子体通道形成，微间隙内将会发生放电。而基于相似的初始条件设置可以模拟计算得到不同间距微间隙的击穿电压，并与帕邢曲线计算得到的击穿电压及参考文献4实验测试得到的击穿电压相比，如图10所示，可以发现模拟计算得到的击穿电压比帕邢曲线及实验测试得到的击穿电压稍高一些，但曲线变化趋势基本相似，造成这样的原因可能是由于模拟中没有考虑到激发态原子退激后产生的光辐射会造成光致电离，以及离子轰击电极产生二次电子率公式比较简单等。但是仍然可以认为通过PIC-DSMC耦合算法能够较为准确的模拟计算得到微间隙气体放电的物理过程。

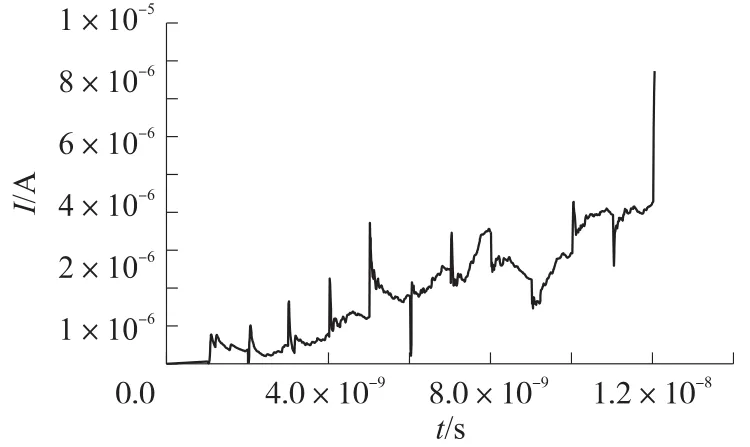
图9　电流与时间的关系

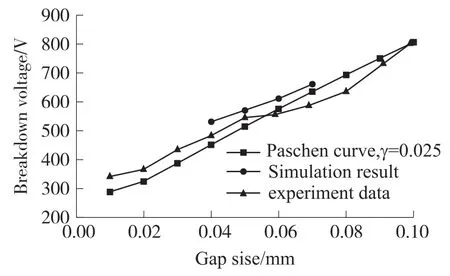
图10　击穿电压与间距的关系

3　结论

通过与帕邢曲线及实验结果比较，可以认为基于PIC-DSMC耦合算法能够较为准确的获得气体放电特性曲线，因此其模拟得到的放电形成过程中电子和离子的运动演化过程及相关等离子体参数时空分布规律能够反映真实气体放电过程的情况，所以通过对这些气体放电等离子体演化过程研究就可以为设计气体开关、微电子及其它等离子体器件打下坚实的理论基础。

［1］Hitchon W N.The Time History of Reakdown［J］.J Phys D：Appl Phys，2008，41（22）：222002.

［2］Sshnyder R，Howling A A，Bommottet D，et al.Direct Current Breakdown in Gases for Complex Geometries from High Vacuum to AtmosphericPtrssure［J］.JPhysD：ApplPhys，2013，46（28）：285205.

［3］Venkattraman A.Generalized Criterion for Thermo-Field Emission Driven Electrical Breakdown of Gases［J］.Applied Physics Letters，D2014，104（19）：194101.

［4］Radmilovic-Radjenovic M，Radjenovic B，et al.The Breakdown Phenomena in Micrometer Scale Direct-Current Gas Discharges［J］.Plasma Chem Plasma Process，2014，34：55-64.

［5］卢新培，严萍，任春生，等.大气压脉冲放电等离子体的研究现状与展望［J］.中国科学：物理学力学天文学，2011，41（7）：801-815. Lu Xinpei，Yan Pin，Ren Chunsheng，et al.Review on Atmospheric Pressure Pulsed DC Discharge.Scientia Sinica Phys.Mech& Astron，2011，41（7）：801-815.

［6］酉小广，成永红，孟国栋，等.微机电系统微尺度间隙的脉冲击穿特性［J］.强激光与粒子束，2013，25（7）：1867-1872. You Xiaoguang，Cheng Yonghong，Meng Guodong，et al.Pulse Breakdown Characteristics of Microscale Gap in Micro-Electro-Mechanical System.High Power Laser and Particle Beams，2013，25（7）：1867-1872.

［7］Zhang W，Fisher T S，Garimella S V.Simulation of Ion Generation and Breakdown in Atmospheric Air［J］.Journal of Applied Physics，2004，96（11）：6066-6072.

［8］Lee S M，Seo Y S，Lee J K.Paschen Breakdown Curve by One-Dimensional PIC-MCC Simulation［J］.Computer Physics Communications，2007，177：132.

［9］Radmilovic-Radjenovic M，Radjenovic B.A Particle-in-Cell Simulation of the Breakdown Mechanism in Microdischarges with an Improved Secondary Emission Model［J］.Contrib.Plasma Phys.，2007，47（3）：165-172.

［10］Moore C H，Hopkins M M，Crozier P S，et al.1D PIC-DSMC Simulations of Breakdown in Microscale Gaps［C］//28th International Symposium on Rarefied Gas Dynamics，2012：629-636.

［11］Moore C H，Hopkins M M，Boerner J J，et al.PIC Simulation of Microscale Breakdown in Gaps Having a Non-Uniform Background Neutral Gas Density［C］//31th ICPIG，2013：10-13.

［12］Yukikazu I.Cross Sectrions for Electron Collisions with Nitrogen Molecules［J］.J Phys Chem Ref Data，2006，35（1）：31-53.

［13］Phelps A，Pitchford L.Anisotropic Scattering of Electrons by N2and Its Effect on Electron Transport［J］.Phys Rev A，1985，31（5）：2932-2949.

［14］Straub H C，Renault P，Lindsay B G，et al.Absolute Partial Cross Sectrions for Electron-Impact Ionization of H2，N2and O2from Threshold to 1 000 eV［J］.Physical Reviwe A，1996，54（3）：2146-2153.

［15］Tskhakaya D，Matyash K，Schneider R，et al.The Particle-In-Cell Methode［J］.Contrib Plasma Phys，2007，47（8-9）：563-594.

［16］Bird G A.Molecular Gas Dynamics and the Direct Simulation of Gas Flows［M］.Oxford：Oxford University Press，1994：334-369.

［17］Walker C G H，El-Gomati M M，Assa'd A M D，et al.The Secondary Electron Emission Yield for 24 Solid Elements Excited by Primary Electrons in the Range 250 eV～5 000 eV：A Theory/Experiment Comparisom［J］.Scanning，2008，30（5）：365-380.

［18］Lieberman M，Lichtenberg A.Principles of Plasma Discharges and Materials Processing［M］.New Jersey：Wiley，2005：299-320.

徐翱（1982-）男，汉族，湖北武汉人，就职于中国工程物理研究院电子工程研究所，副研究员，博士。主要研究方向为等离子体技术及电真空器件研制，xuao@caep.cn。

Study on Plasma Evolution in Microscale Gas Discharge Based on Two Dimension PIC-DSMC Code*

XU Ao*，SHANG Shaohuan，JIN Dazhi，TAN Xiaohua
（Institute of Electronic Engineering，China Academy of Engineering Physics，Mianyang Sichun 621900，China）

It is helpful to exactly understanding non-equilibrium plasma evolution in microscale gas discharge for designing gas switch，microelectronics and other plasma device.The gas discharge in microscale gap size under one atmospheric pressure of N2environment is simulated by a PIC-DSMC code.The kinetic evolution process of electron and ions in this gas discharge is presented，and the distribution of electron density and ion density varied with discharge time is obtained.Then，the formation and change of the electron cloud near anode，the sheath near cathode，and the distribution of velociy and temperture are discussed.Finally，the simulation result is compared with Paschen curve and experiment data.It can provide theoretic help for furher development of plasma device.

discharge；PIC；DSMC；plasma

O461.1

A

1005-9490（2016）05-1025-06

项目来源：中国工程物理研究院科学技术发展基金项目（2015B0102013）；中国工程物理研究院电子工程研究所科技创新基金项目（S20150807）

2015-10-22修改日期：2015-11-10

EEACC:231510.3969/j.issn.1005-9490.2016.05.001