转捩对压缩拐角激波/边界层干扰分离泡的影响

童福林， 李新亮， 唐志共,*， 朱兴坤， 黄江涛

1.中国空气动力研究与发展中心 计算空气动力研究所， 绵阳 6210002.中国科学院 力学研究所 高温气体动力学重点实验室， 北京 100190

转捩对压缩拐角激波/边界层干扰分离泡的影响

童福林1， 李新亮2， 唐志共1,*， 朱兴坤2， 黄江涛1

1.中国空气动力研究与发展中心 计算空气动力研究所， 绵阳 6210002.中国科学院 力学研究所 高温气体动力学重点实验室， 北京 100190

为了研究转捩对压缩拐角内分离泡结构的影响，进行了来流马赫数2.9，24° 压缩拐角激波/转捩边界层干扰的直接数值模拟(DNS)。通过在拐角上游平板的不同流向位置处添加周期性吹吸扰动激发流动转捩，使得转捩不同阶段进入拐角入口，从而在拐角内产生激波/转捩边界层的相互干扰。计算得到的平均速度剖面、壁面压力分布以及分离泡大小与风洞试验及以往直接数值模拟结果吻合较好，验证了计算结果的可靠性。研究了转捩过程对角部干扰区内分离泡结构的影响规律，分析比较了不同转捩阶段下角部分离区内湍动能的生成、耗散和分配机制。研究结果表明：转捩初期的拟序涡结构对分离泡尺度及形状影响最大，发卡涡包在角部拐点附近发生展向融合，并在角部区域形成湍流斑，此时分离泡尺度最小，形状呈现中间高两边低的山峰型。随着转捩的发展，分离区内湍动能生成和近壁区的耗散逐步降低，此时输运项起到了主要的平衡作用。

转捩； 压缩拐角； 激波/边界层干扰； 分离泡； 直接数值模拟

压缩拐角激波/边界层干扰是高速飞行器上广泛存在的典型流动问题，它会导致飞行器物面边界层出现非定常大尺度分离现象。这些分离泡引起的强压力脉动使得飞行器局部结构出现疲劳载荷，极大地缩短了飞行器结构使用寿命。另外，Plotkin[1]、Poggie和Smits[2]以及Touber和Sandham[3]的研究表明，飞行器上游低频扰动在分离泡(放大器)的作用下也会对飞行器下游结构及飞行性能产生严重影响。自20世纪50年代以来，大批学者对该问题进行了大量研究[4-6]。但是，以往大部分的工作都是集中在激波/层流或湍流干扰，较少考虑转捩的影响。随着当前飞行器发展，激波/转捩边界层干扰很有可能出现在高速飞行器进气道或其他外部位置[7]。因此，分析研究转捩对压缩拐角激波/边界层干扰分离泡的影响在工程应用中具有重要意义。

目前，关于转捩对激波/边界层干扰分离泡的影响，现有的工作已取得了一些进展和初步认识。Chapman等[8]研究了马赫数Ma=3的压缩拐角激波/转捩边界层干扰流动，发现转捩点与分离起始点及再附点的相对位置对分离泡尺度有较大影响。Murphree等[9]试验研究了圆柱诱导激波/边界层干扰问题。结果表明，与层流和湍流干扰相比，转捩下的分离区尺度及形状具有强非定常性和展向非均匀性。Vanstone等[10]研究了转捩过程中湍流斑对激波诱导边界层分离泡的影响作用，发现在湍流斑足够大情况下，层流分离泡会局部演化为完全再附湍流，而且流动中出现明显的瞬时三维特征。Giepman等[11]采用高分辨率粒子成像测速技术测量了入射激波/边界层干扰流动，观察到完全湍流情况下边界层没有发生分离，而转捩下出现了分离区，但分离泡的尺度要明显小于层流干扰情况。Polivanov等[12]也发现了转捩对激波/边界层分离泡有较好的抑制作用。总体来看，已有的认识多为试验观测认知，转捩对干扰区内分离泡的影响机制尚不十分清楚，急需开展相关方面的机理研究。

当前，由于直接数值模拟(Direct Numerical Simulation，DNS)不引入任何湍流模型或亚格子应力模型，同时能够直接求出所有尺度的湍流脉动的时空演化信息，具有较高的可靠性。因此，近些年来，DNS在激波/边界层干扰的流动机理研究方面得到广泛地应用[13-16]。为了研究转捩的演化发展历程对激波/边界层干扰分离泡的作用机制，本文进行了来流马赫数Ma∞=2.9，24° 压缩拐角激波/转捩边界层干扰的DNS。为了便于结果的验证，选取的计算参数尽量接近Ringuette[17]、Bookey[18]等的试验以及Wu和Martin[19]的DNS。本文在压缩拐角上游的平板采用添加周期性吹吸扰动的方法来激发流动转捩到湍流，通过改变平板的长度，从而使得进入拐角角部入口的流动处于转捩过程的不同阶段，如转捩初期、非线性增长段、转捩峰、层流破碎和完全湍流阶段等。

1 计算设置

控制方程为一般曲线坐标系下的三维可压缩Navier-Stokes方程组。采用无穷远来流参数对方程进行无量纲化，方程具体形式如下：

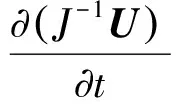
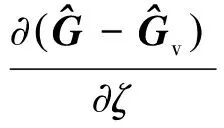
(1)

式中：U为守恒变量；E、F和G为无黏通量；Ev、Fv和Gv为黏性通量；t为时间；ξ、η和ζ为一般曲线坐标系；J-1为坐标系的Jacobin变换系数。无黏项采用Martin等[20]优化构造的WENO(Weighted Essetntially Non-Oscillatory)格式以及Steger-Warming流通量分裂方法求解。该格式是在8阶中心格式网格基架点上优化得到的，由于采用了对称网格基架点，格式具有很高的波数分辨率和较低的数值耗散。黏性项采用8阶中心差分格式进行离散，时间推进采用三阶Runge-Kutta方法计算。

计算模型为24° 压缩拐角，如图1所示。图中x、y和z分别为流向、法向和展向方向，坐标原点取拐角的拐点。压缩拐角流向跨度由角部区域(35 mm)和折面区域(51.5 mm)两部分组成，展向宽度为14 mm。来流马赫数Ma∞=2.9，基于单位长度的来流雷诺数Re∞=5 581.4 mm-1，来流静温为108.1 K，壁温取307 K。出口边界统一使用超声速出口无反射边界条件。物面边界为无滑移条件和等温壁。上边界取为简单无反射边界条件，展向为周期性条件。

图1 压缩拐角计算模型示意图Fig.1 Illustration of compression ramp

本文在压缩拐角入口(x=-35 mm)的上游添加了带有吹吸扰动带的平板(见图1)，通过改变平板长度Lp，使得进入拐角入口的流动处于转捩过程的不同阶段。因此，在实际计算过程中，为了确定不同转捩阶段对应的平板长度，首先需要对相同来流条件下超声速平板层流边界层在吹吸扰动作用下的转捩过程进行DNS。吹吸扰动带内壁面法向扰动速度分量的表达式为[21]

(2)

式中：xa和xb分别为扰动带的起点和终点位置；相位差φl和φm取0～1的随机数；lmax=10，mmax=5；z为展向坐标值；zmax为展向计算域宽度；A为扰动幅值，β为扰动频率，本文计算中取A=0.2，β=0.1。图2给出扰动带内法向扰动速度Vbs在xOz平面内的分布云图。从图中可以看到，引入的法向扰动速度在展向上存在非对称性。

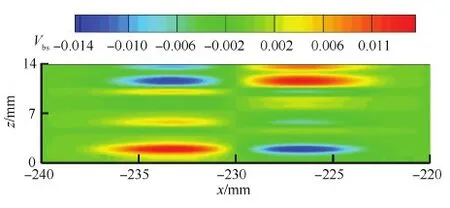
图2 吹吸扰动带内法向扰动速度Vbs的xOz分布云图Fig.2 Contour of normal disturbance velocity component Vbs in xOz plane

图3和图4分别给出了平板边界层转捩DNS得到的中截面瞬时温度T分布云图和平均摩擦阻力系数{Cf}分布。无特别说明，本文平均指的是展向及时间推进方向上的时空平均，以符号{}表示；时间平均以符号<>表示；图中各变量均为无量纲量。显然，平板层流边界层在壁面吹吸扰动作用下转捩到了充分发展湍流阶段。图4中还给出了根据当地动量厚度及Blasius湍流摩阻公式的理论预测值[21](图中：实线为本文DNS结果；三角形为理论预测值)。从图中可以看到，在湍流充分发展段，计算值与理论预测值在规律和量值上都基本吻合。

由图4可见，在-280 mm≤x≤-180 mm处壁面摩擦阻力系数大幅升高，这表明转捩已开始发生，转捩峰出现在x=-170 mm附近，而在>-160 mm≤x≤-40 mm处摩擦阻力系数平滑下降，这表明转捩过程已经逐渐完成，流动达到充分发展湍流阶段。依据Gao[15]和Li[16]等的分析，该转捩类型为旁路(Bypass)型转捩，转捩发展过程跳过了自然转捩中的不稳定扰动波的线性增长阶段，直接进入扰动波的非线性发展阶段，最终经过层流破碎发展到完全湍流。

图3 平板中截面(z=7 mm)瞬时温度分布云图Fig.3 Contour of instantaneous temperature in the middle section of flat-plate (z=7 mm)

图4 平板平均摩阻系数{Cf}分布Fig.4 Distribution of mean skin-friction coefficient {Cf} of flat-plate

为了研究转捩过程对压缩拐角内分离泡的影响，依次选取了该Bypass转捩过程的5个典型阶段进行比较分析，分别包括转捩起始(Case 1)、非线性增长段(Case 2)、转捩峰(Case 3)、层流破碎(Case 4)和完全湍流区(Case 5)，各阶段具体位置见图4。表1给出了各转捩阶段对应的平板长度Lp及拐角入口(x=-35 mm)处各转捩边界层参数，包括了边界层动量厚度θ、名义厚度δ、摩阻系数Cf及动量厚度雷诺数Reθ。表1中的所有长度尺度单位均为毫米，Cf为无量纲值，下文类似。

表1平板长度Lp及拐角入口处(x=-35mm)转捩边界层

Table1Lengthofflat-plateLpandboundarylayeratcornerinlet(x=-35mm)

CaseLp/mmCfδ/mmθ/mmReθ1650．000681．980．1583721150．001692．350．18100431650．002843．720．24133942250．002695．420．33184153000．002566．530．412288

表2不同转捩阶段对应的计算域及计算网格

Table2Computationaldomainandgridsatdifferenttransitions

CaseLx×Ly×LzNx×Ny×NzΔ+x×Δ+y×Δ+z1151．5×35×141110×160×1400．9×0．1×1．02201．5×35×141280×160×1403．4×0．4×3．93251．5×35×141440×160×1404．5×0．5×5．14321．5×35×141725×160×1404．3×0．5×4．95386．5×35×142160×160×1404．2×0．5×4．8

2 结果验证

为了验证计算结果的可靠性，本文将Case 5的结果(此时压缩拐角入口为完全湍流阶段)与Ringuette[17]、Bookey[18]等的试验及Wu和Martin[19]的DNS数据进行了对比验证。这里要特别说明的是，由于试验没有详细给出拐角上游的转捩过程以及转捩的触发方式，本文Case 5的流动参数只能尽量接近Ringuette等的试验，无法做到完全一致。另外，Wu和Martin的DNS采用的是循环重构方法生成完全湍流入口条件，与本文的入口参数也存在一定的差异。表3给出了三者在拐角入口边界层参数的比较。从表中可以看到，本文入口处边界层名义厚度和动量厚度与试验及DNS基本接近，但摩阻系数要高些。

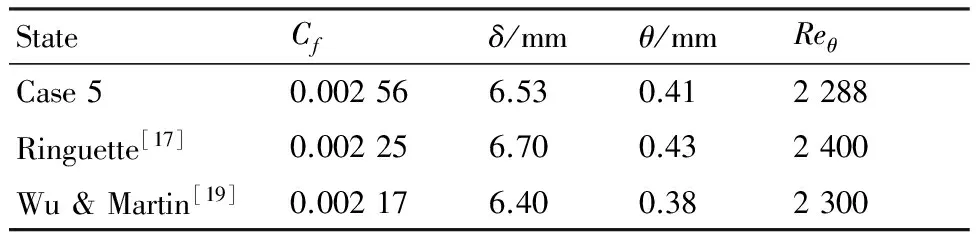
表3 拐角入口的边界层参数Table 3 Boundary layer parameters at corner inlet

图5分别给出了拐角内干扰区上游(Upstream Boundary Layer， Upstream BL)及下游x/δ=4处平均流向速度剖面。可以看到，在上游的无干扰区内，本文计算得到的边界层内速度型与试验结果及DNS数据均吻合较好。另外，在下游干扰区内的x/δ=4测点处，本文得到的边界层外层区域速度型与试验及DNS也较为一致，但是在近壁区域内，尽管本文与Wu和Martin的DNS数据分布规律较为一致，但均与试验测量值存在较大偏差，这很可能与风洞试验中物面近壁区的速度测量误差有一定的关联。

图5 拐角上游及干扰区x/δ=4处平均速度{U}分布Fig.5 Mean velocity {U} profiles at upstream boundary layers and x/δ=4

图6给出了压缩拐角物面平均压力{pw}分布与试验及DNS的比较情况，其中横坐标用x=-35 mm处的当地边界层名义厚度进行无量纲化。显然，本文计算得到物面平均压力分布与Wu和Martin[19]的DNS数据基本重合，且两者均在Bookey等[18]试验数据误差带(5%)的范围内。激波与边界层的相互作用导致壁面压力沿流向升高，在压力升高过程中出现了压力平台，这说明本文计算结果准确捕捉到了角部区域内边界层的分离。图7给出了压缩拐角干扰区内壁面平均摩阻系数{Cf}沿流向分布与试验及DNS结果的比较。在图7中，{Cf}小于0的区域代表流动分离区，与Wu和Martin[19]的结果相比(见表3)，由于角部入口处来流{Cf}偏高，抑制了角部分离泡的发展，导致本文计算得到的分离区起始点相比靠后，但本文计算的再附点位置与Ringuette等的试验值及Wu和Martin的DNS相比基本重合，而且拐角斜面上摩阻系数无论是在分布规律还是量级上都与Wu和Martin的DNS是一致的。

图6 压缩拐角物面平均压力分布Fig.6 Distribution of mean wall pressure of compression ramp

图7 压缩拐角物面平均摩阻系数分布Fig.7 Distribution of mean skin-friction coefficient of compression ramp

综上，本文采用的吹吸扰动激励流动转捩到湍流的方法是可行的，计算得到的分离泡尺度与试验[17-18]及DNS[19]吻合较好。

3 分析讨论

3.1 分离泡结构

图8给出了不同转捩阶段下角部干扰区内的平均摩阻系数{Cf}的分布。图中{Cf}依次为0的点分别代表分离区起始和再附点。图9和图10 分别给出了干扰区内流线分布和湍动能k云图。与完全湍流情况(Case 5)相比较，除了Case 1，各转捩阶段均抑制了角部干扰区内分离泡的发展。从Case 5到Case 2，分离点从x=-17.0 mm往拐点方向移动到x=-3.1 mm，再附点也往拐点方向从x=7.5 mm移动到x=1.8 mm，分离泡流向尺度依次逐渐减小。Case 4到Case 2的流向尺度分别为Case 5的70%、45%和20%。对于Case 1，可以看到分离区起始点已经明显超出了拐角入口，再附点较其他阶段也最为靠后(x=9.3 mm)，此时的分离泡流向和法向尺度均远大于完全湍流情况Case 5。

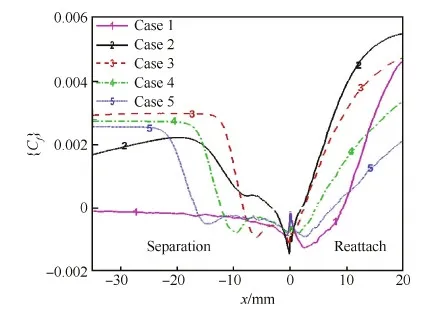
图8 不同转捩阶段下角部干扰区平均摩阻系数分布 Fig.8 Distribution of mean skin-friction coefficient at different transitions

图9 拐角干扰区内流线分布Fig.9 Distribution of streamlines in interaction region at ramp

图10 拐角干扰区内湍动能云图 Fig.10 Contours of mean turbulent kinetic energy in interaction region at ramp

图11给出了角部干扰区内时间平均摩阻系数沿展向分布情况。该图反映了分离泡流向尺度沿展向的分布规律。图中蓝色区域对应为Cf≤0的分离区，红色区域对应Cf>0。可以看到，从Case 1到Case 5，干扰区内再附点沿展向均出现不规则波浪结构,其中以Case 1和Case 2尤为明显；对于分离区起始点，从Case 3到Case 5，起始点沿展向宽度变化较小，但是Case 2的分离区起始点沿展向宽度呈现中间高两边低的“山峰”型，如图11中Case 2的白色虚框所示，分离区起始点展向最大值出现在展向宽度的35%附近，而不是出现在展向中心线附近，这很可能是由于上游的吹吸扰动为展向非对称(见图2)，而这将会导致展向两侧发卡涡包大小及结构上存在差异，其最大值约为x=-14.5 mm。而起始点展向最小值出现在展向两侧，最小值约为x=-0.7 mm,这说明转捩的非线性增长阶段(Case 2)导致分离泡在展向出现了复杂的三维结构。

为了进一步直观地说明转捩的非线性增长阶段对分离泡三维结构的影响，对Case 2和Case 5情况下的分离泡瞬态形状进行了对比分析。图12 给出了Case 2和Case 5的角部干扰区内分离泡瞬态三维流向速度等值面，图中等值面取无量纲流向速度U=-0.05。该图直观地展示了分离泡的三维分布情况。可以看到，在Case 2情况下，此时分离泡的整体尺度较小，且主体结构多集中在展向中间区域，展向两侧的分离区域非常小，分离泡展向结构呈现两边低中间高的非均匀性，三维形状正如上文分析中的“山峰”型。而在Case 5情况下，此时，分离泡的整体尺度明显增大，而且分离泡的展向分布规律则与Case 2完全不同，尽管在湍流脉动的影响下，展向结构上有一定的间歇性，局部分离泡会消失，但是从整体上来看，分离泡在展向分布上均匀性较为一致，没有出现Case 2中的山峰型结构。

图11 时间平均摩阻系数展向分布 Fig.11 Spanwise distributions of time averaged skin-friction coefficient

图12 压缩拐角内瞬态分离泡的三维结构Fig.12 Instantaneous 3D representation of separation bubble at compression corner

为了更好地说明不同转捩阶段对分离泡法向高度的影响，定义如下变量[3]：

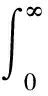
(3)

这里:

图13给出了不同转捩阶段下过拐点x=0 mm 的yOz平面内Ms沿时间的变化情况。图中横坐标t为无量纲时间，纵坐标为展向宽度，红色区域表示Ms的瞬时峰值，对应为分离泡瞬时流量峰值。该图反映了在特定x值上yOz平面内展向各点分离泡法向高度随时间演化的变化情况。要特别说明的是，由于Case 1分离区起始点已超出拐角入口，此时角部入口条件已发生改变，因此分析中只涉及Case 2～Case 5。

在DNS时，每100个无量纲时间步保存yOz平面内的瞬时流场，然后对展向各点上的u-沿法向y做积分，这样就得到了yOz平面内分离泡瞬时法向高度的变化情况。如图13中Case 2的白色虚框所示，此时分离泡瞬时法向高度峰值也出现在沿展向宽度35%附近，这与图11中Case 2的流向尺度峰值展向位置接近，而且随着时间演化，瞬时法向峰值高度的展向位置基本不变。另外，展向其他区域的分离泡瞬时高度则要低得多，这表明分离泡法向高度沿展向也呈现中间高两边低的“山峰”型，这也与图11中Case 2流向尺度的展向分布规律一致。对于Case 3～Case 5,随着时间发展，分离泡瞬时高度峰值位置展向移动的趋势逐步增强，峰值高度也呈现出逐步增大的态势，如图13中Case 5白色虚框所示。

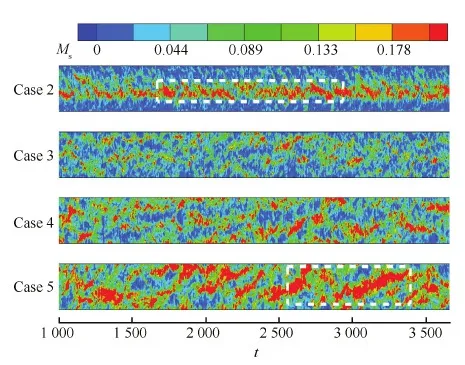
图13 x=0 mm处yOz平面内Ms随时间变化Fig.13 Time history of Ms of yOz plane at x=0 mm

3.2 湍动能分析

为了进一步考察不同转捩阶段下湍动能的变化规律与分离泡结构的关系，通过分析可压缩湍动能的输运方程，比较研究Case 2～Case 5下角部分离区内湍动能的生成、耗散和分配机制。可压缩湍动能的输运方程为[14,22]

(4)

式中：C为对流项；P为湍动能生成项；Ts为湍动能输运项；D为黏性扩散项；M为密度脉动项；Π为压力膨胀项；ε为湍动能耗散项。

角部分离区内湍动能耗散项ε的分布如图16 所示。湍动能的耗散主要集中在角部干扰区，从Case 2到Case 5，强耗散区域不断减小，但峰值位置仍出现在靠近物面的近壁区内。图17给出了干扰区内拐点x=0 mm处湍动能耗散项ε沿法向的分布情况。从Case 2到Case 5，不同转捩阶段下近壁区湍动能耗散项峰值大小下降了约4倍，湍动能耗散沿法向的分布规律基本类似，即沿物面法向往外急剧降低。

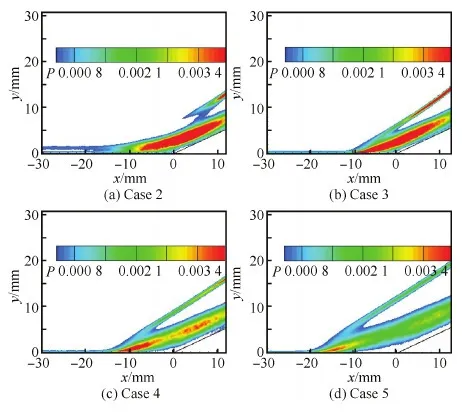
图14 角部干扰区内湍动能生成项的分布云图Fig.14 Contours of production of turbulent kinetic energy in interaction region

图15 x=0 mm处湍动能生成项沿法向分布 Fig.15 Normal distribution of production of turbulent kinetic energy at x=0 mm

图16 角部干扰区内湍动能耗散项的分布云图Fig.16 Contours of dissipation of turbulent kinetic energy in interaction region

图17 x=0 mm处湍动能耗散项沿法向分布 Fig.17 Normal distribution of dissipation of turbulent kinetic energy at x=0 mm

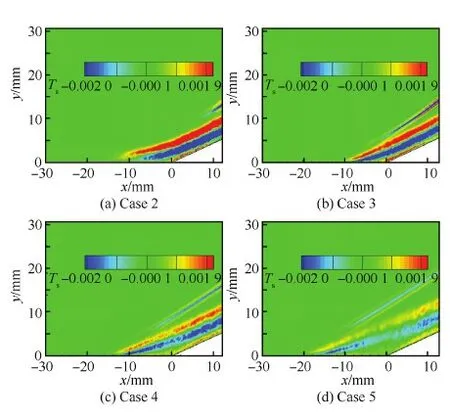
图18 角部干扰区内湍动能输运项的分布云图Fig.18 Contours of transport of turbulent kinetic energy in interaction region

图18还分别给出了Case 2～Case 5角部干扰区内湍动能输运项Ts的分布云图。图19给出了干扰区内拐点x=0 mm处湍动能输运项沿法向分布。在图18中可以看到，角部干扰区内均存在着正负排列的两层结构，此时输运项起了主要的平衡作用，将湍动能从边界层外缘输运到近壁区耗散掉。如图19所示，从Case 2到Case 5，输运项峰值大小也呈现逐渐降低的态势，但峰值位置的相对变化较小。

图19 x=0 mm处湍动能输运项沿法向分布 Fig.19 Normal distribution of transport of turbulent kinetic energy at x=0 mm

3.3 转捩影响机理初步分析

研究拟序涡结构的生成、发展及演化进程可以更深入地了解从层流转捩到湍流的发展过程及转捩的流动机理。以拟序涡结构表征的流动转捩过程，其本质上是不同尺度涡相互干扰发展的过程[15-16]。因此，为了分析边界层转捩过程中不同阶段对激波/边界层干扰分离泡的影响机理，本文采用速度梯度张量的第二不变量Q给出流场中拟序涡结构的生成及发展过程，该变量的定义具体如下[23]：

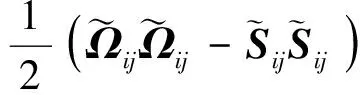
(5)

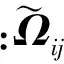
在研究转捩不同阶段对角部干扰区内分离泡影响的物理机制前，首先对超声速平板边界层Bypass型转捩的拟序结构发展过程进行了分析。图20分别给出了t=2 754(无量纲)时刻平板边界层转捩发展过程中的拟序涡结构(速度梯度张量第二不变量Q的等值面)，其中Q=0.047 9，用无量纲流向速度值0.1～1.0进行染色。从图20(a)中可以看到，在转捩初期，由于壁面周期性吹吸气作用引入的非对称局部扰动(见图2)，时空发展后在平板两侧的近壁区内出现了拟流向涡和发卡涡，如图20(a)中左上角所示。随着拟序涡结构的进一步发展，在强烈的拉伸作用下发卡涡头部区域涡量逐渐增强，而涡脚之间的展向距离进一步缩小，从而加强了自诱导作用。同时，在自诱导作用下，大尺度发卡涡附近出现了更多小尺度涡结构，并且在平板两侧逐步形成了两个发卡涡包，该涡包主要以多个大尺度的发卡涡串和流向涡组成，如图20(a)中右下角所示，这与Head和Bandyopadhyay[24]以及Lee和Wu[25-26]的研究结论是一致的。此外，从两侧发卡涡包的发展过程来看，其大小及结构与上游展向非对称的吹吸扰动存在一定的依赖关系，而且左侧涡包明显小于右侧，这也进一步验证了之前关于分离区起始点展向最大值为什么出现在展向宽度的35%附近，而不是出现在展向中心线附近的推测。

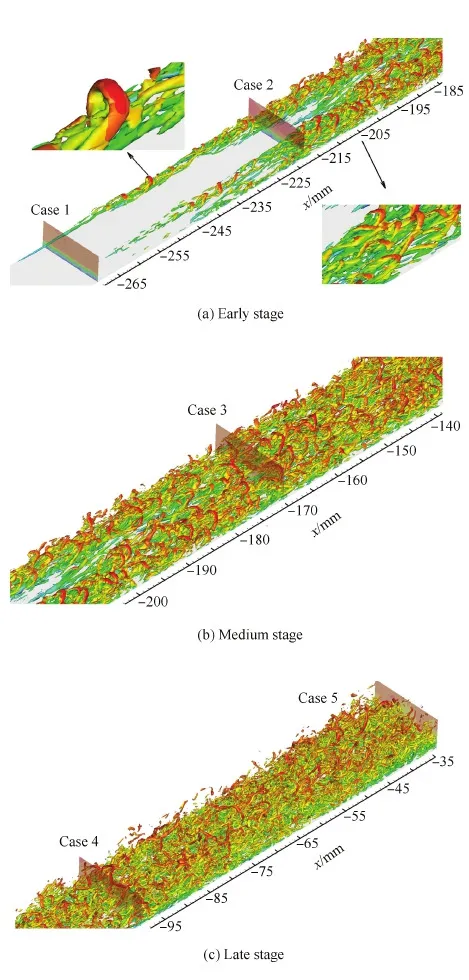
图20 t=2 754(无量纲)时刻平板边界层转捩过程拟序涡结构Fig.20 Visualization of coherent structures in transition of flat plate at t=2 754

图20(b)给出了转捩中期的流场拟序结构。此时，由于发卡涡包内强脉动流动以及周围层流区的不稳定性，两侧的发卡涡包发生相互干扰和展向融合，形成了湍流班。在转捩过程的后期，如图20(c)所示，外部高速区大尺度涡结构在强剪切层的作用下逐渐破碎成更小尺度的涡结构，同时在壁面的诱导作用下，近壁低速区内出现了越来越多的随机排列的小尺度涡结构，这表明流动已经完全转捩到了充分发展湍流阶段。图20中还分别给出了Case 1～Case 5的入口剖面对应的拟序涡结构。转捩Case 1为扰动带后转捩刚开始发生的阶段(见图4)，流场中大部分区域为层流，只是在平板一侧出现很小范围的拟流向涡。Case 2对应于平均摩阻系数{Cf}快速增长阶段，如图20(a)所示，此时的平板两侧均已经出现了较大范围的发卡涡包，发卡涡包的中间区域则为一定区域的层流。在转捩峰Case 3的情况下，两侧的发卡涡包已经发生了展向融合和法向干扰。Case 4对应于大尺度涡结构破碎和随机小尺度涡生成阶段。Case 5则为完全充分发展的湍流阶段。按照之前对平板转捩过程的分析，进一步将Case 1～Case 5划分为：Case 1和Case 2为转捩初期，Case 3为转捩中期，Case 4和Case 5为转捩后期。

图21分别给出了t=2 754(无量纲)时刻压缩拐角角部区域的拟序涡结构，这里Q=0.047 9，用无量纲流向速度值-0.4～1.0进行染色，下文类似。对于Case 1情况，由于入口处大部分区域为层流，随着流动的发展，拐角入口处仍出现了较大范围的层流，同时拐角角部内的近壁低速区以大范围的小尺度涡结构为主，大尺度的发卡涡森林则出现在外部高速区(-10 mm

图21 t=2 754(无量纲)时刻压缩拐角角部内拟序涡结构Fig.21 Visualization of coherent structures in interaction region of ramp corner at t=2 754

图21还分别给出了t=2 754(无量纲)时刻Case 3～Case 5压缩拐角角部区域的拟序结构。整体来看，从Case 3到Case 5，角部拐点上游的高速区大尺度涡结构逐渐破碎为更小尺度的结构，同时近壁低速区内随机小尺度涡结构区域不断增加，尤其是角部拐点附近的低速回流区。因此，角部分离区内高湍动能区域逐渐较少，分离泡的流向和法向尺度不断增大，这与图9和图10中Case 3～Case 5的流线分布情况及湍动能云图是一致的。

综上所述，转捩初期阶段(Case 1和Case 2)中的发卡涡森林以及展向发卡涡包结构是影响角部分离泡三维特征的主要因素。

4 结 论

本文进行了来流马赫数Ma∞=2.9，24° 压缩拐角激波/转捩边界层干扰的直接数值模拟(DNS)。在拐角上游的平板添加周期性吹吸扰动激发流动转捩到湍流，通过改变拐角上游平板的长度，使得拐角内产生激波/转捩边界层干扰。研究了转捩的不同阶段对角部干扰区分离泡尺度及形状的影响规律，结果表明:

1) 转捩对压缩拐角激波/边界层干扰分离泡结构有较大的影响。对于转捩初期，Case 1抑制住了分离泡往下游的发展，但无法抑制分离泡往上游的发展。Case 2完全抑制了分离泡的发展，分离泡尺度最小，但分离泡形状呈中间高两边低的“尖峰”型。在转捩中后期(Case 3～Case 5)，分离泡形状基本不变，但尺度有线性增大趋势。

2) Case 1的高湍动能区出现在拐角附点附近。Case 2～Case 5的峰值区域则出现在角部分离泡外，且分离泡内湍动能的生成逐步降低了约3.5倍，近壁区的湍动能耗散下降了约4倍，输运项起了主要的平衡机制，将湍动能从外层输运到近壁区耗散掉。

3) 转捩初期的拟序涡结构对分离泡结构的影响最为明显。对于Case 1，大尺度发卡涡森林出现在拐角再附点附近，抑制住了分离泡往上游的发展。而在Case 2情况下，两侧发卡涡包在角部拐点附近的展向融合和法向干扰(角部区域内湍流斑的形成)对分离泡起了展向“挤压”作用，此时分离泡尺度最小，形状呈现为中间高两边低的山峰型。

致 谢

感谢国家超级计算天津中心、中国科学院网络中心超级计算中心以及山西吕梁超算中心提供计算机时。

[1] PLOTKIN K J. Shock wave oscillation driven by turbulent boundary layer fluctuations[J]. AIAA Journal, 1975, 13(8): 1036-1040.

[2] POGGIE J, SMITS A J. Experimental evidence for plotkin model of shock unsteadiness in separated flow[J]. Physics of Fluids, 2005, 17(1): 018107.

[3] TOUBER E, SANDHAM N D. Low order stochastic modeling of low-frequency motions in reflected shock-wave boundary layer interactions[J]. Journal of Fluid Mechanics, 2011, 671(3): 417-465.

[4] DOLLING D S, MURPHY M T. Unsteadiness of the separation shock wave structure in a supersonic compression ramp flowfield[J]. AIAA Journal, 1983, 21(12): 628-634.

[5] ADAMS N A. Direct simulation of the turbulent boundary layer along a compression ramp atM=3 andReθ=1 685[J]. Journal of Fluid Mechanics, 2000, 420(3): 47-83.

[6] LOGINOV M S, ADAMS N A, ZHELTOVODOV A A. Large eddy simulation of shock wave and turbulent boundary layer interaction[J]. Journal of Fluid Mechanics, 2006, 565(1): 135-169.

[7] DOLLING D S. Fifty years of shock-wave/boundary-layer interaction research: what next?[J]. AIAA Journal, 2001, 39(8): 1517-1530.

[8] CHAPMAN D R, KUEHN D M, LARRSON H K. Investigation of separated flows in supersonic and subsonic streams with emphasis on the effect of transitions： NACA Report 1356[R]. Washington, D.C.: NASA, 1958.

[9] MURPHREE Z R, YUCEIL K B, CLEMENS N T, et al. Experimental studies of transitional boundary layer shock wave interactions: AIAA-2007-1139[R]. Reston: AIAA, 2007.

[10] VANSTONE L, SAMPER D E, HILLIER R. Shock-induced separation of transitional hypersonic boundary layers: AIAA-2015-2736[R]. Reston: AIAA, 2015.

[11] GIEPMAN R H M, SCHRIJER F F J, OUDHEUSDEN B W V. High-resolution PIV measurements of a transitional shock wave—boundary layer interaction[J]. Experiments in Fluids, 2015, 56(6): 1-20.

[12] POLIVANOV P A, SIDORENKO A A, MASLOV A A. Transition effect on shock wave/boundary layer interaction atM=1.47: AIAA-2015-1974[R]. Reston: AIAA, 2015.

[13] PRIEBE S, MARTIN M P. Low frequency unsteadiness in shock wave-turbulent boundary layer interaction[J]. Journal of Fluid Mechanics, 2012, 699(5): 1-49.

[14] LI X L, FU D X, MA Y W, et al. Direct numerical simulation of shock wave/turbulent boundary layer interaction in a supersonic compression ramp[J]. Science China: Physics, Mechanics & Astronomy, 2010, 53(9): 1651-1658.

[15] GAO H, FU D X, MA Y W, et al. Direct numerical simulation of supersonic turbulent boundary layer flow[J]. Chinese Physics Letters, 2005, 22(7): 1709-1712.

[16] LI X L, FU D X, MA Y W, et al, Acoustic calculation for supersonic turbulent boundary flow[J]. Chinese Physics Letters, 2009, 26(9): 094701.

[17] RINGUETTE M J, BOOKEY P, WYCKHAM C, et al. Experimental study of a mach 3 compression ramp interaction atReθ=2 400[J]. AIAA Journal, 2009, 47(2): 373-385.

[18] BOOKEY P, WYCKHAM C. SMITS A J, et al. New experimental data of STBLI at DNS/LES accessible Reynolds numbers: AIAA-2005-0309[R]. Reston: AIAA, 2005.

[19] WU M, MARTIN M P. Direct numerical simulation of supersonic turbulent boundary layer over a compression ramp[J]. AIAA Journal, 2007, 45(4): 879-889.

[20] MARTIN M P, TAYLOR E M, WU M, et al. A bandwidth-optimized WENO scheme for the effective direct numerical simulation of compressible turbulence[J]. Journal of Computational Physics, 2006, 220(1): 270-289.

[21] PIROZZOLI S, GRASSO F, GATSKI T B. Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer atM=2.25[J]. Physics of Fluids, 2004, 16(3): 530-545.

[22] PIROZZOLI S, BERNARDINI M. Direct numerical simulation database for impinging shock wave/turbulent boundary layer interaction[J]. AIAA Journal, 2011, 49(6): 1307-1312.

[23] JEONG J, HUSSAIN F. On the identification of a vortex[J]. Journal of Fluid Mechanics, 1995, 285(1): 69-94.

[24] HEAD M R, BANDYOPADHYAY P R. New aspects of turbulent boundary layer structure[J]. Journal of Fluid Mechanics, 1981, 107: 297-338.

[25] LEE C B, WU J Z. Transition in wall-bounded flows[J]. Applied Mechanics Reviews, 2008, 61(3): 0802.

[26] LEE C B. Possible universal transitional scenario in a flat plate boundary layer: measurement and visualization[J]. Physical Review E, 2000, 62(3): 297-338.

童福林男， 博士研究生， 助理研究员。主要研究方向： 可压缩湍流直接数值模拟， 高超声速气动热和热防护。

Tel: 0816-2463133

E-mail: wowo2020@sohu.com

唐志共男， 博士， 研究员， 博士生导师。主要研究方向： 高超声速空气动力学。

Tel: 0816-2463133

E-mail: 515363491@qq.com

URL：www.cnki.net/KCMS/detail/11.1929.V.20160125.1638.008.html

Transitioneffectonseparationbubbleofshockwave/boundarylayerinteractioninacompressionramp

TONGFulin1,LIXinliang2,TANGZhigong1,*,ZHUXingkun2,HUANGJiangtao1

1.ComputationalAerodynamicsInstituteofChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China2.KeyLaboratoryofHighTemperatureGasDynamics,InstituteofMechanics,ChineseAcademyofSciences,Beijing100190,China

Directnumericalsimulations(DNS)ofshockwaveandtransitionalboundarylayerinteractionfora24°compressioncorneratMachnumber2.9areperformedtostudytheeffectoftransitionontheseparationbubbleattherampcorner.Atupstream,theflat-platetransitionistriggeredbytheperiodicblowandsuctiondisturbance.Theinteractionofshockwaveandtransitionalboundarylayeristhensimulatedbysettingthelengthofupstreamflat-plate.Theextentofseparationagreeswellwiththoseoftheexperimentalanddirectnumericalsimulationdata,whichvalidatetheresults.Transitioneffectontheseparationbubbleintheinteractionregionisresearchedandtheturbulentkineticenergybudgetinthebubbleisanalyzed.Resultsindicatethatthecoherentstructuresattheearlystageoftransitionhaveaseriousinfluenceontheseparationbubble,inwhichtheturbulentspotsareformedbythehairpinvortices.Thenthescaleofseparationbubbleisthesmallestandtheshapeisspike-typeinthespanwisedirection.Withtheevolutionoftransition,theturbulentproductionanddissipationtermintheseparationbubblegraduallyreducebyfourtimes,whiletheturbulenttransporttermcontributestothebalanceoftheturbulentproductionanddissipation.

transition;compressionramp;shockwave/boundarylayerinteraction;separationbubble;directnumericalsimulation

2015-10-23；Revised2015-12-08；Accepted2015-12-20；Publishedonline2016-01-251638

s：NationalNaturalScienceFoundationofChina(91441103,11372330)

.Tel.：0816-2463133E-mail515363491@qq.com

2015-10-23；退修日期2015-12-08；录用日期2015-12-20； < class="emphasis_bold">网络出版时间

时间：2016-01-251638

www.cnki.net/KCMS/detail/11.1929.V.20160125.1638.008.html

国家自然科学基金 (91441103,11372330)

.Tel.：0816-2463133E-mail515363491@qq.com

童福林， 李新亮， 唐志共， 等． 转捩对压缩拐角激波/边界层干扰分离泡的影响J． 航空学报,2016,37(10):2909-2921.TONGFL,LIXL,TANGZG,etal.Transitioneffectonseparationbubbleofshockwave/boundarylayerinteractionsinacompressionrampJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):2909-2921.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0355

V211.3； O354.3

A

1000-6893(2016)10-2909-13