埃博拉病毒传播模型及规律预测

褚雨薇 管祥善 刘琦 王煜凯

摘要：埃博拉病毒是一种能引起人类和灵长类动物产生埃博拉出血热的烈性传染病病毒。文章以2014年西非疫区为参照，建立虚拟环境的常微分方程组，利用四阶龙格—库塔法求解其数值解，具体通过C语言程序设计实现，并据此研究埃博拉病毒的传播规律，分析隔离措施的严格执行和药物治疗效果的提高等措施对控制疫情的作用。

关键词：数学建模;埃博拉病毒;常微分方程组数值解;四阶龙格—库塔法;西非疫区 文献标识码：A

中图分类号：O175 文章编号：1009-2374（2016）04-0194-03 DOI：10.13535/j.cnki.11-4406/n.2016.04.096

1 模拟真实环境

埃博拉病毒的自然宿主虽尚未最后确定，但已有多方证据表明猴子及猩猩等野生非人灵长类动物有埃博拉感染现象。该病毒的传播途径分为人畜传播、人人传播两种。2014年，在几内亚、塞拉利昂和利比里亚等国，许多受埃博拉病毒影响的人口都以丛林肉为重要的蛋白质和营养物质来源，与丛林中动物接触频繁。这为人畜之间的病毒传播创造了条件。

我们现假设两个感染埃博拉病毒的虚拟种群：即某地区内的20万居民和3000只猩猩。人能以一定的概率接触到所有的猩猩，当接触到有传播能力的猩猩后有一定概率感染病毒，而人发病之后与猩猩的接触可以忽略。人与猩猩的潜伏期都为2周。并在出现疫情41周后模拟外界医疗力量的介入，使得人类与猩猩不再发生接触，且隔离治疗人群的治愈率提高到80%。模拟数据详见附录。

2 建立数学模型

2.1 模型假设

（1）依据人或猩猩的健康状态，将人或猩猩划分为健康者、埃博拉感染者（也称患病者）、退出者（含自愈者、死亡者）;（2）自然封闭条件下，猩猩无自然迁移，故无病源的流入、流出，种群数量不变。人类数量庞大，在无大规模迁移的情况下，认为人类数目为一定值，保持不变;（3）健康者中不包含退出者;（4）人和猩猩自愈后二度感染的概率均为0，人被治愈后二度感染的几率为0;（5）不存在有效免疫药物可使人对埃博拉病毒产生免疫，同时猩猩对病毒也不免疫;（6）人的传染途径有人传染人、猩猩传染人两条。两条途径的传染率并不相同，分别假设为传染率C1和传染率C2。C1猩猩与猩猩之间传染途径只有猩猩传染猩猩一条，假设猩猩之间的传染率为C0;（7）患病人无法传染患病猩猩;（8）41周外界介入后，猩猩与人的传播途径切断，隔离患者的治愈率提高到80%，同时未被隔离的患者治愈率不变。

2.2 符号说明

符号说明如表1所示：

3 模型的建立与求解

3.1 数据处理

根据累计死亡个体数，求得每周死亡个体数。同理，根据累计自愈个体数，求得每周自愈个体数。由每周仍处于发病状态的个体数加本周自愈个体数和本周死亡个体数得到每周总患病个体数。

由每周总患病个体数比总体数目得到每周患病个体在总体中的比例A（t）;由相邻两周每周患病数相减得到每周新增患病数。由总体个数减去新增病例累计和获得健康个体数，并由此得到健康个体在总体中的比例J（t）;由累加自愈治愈人数与累加死亡人数得到退出者总数量，并由此得到退出者在总体中的比例T（t）。

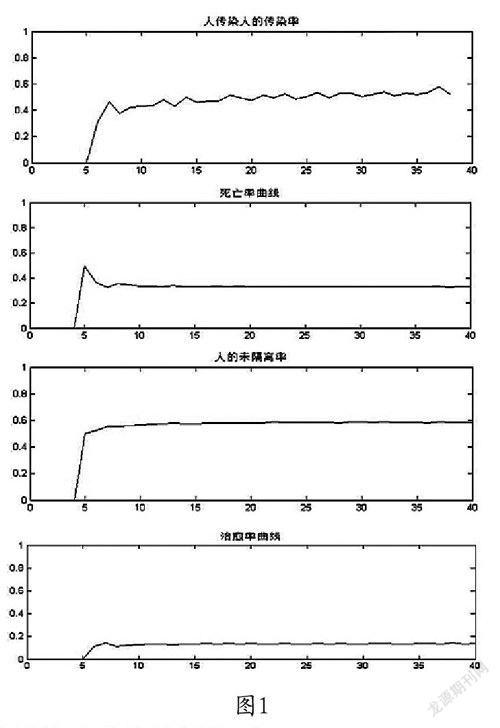
由于埃博拉病毒的潜伏期是两周，所以任意一周的新增病例是两周前处于患病状态的个体传染的。由新增病例数比两周前处于患病状态的个体数得到该周埃博拉病毒传染率，由此计算出每一周的传染率。通过MATLAB绘图，我们得到其近似曲线为一条平行于X轴的曲线，所以通过加权平均求得平均传染率。

因为人类最初患病个体不可能为人类传染所致，所以两周内出现的患病者必为由猩猩传播而来的。最初两周，人每周新增的患病个数除以处于两周前患病状态的猩猩个数得到猩猩与人之间平均传染率C1。

两周之后人患病可由猩猩和人传播两种途径导致，猩猩每周处于患病状态的数量和C1已知，所以每周由猩猩传播导致人患病的数量可求出，用每周新增患病人数减去每周猩猩传播导致人患病的数量，即每周由人传染导致的患病数量。由每周人传染导致的患病数量除以两周前未被隔离处于患病状态的人数可得到每周埃博拉人与人之间传染率C1，通过MATLAB画出C2的图像，可以发现其图像为平行于x轴的曲线，可通过加权平均求出人与人之间平均传染率C2。

死亡率是由本周死亡个数比本周总病例数得到。我们由此求得每一周的死亡率。通过MATLAB绘图我们得到一条同样近似平行于X轴的曲线，所以通过加权平均，求得疫情稳定后平均死亡率。

每周处于未隔离的患者人数处于每周的处于患病状态的总人数可得到每周的未隔离率G，其图像为平行于x轴的曲线，通过加权平均求出平均未隔离率G。

同理，我们还得到疫情稳定后的平均自愈及治愈率。我们近似地认为，在病情爆发后不久，即疫情稳定后，周感染率、周死亡率、周治愈自愈率、周未隔离率都是常值。

3.2 埃博拉病毒的传播模型

由假设知，猩猩患病只能由猩猩传播。每个患病猩猩每周可使得只的健康猩猩变为患病猩猩，由患病猩猩数量得每周共有只健康猩猩被感染。即患病猩猩的增加率，又因为每周自愈的猩猩数目为，死亡的猩猩数目为，所以猩猩患病数随时间变化满足：

同理，我们得到人类的传播模型（由前述，所有脚标为2的符号均为人类相关数据，脚标为1的符号为与猩猩相关数据）：

3.3 模型求解

通过联立方程组和数据处理，我们使用四阶龙格—库塔法分别求出人和猩猩群体中健康者和患病者的比例的数值解。

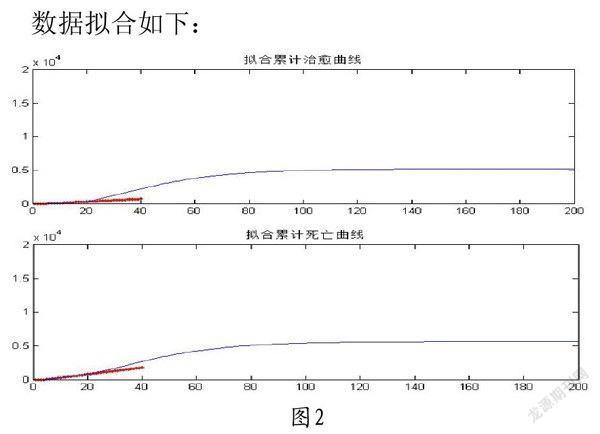
通过C程序设计编译程序求解模型所用常微分方程组的数值解。该程序在前四十组解得检验中拟合程度极高，故由此得到较为可靠的预测数据。C语言程序代码详见附录。

数据拟合如下：

3.4 建立使用免疫药物后的模型

未被隔离患者的治愈率和被隔离患者的治愈率加权平均后得到患者的平均治愈率Zh。1-Zh为死亡率与未被治愈率之和。默认死亡率与未被治愈率权重不变。在（1-Zh）中，可以算出死亡率的权重和未被治愈率的权重。在严格控制人类与黑猩猩接触并使用特效药后的数学模型如下：

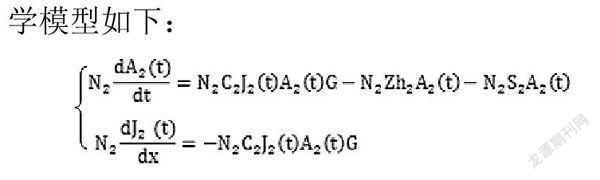
将之与隔离前模型对照后发现，特效防疫药物的使用极大地提高了治愈率Zh，快速地降低了患病数。而隔离黑猩猩的措施将黑猩猩传染致病人数降为0。

综上，两种措施都有效地预防了疾病的进一步扩散，抑制了疾病的传播，使患病人数的增长率由正变负，从而导致患病数在短期内大量且持续减少。

4 模型的评价与推广

4.1 模型优势

（1）种群数量较小时，通过求解比例的变化得出结果较为精确;（2）可以动态地描述种群发病率、死亡率、自愈率、治愈率、传染率等多种特征量;（3）四阶龙格—库塔法通过数值求解常微分方程组，很好地拟合了给定的原始数据。

4.2 模型缺陷

（1）由于通过比例而非数量求解，所以当种群数量较大且比例变化不明显时误差较大;（2）认为两个“虚拟种群”内部个体总数在随时间变化时基本不变，未考虑个体总数的时间变化率。

5 附录

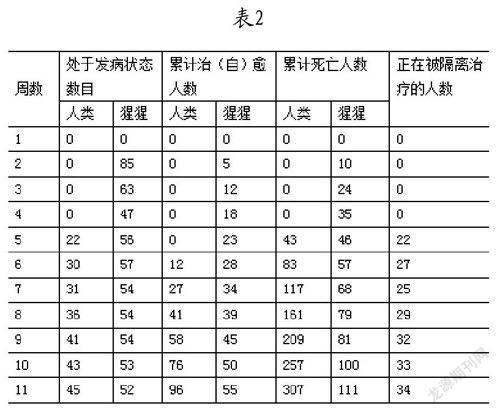
5.1 模拟数据

模拟数据如表2所示：

5.2 C语言程序代码

参考文献

[1] 李信真.计算方法[M].西安：西北工业大学出版社，2013.

[2] H.Nishiura，G.Chowell.EARLY TRANSMISSION DYNAMICS OF EBOLA VIRUS DISEASE（EVD）[J].WEST AFRICA，2014，（8）.

[3] 甄西丰.实用数值计算方法[M].北京：清华大学出版社，2006.

[4] 刘来福，何青.用Maple和MATLAB解决科学计算问题[M].北京：高等教育出版社，1999.

（责任编辑：王 波）