高强高性能混凝土损伤的细观数值演化
郑 捷, 左河山, 陈景恒, 曹文平, 郑山锁
(西安建筑科技大学 建筑设计研究院,陕西 西安 710055)
高强高性能混凝土损伤的细观数值演化
郑 捷, 左河山, 陈景恒, 曹文平, 郑山锁
(西安建筑科技大学 建筑设计研究院,陕西 西安 710055)
在细观层次上,混凝土可以被看作由水泥基、分散粒子和界面过渡层组成的三相复合材料。首先,基于骨料分布和形态的随机特性,将瓦拉文公式推广应用于确定二维混凝土试件截面凸多边形骨料分布,提出圆形骨料模型中以圆骨料的面积为控制参数,以圆内接多边形为基架的凸多边形随机骨料算法。进而以C80高强高性能混凝土为例,对数值试样进行单轴受压的数值模拟,得到相应的应力-应变曲线和损伤演化图。数值模拟结果与物理试验结果对比表明本文提出的数值模型合理可行。
高强高性能混凝土; 随机骨料模型; 细观数值模拟; 损伤演化; 损伤有限元
0 引言
已有描述混凝土断裂损伤的细观模型,如格构模型、随机粒子模型、随机骨料模型等,都是针对普通混凝土,并假定混凝土是由砂浆基质、骨料和二者之间的黏结带组成的三相复合材料,从而采用细观层次上的简单本构关系来模拟材料复杂的宏观断裂过程[1-3]。
本文借鉴普通混凝土的细观层次研究思路,对高强高性能混凝土(HSHPC)的细观结构进行合理的简化,运用MATLAB软件建立随机骨料模型,基于损伤有限元分析方法,利用APDL语言编译损伤有限元计算程序,生成可进行数值试验的“高强高性能混凝土数值试样”并进行数值计算,将计算结果与课题组前期所获得的试验数据对比,以验证数值模型的准确性[4-6]。
1 随机骨料模型的建立
1.1 骨料粒径的计算
三维富勒级配曲线和工程中常用的级配曲线吻合较好[7],然而空间的模拟计算量十分巨大。瓦拉文(Walraven J.C.)公式[8]建立了混凝土试件空间内骨料级配及含量与其截面所切割的骨料面积的关系,使得混凝土细观分析能够在二维平面内进行,从而大大减少了计算量:
(1)
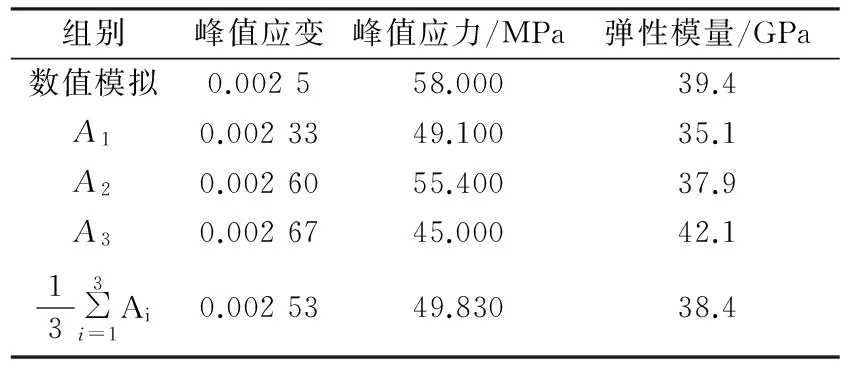
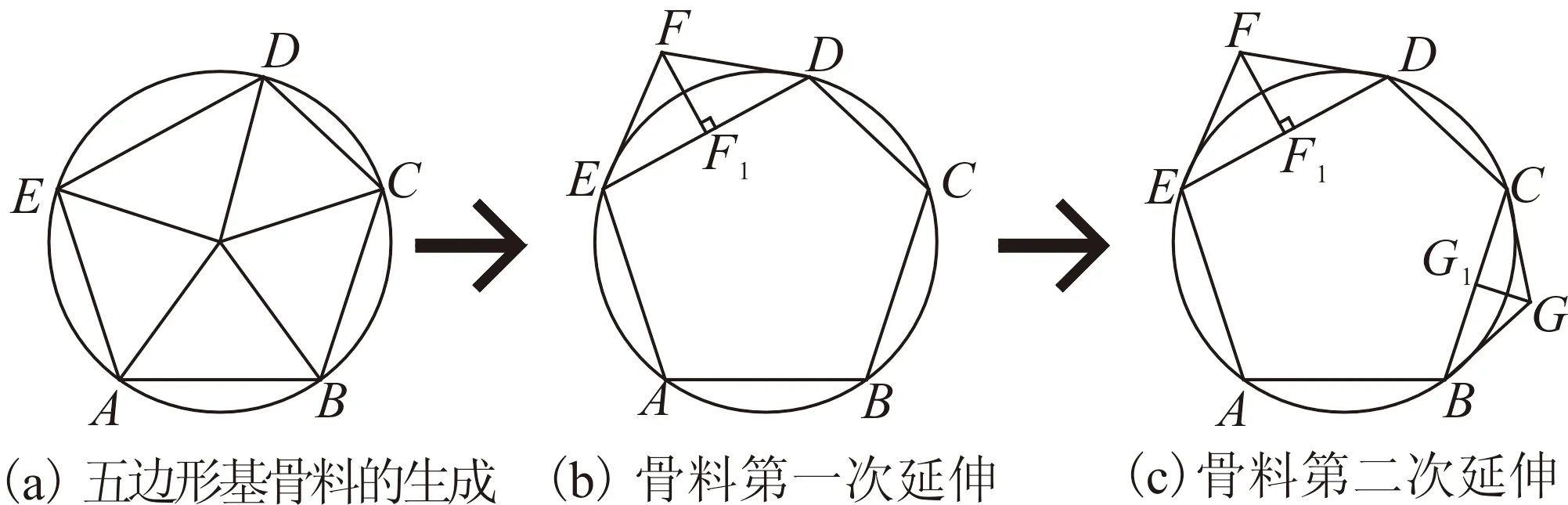
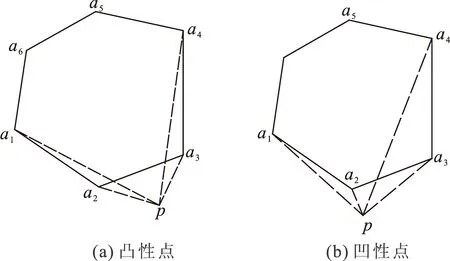
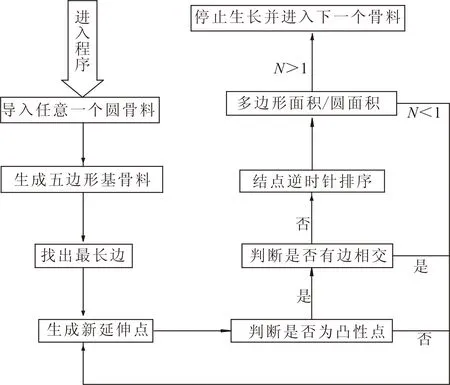
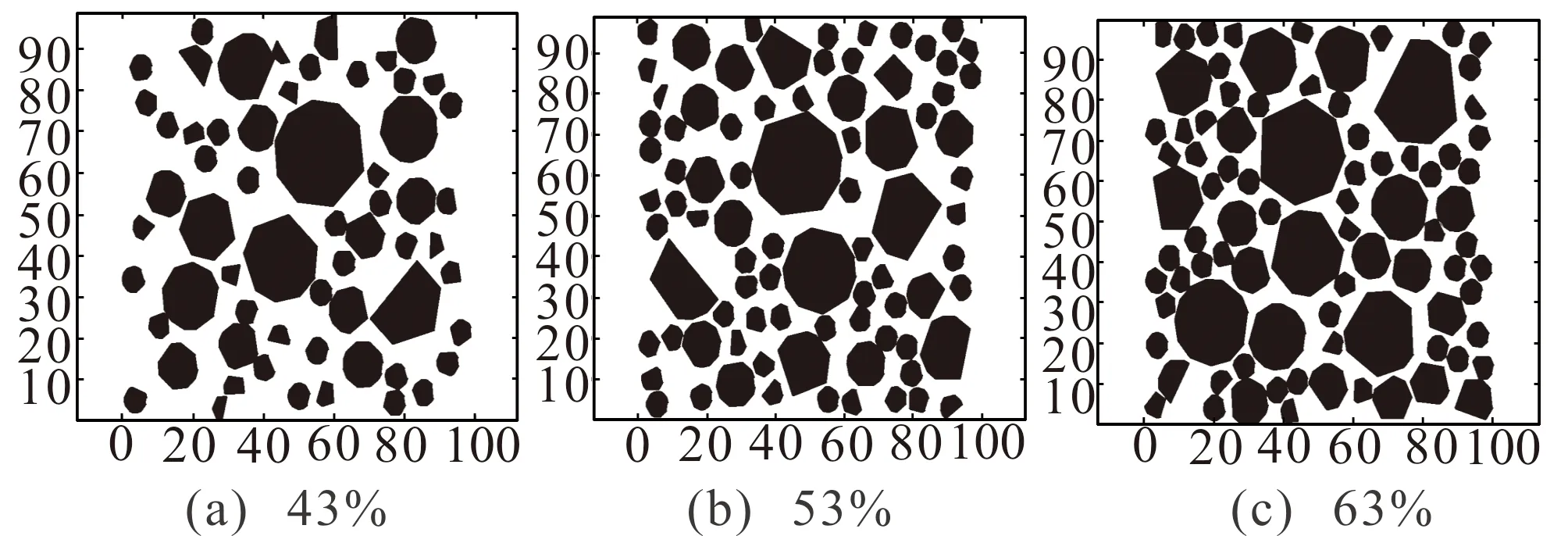
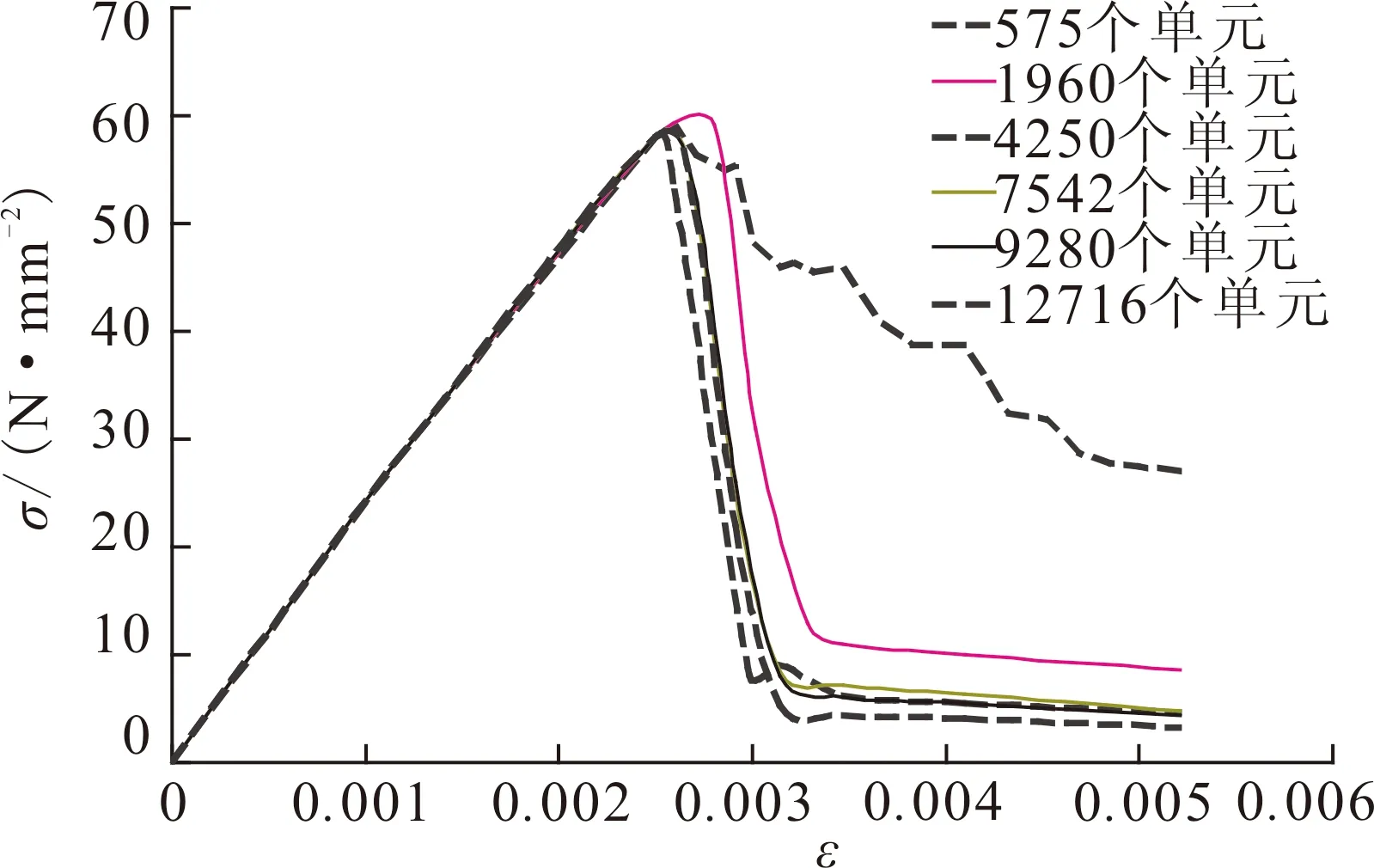
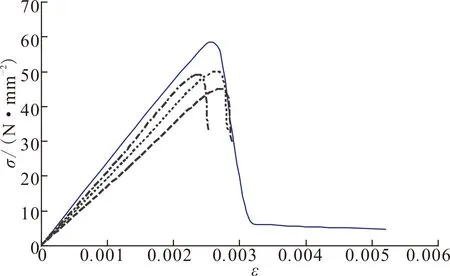
式中:Pk为粗骨料和细骨料体积之和与混凝土总体积之比,取值范围在0.6~0.8之间;Pc(D 根据瓦拉文公式,将三维富勒骨料级配曲线转化为二维骨料级配曲线,从而可以确定填充区域内不同粒径的骨料颗粒数Ni: (2) 式中:A为试件的截面积;Ai为该骨料的截面面积。 1.2 圆形随机骨料模型生成算法 首先确定混凝土试件的平面范围,然后在其平面内利用MATLAB软件RAND函数随机确定骨料的圆心位置。圆形骨料可以通过圆的直径和圆心坐标值(x,y)确定。值得注意的是,当一个新骨料产生时必须确定该骨料和先前骨料之间不会出现位置的重叠或交叉,还需保证该骨料在混凝土试件平面之内。 将上述投放流程由MATLAB进行实现,得到100mm×100mm矩形框内的混凝土二维圆形随机骨料分布模型,骨料含量分别为43%[图1(a)]、53%[图1(b)]和63%[图1(c)]。 图1 圆形随机骨料模型Fig.1 Cricular random aggregate model 1.3 多边形随机骨料模型生成算法 已有二维任意形状骨料的投放算法生成骨料的速度太慢[9-10],本文在文献[10]的基础上做了改进,以提高骨料的生成效率,并使得数值模拟的骨料更加符合真实骨料形状。对算法的改进包括: (1) 基骨料从三角形变为五边形,五边形决定了最终生成骨料的粒径和形状趋势。与三角形相比,五边形具有面积大、形状饱满、更容易达到投放面积的优点。多次程序调试与运行表明,五边形比三角形更有利于加快程序运行效率。 (2) 凸多边形判断时,对于“非凸性点”,程序不采用“剔除法”,而采用“替代法”。“替代法”的优势在于避免重新生成新点,减少了运算量。实践证明算法改进后程序运行效率有了显著地提高。 1.3.1 生成随机五边形基骨料 在圆形骨料基础上,把圆平均分成五段圆弧,在每段圆弧上随机生成一个点,连接生成五边形ABCDE(按照逆时针方向),如图2(a)所示。 图2 五边形生成任意多边形骨料过程Fig.2 Process from pentagon to general polygon aggregate 1.3.2 骨料延伸方式 Step1:在五边形ABCDE上计算各个边长,选取最长的边,假设为DE,如图2(a)所示; Step2:作DE的中垂线得到FF1,并使得Kmax>FF1>Kmin(Kmax和Kmin为常数),连结DF、EF形成新的边,此为骨料的第一次延伸,如图2(b)所示。在延伸过程中,中垂线上点F应在五边形形成面域之外选取,骨料延伸方式遵循凸多边形侵入准则和判定准则; Step3:在六边形ABCDFE上计算各个边长,选取最长的边,假设为BC,并按照Step2的方法生成新的点G,此为骨料的第二次延伸,如图2(c)所示; Step4:重复Step2和Step3,生成新的多边形; Step5:当新生成的多边形骨料面积所占圆面积百分比高于N(N为常数),该骨料即停止生长,并进行下一个骨料的生成。 1.3.3 凸多边形判定及“替代法” 真实世界的碎石一般为凸多边形。在骨料生成过程中,如何保证生成的多边形为凸多边形是关键的一步。对于凸多边形和凹多边形的判断可以从三角形面积正负入手。如图3所示,p为多边形边a2a3上方的顶点(延伸点),如果p与边a2a3邻边a3a4、a1a2连成的三角形Δpa1a2、Δpa2a3按照式(3)算得的面积均为正,则点p为“凸性点”;如果p与边a2a3邻边a3a4、a1a2连成的三角形Δpa1a2、Δpa2a3按照式(3)算得的面积不全是正值,则点p为“凹性点”。所以图3(a)中的p点为“凸性点”,图3(b)中的p点为“凹性点”。 图3 凸性点判别Fig.3 Judgment of the convex point (3) 式中:(xi,yi)、(xi+1,yi+1)分别为图3所示凸多边形顶点ai和ai+1的坐标;(x,y)为图3所示凸多边形平面内任一点p的坐标;S为图3中所连成的三角形Δpaiai+1(i=1,2,…1)的面积,其正负值由p、ai、ai+1的排列顺序决定:若三个点按逆时针排列,则S为正,若三个点按顺时针排列,则S为负。 对于图3(b)的“凹性点”p,如果根据传统的“剔除法”直接剔除并重新生成,将耗费较多的CPU资源,且程序的运行速度也会大打折扣。本文提出“替代法”,具体为:直接连接点p和点a1,用点p替代点a2,这样多边形由a1a2a3a4a5a6变为a1pa3a4a5a6,多边形的边长数量未变,但面积增大了(Spa2a3、Spa1a2)。这种改进的算法有利于避免形成“凹多边形”,还能加快多边形的生成以满足面积要求,从而提高了生成效率。 单个骨料的生成程序流程见图4。投放流程由MATLAB进行实现,得到100 mm×100 mm矩形框内的混凝土二维多边形随机骨料分布模型(图5),骨料含量分别为43%[图5(a)]、53%[图5(b)]和63%[图5(c)]。 图5中所生成多边形骨料和实际的碎石骨料比较相似,且分布较均匀,从而证明了算法的正确性与可靠性。 图4 多边形随机骨料投放程序基本流程Fig.4 The basic process of delivery program for polygon random aggregate 图5 任意多边形骨料模型Fig.5 General polygon aggregate model 2.1 高强高性能混凝土细观结构的简化 对于普通混凝土,骨料-硬化砂浆界面通常被认为是其材料性能发展的薄弱环节,而本研究中用于型钢混凝土组合结构的高强高性能混凝土,由水泥、粗骨料、细骨料、水、活性矿物掺合料以及高效外加剂组成,且课题组对配合比进行了优化设计[4-6],高强高性能混凝土在达到强度的90%~95%时才会出现开裂现象,而在这之前基本没有黏结裂缝出现,骨料与水泥砂浆具有更高的黏结强度,使得HSHPC中骨料与水泥砂浆在整个受力过程中基本能够共同工作。因此本文假设混凝土组成成分中骨料和砂浆能协同工作,忽略骨料-砂浆界面层对模型的影响,高强高性能混凝土细观模型被简化为由骨料单元和硬化水泥砂浆单元组成。 2.2 细观材料本构模型 本文在分析混凝土细观尺度的变形、损伤和破坏过程中认为混凝土是一种准脆性材料[12],其受力后在宏观上呈现应力-应变曲线的非线性是由于受力后不断损伤引起裂纹萌生和扩展造成的,而不是由于其塑性变形引起的。基于此,弹性损伤力学的本构关系可以用来描述混凝土的细观单元各相的力学性质。 本文中损伤阀值应用最大拉应变准则表示。该准则认为当细观单元的最大拉伸主应变达到给定的极限值时,该单元开始发生拉伸损伤。细观单元的弹性损伤本构关系如图6所示。 对于图6所给出的本构曲线,损伤变量的表达式[10]为 (4) 式中:ft为混凝土试样各组分的抗拉强度;ftr为各相破坏单元的抗拉残余强度,ftr=λft,λ为残余强度系数,0<λ≤1;εt0为单元应力达到抗拉强度时的主拉应变;εtr为与抗拉残余强度相对应的残余应变,εtr=ηεt0,η为残余应变系数,对于混凝土试样各组分,1<η≤5;εtu为极限拉应变,εtu=ξεt0,ξ为极限应变系数,ξ>η;εmax为单元加载历史上主拉应变的最大值。依据课题组前期试验数据[4-6],各参数的数值见表1。 表 1 高强高性能混凝土细观单元力学参数 2.3 计算实例 以C80高强高性能混凝土立方体试件为例(截面尺寸为100 mm×100 mm)模拟其在单轴受压载荷作用下的力学行为,并与相应物理试验对比,以验证随机骨料模型的正确性。 2.3.1 骨料颗粒的计算 依据高强高性能混凝土配合比实验[4-6],粗骨料代表粒径分别为27.5、22.5、17.5和12.5 mm,粒径分布满足富勒级配曲线,最大骨料粒径为30 mm。高强高性能混凝土试验配合比数据见表2。 表 2 C80混凝土试验配合比(单位:kg/m3) 根据瓦拉文公式可计算得到C80高强高性能混凝土粗骨料颗粒数如表3所列[4-6]。 表 3 C80混凝土粗骨料颗粒数 2.3.2 有限元网格剖分 通过MATLAB软件建立高强高性能混凝土随机骨料几何模型,利用AUTOCAD的纽带作用,将几何模型导入至ANSYS,以形成APDL语言,并对其进行改进和完善。对几何模型进行有限元网格划分,为使结果更好地收敛,骨料平面采用映射网格划分技术;砂浆平面为极不规整平面,利用映射划分技术根本无法形成可以计算的网格,故采用自由网格划分技术。高强高性能混凝土平面试样有限元模型如图7所示,其单元总数为9 280。 图7 高强高性能混凝土平面试样有限元模型Fig.7 Finite element model of HSHPC specimens 2.3.3 HSHPC单轴受压过程数值模拟 根据弹性损伤本构关系,将高强高性能混凝土各相组分的力学参数(表1)分配给有限元模型中相应的细观单元,得到混凝土材料数值试样,并对该试样进行单轴受压数值模拟(加载方式以及边界条件见图8,底部节点横向自由度全部约束住,顶部节点施加一个位移荷载)。为避免产生刚体位移,将底部坐标为(0,0)的节点纵向自由度约束住。 图8 单轴受压数值试验加载及约束Fig.8 Loading mode and constraint under uniaxial compression numerical test 图9为HSHPC单轴受压应力-应变曲线。可以看出,曲线的上升段基本为直线,表明在数值模拟中上升段的细观单元很少发生损伤。当应力达到峰值后曲线骤然下跌,表现出明显的脆性,作者认为原因有两个:(1)砂浆单元和骨料单元的抗拉强度、泊松比及弹性模量等力学性质相近导致单元损伤或破坏几乎同时发生,从而导致试件的刚度矩阵急剧下降;(2)骨料单元产生了损伤和破坏,裂缝的发展不再受到骨料的制约,应力-应变曲线迅速回落,形成陡峭的尖峰,应力-应变曲线形成的面积明显减小。 图9 HSHPC单轴受压过程应力-应变曲线Fig.9 Stress-strain curves of HSHPC under uniaxial compression 图10为HSHPC单轴受压细观单元损伤演化图。高强高性能混凝土试件在大部分时候处于弹性状态,损伤单元和黏结裂缝非常少;当达到开裂临界应力(第190荷载步)时损伤单元突然大面积出现,当达到峰值应力时破坏单元开始大面积出现,其在受拉和受压数值模拟中均存在骨料单元破坏,且破坏主裂缝均穿过骨料,这与高强高性能混凝土中骨料和基体的强度相近,甚至基体的强度高于骨料,骨料已经成为HSHPC薄弱环节的结论是一致的[4];最后形成从上至下的宏观主裂缝,倾角大概在70°。 图10 HSHPC单轴受压细观单元损伤演化图Fig.10 Damage evolution of mesoscopic units of HSHPC under uniaxial compression 2.3.4 单元数目的影响 以上分析都是针对单元数目为9 280的试样进行的。本小节研究当模型尺寸相同而单元数目不同时分析结果的差别。图11给出了不同单元数模型立方体试样的应力-应变曲线。 图11 单元数目对数值试样应力-应变曲线的影响Fig. 11 Effect of unit number on stress-strain curves of specimens 由图11可知,减少单元数目将提高数值试样应力-应变曲线的韧性,而降低其脆性;增加单元数目将降低其韧性,而提高其脆性。这一现象与普通混凝土数值模拟结果类似[11]。究其原因,单元的数目基本不影响数值试样的峰值强度和初始弹性,但增加单元数目会提高总体的均匀性。 2.3.5 试验验证 由图12可知,对于应力-应变曲线上升段,数值模拟结果与试验结果吻合较好,但数值模拟的弹性模量和峰值应力较试验数值高,这是因为在数值模拟中没有考虑初始损伤;对于曲线下降段,由于高强高性能混凝土的脆性性质和试验机的刚度不足等原因使得下降段只能得到一部分,故下降段无法比较。由表4可知[4-6],数值模拟结果(包括峰值应变、弹性模量等)均处在三组试验结果范围内,表明本文建立的细观数值模型能较好地模拟高强高性能混凝土的单轴受压力学行为。 图12 数值模拟结果与试验结果对比(应力-应变曲线)Fig.12 Comparison between simulation results and test results (stress-strain curves) (1) 基于骨料形态和分布的离散特点,将瓦拉文公式应用于确定二维混凝土试件截面粗骨料的分布,提出以圆形随机骨料模型中圆骨料的面积为控制参数,以圆内接五边形为基架的凸多边形随机骨料算法。凸多边形骨料分布的骨料颗粒级配及其在试件截面内的面积与圆形骨料均相同。 表 4 数值模拟结果与试验结果对比 (2) 建立点与多边形及多边形与多边形的贯穿和侵入的几何关系,分别利用MATLAB语言和APDL语言编制随机骨料模型生成程序和损伤有限元计算程序。通过C80高强高性能混凝土单轴受压数值模拟的计算实例验证本文建立的数值模型的正确性。 (3) 数值模型中仅仅模拟了骨料分布的随机性,没有考虑混凝土各相力学特性参数在计算域内的随机分布,故材料发生破坏的荷载水平较试验高。 (4) 本文建立的损伤本构模型仅适用于单元压伸情况,而在混凝土发生单轴受拉过程中,极少数单元会发生剪切损伤破坏,这方面本构模型的选取需要基于有关试验结果的观察分析得出。 References) [1] Wittmann F H,Roelfstra P E,Sadouki H.Simulation and Analysis of Composite Structures[J]. Materials Science and Engineering,1985,68(2): 239-248. [2] Sadouki H S,Wittmann F H.On the Analysis of the Failure Process in Composite Materials by Numerical Simulation[J].Materials Science & Engineering A:Structural Materials:Properties,Microstructure and Processing,1988,A104:9-20. [3] 马怀化,陈厚群,黎保琨.混凝土细观力学研究进展及评述[J].中国水利水电科学研究院学报,2004,2(2):124-130. MA Huai-hua,CHEN Hou-qun,LI Bao-kun.Review on Micro-mechanics Studies of Concrete[J].Journal of China Institute of Water Resources and Hydropower Research,2004,2(2):124-130.(in Chinese) [4] 郑捷,左河山,李文博,等.设计因素对RC框架结构地震易损性的影[J].地震工程学报,2016,38(4):1-8. ZHENG Jie,ZUO He-shan,LI Wen-bo,et al.Influence of Design Factors on Seismic Fragility of RC Frame Structures[J].China Earthquake Engineering Journal,2016,38(4):1-8.(in Chinese)[5] 邓国专.型钢高强高性能混凝土结构力学性能及抗震设计的研究[D].西安:西安建筑科技大学,2008. DENG Guo-zhuan.Mechanical Behaviors and Seismic Design of Steel Reinforced High Strength High Performance Concrete Composite Structures[D].Xi’an:Xi’an University of Architecture and Technology,2008.(in Chinese) [6] 郑山锁,马德龙,刘洪珠.汶川地区震后钢筋混凝土框架结构的地震易损性研究[J].地震工程学报,2015,37(1):131-137. ZHENG Shan-suo,MA De-long,LIU Hong-zhu.Seismic Vulnerability of Post-earthquake Reinforced Concrete Frame Structures in the Wenchuan Area[J].China Earthquake Engineering Journal,2015,37(1):131-137.(in Chinese) [7] 马怀发,陈厚群,黎保琨.混凝土试件细观结构的数值模拟[J].水利学报,2004(10):1-10. MA Huai-fa,CHEN Hou-qun,LI Bao-kun.Meso-structure Numerical Simulation of Concrete Specimens[J].Journal of Hydraulic Engineering,2004(10):1-10.(in Chinese) [8] Walraven J C,Reinhardt H W,Theory and Experiments on the Mechanieal Behavior of Cracks In Plain and Reforced Concrete Subject to Shear Loading[J].HERON,1991,26(1A):26-35. [9] Wang Z M,Kwan A K H,Chan H C.Mesocopic Study of Concrete I:Generation of Random Aggregate Structure and Finite Element Mesh[J].Computers and Structures,1999,70:533-544. [10] 高政国,刘光廷.二维混凝土随机骨料模型研究[J].清华大学学报:自然科学版,2003,43(5):710-714. GAO Zheng-guo,LIU Guang-ting.Two-dimensional Random Aggregate Structure for Concrete[J].J Tsinghua Uni:Sci & Techn,2003,43(5):710-714.(in Chinese) [11] 唐春安,朱万成.混凝土损伤与断裂——数值试验[M].北京:科学出版社,2003. TANG Chun-an,ZHU Wan-cheng.Damage and Fracture of Concrete——Numerical Simulation[M].Beijing: Science Press,2003.(in Chinese) [12] Berthelot J M,Robert J L.Damage Evaluation of Concrete Test Speciments Related to Failure Analysis[J].Journal of Engineering Mechanics,ASCE,116(3):587-604. Meso-scale Numerical Analysis of Damage Evolution of High-strength and High-performance Concrete ZHENG Jie, ZUO He-shan, CAO Wen-ping, CHEN Jing-heng, ZHENG Shan-suo (ArchitecturalDesign&ResearchInstitute,Xi'anUniversityofArchitectureandTechnology,Xi'an710055,Shaanxi,China) On a meso-level, concrete can be seen as a three-phase composite material comprising a cement base, aggregate, and a transitional zone between the cement and aggregate. In this study, based on the random characteristics of the aggregate distribution and morphology, the Walraven formula is applied to determine the convex polygonal aggregate distribution of the two-dimensional concrete specimen's cross-section. Subsequently, an algorithm for the random convex polygon aggregate is proposed, in which an area of round aggregate is used as the control parameter and the inscribed polygon of the round aggregate is used as the framework. A numerical experiment is conducted on specimens under uniaxial compression by using the high-strength and high-performance concrete C80 as an example, and corresponding stress-strain curves and damage evolution pictures are drawn. A comparison between results of the numerical simulation and the physical test show that the numerical model proposed in this paper is both reasonable and feasible. high strength and high performance concrete; random aggregate model; mesoscale numerical simulation; damage evolution; damage finite element 2016-10-08 国家科技支撑计划(2013BAJ08B03);国家自然科学基金(51678475);教育部高等学校博士学科点专项科研基金(20136120110003) 郑 捷(1988-),女,陕西西安人,硕士,从事建筑与结构设计研究。E-mail:julie1314fl@126.com。 TU528.01 A 1000-0844(2016)05-0745-06 10.3969/j.issn.1000-0844.2016.05.0745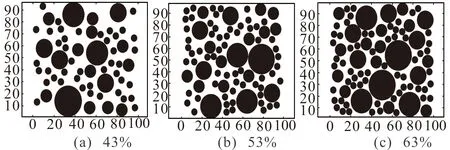
2 HSHPC随机骨料模型计算实例



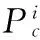




3 结语