岩质高陡边坡地震动响应规律的振动台试验研究

付 晓， 杨长卫， 韩宜康

(1.西南交通大学土木工程学院，四川 成都 610031； 2.南京铁道职业技术学院，江苏 南京 210031)



岩质高陡边坡地震动响应规律的振动台试验研究

付 晓1， 杨长卫1， 韩宜康2

(1.西南交通大学土木工程学院，四川 成都 610031； 2.南京铁道职业技术学院，江苏 南京 210031)

设计并完成了 1∶10大比例尺的边坡大型振动台模型试验，试验模型尺寸为 4.4 m×4.4 m×1.8 m(长×宽×高)，斜坡模型表面包含30°、45°、50°、60°四个不同坡度的坡面，模拟岩体材料采用重晶石粉、河砂、石膏、黏土和水按比例配制而成。通过输入不同类型、幅值、频率的地震波来研究模型边坡的动力响应规律，在试验数据分析中采用三维局部坐标系。试验结果表明：边坡临空面方向和竖直方向的加速度高程放大效应随坡面角度的增大而增强，在坡面角度由45°→50°变化时增长趋势呈明显“台阶状”形式，而边坡走向方向的峰值加速度高程放大效应基本不随坡面角度变化；边坡各向的峰值加速度的高程放大效应随着输入地震波幅值的增大而减小，表现出“量级饱和”特性；加速度傅里叶谱的频谱成分随着高程的增大，边坡岩体对于试验模型自振频率f周围的频率成分具有显著的放大作用，而对于其他频率成分则具有滤波作用；加速度反应谱沿高程的形状基本一致，并且卓越周期对应的反应谱幅值沿高程具有一定的放大作用，而在其他周期T处，尤其是长周期部分(低频部分)则存在一定的减小作用，对于临空面方向来讲，具有明显的波峰现象。试验结果有助于揭示边坡在地震作用下的失稳机制，为边坡工程的抗震设计提供有益的参考。

岩质边坡； 动力响应； 振动台试验； 地震动参数

0 引言

强震是引起边坡失稳破坏的重要因素。我国西部山区地震频发,引发了大量与地震有关的边坡稳定问题。地震作用下边坡的动力响应特性是揭示边坡地震失稳机制的前提，因此开展地震作用下边坡动力响应规律的研究是十分必要的。冯文凯等[1-3]对单面和双面斜坡在地震中的震裂变形破坏形成机制进行了探讨；毛彦龙等[4]认为地震动引起的坡体波动震荡是形成滑坡的主要因素；祁生文等[5]及李世海等[6]归纳了地震作用下边坡稳定性的影响因素，认为地震惯性力和超静孔隙水压力是导致边坡失稳的主要原因；崔芳鹏等[7-8]认为地震纵横波时差较短引起的耦合作用是斜坡体崩滑破坏的主控因素；张祖武等[9-10]对岩土界面地震波能量传递与耗散特性进行了研究；Chen H.J[11]通过离散元数值计算和试验两种手段研究了边坡的破坏特征；滕光亮等[12]借助数值计算探讨了地震作用下节理岩质边坡稳定性影响因素；韩宜康等[13]利用振动台试验及波动理论研究了坡面角度对岩质边坡加速度高程放大效应的影响。

为进一步认清地震诱发的斜坡崩滑机理及过程，本文借助大型振动台模型试验还原斜坡在地震时的动力响应，分析地震作用下坡体的动力响应规律以及改变输入地震波参数对其的影响。

1 振动台模型试验设计

振动台试验是在中国核动力研究设计院抗震试验室的大型三轴向六自由度地震模拟振动台上开展的。该试验设备是目前国内承载能力最大、性能最先进的地震模拟台，其台面尺寸为6 m×6 m，台面最大荷载质量为60 t，工作频率范围为0.1～80 Hz。试验采用刚性模型箱，内空尺寸为长、宽各5 m，高2.1 m(图1)。

图1 振动台试验模型箱Fig.11 Model box used in shaking table test

1.1 相似关系设计

在进行相似试验设计时，要使模型试验满足所有相似条件往往是很困难，甚至是不可能的。为使模型试验能够尽可能真实地反映原型的动力特性，应抓住影响现象内在规律的主要因素而省略一些次要准则。本次试验以模型尺寸L、重度γ和重力加速度g作为基本控制量，按Buckingham π定理和量纲分析法导出各物理量的相似关系和相似比(表1)。

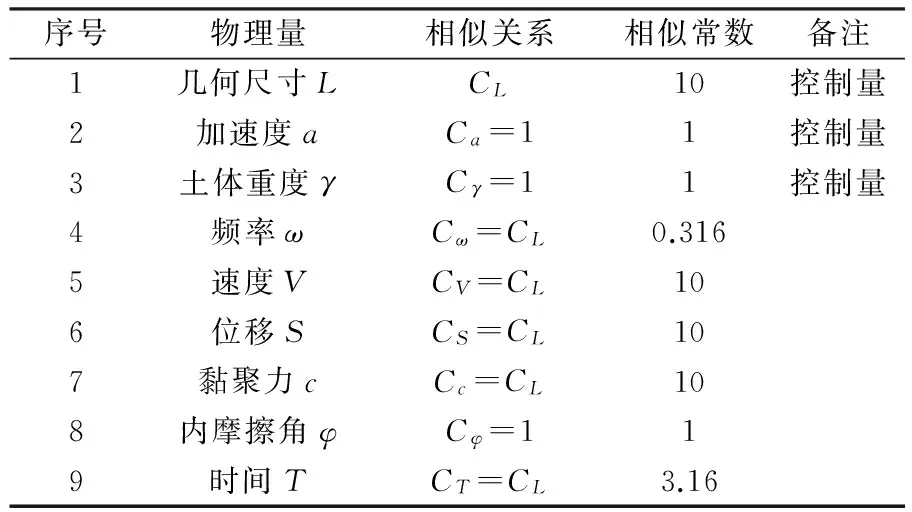
表 1 模型相似常数

1.2 相似材料配制

震害调查发现汶川震区岩质斜坡地层岩性主要分为两类：第一类是以薄层的千枚岩、绢云母片岩和厚层块状灰岩、砂岩为主的硬岩；第二类是以泥岩为典型代表的软岩。因此，本次模型试验基于上述的相似体系，选取软岩和硬岩作为岩质边坡的组成材料，参考前人总结的相似材料配比，采用重晶石粉、河砂、石膏、黏土和水作为原材料，通过调整各组分的质量比例来模拟不同岩体，其中软岩质量配比为河砂∶石膏∶水∶黏土=60.5∶16.1∶7.3∶16.1；硬岩质量配比为河砂∶石膏∶水∶黏土∶重晶石粉= 31.4∶15.7∶8.8∶18.9∶25.2。相似材料的具体物理力学指标见表2，室内配土试验见图2和图3。

图2 应变控制式直接剪切仪Fig.2 Strain-controlled direct shear apparatus

图3 环刀法测试土体重度Fig.3 Soil gravity test by cutting ring method

1.3 模型设计

针对汶川震区普遍发育的两大类岩体：硬岩类和软岩类，本试验采用不同岩性(包括以灰岩为代表的硬岩体)来模拟基岩，以泥岩、千枚岩为代表的软岩体来模拟坡体。另外，为了简化试验影响因素，试验模型采用均质结构，模型特征详见图4。斜坡模型的几何尺寸为：(1)总高1.8 m，其中边坡高0.8 m，下覆软岩和硬岩厚度均为0.5 m；长4.4 m，宽4.4 m；(2)斜坡模型的底部长3.53 m，宽1.55 m；上顶面长0.78 m，宽0.1 m；(3)斜坡模型表面包含30°、45°、50°和60°四个不同坡度的坡面。

表 2 试验材料中硬岩、软岩的物理力学参数

为减小地震波在模型箱边界的反射，最大程度地消除“边界效应”对试验结果的影响，试验时在激振方向模型箱侧壁上粘贴厚度为3 cm的泡沫吸波材料。

图4 振动台试验模型Fig.4 Test model

1.4 测点布置

为了研究斜坡的地震动力响应特性，试验时在四个坡面的不同高程处分别布置加速度传感器，同时，为了更加精确地描述地震过程中整个模型表面位移场的变化过程，本次试验采用自主研发的高频数字摄像系统对其进行监测，具体如下：

(1) 单向加速度传感器的布置

本次试验采用单向加速度传感器设置了两个自由场测点，主要监测地震作用下自由场内的加速度响应。其中，自由场1自上而下布置了3组加速度测点，自由场2则仅在场地表面布设了1组加速度测点(图5)。

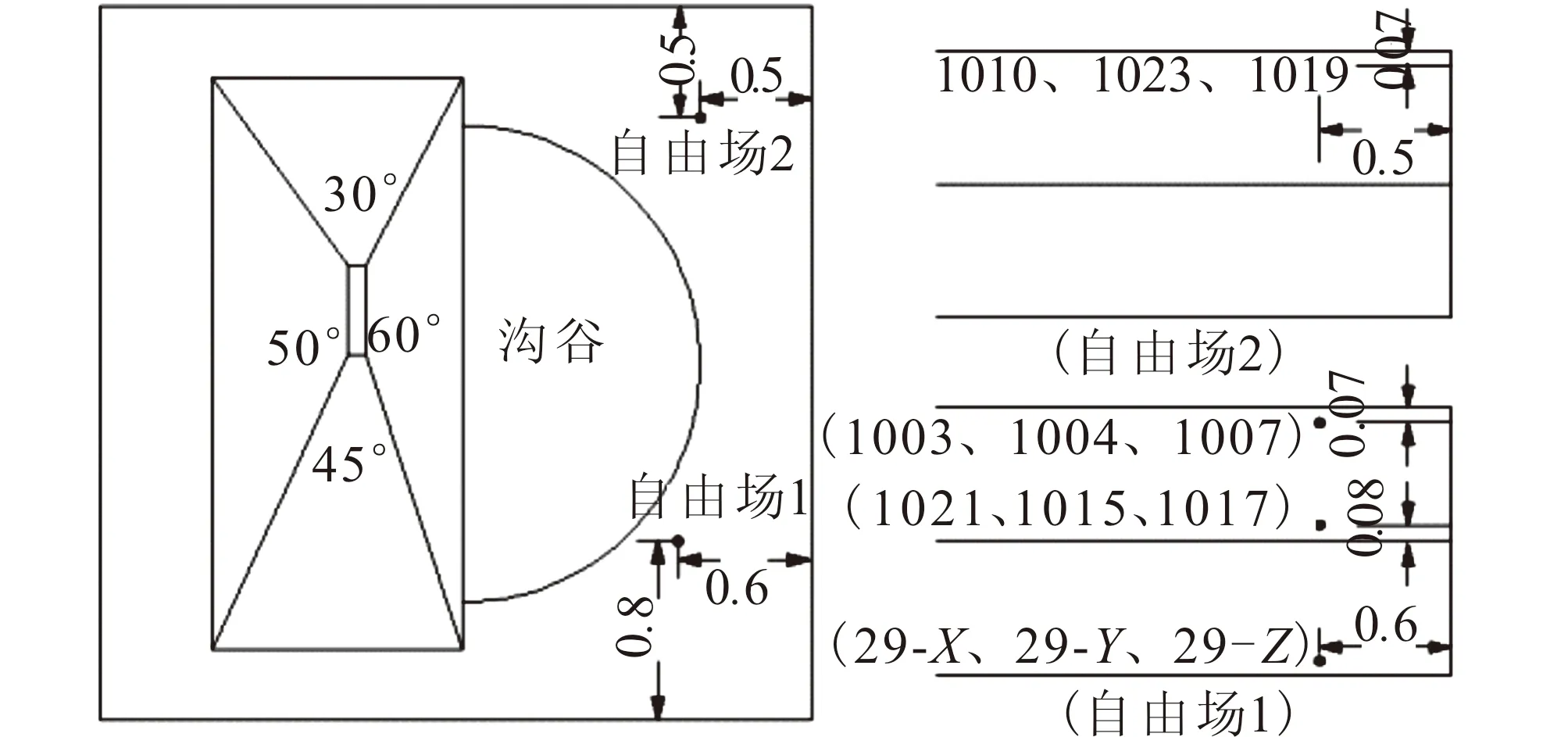
图5 自由场测点布置断面图Fig.5 Layout of observation spots on the free-field site

(2) 三向加速度传感器的布置

鉴于单向加速度器尺寸较大，而边坡体厚度相对较小，为避免因加速度测量元件的尺寸影响试验结果的精确性，在边坡体内均布置三向加速度传感器用于监测地震作用下坡体的动力响应规律，具体见图6。

(3) 高频数字化摄像系统的监测点布置

高频数字化摄像系统主要是用于研究地震过程中坡体的变形情况以及整个模型表面位移场的分布。本次振动台试验设置的监测点满布整个模型表面，呈0.2 m×0.2 m的网状分布(图4)。

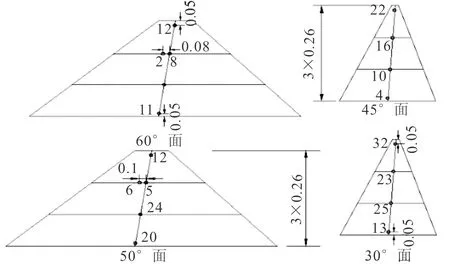
图6 坡面加速度传感器布置图Fig.6 Acceleration sensor layout on the slope surface

1.5 加载制度

根据相似原理，模型与原型输入地震加速度时程的波形是完全相同的，仅按照时间相似比进行了调整。本次试验旨在研究地震波类型、频率以及振幅对岩质边坡动力响应规律的影响，故首先对输入地震波进行归一化处理，之后通过调节其幅值来施加不同烈度的汶川卧龙地震波、El Centro地震波以及Kobe地震波的三向地震动加速度时程。具体加载制度如表3所示。

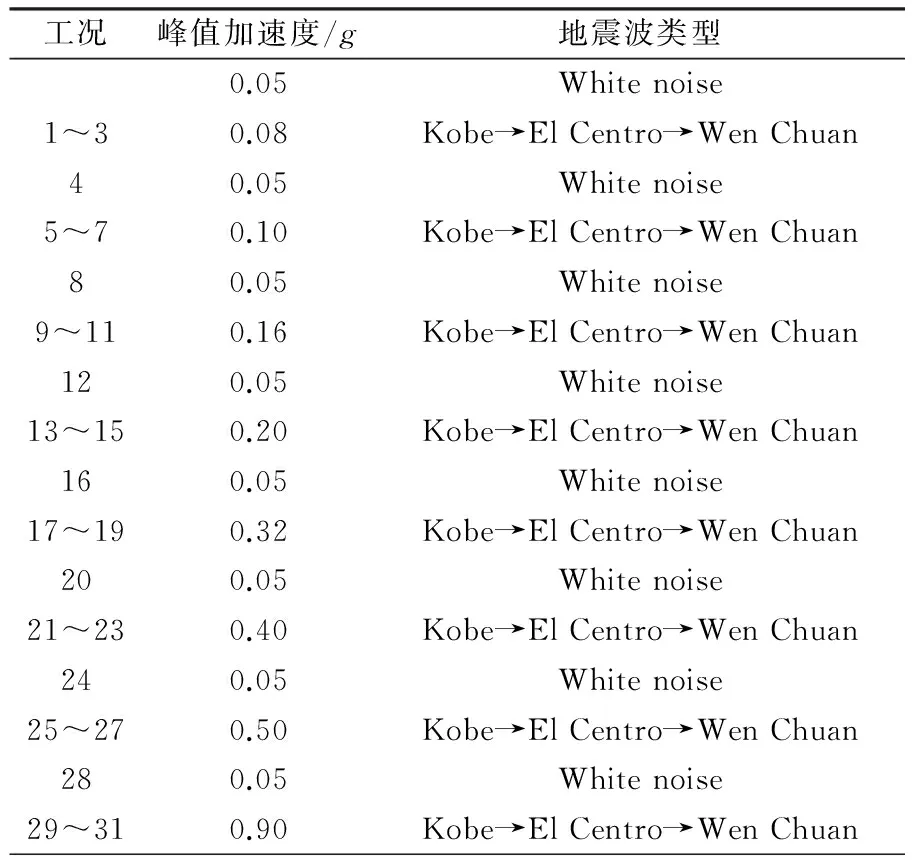
表 3 振动台试验的加载工况

2 模型边坡的动力响应

在边坡和支挡结构抗震设计时，目前广泛采用的拟静力方法是以加速度及其分布规律为基础的，用以计算地震引起边坡永久变形的Newmark滑块理论也以加速度反应为基础。因此，边坡的加速度响应特性是当前评价边坡地震稳定性和进行抗震设计的主要指标，并且在振动台模型试验时加速度的量测精度较高，因此本文选择对边坡体的加速度动力响应进行探讨。

2.1 加速度响应规律研究思路调整

如按常规的三维坐标系对模型试验中的边坡体进行分析，则会造成任意选定坡面的临空面方向是其余坡面的走向方向。基于此，本节以工况7的计算结果为例，选取两种坐标系对加速度的高程放大效应进行研究。第一种是现在使用最为广泛的X、Y、Z三向坐标系；第二种是局部坐标系，定义为边坡的走向M、边坡的临空面L、竖直方向N。整体坐标系和局部坐标系的具体情况见图7，第一种坐标系下试验分析结果见图8，后者的试验分析结果见图9。

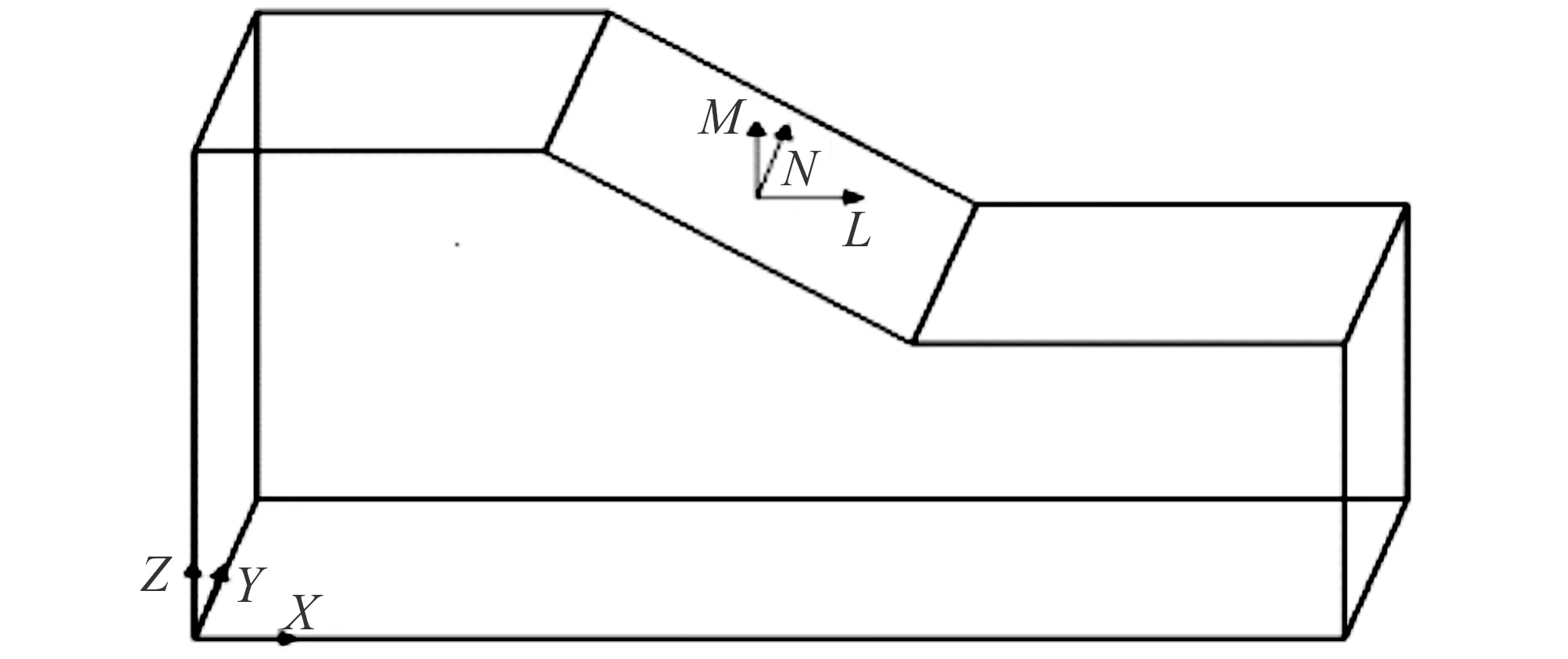
图7 坐标系变换示意图Fig.7 Diagram of coordinate system transformation

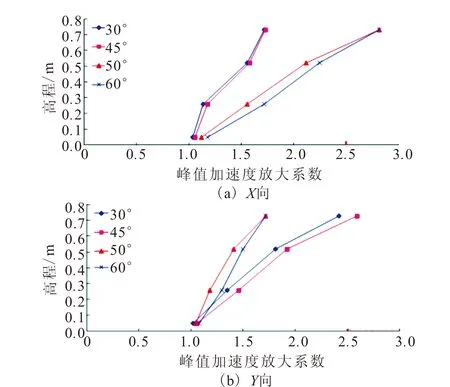
图8 整体坐标系下峰值加速度放大系数(0.1g)Fig.8 PGA amplification factors in the global coordinate system (0.1g)

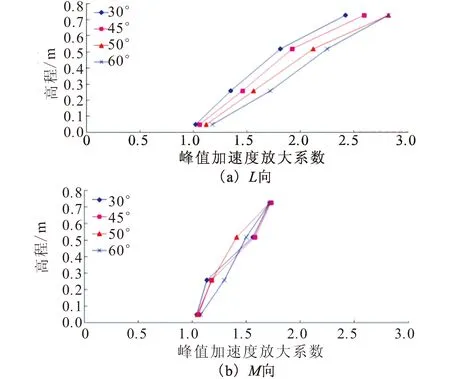
图9 局部坐标系下峰值加速度放大系数(0.1g)Fig.9 PGA amplification factors in the local coordinate system (0.1g)

综合分析图8、图9可知，在PGA=0.1g的汶川卧龙地震波作用下30°、45°、50°以及60°面上的X、Y方向峰值加速度沿高程均具有不同程度的放大。各坡面X方向的加速度放大性规律如下：60°面>50°面>45°面>30°面；Y方向的加速度放大性规律为:45°面>30°面>60°面>50°面。然而，在局部坐标系(L、M、N)下，各坡面L方向的加速度放大性规律与整体坐标系下X方向的加速度放大规律相同；而各坡面M方向的加速度放大性规律基本一致。由此可知，在整体坐标系下和局部坐标系下得到的结果是不一致的，出现上述现象可能是由于X(Y)方向对于50°、60°面来讲是临空面方向(边坡走向)，而此时30°面、45°面则是边坡的走向(临空面方向)。将边坡临空面的试验结果与边坡走向的试验结果进行对比来研究加速度的高程放大效应具有一定的片面性，很难清晰地研究坡面角度对坡面上加速度高程放大效应的影响。因此，本文将选取局部坐标系对加速度高程放大效应进行阐述。

2.2 模型边坡的加速度响应规律

为了研究加速度峰值的动力响应规律，将加速度放大系数定义为边坡内加速度峰值与自由场加速度峰值的比值。以L向加速度为例来说明：假定坡体内任意一点C的L向加速度峰值为ALC，自由场D点的X向加速度峰值为ALD，参见图10，则该点L向加速度放大系数δL就可以表示为：δL=ACL/ADL。

试验结果表明，在输入地震波类型和峰值加速度改变时，模型边坡加速度响应具有相似的规律。图11显示了60°坡面的三方向加速度峰值沿高程均具有不同程度的放大效应。

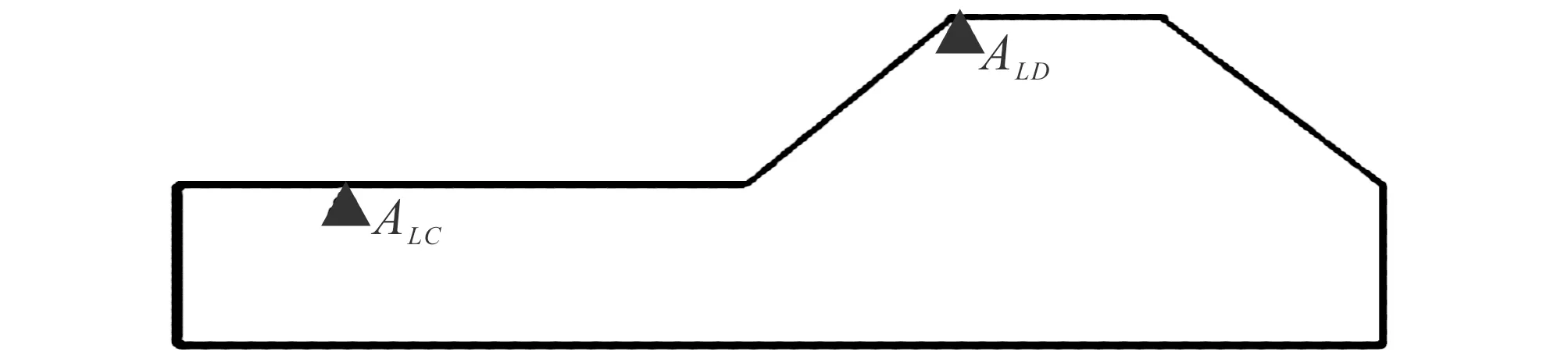
图10 模型示意图Fig.10 Schematic diagram of test model

图11 峰值加速度高程放大系数(60°坡面)Fig.11 PGA elevation amplification factors (slope angle =60°)

2.3 地震动参数对边坡的影响

坡面角度、地震烈度以及地震动输入波参数的差异对岩质边坡地震动特性均具有显著的影响。下文将研究在输入汶川卧龙地震波、El Centro地震波和Kobe地震波，且输入地震波峰值为0.08g、0.1g、0.16g、0.2g、0.32g、0.4g、0.5g和0.9g的情况下边坡体中不同坡面加速度高程的放大效应。

(1) 坡面角度的影响

目前大量研究成果表明坡面角度的不同对地震动加速度的放大效应具有显著影响。本节选取PGA=0.4g的汶川卧龙地震波激振结果，对坡体内各测点的三向加速度峰值放大系数进行分析，结果见图12。

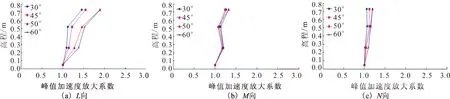
图12 PGA=0.4g时峰值加速度放大系数Fig.12 PGA amplification factors when PGA=0.4g

模型试验中边坡体各面各方向的峰值加速度沿高程均具有不同程度的放大。临空面和竖直方向的加速度放大系数均随着坡面角度的增加而增大；边坡走向的加速度放大系数基本不随角度的改变而变化。该试验结果也印证了岩质边坡问题可以近似地简化为平面应变问题。

本节选取距离边坡坡顶1/4H处的测点来揭示边坡角度对临空面、走向和竖直向加速度峰值放大效应的影响，具体结果见图13。加速度放大系数增长剧烈段发生在坡面角度由45°→50°时，加速度放大系数随坡面角度的增长而增加的趋势呈明显“台阶状”形式，台阶高度与坐标轴的关系为：临空面>竖直向>走向。上述分析结果充分说明了坡面角度为45°以上的岩质边坡的地震动响应明显高于坡面角度小于45°的岩质边坡，这与“5·12”汶川地震震害调查结果——滑坡灾害主要发生在40°以上的斜坡这一结论吻合。

(2) 地震烈度对加速度高程放大效应的影响

为了能够清晰地说明地震烈度对加速度高程放大效应的影响，本节仍选取距离边坡坡顶1/4H处的测点来揭示地震烈度对临空面、走向和竖直向加速度峰值放大效应的影响程度，具体计算结果见图14。

图13 边坡角度对加速度放大系数的影响(距坡顶1/4坡高处)Fig.13 Effect of slope angle on acceleration amplification factor (at 1/4H)

图14 地震烈度对加速度放大系数的影响(距坡顶1/4坡高处)Fig.14 Effect of seismic intensity on acceleration amplification factor at (1/4 H)

随着输入地震动峰值加速度的增加，边坡临空面、走向及竖直向的加速度高程放大效应逐渐减小，表现出“量级饱和”特性。量级饱和特性主要是指随着输入地震动峰值加速度的增大，岩土体的动剪切强度和动剪切模量下降，阻尼比增加，非线性特征逐渐增强，地震波的耗能增大，进而造成了加速度放大效应的减弱，岩土体的隔震、减震效果增强。

(3) 地震波类型对加速度高程放大效应的影响

本节选取边坡角度为60°坡面，PGA=0.2g的汶川卧龙地震波、El Centro地震波和Kobe地震波来说明地震动输入波类型对加速度高程放大效应的影响，具体结果见图15。边坡的临空面方向、走向方向和竖直方向的峰值加速度放大效应随输入地震波类型的变化规律基本一致，即El Centro波>汶川卧龙波>Kobe波。出现上述现象可能是由于这三种地震波压缩波的频谱特性存在较大差异造成的。

图15 地震波类型对峰值加速度放大系数的影响(PGA=0.2g，60°坡面)Fig.15 Effect of seismic wave type on PGA amplification factor (PGA=0.2g,slope angle=60°)

2.4 加速度傅里叶谱沿高程的变化规律

鉴于L、M、N三个方向的加速度傅里叶谱沿高程变化规律基本一致，限于篇幅，本节仅选取PGA=0.2g的汶川卧龙地震波作用下45°坡面上各个测点的临空面方向加速度时程进行分析。该坡面上布置的加速度测点见图6，计算结果见图16。

临空面方向加速度傅里叶谱的频谱成分沿高程的变化均具有一定的规律，即随着高程的增大，边坡岩体对于3.69～5.48 Hz频率成分的地震波具有显著放大作用，而对于其他频率成分的地震波则具有滤波作用。出现上述现象可能是由于该边坡试验模型的第一阶自振频率为4.5 Hz，进而引起了3.69～5.48 Hz频率成分的放大。这与通常所说的“边坡土体对地震波的高频成分具有滤波作用，对于低频成分具有放大作用”这一结论是一致的。

2.5 加速度反应谱沿高程的变化规律

地震作用下岩质边坡加速度反应谱的形状对认识边坡动力响应特征及边坡的治理设计具有重要的参考价值。为了研究岩质边坡加速度反应谱沿高程的变化规律，本节仍选取峰值加速度为0.2g的汶川卧龙地震波作用下45°坡面上各个测点的L、M、N三向加速度时程进行分析。为了能够更加清晰地说明反应谱中不同周期谱值的高程放大效应，本节以边坡底部的测点4的三向反应谱作为基准，求解10、16及22测点加速度反应谱的放大系数，具体计算结果见图17～18。本次加速度反应谱计算采用了工程上常用的阻尼比5%。

图16 临空面方向加速度傅里叶谱Fig.16 Acceleration Fourier spectrum along L direction

图17 45°坡面加速度反应谱Fig.17 Acceleration response spectrum along 45° slope surface

图18 45°坡面加速度反应谱放大系数Fig.18 Acceleration response spectrum amplification factor along 45° slope surface

边坡的临空面方向、走向方向及竖直方向的加速度反应谱存在一定的共性和差异性。共性为：三个方向的加速度反应谱沿高程的形状基本一致，卓越周期集中在T=0.22 s左右，即卓越频率f=4.54 Hz，并且卓越周期对应的反应谱幅值沿高程具有一定的放大作用，而在其他周期T处，尤其是长周期部分(低频部分)则存在一定的减小作用，这与傅里叶谱的计算结果基本一致。差异性：加速度反应谱的频率分布存在一定的差异，对于临空面方向来讲，具有明显的波峰现象；对于边坡走向和竖直方向来讲，波峰现象不如临空面方向明显。

3 结论

本文设计并完成一个1∶10 大比例尺的边坡大型振动台模型试验，研究地震作用下模型边坡的动力响应规律，得到以下结论：

(1) 对于包含不同坡面角度的山体来讲，按照常规方法使用X、Y、Z坐标系对加速度高程放大效应进行分析，具有一定的片面性，即X方向既是某一坡面的临空面方向又是另一个坡面的边坡走向方向，不能清晰地反映坡面角度的影响。因此建议采用三维局部坐标系，即边坡的临空面方向、走向方向和竖直方向来研究边坡的动力问题。

(2) 在坡面角度由45°→50°变化时，临空面方向和竖直方向加速度放大系数的增加趋势呈明显“台阶状”形式，而边坡走向方向的峰值加速度高程放大效应与角度基本无关。

(3) 边坡临空面、走向及竖直方向的峰值加速度的高程放大效应随着输入地震波幅值的增大而减小，表现出“量级饱和”特性；地震波类型对局部坐标系下加速度高程放大效应的影响是：El Centro地震波>汶川卧龙地震波>Kobe地震波。

(4) 边坡的临空面方向、走向方向及竖直方向的加速度傅里叶谱的频谱成分沿高程的变化均具有一定的规律性，即随着高程的增大，边坡岩体对于试验模型自振频率f周围的频率成分具有显著的放大作用，而对于其他频率成分则具有滤波作用。

(5) 边坡的临空面方向L、走向方向M及竖直方向N的加速度反应谱沿高程的形状基本一致，并且卓越周期对应的反应谱幅值沿高程具有一定的放大作用，而在其他周期T处，尤其是长周期部分(低频部分)则存在一定的减小作用。另外，对于临空面方向来讲具有明显的波峰现象；对于边坡走向和竖直方向来讲，波峰现象不如临空面方向明显。

References)

[1] 冯文凯,许强,黄润秋.斜坡震裂变形力学机制初探[J].岩石力学与工程学报,2009,28(1):3124-3130.

FENG Wen-kai,XU Qiang,HUANG Run-qiu.Preliminary Study on Mechanical Mechanism of Slope Earthquake Induced Deformation[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(1):3124-3130. (in Chinese)

[2] 张倬元,王士天,王兰生.工程地质分析原理[M].北京：地质出版社,1993.

ZHANG Zhuo-yuan,WANG Shi-tian,WANG Lan-sheng.Principles of Engineering Geology[M].Beijing:Geological Publishing House,1993.(in Chinese)

[3] 胡光韬.滑坡动力学[M].北京：地质出版社,1995.

HU Guang-tao.Dynamics of Landslides[M].Beijing:Geological Publishing House,1995.(in Chinese)

[4] 毛彦龙,胡广韬,毛新虎,等.地震滑坡启程剧动的机理研究及离散元模拟[J].工程地质学报,2001,9(1)：74-80.

MAO Yan-long,HU Guang-tao,MAO Xin-hu,et al.Mechanism of Set-out Violent-slide of Slope Mass During Earthquake and Its Simulation by Using Discrete Element Method[J].Journal of Engineering Geology,2001,9(1):74-80.(in Chinese) [5] 祁生文,伍法权,刘春玲,等.地震边坡稳定性的工程地质分析[J].岩石力学与工程学报,2004,23(16)：2792-2797.

QI Sheng-wen,WU Fa-quan,LIU Chun-ling,et al.Engineering Geology Analysis of Stability of Slope under Earthquake[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(16):2792-2797.(in Chinese)

[6] 李世海,刘天萍,刘晓宇.论滑坡稳定性分析方法[J].岩石力学与工程学报,2009,28(增刊2):3309-3324.

LI Shi-hai,LIU Tian-ping,LIU Xiao-yu.Analysis Method for Landslide Stability[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(Sup.2):3309-3324.(in Chinese)

[7] 崔芳鹏,胡瑞林,殷跃平,等.地震纵横波时差耦合作用的斜坡崩滑效应研究[J].工程地质学报,2009,17(4):455-462.

CUI Fang-peng,HU Rui-lin,YIN Yue-ping,et al.Numerical Simulation of Slope Collapsing and Sliding due to Single of Combined Actions of Seismic P and S Waves with Time Difference[J].Journal of Engineering Geology,2009,17(4):455-462.(in Chinese)

[8] 崔芳鹏,胡瑞林,殷跃平,等.纵横波时差耦合作用的斜坡崩滑效应离散元分析——以北川唐家山滑坡为例[J].岩石力学与工程学报,2010,29 (2):319-327.

CUI Fang-peng,HU Rui-lin,YIN Yue-ping,et al.Discrete Element Analysis of Collapsing and Sliding Response of Slope Triggered by Time Difference Coupling Effects of P and S Seismic Waves——Taking Tanjiashan Landslide in Beichuan County for Example[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(2):319-327.(in Chinese)[9] 张义平,李夕兵,赵国彦,等.爆破震动信号的时频分析[J].岩土工程学报,2005,27(12):1472-1476.

ZHANG Yi-ping,LI Xi-bing,ZHAO Guo-yan,et al.Time-frequency Analysis of Blasting Vibration Signals[J].Chinese Journal of Geotechnical Engineering,2005,27(12):1472-1476.(in Chinese)

[10] 张祖武,姚令侃.土岩界面地震波能量传递与耗散特性研究——以汶川8.0级地震为例[J].灾害学,2011,26(1):4-9.

ZHANG Zu-wu,YAO Ling-kan.Seismic Waves Scattering in Rock Interface and Energy Dissipation Characteristics——TakingM8.0 Wenchuan Earthquake as an Example[J].Journal of Catastrophology,2011, 26(1):4-9. (in Chinese)

[11] Chen H J,Liu S H.Slope Failure Characteristics and Stabilization Methods[J].Canadian Geotechnical Journal,2007,44(4)：377-391.

[12] 滕光亮,陈永明,石玉成,等.地震作用下节理岩质边坡稳定性影响因素研究[J].地震工程学报, 2013,35(1):119-125.

TENG Guang-liang,CHEN Yong-ming,SHI Yu-cheng,et al.A Study on the Influencing Factors of Joint Rock Slope Stability under Earthquake Activity[J].China Earthquake Engineering Journal,2013,35(1):119-125. (in Chinese)

[13] 韩宜康,杨长卫,张建经,等.坡面角度对岩质边坡加速度高程放大效应的影响[J].地震工程学报,2014,36(4):874-880.

HAN Yi-kang,YANG Chang-wei,ZHANG Jian-jing,et al.The Influence of Slope Angle on the Elevation Amplification Effect of Rock Slope Acceleration[J].China Earthquake Engineering Journal,2014,36(4): 874-880.(in Chinese)

Shaking Table Model Tests on the Seismic Response of a High and Steep Rock Slope

FU Xiao1, YANG Chang-wei1, HAN Yi-kang2

(1.SchoolofCivilEngineering,SouthwestJiaotongUniversity,Chengdu610031,Sichuan,China; 2.NanjingInstituteofRailwayTechnology,Nanjing210031,Jiangsu,China)

A large-scale shaking table model test of a slope with a height of 1.8 m, length of 4.4 m, and width of 4.4 m was introduced. The materials are made of blanc fixe, river sand, gypsum, clay, and water in different ratios. The slope comprises 30°, 45°, 50°, and 60° inclined surfaces. A series of tests were performed for different seismic waves, amplitudes, and frequencies. The results indicate that the local coordinate system is more adequate than the whole coordinate system when conducting research on the dynamic problems of the slope. Thus, we should use the airport surface directionL, the strike directionM, and the vertical directionN. The amplifications of the peak accelerations gradually increase with the increase of slope angles, and there are two inflection points at 45° and 50°. However, the amplification along the slope strike direction is consistent. The amplifications of the accelerations in different directions gradually reduce with the increase of the peak ground acceleration of the input wave, which is an intensity saturation phenomenon. Simultaneously, there are predominant peak values in the airport surface directionL; however, there are no predominant peak values in the strike directionMand in the vertical directionN. Therefore, the results reveal the mechanism of slope instability during an earthquake and provide seismic design references for slope engineering.

rock slope; dynamic response; shaking table test; ground motion parameter

2015-11-04

交通运输部建设科技项目(2013318800020)

付 晓(1987-)，男，博士研究生，主要从事边坡与支挡结构抗震等方面的研究。E-mail:f_u_xiao@126.com。

TU457

A

1000-0844(2016)05-0775-08

10.3969/j.issn.1000-0844.2016.05.0775