直接基于位移设计的高强钢组合K形偏心支撑钢框架的抗震性能研究

郑晓伟, 苏明周, 石 鲁, 秦 瑞, 王迪涛, 王 喆

(1.大连理工大学建设工程学部，辽宁 大连 116000; 2.西安建筑科技大学土木工程学院，陕西 西安 710055;3.中国建筑标准设计研究院有限公司,北京 10048)



直接基于位移设计的高强钢组合K形偏心支撑钢框架的抗震性能研究

郑晓伟1,2, 苏明周2, 石 鲁2, 秦 瑞2, 王迪涛2, 王 喆3

(1.大连理工大学建设工程学部，辽宁 大连 116000; 2.西安建筑科技大学土木工程学院，陕西 西安 710055;3.中国建筑标准设计研究院有限公司,北京 10048)

K形高强钢组合偏心支撑(K-HSS-EBF)是指耗能连梁和支撑采用Q345钢，而框架梁、框架柱采用高强度钢(如Q460)。为研究其在罕遇地震作用下的抗震性能，在试验研究的基础上，采用直接基于位移的抗震设计方法设计了5层、8层和12层算例，分别进行静力推覆分析和动力弹塑性分析，研究高强钢组合偏心支撑钢框架在罕遇地震作用下层间侧移分布和破坏模式。研究结果表明：直接基于位移的抗震设计方法设计的算例在罕遇地震作用下，结构的层间侧移满足我国现行抗震规范的要求，结构呈理想的渐进式梁铰屈服机构，并证明该设计方法的合理性和可靠性。

偏心支撑钢框架； 高强钢； 直接基于位移的抗震设计； 层间位移; 破坏模式

0 引言

偏心支撑钢框架兼有中心支撑钢框架的抗侧刚度和抗弯钢框架的良好延性。其作用机理是在地震作用下通过耗能连梁的非弹性变形消耗地震能量，保证其他构件不屈曲或屈曲在后[1-3]。偏心支撑结构是采取放大内力方法进行传统设计，这势必造成非耗能构件(如框架梁、框架柱)的截面过大[4-5]，而高强钢组合偏心支撑很好地解决了这个问题，它是指耗能连梁采用普通钢材(如Q345)，框架梁和框架柱等非耗能构件采用高强度钢材(如Q460)，从而减小构件截面，节省钢材，获得可观的经济效益。

本课题组对多层高强钢组合K形偏心支撑进行了振动台试验研究。研究表明，多层高强钢组合K形偏心支撑在地震作用下具有良好的抗震性能。本文采用直接基于位移(DDBD)的抗震设计方法设计三组算例，并利用 SAP2000 非线性有限元软件对算例进行静力推覆分析和动力弹塑性分析，评估结构的抗震性能，进而验证DDBD设计方法的合理性和可靠性。

1 试验概况与有限元验证

1.1 试验试件及加载工况

试验为三层单跨两榀的1:2缩尺K-HSS-EBF空间模型试件振动台试验。试件跨度2.825 m，层高1.8 m，C30楼板厚80 mm(图1)。耗能梁段、支撑采用Q345B钢，框架梁、柱采用Q460C钢，钢材力学性能参数如表1所列。耗能梁段长350 mm，均为剪切屈服型(eVp/Mp=1.06，Vp和Mp分别为耗能梁段的塑性抗剪承载力和塑性受弯承载力)，各构件之间均采用焊接连接，构件截面尺寸如表2所列。

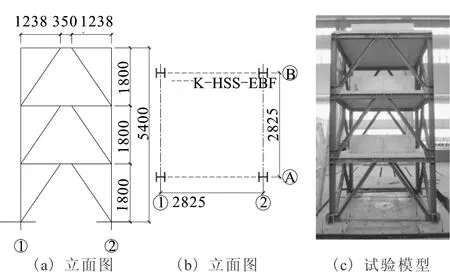
图1 模型尺寸(单位：mm)Fig.1 Dimension of the experimental specimen (Unit:mm)

表 1 钢材性能参数

表 2 构件截面尺寸

试件模型各层楼面及屋面均布置加速度传感器及位移传感器，试验为单向加载，地震波输入按照加速度从小到大的顺序进行，各工况台面输入加速度相似比为1.2∶1。试验工况如表3所列。

表 3 试验加载工况

1.2 有限元模型及分析结果对比

为验证所用有限元分析模型的正确性，采用结构分析软件SAP2000建立振动台试验试件的有限元模型(图2)，并对结构进行试验工况分析。表4和表5仅给出了试验试件在Ⅷ度多遇和罕遇地震水准El-Centro波作用下的加速度和位移有限元计算值与实测值的比较。研究结果表明，有限元计算结果与试验结果较为接近，因此可利用有限元软件SAP2000来进行本文所有模型的分析。

表 4 有限元计算最大加速度与试验结果比较

表 5 有限元计算最大相对位移与试验结果比较

图2 试验试件有限元模型Fig.2 The finite element model of test specimen

2 分析模型

2.1 直接基于位移的抗震设计方法

本课题组针对偏心支撑结构体系提出了直接基于位移的抗震设计方法(direct displacement-based design，以下简称DDBD)。此方法的核心理念是用单自由度体系代替多自由度体系，并通过单自由度体系的结构特征来研究多自由度体系。采用DDBD方法设计偏心支撑结构的设计过程为：

(1) 确定算例结构的性态水准，主要研究高强钢组合偏心支撑结构在罕遇地震作用下的性能研究；

(2) 确定算例结构等效单自由度体系的等效质量和等效高度，根据文献[6]中提供的方法得到He；

(3) 根据文献[6]中提供的方法计算得到各算例的目标位移为Δd;

(4) 确定算例结构的等效阻尼比。国内外对等效阻尼比的研究很多，Blandon[7]在前人研究的基础上,根据等能量耗散准则，提出了适合于不同恢复力模型的等效阻尼比估算公式。结合偏心支撑结构的恢复力特性确定其等效单自由度体系的等效阻尼比ζe。

(5) 确定结构的等效周期。根据文献[6]中提供的方法计算得到Te。

2.2 算例概况

高强钢组合偏心支撑算例中，耗能连梁和支撑为Q345钢，框架梁和框架柱为Q460钢；普通钢偏心支撑算例构件材料均为Q345钢，材料屈服强度均取名义值，弹性模量取2.06×105 MPa。算例设计共三组，分别为5层、8层以及12层。

三组算例均位于Ⅷ度(0.3g)抗震设防区，设计地震分组为第一组，场地类别为Ⅱ类，平面尺寸21.6 m×36.0 m，柱距7.2 m，层高3.6 m，耗能梁段长度900 mm，采用120 mm厚现浇混凝土楼板，C30混凝土。框架柱采用箱形截面，其他构件截面均采用焊接H型钢，翼缘为焰切边。楼面恒载取5.0 kN/m2(包括楼板自重)，活载取2.0 kN/m2，屋面恒载取6.0 kN/m2，上人屋面活荷载取2.0 kN/m2，雪荷载0.35 kN/m2，基本风压0.35 kN/m2。算例平面布置如图3所示，由2.1节得到的设计参数列于表6。

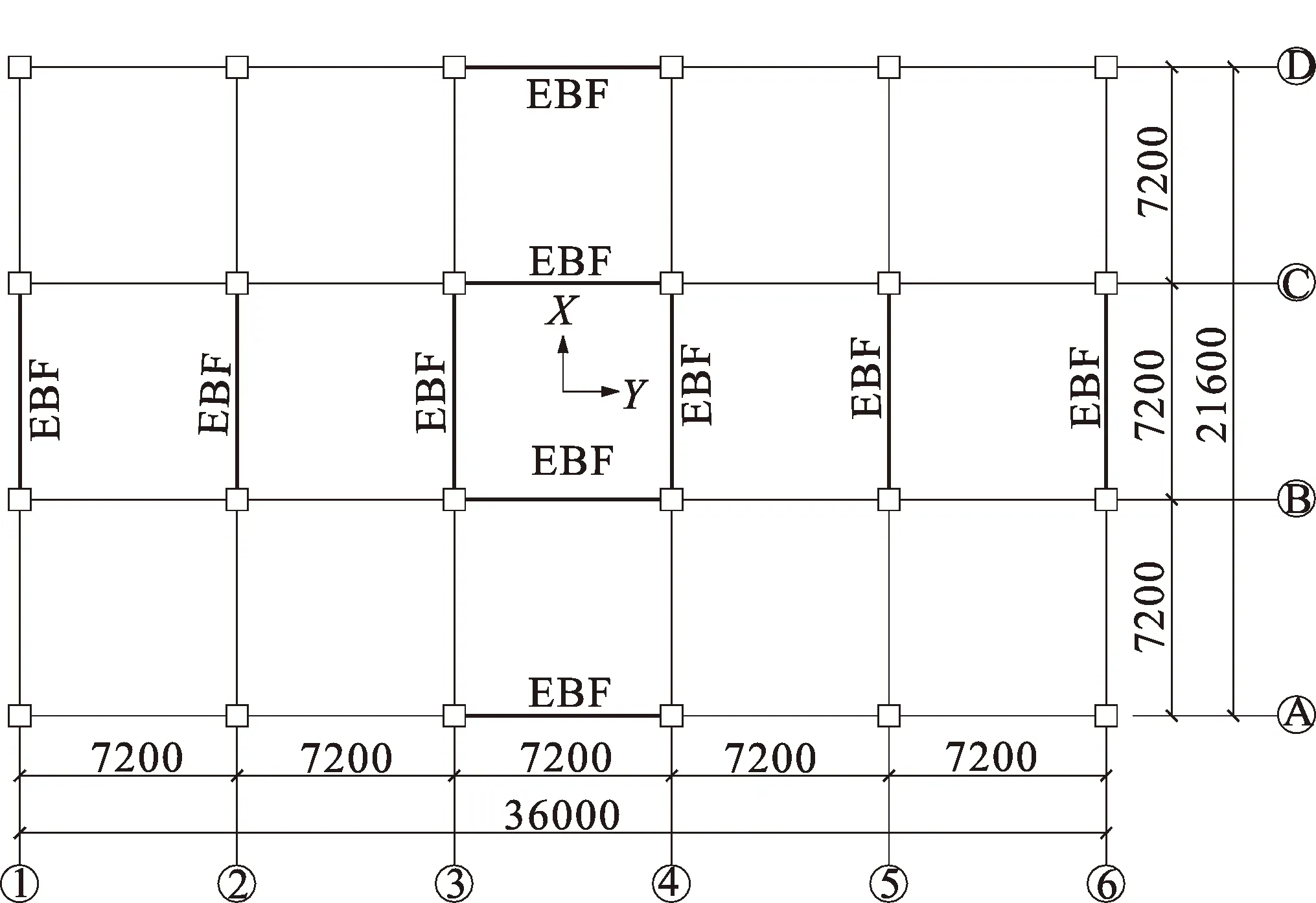
图3 算例平面布置图(单位：mm)Fig.3 Plan view of the example (Unit:mm)

表 6 三组算例的设计参数

2.3 算例截面

通过直接基于位移设计得到的三组K形偏心支撑钢框架的截面尺寸列于表7～表9。

3 静力推覆分析

3.1 能力曲线

采用Pushover分析方法对三组算例进行抗震性能评估，其中水平荷载采用倒三角分布模式，得到结构基底剪力与框架顶点侧移的能力曲线(图4)。限于篇幅，本文仅列出5层算例荷载位移曲线及其转化成能力谱曲线的过程。为确定其能够代表结构抗震性能的目标位移，需要将图4中的荷载位移曲线转化成能力谱曲线，以此求解算例结构的性能点。

表 7 5层构件截面(单位：mm)

表 8 8层构件截面(单位：mm)

表 9 12层构件截面(单位：mm)

(1) 利用式(1)、式(2)分别计算出结构顶层的一阶振型参与系数γ1=20.5和第一振型的有效质量M1=4.5×106kg；

(1)

(2)

式中:mi为楼层的质量；φi1为基本振型在i楼层的振幅值；n为楼层数；M1为基本振型下的有效质量；γ1为基本振型的参与系数。

(2) 由式(3)、式(4)将图4中的荷载位移曲线转化为能力谱曲线；

(3)

(4)

式中:V为结构的基底剪力；Δ为结构的顶点位移；φn1为基本振型在顶层的振幅值。

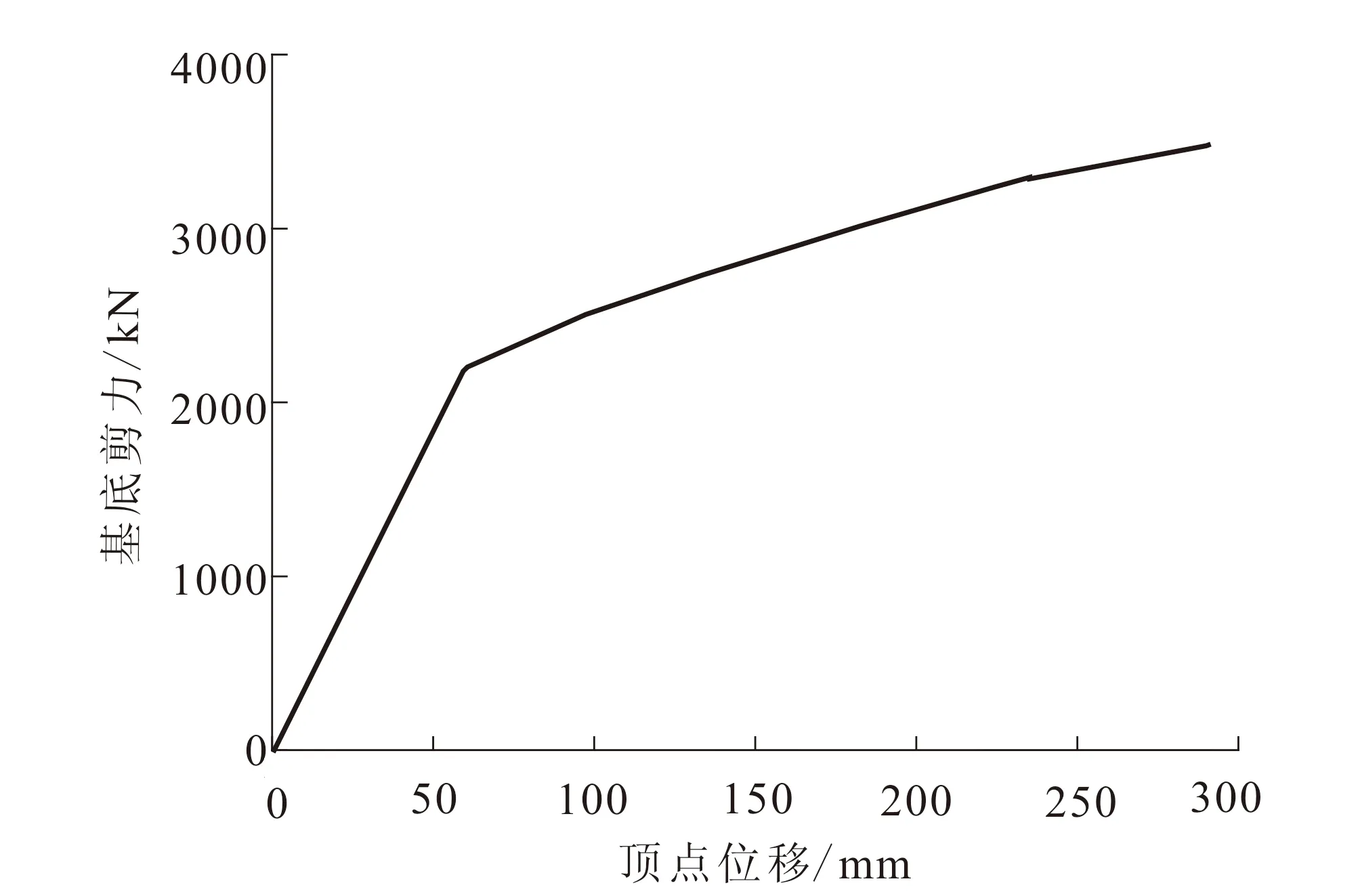
图4 5层算例的能力曲线Fig.4 Capacity curve of 5-story model

(3) 由式(5)将《建筑抗震设计规范》GB50011-2010[8](以下简称《抗规》)中的标准反应谱曲线分别转化为弹性(ζe=ζ0=0.05)需求谱和弹塑性(ζe=ξ0+ξh)需求谱曲线；

(5)

式中:α为地震影响系数；g为重力加速度，取g=9.8 m/s2。

(4) 将上述得到的能力谱曲线和需求谱曲线在同一坐标系中绘出，两条曲线的交点即为所求的性能目标Δ5=121.4 mm (Δ8=160.0 mm、Δ12=270.8 mm)，如图5所示。其中，Δ5表示5层算例性能点处结构顶点的位移，以此类推。

(5) 将上述得到的性能目标代回算例的能力曲线中，根据Push-over各步的计算结果，进一步得到结构此时的层间侧移角(表10)。

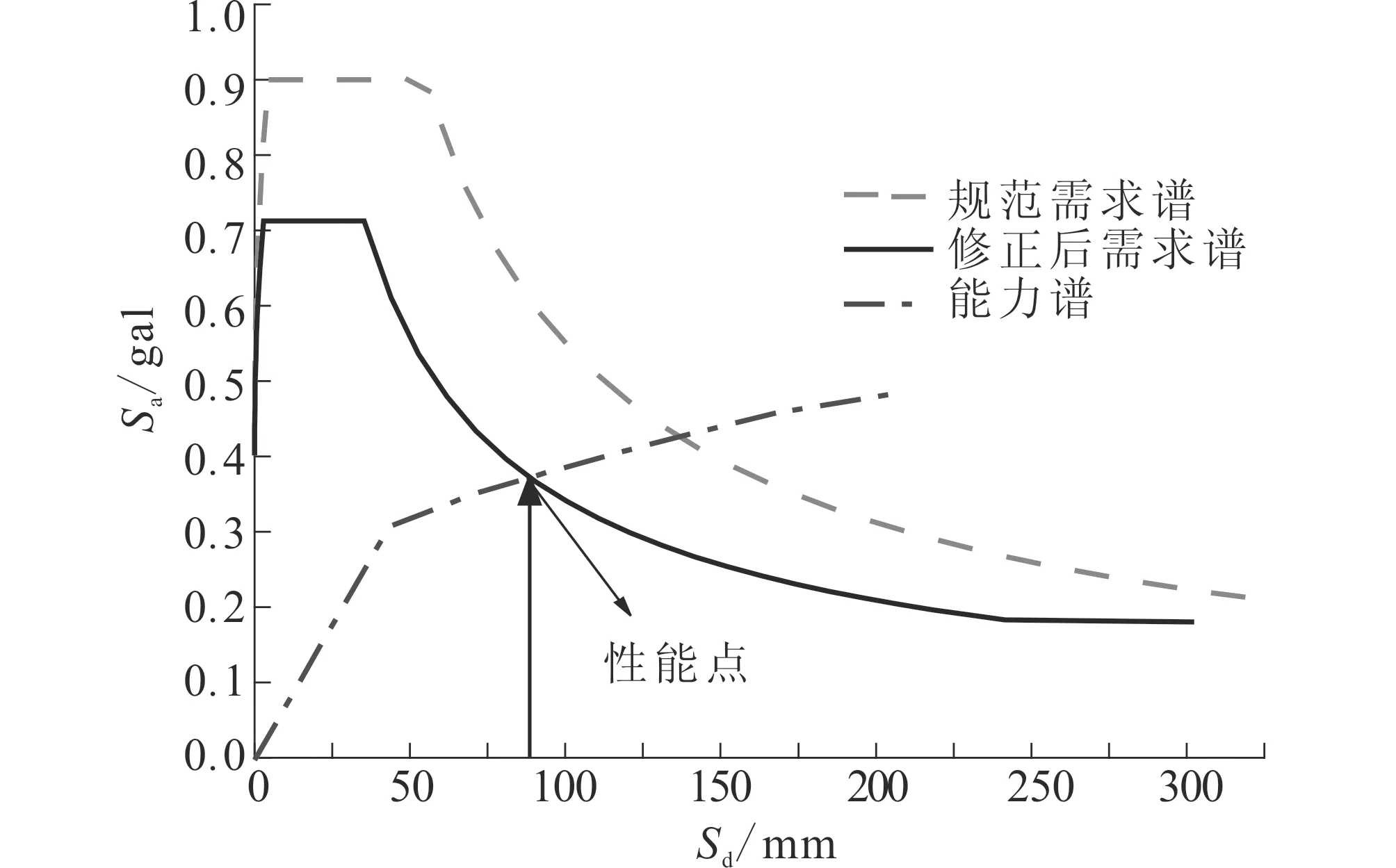
图5 性能点的确定Fig.5 Determination of the performance point

表 10 各算例的层间侧移角

如表10所列，结构达到性能点时，层间侧移角均远小于《抗规》中的弹塑性层间侧移角限值2%，说明结构有足够的安全储备以保证不倒塌。

3.2 塑性铰分布

图6给出了三组偏心支撑结构达到极限变形状态时的塑性铰分布。由图可知，经DDBD方法设计的算例模型的破坏模式：在耗能连梁上均出现塑性铰，框架梁作为抗震设防的二道防线两端受弯屈服，偏心支撑结构呈现出理想的破坏模式。

4 时程分析

偏心支撑结构体系依据DDBD方法设计，主要是在罕遇地震作用下进行耗能连梁截面的确定，故三组算例进行设计条件下的罕遇地震水准的时程分析，结果更具可靠性。

4.1 地震波选取

三组算例具有相同的场地条件和特征周期，根据《抗规》，地震波要符合三要素：频谱特性、有效峰值和持续时间。地震波选取依据算例地震分组与场地类别条件，从太平洋地震工程研究中心(http://peer.berkeley.edu/smcat/)严格筛选8条天然地震波,每条地震波的频谱特性各不相同。天然波属性列于表11。

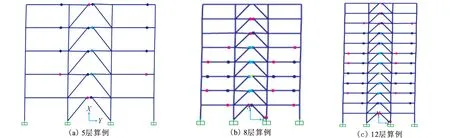
图6 算例破坏模式Fig.6 Failure modes of the examples

表 11 地震记录

4.2 典型的失效模式

限于文章篇幅，本文仅列出El Centro波作用下结构的塑性铰分布状态(图7)。

由图7可知，偏心支撑结构体系在地震波作用下耗能连梁发挥了主要的耗能作用，结构受力状态基本为耗能梁段进入塑性，而其余构件大都处于弹性状态，表明结构在罕遇地震作用下具有足够的安全储备，符合多道抗震设防的原则。

图7 算例破坏模式Fig.7 Failure modes of the examples

4.3 层间侧移

各算例的层间侧移包络图如图8所示。结构在罕遇地震作用下，层间侧移角沿结构高度方向分布较均匀，说明结构的弹塑性变形沿高度方向趋于均匀，使得各层耗能梁段均能参与耗能，符合DDBD的设计理念；结构各层侧移角分布在0.18%～0.78%间，均小于抗震规范规定的弹塑性层间侧移角限值H/50(2%)。

图8 算例的层间侧移角Fig.8 Interstory drift angles of each example

5 结论

本文在多层高强钢组合K形偏心支撑振动台试验研究的基础上，依据直接基于位移的抗震设计方法设计了三组高强钢组合偏心支撑，并分别进行了结构的静力推覆分析和动力弹塑性分析，得出结论如下：

(1) 直接基于位移的性态设计方法设计的高强钢组合K形偏心支撑钢框架破坏模式为耗能连梁呈剪切屈服，边框梁受弯屈服及柱根部进入塑性作为性能极限状态。满足性能目标和设计原则：耗能连梁作为主要的耗能构件进入塑性耗能，而其他构件保持弹性。因此，高强度钢材可以在抗震设防区的建筑中应用推广。

(2) 本文算例结构具有较强的水平抗侧能力，且满足罕遇地震水准下结构变形的规范要求，最终呈现理想的梁铰破坏机构，从而验证了DDBD性态设计方法的合理性和可靠性。同时该设计方法具有概念清晰、操作简单等优点。

References)

[1] 石永久, 熊俊, 王元清,等.多层钢框架偏心支撑的抗震性能试验研究[J].建筑结构学报,2010,31(2): 29-34.

SHI Yong-jiu,XIONG Jun,WANG Yuan-qing,et al.Experimental Studies on Seismic Performance of Multi-storey Steel Frame with Eccentric Brace[J].Journal of Building Structures,2010,31(2):29-34.(in Chinese)

[2] Malley J O,Popov E P.Shear Link in Eccentrically Braced Frames[J].Journal of Structural Engineering,1984,110(9):2275-2295.

[3] Dubina D,Stratan A,Dinu F.Dual High-strength Steel Eccentrically Braced Frames with Removable Links[J].Earthquake Engineering and Structural Dynamics,2008,37(15):1703-1720.

[4] Bosco M,Marino E M,Rossi P P.Proposal of Modifications to the Design Provisions of Eurocode 8 for Buildings with Split K Eccentric Braces[J].Engineering Structures,2014,61(1):209-223.

[5] 蔡益燕,钱稼茹,郁银泉.偏心支撑框架设计新进展[J].建筑结构,2011,41(4):7-10.

CAI Yi-yan,QIAN Jia-ru,YU Yin-quan.Advance in Eccentrically Braced Frame Design[J].Building Structure,2011,41(4):7-10.(in Chinese)

[6] 苏明周，郑晓伟.K形偏心支撑钢框架直接基于位移的抗震设计方法研究[J].地震工程学报，(已录用).

SU Ming-zhou,ZHENG Xiao-wei. Direct displacement-based Design Method of K-eccentrically Braced Frames[J].China Earthquake Engineering Journal.(in Chinese)

[7] Balandon CA,Priestley M J N.Eqquivalent Viscous Damping Equations for Direct Displacement-ased Design[J].Journal of Earthquake Engineering，2005，9:257-278.

[8] GB50011-2010,建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.

GB50011-2010,Code for Seismic Design of Buildings[S].Beijing:China Architecture & Building Press,2010. (in Chinese)

[9] 卢育霞,石玉成,万秀红,等.近地表速度结构对场地强地震动特征的影响[J].地震工程学报,2014,36(4):813-819.

LU Yu-xia,SHI Yu-cheng,WAN Xiu-hong,et al.Influence of Near-surface Velocity Structure on Site Characteristics of Strong Ground Motion[J].China Earthquake EngineeringJournal,2014,36(4):813-819.

Seismic Behavior of High Strength Steel Composite K-type Eccentrically Braced Frames with Direct Displacement-based Design Method

ZHENG Xiao-wei1, 2, SU Ming-zhou2, SHI Lu2, QIN Rui2, WANG Di-tao2, WANG Zhe3

(1.FacultyofImfrastructureEngineering,DalianUniversityofTechology,Dalian116000,Liaoning,China;2.SchoolofCivilEngineering,Xi’anUniversityofArchitectureandTechnology,Xi’an710055,Shaanxi,China;3.ChinaInstituteofBuildingStandardDesignandResearchCo.Ltd.,Beijing10048,China)

Links and braces use Q345 steel, while other structural members use high strength steel (e.g. Q460 steel). In particular, this is used in high strength steel combination eccentrically braced frames (HSS-EBFs), as it improves economic efficiency due to its weight and high strength. In this paper, in order to study their seismic performance, four groups of HSS-EBFs were designed using the direct displacement-based design (DDBD) method and included 5-, 8-, and 12-story structures. Nonlinear pushover analysis and dynamic elastoplastic analysis were performed on all designs, and inter-story drift and failure modes under rare earthquake events studied. The results show that the inter-story drifts satisfy the deformation requirement of the seismic code under rare earthquakes and the K-HSS-EBF structure presents an ideal progressively plastic mechanism, proving that this new design method is reasonable and reliable.

eccentrically braced frames; high strength steel; direct displacement-based seismic design; inter-story displacement; damage mode

2015-09-07

“十二五“科技支撑计划课题(2013BAJ10B03-0)

郑晓伟(1990-)男，山东人，博士，主要从事新型钢结构体系的抗震性能研究。E-mail:xwz217@163.com。

苏明周(1971-)，男，河南人，教授，博导，主要从事钢结构稳定与抗震、新型结构体系受力性能和设计理论研究。E-mail:sumingzhou@163.com。

TU392

A

1000-0844(2016)05-0678-07

10.3969/j.issn.1000-0844.2016.05.0678