飞翼无人机静气弹参数分析及操纵效率计算

许军, 马晓平

1.西北工业大学 航空学院, 陕西 西安 710072 2.中国电子科技集团公司第三十八研究所 浮空平台部，安徽 合肥 230088 3.西北工业大学 无人机所, 陕西 西安 710065



飞翼无人机静气弹参数分析及操纵效率计算

许军1,2, 马晓平3

1.西北工业大学 航空学院, 陕西 西安 710072 2.中国电子科技集团公司第三十八研究所 浮空平台部，安徽 合肥 230088 3.西北工业大学 无人机所, 陕西 西安 710065

耦合流体控制方程与结构动力学方程求解飞翼式无人机的静气动弹性参数响应及不同舵面的操纵效率。首先通过气动结构松耦合技术研究了飞翼无人机静气动弹性响应，对比分析刚性与弹性气动特，分析高度、马赫数、迎角及侧滑角对静气动弹性的影响；其次研究单一舵面偏转与组合舵面偏转的静气弹性，并分析结构几何非线性对静气动弹性的影响；然后分析阻力方向舵开裂角对静气弹的影响；最后计算不同马赫数不同舵面的操纵效率。研究表明迎角增大位移幅值也增大，不同高度位移响应频率形式是一样的，侧滑角对无人机半模静气动弹性响应并没有影响；开裂角增大位移幅值减小，且振荡收敛时间越短；方向舵操纵效率与组合舵面操纵效率相比差异较小，组合舵面操纵效率与单一舵面相比较高，不同组合舵面操纵效率比较接近。

飞翼无人机；静气动弹性；CFD/CSD；操纵效率；阻力方向舵；开裂角；弹性变形

飞翼式无人机成为无人机发展的一个重要方向。飞翼无人机设计中，气动弹性现象所引起的后续效应占有很重要的地位，新型飞翼无人机的一个突出特点就是大展弦比大柔性，这使得气动弹性问题也越来越复杂，因此需要对气动弹性现象进行深入的研究。对于大展弦比无人机的大型、柔性、轻质及变参数的结构特点，这使得非定常气动力与结构响应之间的耦合作用越来越复杂，非线性气动弹性现象更加突出。以往飞翼布局无人机设计过程中对于气动弹性的考虑都是采取刚性加弹性修正的方法，该方法得到的结果与实际的弹性飞机得到的结果有较大的差别。为减小气动弹性效应的影响，需发展高精度气动弹性计算方法对飞翼无人机气动弹性效应进行研究[1-3]。

安效民等[4]提出了一种界面映射推进技术，并应用于气动弹性中；Huo等[5]研究了弹性非结构动网格生成技术；刘学强等[6]提出一种动网格生成技术；杨国伟等[7]研究了静气动弹性效应的飞机外型的修正方法；王伟等[8]分析了考虑几何非线性太阳能无人机的静气动弹性；邵珂等[9]采用试验气动力技术研究了弹性飞机的舵面效率特性；Zhang等[10]研究了跨音速流中的控制面颤振效应；Cavagna等[11]研究了控制面机翼模型的气动弹性主动控制技术；杨超等[12]研究了多控制面飞机结构与配平的鲁棒气动弹性优化技术。

本文以大展弦比飞翼无人机为背景，基于气动结构松耦合技术研究飞翼无人机静气动弹性响应，对比分析刚性与弹性气动特性，研究高度、马赫数、不同开裂角等参数的影响；计算不同马赫数下不同舵面的操纵效率，分析无人机单一舵面与组合舵面的操纵效率。

1 CFD/CSD松耦合

工程通用的方法是松耦合技术，也就是独立求解结构动力学方程和气动控制方程，而仅仅在气动与结构的耦合界面上进行结构变形位移和气动力双向数据的传递，同时利用交错时间推进获得气动结构耦合计算的响应特性。

无人机的结构网格和气动网格划分往往是基于不同的原理，考虑到气动结构松耦合仅发生在气动与结构的耦合交界面上，因此在求解气动弹性问题时方程的耦合可由交界面的平衡条件与相容条件来引入的，气动弹性问题的基本方程如下：

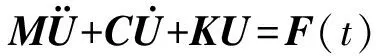
(1)

(2)

σs·n=-pn us=uF

(3)

(1)式为结构动力学方程；(2)式为积分形式的非定常N-S方程组；(3)式分别为交界面上的法向力平衡和位移相容条件；基于CFD/CSD松耦合技术，采用时间推进技术耦合求解方程(1)～(3)，开展飞翼无人机静气动弹性参数响应研究。

2 飞翼无人机

飞翼无人机静气动弹性计算时采用半模结构模型，如图1所示，机身结构为半硬壳式的，由横向隔框、纵向肋及上下蒙皮构成；内翼结构由壁板、大梁、翼肋组成；外翼由梁和肋组成，外翼后缘共有3个舵面：方向舵、副翼及升降舵。采用细网格建模有利于气动结构数据的高精度耦合传递，模型采用对称约束方式，飞翼无人机前四阶模态分别为6.36 Hz、22.032 Hz、29.155 Hz、64.455 Hz，CFD/CSD气动结构松耦合计算时的耦合面包括内机身、外机身、内翼、外翼、上阻力方向舵、下阻力方向舵、副翼、升降舵及襟翼。

图1 飞翼无人机模型

3 静气弹参数分析

首先采用CFD/CSD松耦合方法计算大展弦比飞翼式无人机的静气弹响应，计算状态为H=8km, Ma=0.6, Re=1.60×107，气动结构耦合计算时间步长为0.000 1 ，气动收敛误差为1×10-6，基于雷诺平均的N-S方程建立流体控制方程与结构动力学方程耦合求解方法，湍流模型采用SST湍流模型，基于LU-SGS子迭代的时间推进技术和HLLEW的空间离散方法进行求解，气动动网格变形采用弹簧近似光滑与局部网格重构方法，气动与结构耦合交界面精确匹配，并选取三维插值技术进行耦合界面结构变形位移与气动载荷数据间的传递。

图2给出了不同舵面静气动弹性计算的位移和加速度响应。其中图2a)为无人机不同舵面的位移响应，从图中可看出方向舵位移响应幅值较大，襟翼位移响应幅值最小，而副翼与升降舵的位移幅值居中，这主要是由于与机身根部的距离而决定的，因为方向舵距离机身根部最远；对比振荡收敛时间也可发现：方向舵振荡收敛所需设计最长，而副翼、升降舵与方向舵位移曲线相比收敛时间较快，进入收敛平衡状态的时间也越短。图2b)给出不同舵面的加速度响应，从图中可看出方向舵的加速度响应比较剧烈，而襟翼的加速度响应最不剧烈，且副翼和升降舵次之。

图2 不同舵面响应

表1为采用CFD/CSD松耦合计算的刚性与弹性无人机模型的气动特性，其中刚性静气动弹性的气动特性计算指的是气动结构松耦合第一个迭代步的计算结果；弹性静气动弹性的气动特性指的是气动结构松耦合计算收敛的计算结果。对比相同计算状态下的刚性体与弹性体可发现：气动结构松耦合弹性计算的升力系数和阻力系数，这主要是因为气动结构松耦合计算中考虑了结构弹性变形对气动特性的影响；而弹性俯仰力矩系数较刚性相比有所增大(俯仰力矩系数不考虑正负，俯仰力矩系数正负表示其方向)。

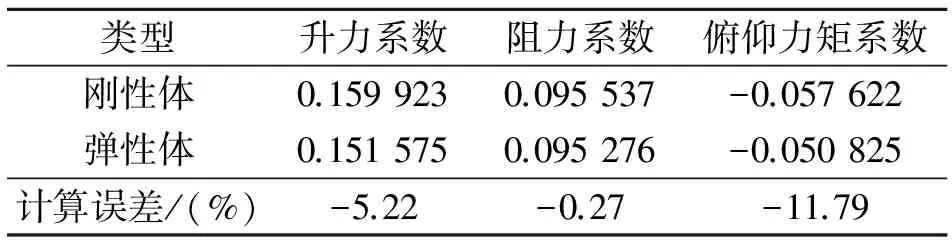
表1 刚性/弹性气动特性

图3给出了不同参数下方向舵静气动弹性响应。图3a)为不同迎角下方向舵位移响应，从图中可看出随着迎角的增大，舵面位移收敛幅值也增大，这是因为迎角增加，无人机机翼的气动载荷也增加，随着迎角的增大，位移响应进入收敛平衡状态所需的时间也越长。图3b)为不同高度下不同舵面的位移响应曲线，从图中可看出不同高度下位移响应的频率形式是一样的，不同在于响应幅值的不同，主要是由于无人机在同马赫数不同高度时，其飞行动压是不一样的，从而引起位移响应幅值的不同。飞行高度越高位移响应的幅值越小，而飞行高度越低位移响应的幅值越大。对比收敛的时间可看出：高度越高位移响应收敛进入平衡状态所需要的时间也会越长，振荡越剧烈。这也主要是由于动压的不同而造成的，高度越高动压越大，从而气动力与结构弹性变形之间的耦合作用越强，就会导致气动与结构相互耦合作用达到平衡时所需要的时间也越多，即从位移响应开始到收敛所需要的时间也就越来长。图3c)为不同马赫数下静气动弹性计算中不同舵面的位移响应。对比不同马赫数状态的位移响应可发现：0.6Ma时不同舵面的位移整体幅值最大，而0.5Ma时位移的整体幅值最小；且0.7Ma时位移收敛所需要的时间最长。图3d)为不同侧滑角时舵面的位移响应，从图中可看出侧滑角对舵面位移响应并没有影响。这主要是因为本文静气动弹性耦合计算中采用的半模，侧滑角对无人机半模静气动弹性响应并没有影响。

图3 静气弹参数分析

4 舵偏静气弹分析

图4为不同舵面偏转模型的位移响应，从图中可看出：无舵面偏转模型与其他舵偏模型相比静气动弹性的位移幅值较大；方向舵偏转4°与升降舵偏转及襟翼偏转相比位移相比都较大。

图5和图6分别给出了方向舵偏转4°和全舵偏4°下不同参数下静气动弹性响应，图5a)为不同马赫数的位移响应，从图中可看出：随着马赫数的增加，舵面位移响应幅值有所增大，这是因为不同马赫数下动压不同，且马赫数越大，飞行动压也增加，气动结构耦合计算也越剧烈。图5b)为方向舵偏转4°不同高度的位移响应，从图中可看出：随着高度的增加，舵面位移响应幅值有所减小，这是因为不同高度下动压不同，且高度越大，飞行动压越小。

图4 不同舵偏方向舵位移

图5 方向舵偏4°静气弹响应图6 全舵偏4°静气弹响应

图7为不同组合舵面偏转模型方向舵位移响应，从图中可看出：无舵面偏转和方向舵单一偏转模型与组合舵偏模型相比静气动弹性的位移和加速度幅值较大。

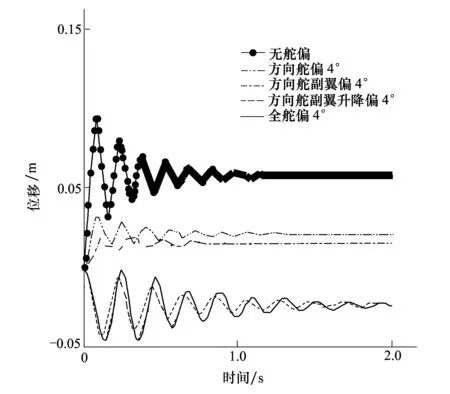
图7 组合舵偏模型方向舵静气弹响应

图8给出了无舵面偏转方向舵的线性与非线性的位移和加速度响应，其中非线性是气动结构松耦合计算中考虑结构几何非线性。从图中可看出考虑结构几何非线性后外翼前缘的位移响应幅值有所减小。

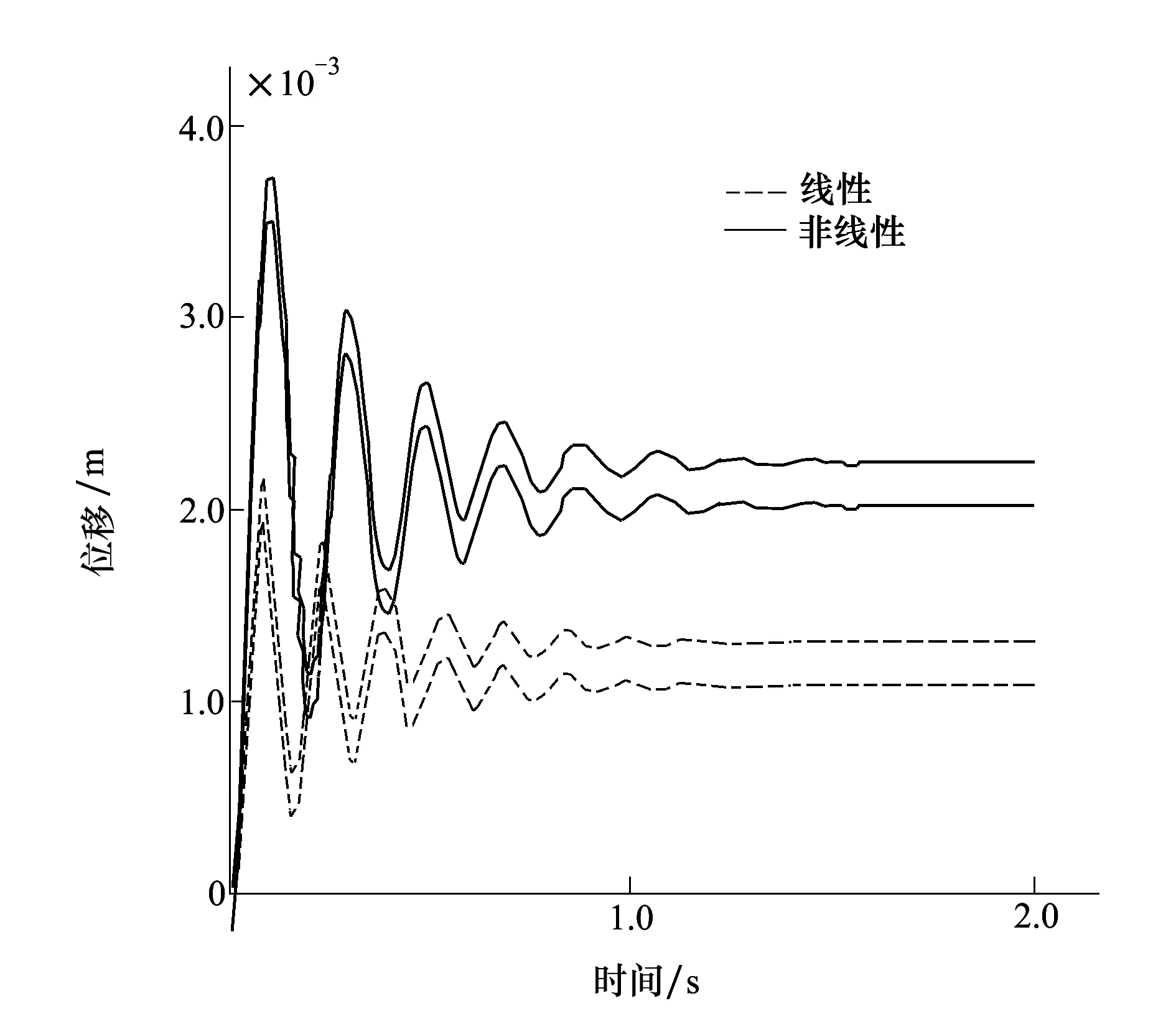
图8 无舵偏方向舵响应

图9给出了单一舵偏模型和组合舵偏下方向舵的线性与非线性位移响应，从图中可看出考虑结构几何非线性后位移幅值有所减小。

图10为不同阻力方向舵开裂角模型方向舵位移响应，其中图10a)为线性位移响应，图10b)为线性与非线性位移对比图；从图中可看出随着开裂角的增大，方向舵位移响应幅值有所减小；且振荡收敛所需的时间也越短；考虑结构几何非线性后位移幅值有所减小。

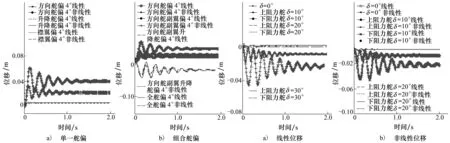
图9 不同舵偏方向舵位移图10 不同开裂角下方向舵位移

5 舵面操纵效率分析

本节采用气动结构松耦合技术分析飞翼无人机不同飞行速度不同舵面下的操纵效率，其中操纵效率计算公式是计算舵面偏转后，考虑弹性变形的无人机俯仰力矩系数的增量与刚性无人机俯仰力矩系数增量之比，通过改变来流速度可以计算不同马赫数下不同舵面的操纵效率。

(4)

式中,Cmeδ为偏转δ角度后弹性无人机的俯仰力矩系数,Cmrδ为偏转δ角度后刚性无人机的俯仰力矩系数，Cme0为无舵偏弹性无人机俯仰力矩系数，Cmr0为无舵偏刚性无人机俯仰力矩系数。

表2给出了不同舵偏模型下计算的无人机刚性与弹性俯仰力矩系数。对比同一模型的刚性与弹性俯仰力矩系数可发现：基于CFD/CSD松耦合计算的弹性俯仰力矩系数与刚性相比较大；不同舵面模型与无舵偏模型相比俯仰力矩系数增大。

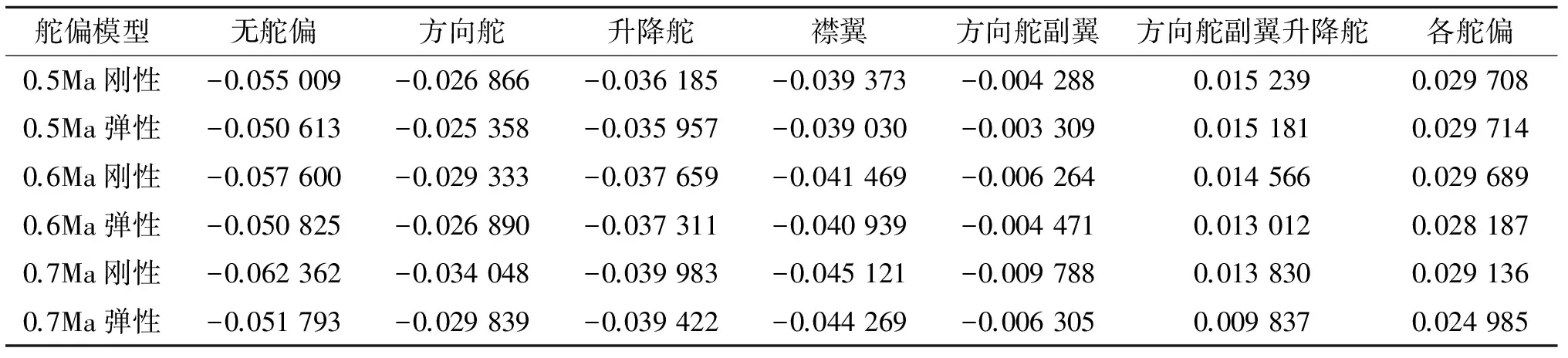
表2 不同模型刚/弹性俯仰力矩系数

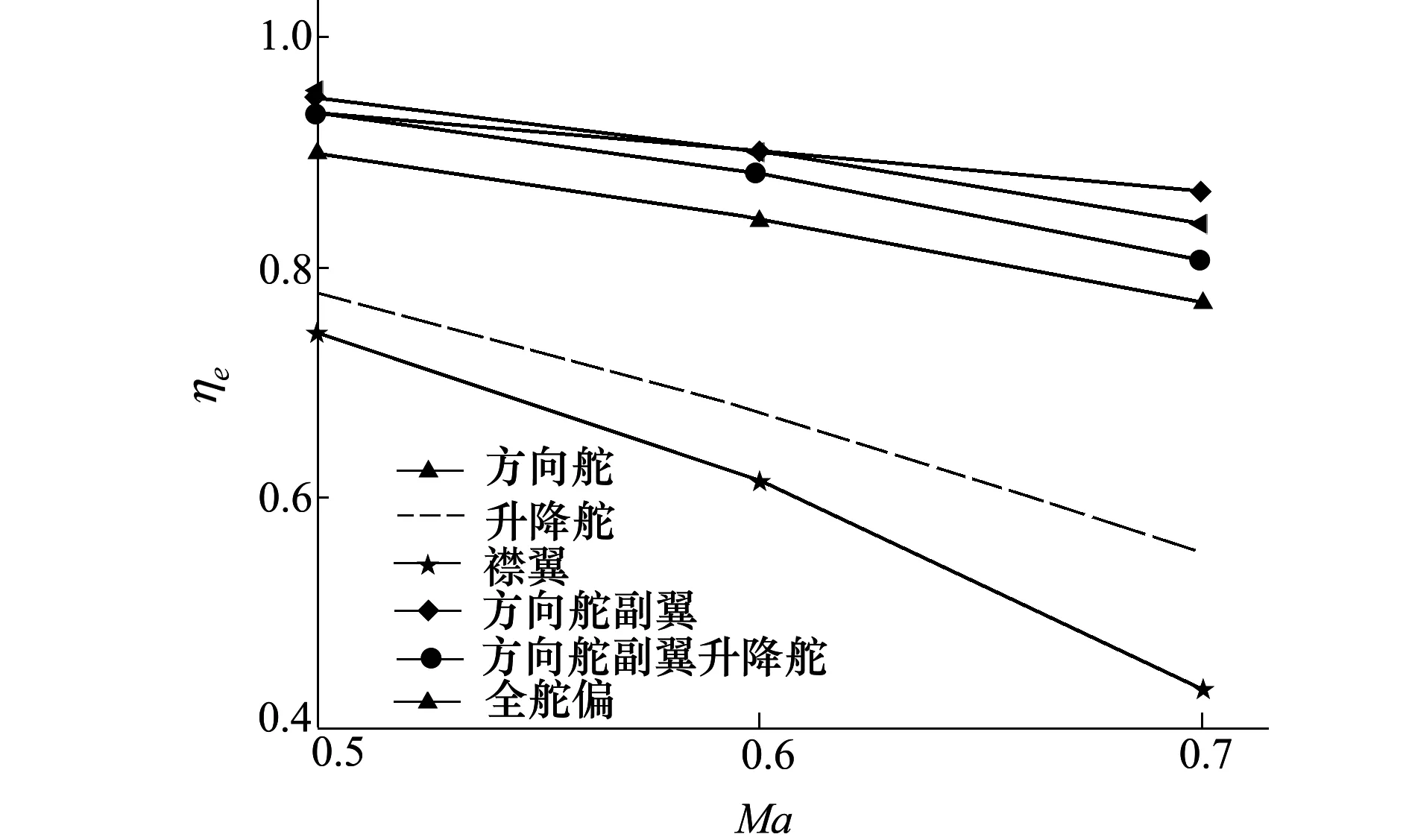
图11 不同舵面操纵效率

基于表2所示的俯仰力矩系数可计算不同马赫数不同舵面的操纵效率，如图11所示，从图中可看出：随着马赫数增加，不同舵面的操纵效率整体呈现减小的趋势；单一舵面偏转操纵效率比较发现：方向舵与升降舵、襟翼相比操纵效率最高，襟翼的操纵效率最低，且方向舵操纵效率与组合舵面操纵效率相比差异较小；组合舵面偏转操纵效率与单一舵面相比较高，且不同飞行马赫数下不同组合舵面操纵效率比较接近，在0.7Ma时全舵面偏转引起的操纵效率与方向舵副翼组合舵面相比操纵效率减小。

6 结 论

本文通过气动结构松耦合技术研究了飞翼无人机静气动弹性，研究单一舵面偏转与组合舵面偏转的静气动弹性特性，分析高度、马赫数、迎角及侧滑角对静气动弹性响应的影响，分析不同阻力方向舵开裂角对静气动弹性和操纵效率的影响，得到以下结论：

1)随着迎角的增大，舵面位移收敛幅值也增大；不同高度下位移响应的频率形式是一样的，不同在于响应幅值的不同；侧滑角对无人机半模静气动弹性响应并没有影响。

2)无舵面偏转和方向舵单一偏转模型与组合舵偏模型相比静气动弹性的位移幅值较大。

3)阻力方向舵开裂角的增大，方向舵位移响应幅值有所减小；且振荡收敛所需的时间也越短。

4)方向舵操纵效率与组合舵面操纵效率相比差异较小；组合舵面偏转操纵效率与单一舵面相比较高，且不同飞行马赫数下不同组合舵面操纵效率比较接近。

[1] 杨佑绪, 吴志刚, 杨超. 飞翼结构构型气动弹性优化设计方法[J]. 航空学报, 2013, 43(12): 2748-275

YangYouxu,WuZhigang,YangChao.AnAeroelasticOptimizationDesignApproachforStructuralConfigurationofFlyingWings[J].ActaAeronauticaetAstronauticaSinica, 2013, 43(12): 2748-2756 (inChinese)

[2]XuJun,MaXiaoping.TransonicRudderBuzzonTaillessFlyingWingUAV[J].TransactionsofNanjingUniversityofAeronautics&Astronautics, 2015, 32(1): 61-69

[3] 许军, 马晓平. 飞翼无人机嗡鸣气动弹性响应分析[J]. 西北工业大学学报, 2015, 33(4): 588-595

XuJun,MaXiaoping.BuzzAeroelasticResponsesAnalysisforaFlyingWingUAV[J].JournalofNorthwesternPolytechnicalUniversity, 2015, 33(4): 588-595 (inChinese)

[4] 安效民, 徐敏, 陈士橹. 一种新的界面映射推进方法及其在气动弹性力学中的应用[J]. 宇航学报, 2009, 29(5): 1472-1479

AnXiaomin,XuMin,ChenShilu.ANewInterfaceMappingandMarchingMethodforAeroelasticity[J].JournalofAstronautics, 2009, 29(5): 1472-1479 (inChinese)

[5]HuoShihui,WangFunsheng,YanWuzhu,YueZhufeng.LayeredElasticSolidMethodfortheGeneratingofUnstructuredDynamicMesh[J].FiniteElementsinAnalysisandDesign, 2010, 46(10): 949-955

[6] 刘学强, 李青, 蔡建忠, 等. 一种新的动网格方法及应用[J]. 航空学报, 2008, 29(4): 817-822

LiuXueqiang,LiQing,ChaiJianzhong,etal.ANewDynamicGridAlgrithmandItsApplication[J].ActaAeronauticaetAstronauticaSinica, 2008, 29(4): 817-822 (inChinese)

[7] 杨国伟, 郑冠男. 基于静气动弹性效应的飞机型架外形修正方法研究[J]. 航空工程进展, 2011, 2(2): 143-150

YangGuowei,ZhengGuannan.AircraftJigShapeCorrectionMethodBasedonStaticAeroelasticAnalyes[J].AdvancesinAeronauticalScienceandEngineering, 2011,2(2): 143-150 (inChinese)

[8] 王伟, 周洲, 祝小平, 王睿. 考虑几何非线性效应的大柔性太阳能无人机静气动弹性分析[J]. 西北工业大学学报, 2014, 32(4): 499-504

WangWei,ZhouZhou,ZhuXiaoping,WangRui.StaticAeroelasticCharacteristicsAnalysisofaVeryFlexibleSolarPoweredUAVwithGeometricalNonlinearEffectConsidered[J].JournalofNorthwesternPolytechnicalUniversity, 2014, 32(4): 499-504 (inChinese)

[9] 邵珂, 万志强, 杨超. 基于试验气动力的弹性飞机舵面效率分析[J]. 航空学报, 2009, 30(9): 1612-1617

ShaoKe,WanZhiqiang,YangChao.ControlSurfacesEfficiencyAnalysisofFlexibleAircraftBasedonExperimentalAerodynamicForces[J].ActaAeronauticaetAstronauticaSinica, 2009,30(9): 1612-1617 (inChinese)

[10]ZhangWeiwei,YeZhengyin.EffectofControlSurfaceonAirfoilFlutterinTransonicFlow[J].ActaAstronautic, 2010, 66(7/8): 999-1007

[11]CavagnaL,RicciS,ScottiA.ActiveAeroelasticControloveraFourControlSurfaceWingModelAerospace[J].ScienceandTechnology, 2009, 13(7): 374-382

[12] 杨超, 肖志鹏, 万志强. 多控制面飞行器结构与配平鲁棒气动弹性优化方法[J]. 航空学报, 2011, 31(1): 75-82

YangChao,XiaoZhipeng,WanZhiqiang.ARobustAeroelasticOptimizationMethodofStructureandTrimforAirVehiclewithMultipleControlSurfaces[J].ActaAeronauticaetAstronauticaSinica, 2011,32(1): 75-82 (inChinese)

Flying Wing UAV Static Aeroelastic Parameter Analysis and Control Efficiency Calculation

Xu Jun1,2, Ma Xiaoping3

1.College of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China 2.Department of Aerostat Platform, No. 38 Research Institute of CETC, Hefei 230088, China 3.UAV Research Institute, Northwestern Polytechnical University, Xi′an 710065, China

The flying wing UAV static aeroelastic parameters responses and different rudders control efficiency, based on the fluid control equation and structural dynamics equation coupling model, were solved. Firstly the flying wing UAV static aeroelastic responses based on the aerodynamic structural loosely coupling method were studied, the rigid and elastic aeordynamic characteristic were analysis, the effect of height, Mach numbers, attack angle, sideslip angle on the static responses were also analysis. Secondly the single rudder and combination rudders deflection static aeroelastic were given, and the linear and nonlinear on the static aeroelastic responses were also studied. And then effect of rudder crack initiation angles on the static aeroelastic were given; Finally different rudders control efficiency at different Mach numbers were calculated. The research results showed that: (1) the displacement amplitude increased as the attack angle increased, the displacement response frequency was the same at different heights, and the sideslip angle had no effect on the UAV semi model static aeroelastic responses; (2) the displacement amplitude decreased as the cracking angle increased, and the oscillation convergence time was shorter; (3) the rudder control efficiency were closed to the combination rudders control efficiency, which had higher control efficiency compared with the single rudder, and the different rudders control efficiency were almost the same.

flying wing UAV; static aeroelasticity; CFD/CSD; control efficiency; drag rudder; crack initiation angle; elastic deformation

2016-03-17

陕西省自然科学基金(2013JM015)资助

许军(1987—)，西北工业大学工程师，主要从事无人机总体及气动弹性的研究。

V211.5

A

1000-2758(2016)05-0747-07