多组件结构系统布局拓扑优化中处理组件干涉约束的惩罚函数方法
朱继宏, 郭文杰, 张卫红, 何飞
西北工业大学 工程仿真与宇航计算技术实验室, 西安 710072
多组件结构系统布局拓扑优化中处理组件干涉约束的惩罚函数方法
朱继宏*, 郭文杰, 张卫红, 何飞
西北工业大学 工程仿真与宇航计算技术实验室, 西安 710072
包含大量组件的多组件结构系统布局拓扑优化设计中存在大量的组件干涉约束,研究了包含大量组件的结构系统整体式拓扑布局优化设计问题,基于有限包络圆方法(FCM)提出了处理组件干涉约束的惩罚函数方法,构造了包含结构刚度和组件之间几何干涉函数的内外混合惩罚函数,应用基于梯度的优化算法对包含数十个组件上百个干涉约束的多组件结构系统进行刚度优化设计,得到了清晰的支撑结构构型和无干涉的组件布局位置,充分体现了提出的混合惩罚函数方法在解决多组件结构系统布局拓扑优化设计中组件干涉问题上的有效性和适用性。
拓扑优化; 多组件结构系统; 混合惩罚函数; 干涉约束; 有限包络圆法
结构拓扑优化设计技术经过近30年的发展和完善,已经逐步成为概念设计阶段的一个重要方法。到目前为止,拓扑优化技术在科学研究及工程应用领域都取得了显著成就,已成为航空航天结构设计中减轻结构重量、提高系统性能的关键技术手段之一。随着飞行器性能的不断提高,飞行器结构系统变得越来越复杂,飞行器需要搭载的设备也越来越多。与图1所示的典型多组件结构系统示意图相似,大多数飞行器结构系统都可以看做是多个设备(称组件或特征)以一定的支撑连接方式与主承力结构进行连接而构成的多组件结构系统。

图1 典型多组件结构系统示意图Fig.1 Illustration of a typical multi-component system
多组件结构系统拓扑布局优化的本质是实现组件的空间布局及其支撑结构构型的协同优化设计,将组件从有效载荷转化为承力件参与到传力路径布局中,实现组件、结构的整体式设计。前期相关学者已开展了大量有益的工作,如Chicker-mane[1]、Li[2]和Ma[3]等将多组件结构系统中互相分离的部分看做不同设计区域中的多种组件,组件的结构构型和支撑组件的连接位置通过基于密度点的拓扑优化方法实现协同优化;Zhu等[4-7]提出了基于密度点法的多组件结构系统拓扑布局协同优化技术,实现了组件的空间布局与支撑结构拓扑构型的协同设计;张卫红等[8]近期提出了部件级多组件结构系统的整体式布局优化设计,实现了组件、部件位置与支撑结构的协同优化。图2给出了典型多组件结构系统布局优化的示意图。
多组件结构系统协同优化面临的主要挑战之一是如何有效避免不同组件之间的干涉问题。组件数目过多会导致组件之间干涉约束函数的非线性程度增加,使求解变得困难。为了解决这种干涉问题,学者们提出了运用如八叉树法(Octrees)[9-10]、球体树法(Sphere Trees)[11]以及基于S边界树法(S-bounds Based Trees)[12]等方法判断不同组件之间的干涉重叠,不同组件的轮廓用一系列不同尺度的立方体或球体近似描述,然而这些方法的局限性在于其只能检测干涉而无法计算干涉,这样就无法判断优化问题的寻优方向,也就很难获得最优解。因此,现有工作大多采用无需灵敏度分析的遗传算法[13]和蚁群算法[14]等启发式算法来研究包含系统质心[13,15]和转动惯量[16]等物理约束的空间装填布局问题。
随后,基于梯度优化算法的一些方法被相继提出,如Zhang 和 Zhu 等[17]提出了有限包络圆方法(Finite Circle Method, FCM),这种方法可以获得组件之间干涉约束函数的灵敏度,在有限包络圆方法中,组件轮廓用一系列包络圆近似描述(三维组件为包络球),通过约束包络圆之间的不干涉实现组件之间的不干涉。这种方法虽然可以解决组件之间的干涉问题,但是会引入大量的干涉约束函数,尤其在组件数目很多的情况下,由于干涉约束函数的非线性程度增加,保证组件之间不发生干涉十分困难,对于约束函数数目较多的优化问题,相关学者通过一定的约束凝聚方式进行处理,如P-norm函数、KS函数法[18]等。但是对于非线性程度很高的问题,约束凝聚也存在一定的局限性。除有限包络圆方法外,单鹏[19]、Kang和Wang[20]提出水平集(Level-set)方法,该方法通过积分运算强制约束组件之间的干涉区域面积为0以保证组件之间不发生干涉。

图2 多组件结构系统布局优化示意图 Fig.2 Illustration of integrated layout and topology optimization of a multi-component system
早期关于罚函数的研究工作是将带约束优化问题转化为无约束优化问题进行求解,例如Courant[21]在1943年提出用罚函数求解微分方程。20世纪60年代,Fiacco和Mccormick[22]提出了混合罚函数,用来求解包含等式、不等式的约束优化问题,扩大了罚函数的应用范围。Chen等[23]用混合罚函数修正了鸡群算法(Chicken Swarm Optimization, CSO),解决了带约束优化问题。Huang[24]、Jayswal[25]和Yu[26]等用不同形式的罚函数求解了带约束优化问题。
在此基础上,本文提出应用混合罚函数方法解决多组件结构系统布局优化设计中组件之间相互干涉的问题,应用有限包络圆方法描述组件的外形轮廓,组件与其支撑结构之间的连接用多点约束技术(Multi-point Constraints,MPC)模拟[27],通过罚函数将包含大量干涉约束的优化问题转化成无干涉约束的优化问题,以结构的整体刚度最大为目标对多组件结构系统进行协同优化设计。
1 优化设计模型定义
1.1 基于罚函数的干涉约束处理
前期学者的工作已经表明,有限包络圆方法在多组件结构系统布局优化设计中,可以很好地解决组件之间的干涉问题。事实上,要尽可能准确地描述组件的外形需要定义大量的包络圆,这样势必会导致干涉约束函数数目的增加,干涉约束函数的非线性程度也随之增加,基于梯度的优化算法很难实现对各个干涉约束函数的有效约束。
考虑式(1)所示形式的包含不等式约束的最优化问题。
(1)
式中:f(x) 为优化目标函数;x为优化问题设计变量;ci(x)为第i个优化约束函数。
根据最优化方法理论[27],这里不加证明地给出上述约束最优化问题的外惩罚函数形式为
minp(x,σ)=f(x)+
(2)
式中:σ为外惩罚因子。同样地,该约束最优化问题对应的内惩罚函数可以写为
(3)
式中:κ为内惩罚因子。
不同的是,外惩罚函数所求得的最优解大多是从原优化问题可行域外部趋向于可行域边界的解,内惩罚函数的寻优范围必须在可行域内部。两种构造方式各有利弊,外惩罚函数可以求解一般约束问题,但无约束优化问题的最优解往往是可行域外部趋于可行域边界的解。内惩罚函数只能求解不等式约束优化问题,但能保证无约束优化问题的最优解严格落在可行域内。
事实上,上述惩罚函数构造方式有时在求解时面临一些困难。一方面,原优化问题的目标函数与约束函数的数量级不同,构造的无约束最优化问题的性态很难保证,如果原目标函数的数量级远远大于约束函数,那么约束的影响就会很小,极易导致约束无法满足,反之如果约束函数的数量级很大,则原目标函数极有可能被覆盖掉,导致优化无法进行。
本文中对惩罚函数进行改进,针对多组件结构系统布局优化设计方法,提出了新的归一化的惩罚函数方法。考虑由有限包络圆方法引入的干涉约束函数:
(4)

这里先给出由干涉约束函数构造的惩罚函数的惩罚项(见式(5)),包含结构应变能的无干涉约束最优化问题的目标函数稍后给出。
(5)
式中:第1个式子右端前后两项分别记为外、内惩罚项;α和β分别为外、内惩罚因子;ri0和sj0分别为ri和sj对应的初始值(初始值为非零可行解)。在惩罚函数范围变化不大的情况下,通过上述变换可以有效避免因干涉约束函数数量级不匹配带来的病态问题。其中l1为所有非正的干涉约束函数的数目,m为干涉约束的总数目,在优化过程中,每次迭代需要对干涉约束函数进行判断,对于非正的干涉约束函数采用外惩罚处理,对于大于0的干涉约束函数用内惩罚处理。事实上,外惩罚项的作用是,当干涉约束非正时,增大惩罚项值以使目标增大,通过优化算法将约束向可行域内拉近,一旦约束函数跳入可行域内,在内惩罚项的作用下,越接近可行域边界的函数受到的障碍作用越大,越不易逃离可行域,以此实现对各个干涉约束的有效控制。有必要指出,惩罚因子的选取对计算结果的好坏有重要影响,惩罚因子太大或太小都有可能得不到合适的最优解,本文给出适用于本优化问题的惩罚因子初始值,并定义迭代格式,使惩罚因子在给定的范围内迭代。

图3 多组件结构系统的有限包络圆划分示意图Fig.3 Illustration of approximation of a multi-component system by finite circle method (FCM)
αt+1=2αt,t=1,2,…,iter,α1=1
(6)
βt+1=2βt,t=1,2,…,iter,β1=10 000
(7)
迭代终止的条件是相应的外、内惩罚项落在各自的控制误差ε(ε=0.000 1)内。t为迭代步次,iter为迭代进行的总次数。给定外、内惩罚因子的上限分别为10和106。
1.2 系统质心位置约束
本工作引入系统质心位置约束。对于多组件结构系统而言,通过杠杆原理可以得到系统的质心位置为
(8)
式中:mε和mi分别为组件ε和设计域单元i的质量;[xGyGzG]T、[xGεyGεzGε]T和[xGiyGizGi]T分别为系统、组件及设计域单元的质心位置。
式(8)变形可得
(9)
对于给定的多组件结构系统,质心位置约束可以写为
(10)
式中:ai、bi(i=1,2,3)构成了相应坐标分量在全局坐标系下的变动范围。
1.3 优化模型
应用多点约束技术模拟组件与其支撑结构之间的刚性连接,多点约束技术引入的多点约束方程是节点位移的线性组合,多个多点约束方程和边界条件方程可以统一写为
Hu=0
(11)
式中:H为由结构单元的形状函数、多点约束位置和边界条件共同决定的系数矩阵;u为多组件结构系统的整体位移向量。
考虑多点约束方程,修订后的系统势能可以写为

(12)
式中:K和u分别为结构整体刚度矩阵和位移向量;F和λ分别为节点载荷和拉格朗日乘子向量。驻点处的欧拉公式可以写为
(13)
求解式(13)可以得到u和λ。
优化过程中,需要考虑组件布局、结构拓扑构型这两类设计变量,即
(14)
式中:(xε,yε,θε)为描述组件ε位置的几何设计变量,包括平动及转动坐标;ηi为主结构设计域单元i的伪密度设计变量;nca和nda分别为组件数目、结构拓扑设计域单元数目。应用Zhu和Zhang[7]提出的多项式插值模型对设计域结构进行拓扑优化设计。
(15)
式中:mi和Ei分别为拓扑设计域单元i的质量和弹性模量;mi0和E0分别为设计域单元i满材料时的质量和弹性模量。本文分别取γ和τ为16和4。
记系统的应变能函数为C=(uTKu)/2,初始应变能记为C0,引入提出的惩罚函数后,优化目标包含应变能函数及组件干涉约束函数,构造如式(16)所示的目标函数。
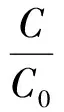
(16)
式中:等号右端第1项,将应变能函数与系统初始应变能作比值,将其转化为无量纲的量,比值取到极小值时,系统应变能也取到极小值。包含系统应变能和惩罚项的目标函数将原来的含有组件干涉约束的约束最优化问题转化为无组件干涉约束的最优化问题求解,避免了分别约束各个干涉约束函数导致的因约束函数非线性程度过大而无法实现有效约束的问题,当惩罚因子取得合适的值时,式(16)的极小值就是其对应的等号右端第1项的极小值[28]。
引入多点约束技术的多组件结构系统满足的约束条件为
(17)
式中:V和VU分别为结构材料用量及其上限;Γε和ΓD分别为组件及设计域所占空间。
2 灵敏度求解
2.1 惩罚函数灵敏度求解
首先推导无组件干涉约束的目标函数P对结构构型拓扑优化伪密度设计变量的灵敏度。
式(16)两端同时对拓扑设计单元伪密度设计变量求偏导可得:

(18)
式中:C0为常数,易知由干涉约束函数构成的惩罚项对伪密度设计变量的灵敏度∂Q/∂ηi=0,因此,只要求出系统应变能函数对伪密度设计变量的灵敏度并代回式(18)即可。
式(13)中第1式两端同时对伪密度设计变量求偏导可得:
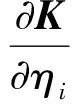
(19)
假设F=f+G,其中f为设计无关载荷,G为设计相关载荷,如重力、惯性力、离心力等。设计无关载荷f对伪密度设计变量的灵敏度为0,因此式(13)中第1式可以简化为
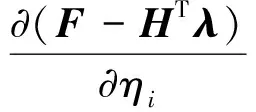
(20)
结构总体应变能可以表达为

(21)
联立式(19)~式(21),应变能对伪密度设计变量ηi的灵敏度可以写为

(22)
根据已知的∂HT/∂ηi=0,可以得到:

(23)
由于uTHT=0,故式(23)可以简化为

(24)
式(24)中设计相关载荷G和整体刚度矩阵K可根据材料质量和材料插值模型求得。结构整体位移向量u可以通过一次有限元分析得到。将式(24)代入到式(18)可以求得:
(25)
式(16)两端同时对组件平动几何设计变量ξi求偏导得:
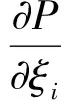
(26)
先求应变能函数对组件几何设计变量的偏导,可得:
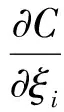
(27)

(28)
由∂F/∂ξi=0,uTHT=0,可以得到:
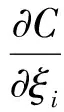
(29)
假设ξi是第i个组件的平动坐标设计变量,由于在有限元分析过程中组件平动不会影响总体刚度矩阵,可知∂K/∂ξi=0,这样式(29)就可以简化为
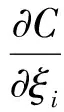
(30)
如果ξi是第i个组件的转动坐标设计变量,则当组件在有限元分析过程中发生转动时,组件的刚度矩阵可以写为
(31)

(32)
最终,系统总体应变能对转动设计变量的灵敏度可以写为
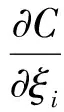
(33)
系统的应变能函数对组件几何设计变量的灵敏度可以统一写为
(34)
惩罚项Q对组件几何设计变量的灵敏度可以根据有限包络圆方法很容易地求得,联立式(34)代回到式(26)中即可。
2.2 质心位置约束灵敏度求解
式(8)两端同时对第i个设计域单元的伪密度设计变量ηi求偏导,可得
(35)
式(35)变形可得
(36)
将式(15)代入到式(36)可得
(37)
类似地,系统质心位置对组件位置几何设计变量的灵敏度可以很方便地求解。需要指出的是,本工作中,由于组件的转动中心及平动参考中心定义在组件质心上,因此,组件转动不会改变组件的质心位置。这样一来,系统质心对组件转动几何设计变量的灵敏度即为0。假定ξi是某个组件的一个平动位置设计变量,那么式(8)两端同时对ξi求偏导可得
(38)
式(38)中,如果ξi=xG ε,则式(37)可以写为
(39)
同样道理,如果ξ=yGε,则式(38)可以写为
(40)
本工作中,组件只在xOy平面内运动,故组件的运动对整个系统z向质心分量无影响。
2.3 其他约束函数的灵敏度求解
对于设计域材料用量约束,其对伪密度设计变量的灵敏度为常数,对各组件几何设计变量的灵敏度均为0。
3 数值算例
3.1 包含3个组件的悬臂梁结构系统

图4 悬臂梁结构系统示意图Fig.4 Illustration of cantilever system
考虑如图4所示的悬臂梁结构,3个组件在设计区域内按图布置,拓扑设计域为1.5 m×0.6 m 的矩形区域,厚度为0.02 m,左端上、下施加边界条件,各固定一段长度为0.08 m的区域,下端在距固定端0.75 m、1.50 m处均施加水平向右、竖直向下的1 kN的集中力。设计域内,按图4所示安放3个组件(组件尺寸如图5所示),每个组件与设计域之间通过多点约束技术建立刚性连接,图6给出了组件的有限包络圆近似及组件与设计域建立连接的位置。设计区域及组件的材料属性如表1所示。
首先应用传统的分别约束组件之间各个干涉约束函数的方法对上述系统进行布局优化设计,要求整体刚度最大,使组件之间满足非干涉要求,约束设计区域材料用量比的上限为0.4,组件在系统中的初始布局如图4所示,经过120次迭代,优化问题收敛,系统应变能C=0.051 J。最终所有组件之间均未发生干涉。图7直接给出了最终的优化结果。
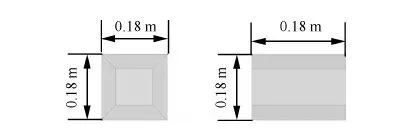
图5 悬臂梁结构系统组件尺寸Fig.5 Size of components in cantilever system
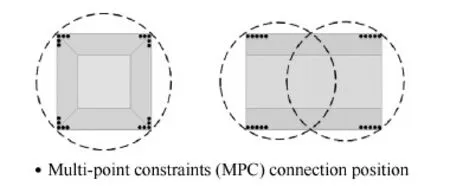
图6 组件有限包络圆描述Fig.6 Approximation of components by FCM

表1 悬臂梁结构的材料属性Table 1 Material properties of cantilever system

图7 用传统约束处理方法得到的优化结果 Fig.7 Optimized design using standard method for dealing with constraints
随后,应用本文提出的方法,对上述结构系统重新进行布局优化设计,图8给出了结构的优化迭代历史。
图9给出了上述两种方法的优化过程收敛曲线。
对比分别约束各干涉约束函数与应用本文提出的惩罚函数方法求得的结果可发现,两者拓扑设计域构型相似但不完全相同,均形成了合适的传力路径,组件作为承力件合理地布置在设计域内。

图8 优化迭代历史Fig.8 Iteration history of optimization

图9 两种方法的优化过程迭代曲线Fig.9 Convergence history of optimization by above two methods
优化过程中,应用惩罚函数方法计算的应变能变化平稳,而传统的分别约束各个干涉约束函数的方法计算的应变能跳动较大,两者最终都收敛,优化结果显示两种方法计算的系统应变能相差不大,相对误差为3%。可见,本文所提方法是有效可行的。
为了进一步验证方法的适用性,仍以上述悬臂梁为拓扑设计域,用本文所提方法处理组件之间的干涉约束,初始将各组件干涉布置,各组件的初始布局如图10所示,其中虚线部分表示组件之间的干涉区域。这里,由于算法要求各个干涉约束的初始值均为可行解,故仍以第1组算例中各个干涉约束函数的初始值作为本次计算的初始值。图11给出了此初始条件下优化问题的设计结果。
如图12所示,经过88次迭代,系统应变能函数收敛于0.048 J,由于初始组件是干涉的,在前4步迭代中,组件只在自身位置只发生微小扰动,从第5步开始,在惩罚函数的驱动下,组件逐渐分开,图12中给出了第5~10步迭代的组件布局,从第10步开始,描述组件的包络圆之间已经完全没有干涉,后续迭代中组件仍然保持着互不干涉。可见,本文所提的约束处理方法能有效避免组件之间的干涉。
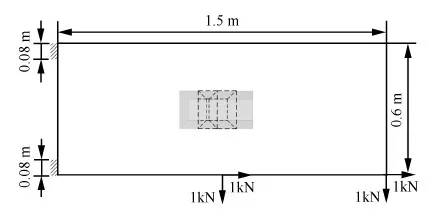
图10 组件初始干涉工况示意图Fig.10 Illustration of system with original overlapped components
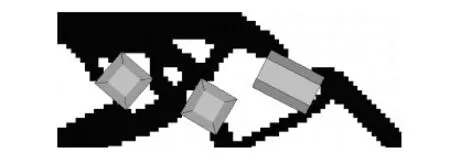
图11 组件初始干涉的优化结果 Fig.11 Optimized design of system with original overlapped components
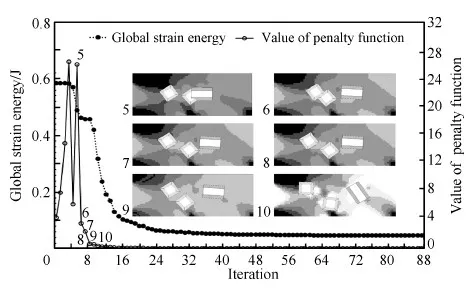
图12 组件初始干涉的优化过程迭代曲线Fig.12 Convergence history of optimization of system with original overlapped components
3.2 包含24个组件的简化挂架结构系统
以一个24组件的简化挂架结构系统为例,进一步验证所提方法在解决多组件结构系统布局优化问题中的适用性。多组件结构系统布局优化设计中,当干涉约束数目增多时,传统的约束处理方式将不再实用,这里所有组件之间的干涉约束函数数目为484个,传统的处理干涉约束的方法已经很难有效地解决这一问题。
图13给出了简化挂架结构系统的工况示意,一个长、宽、厚度为2.25 m×1.55 m×0.02 m的简化挂架,以挂架左下角点为坐标原点建立坐标系,x轴正向水平向右,y轴正向竖直向上。挂架左端完全固定,右上角施加竖直向下的大小为1 kN 的集中力,右下角及下边框距右下角0.75 m 的位置分别施加大小为1 kN、方向向下的集中力,所有组件按图中所示位置作为初始布局,组件分别编号为1~24。系统中组件及拓扑设计域的材料属性见表2。优化问题要求该系统刚度最大,以改进的混合惩罚函数方法建立优化目标,拓扑设计域为整个矩形区域,约束设计区域材料用量比的上限为0.5。

图13 简化挂架结构系统示意图Fig.13 Illustration of simplified pylon system
图13中,所有形状相同的组件尺寸均相同,涉及到5种共24个不同的组件,组件的尺寸在图14 中给出,组件的包络圆划分及其MPC连接位置如图15所示。

表2 简化挂架结构系统的材料属性Table 2 Material properties of simplified pylon system

图14 简化挂架结构系统组件尺寸Fig.14 Sizes of components in simplified pylon system

图15 简化挂架结构系统组件有限包络圆描述 Fig.15 Approximation of components in simplified pylon system by FCM
图16给出了优化过程构型迭代历史。
可见,在结构拓扑、组件布局的协同优化设计中,组件首先找到一个接近最优解的位置,随着结构构型的不断清晰,组件只在自身位置附近作微小扰动以达到最优解。组件之间的干涉可以得到有效控制,最终,所有组件之间没有干涉情况且系统目标函数收敛。
对上述算例引入质心位置约束重新计算,本例约束系统质心位置xG≥1.20 m且yG≤0.77 m。由于组件材料密度大于支撑结构材料密度,为了满足质心位置约束,组件被迫分布到靠近系统右下角点处,最终系统质心位置为(1.200,0.716) m,满足质心约束条件及组件之间的非干涉要求,系统应变能为0.066 J。不加质心与加质心的优化结果对比如图17所示。图18给出了两种情况下系统的应变能收敛曲线。
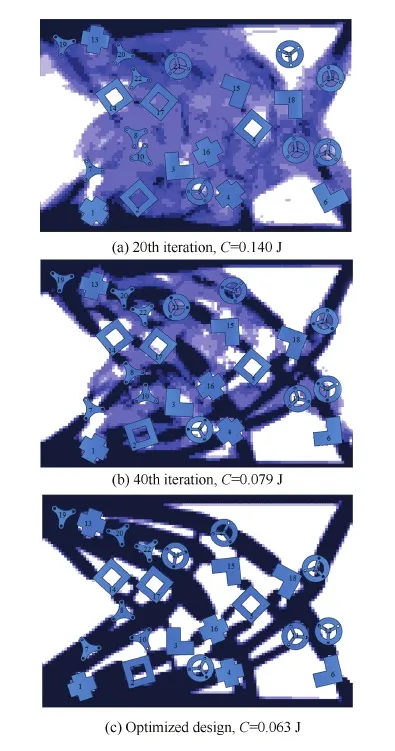
图16 简化挂架系统优化迭代历史Fig.16 Optimization design history of simplified pylon system

图17 优化结果对比Fig.17 Comparison of optimized design

图18 系统应变能收敛曲线Fig.18 Convergence history of global strain energy
3.3 结果分析与讨论
分析对比3.1节使用传统的分别约束各个干涉约束函数的组件、结构协同优化设计结果与应用本文提出的方法得到的优化结果,不难发现:本文提出的方法在处理组件之间的干涉问题上是有效可行的,对应的目标函数平稳收敛,传统的分别将各个干涉约束作为约束函数的方法,由于约束函数本身存在的非线性而不易找到可以平稳收敛的可行解。正如图9所示,传统的方法中,结构的拓扑同组件的布局不易协调,如果结构构型已经逐步清晰,一旦组件之间发生了干涉,约束函数会设法将组件分开,但此时极有可能使组件与结构之间已经形成的连接断开,导致应变能目标迅速攀升,要再次寻找到有效的可行解,仍需要多次迭代,严重的甚至找不到有效的可行解,使组件悬空。这也是图9中,传统方法优化过程中目标函数跳跃的原因。
在3.2节,由大量组件引入了大量的干涉约束函数,由于此时的干涉约束之间的非线性程度严重增加,已经使传统的方法失效,但应用本文提出的方法,在保证结构构型清晰合理的同时,可以有效避免组件之间的干涉。
4 结 论
1) 提出了多组件结构系统布局优化中处理组件干涉约束的归一化的混合惩罚函数方法,考虑了所有干涉约束函数对系统布局优化的影响,使包含组件干涉约束的优化问题变为无组件干涉约束的优化问题。
2) 本文所提方法通过数值算例有效地解决了多组件结构系统布局优化设计中的组件干涉问题,使包含大量干涉约束的多组件结构系统布局优化设计成为可能。
3) 本文提出的归一化的混合惩罚函数方法,由于其构造的函数在0点不连续,干涉约束函数在0点对组件几何设计变量的灵敏度不存在。但在实际处理过程中,组件之间的干涉约束函数基本不会在0点处停留,实际也就没有导数不存在的情况,但是为了避免这种情况的发生,本工作在干涉约束函数为0时,将其对组件几何设计变量的导数取惩罚函数的左导数0。后续工作中,实现惩罚函数在0点连续且可导是值得深入研究的问题。
[1] CHICKERMANE H, GEA H C. Design of multi-component structural systems for optimal layout topology and joint locations[J]. Engineering with Computers, 1997, 13(4): 235-243.
[2] LI Q, STEVEN G P, XIE Y M. Evolutionary structural optimization for connection topology design of multi-component systems[J]. Engineering Computations, 2001, 18(3/4): 460-479.
[3] MA Z D, KIKUCHI N, PIERRE C, et al. Multidomain topology optimization for structural and material designs[J]. Journal of Applied Mechanics, 2006, 73(4): 565-573.
[4] ZHU J H, ZHANG W H, BECHERS P. Integrated layout design of multi-component system[J]. International Journal for Numerical Methods in Engineering, 2009, 78(6): 631-651.
[5] ZHU J H, ZHANG W H. Coupled design of components layout and supporting structures using shape and topology optimization[C]//Proceedings of the Fourth China-Japan-Korea Joint Symposium on Optimization of Structural and Mechanical Systems. [S.l.]: [s.n.], 2006.
[6] ZHU J H, ZHANG W H, BECKERS P, et al. Simultaneous design of components layout and supporting structures using coupled shape and topology optimization technique[J]. Structural and Multidisciplinary Optimization, 2008, 36(1): 29-41.
[7] ZHU J H, ZHANG W H. Integrated layout design of sup-ports and structures[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199(9): 557-569.
[8] 张卫红, 郭文杰, 朱继宏. 部件级多组件结构系统的整体式拓扑布局优化[J]. 航空学报, 2015, 36(8): 2662-2669.
ZHANG W H, GUO W J, ZHU J H. Integrated layout and topology optimization design of multi-component systems with assembly units[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2662-2669 (in Chinese).
[9] MEAGHER D. Geometric modeling using octree encod-ing[J]. Computer Graphics and Image Processing, 1982, 19(2): 129-147.
[10] SAMET H, WEBBER R E. Hierarchical data structures and algorithms for computer graphics. I. Fundamentals[J]. IEEE Computer Graphics and Applications, 1988, 8(3): 48-68.
[11] MOORE A. The circle tree—A hierarchical structure for efficient storage, access and multi-scale representation of spatial data[C]//14th Annual Colloquium of the Spatial Information Research Centre. [S.l.]: [s.n.], 2002: 149-156.
[12] CAMERON S. Approximation hierarchies and S-bounds[C]//Proceedings of the first ACM Symposium on Solid Modeling Foundations and CAD/CAM Applications. New York: ACM, 1991: 129-137.
[13] 徐义春, 董方敏, 刘勇, 等. 带平衡约束矩形布局优化问题的遗传算法[J]. 模式识别与人工智能, 2010, 23(6): 794-800.
XU Y C, DONG F M, LIU Y, et al. Genetic algorithm for rectangle layout optimization with equilibrium constraints[J]. Pattern Recognition and Artificial Intelligence, 2010, 23(6): 794-800 (in Chinese).
[14] 黎自强, 田茁君, 王奕首, 等. 求解平衡约束圆形Packing问题的快速启发式并行蚁群算法[J]. 计算机研究与发展, 2012, 49(9): 1899-1909.
LI Z Q, TIAN Z J, WANG Y S, et al. A fast heuristic parallel ant colony algorithm for circles packing problem with equilibrium constraints[J]. Journal of Computer Research and Development, 2012, 49(9): 1899-1909 (in Chinese).
[15] TENG H, SUN S, LIU D, et al. Layout optimization for the objects located within a rotating vessel—A three-dimensional packing problem with behavioral constraints[J]. Computers & Operations Research, 2001, 28(6): 521-535.
[16] WANG Y S, TENG H F. Knowledge fusion design method: Satellite module layout[J]. Chinese Journal of Aeronautics, 2009, 22(1): 32-42.
[17] ZHANG W H, ZHU J H. A new finite-circle family method for optimal multi-component packing design[C]//WCCM VII. [S.l.]: [s.n.], 2006.
[18] GAO H H, ZHU J H, ZHANG W H, et al. An improved adaptive constraint aggregation for integrated layout and topology optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 289: 387-408.
[19] 单鹏. 镶嵌多个部件的结构拓扑优化设计[D]. 大连: 大连理工大学, 2008: 33-34.
SHAN P. Optimal embedding objects in the topology de-sign of structure[D]. Dalian: Dalian University of Technology, 2008: 33-34 (in Chinese).
[20] KANG Z, WANG Y. Integrated topology optimization with embedded movable holes based on combined description by material density and level sets[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 255: 1-13.
[21] COURANT R. Variational methods for the solution of problems of equilibrium and vibrations[J]. Bulletin of the American Mathematical Society, 1943, 49: 1-23.
[22] FIACCO A V, MCCORMICK G P. Extensions of SUMT for nonlinear programming: Equality constraints and extrapolation[J]. Management Science, 1966, 12(11): 816-828.
[23] CHEN Y L, HE P L, ZHANG Y H. Combining penalty function with modified chicken swarm optimization for constrained optimization[C]//First International Conference on Information Sciences, Machinery, Materials and Energy. Pairs: Atlantis Press, 2015: 1899-1907.
[24] HUANG X X, YANG X Q, TEO K L. Convergence analysis of a class of penalty methods for vector optimization problems with cone constraints[J]. Journal of Global Optimization, 2006, 36(4): 637-652.
[25] JAYSWAL A, CHOUDHURY S. Convergence of exponential penalty function method for multiobjective fractional programming problems[J]. Ain Shams Engineering Journal, 2014, 5(4): 1371-1376.
[26] YU C, TEO K L, BAI Y. An exact penalty function method for nonlinear mixed discrete programming problems[J]. Optimization Letters, 2013, 7(1): 23-38.
[27] ZHU J H, GAO H H, ZHANG W H, et al. A multi-point constraints based integrated layout and topology optimization design of multi-component systems[J]. Structural and Multidisciplinary Optimization, 2014, 51(2): 397-407.
[28] 何坚勇. 最优化方法[M]. 北京: 清华大学出版社, 2007: 349-416.
HE J Y. Optimization methods[M]. Beijing: Tsinghua University Press, 2007: 349-416 (in Chinese).
Apenaltyfunctionbasedmethodfordealingwithoverlapconstraintsinintegratedlayoutandtopologyoptimizationdesignofmulti-componentsystems
ZHUJihong*,GUOWenjie,ZHANGWeihong,HEFei
LaboratoryofEngineeringSimulation&AerospaceComputing,NorthwesternPolytechnicalUniversity,Xi’an710072,China
There are an amount of overlap constraints in the integrated layout and topology optimization design of a multi-component system containing tens of components. The integrated layout and topology optimization design of multi-component systems containing varieties of components are discussed in this paper. The finite-circle method (FCM) based penalty function is applied to deal with the overlap constraints among different components. A combined penalty function consisting of compliance and overlap constraints functions is chosen as the new objective. The gradient based optimization algorithm is implemented to maximize the stiffness of the system involving hundreds of overlap constraints, a total of tens of different components. Clear configurations of structure and non-overlapping positions of components are obtained in the simultaneous integrated layout and topology optimization deign. The optimized designs have shown the validity and efficiency of the proposed penalty function in dealing with overlap constraints in the integrated layout and topology optimization design of multi-component systems.Key words: topology optimization; multi-component system; combined penalty function; overlap constraint; finite-circle method
URL:www.cnki.net/kcms/detail/11.1929.V.20160506.1013.002.html
s:NationalNaturalScienceFoundationofChina(11432011,11172236); “111”Project(B07050);ScienceandTechnologyResearchandDevelopmentProjectsinShaanxiProvince(2014KJXX-37);theFundamentalResearchFundsfortheCentralUniversities(3102014JC02020505)
2015-12-17;退修日期2016-03-28;录用日期2016-04-29; < class="emphasis_bold">网络出版时间
时间:2016-05-061013
www.cnki.net/kcms/detail/11.1929.V.20160506.1013.002.html
国家自然科学基金 (11432011,11172236); 高等学校学科创新引智计划 (B07050); 陕西省科学技术研究发展计划项目 (2014KJXX-37); 中央高校基本科研业务费专项资金 (3102014JC02020505)
*
.Tel.:029-88493914-1222E-mailjh.zhu@nwpu.edu.cn
朱继宏, 郭文杰, 张卫红, 等. 多组件结构系统布局拓扑优化中处理组件干涉约束的惩罚函数方法J. 航空学报,2016,37(12):3721-3733.ZHUJH,GUOWJ,ZHANGWH,etal.Apenaltyfunctionbasedmethodfordealingwithoverlapconstraintsinintegratedlayoutandtopologyoptimizationdesignofmulti-componentsystemsJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3721-3733.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0137
V214.19
A
1000-6893(2016)12-3721-13
朱继宏男, 教授, 博士生导师。主要研究方向: 结构优化设计。Tel.: 029-88493914-1222E-mail: jh.zhu@nwpu.edu.cn
郭文杰男, 硕士研究生。主要研究方向: 结构拓扑优化设计。Tel.: 029-88493914-1222E-mail: wjguo@mail.nwpu.edu.cn
张卫红男, 教授, 博士生导师。主要研究方向: 多学科优化设计。Tel.: 029-88495774E-mail: zhangwh@nwpu.edu.cn
何飞男, 硕士研究生。主要研究方向: 动载作用下结构拓扑优化设计。Tel.: 029-88493914-1222E-mail: hefei@mail.nwpu.edu.cn
*Correspondingauthor.Tel.:029-88493914-1222E-mailjh.zhu@nwpu.edu.cn

