破解多元函数最值问题之策略

江苏省通州高级中学　朱丽强

破解多元函数最值问题之策略

江苏省通州高级中学朱丽强

在高考和高三模考中，多元函数最值问题可谓是一颗璀璨的“明珠”，常考常新。由于其具有“知识上的综合性、方法上的灵活性、思维上的独特性”等特点，有时让学生感到“束手无策”。其实，你只要注意平时善于总结与归纳各种解题技巧、方法与策略，在遇到具体问题时，便能综合比较、多向衡量而采取一个正确的、巧妙的、快捷的策略措施。下面本文通过对一些常见的典型例题的本质性的挖掘与分析，提出解决此类问题的一般性的策略。

评析：（1）解法一由已知条件和所求的式子，不难想到转化为“齐次型”来证明。这种问题在思维策略上具有一定的指向性，体现了对数学基本方法的掌握。

（2）解法二的关键点在于：变化换元，创设条件改变易寻找关系的变量。这种解题的策略往往会寻找到问题的衔接点，架设起解题的绿色通道，从而能达到出奇制胜的效果。这类题往往能很好地反映学生的思维层次与能力水平。

（3）本题也可采用“三角换元”求解。

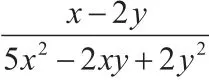
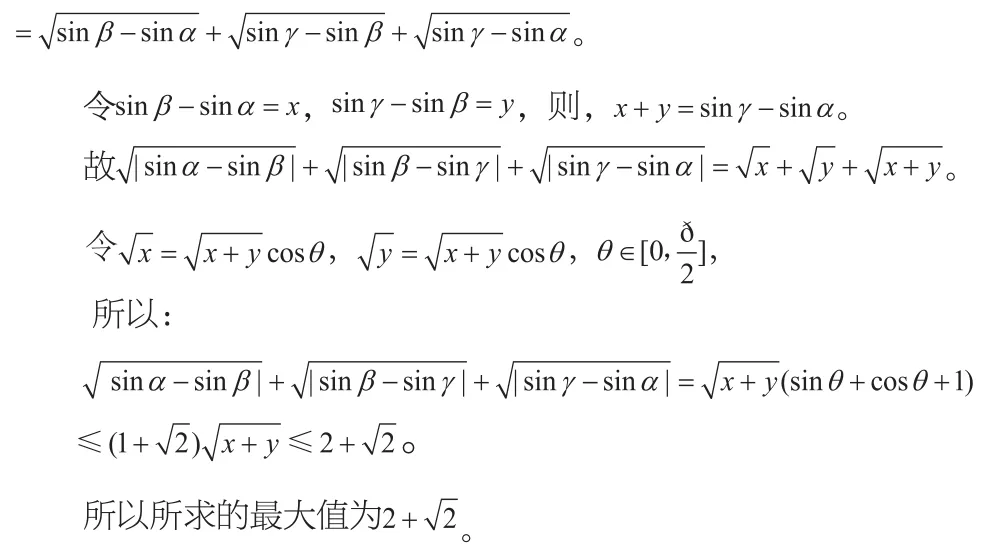
评析：（1）解法一的解题关键点在于：利用基本不等式。它是解决最值问题的立足基本，是占有突出地位的常用方法。在解决有关多元函数最值问题时，我们未必让学生总是片面追求解题的特殊技巧而忽视了数学中的通性通法，这样会使数学能力成为毫无根基的“空中楼阁”。

（2）解法二的解题技巧在于：三角换元。从而转化为三角函数的最值问题。这种转化的解法，需要学生具备一定的数学素养和解题机智，也凸显了换元转化的神奇功效。

例3：设实数a，b，c满足a2+b2≤c≤1，求a+b+c的最小值_______。

评析：（1）解法一的关键是通过消元转化为二次函数的最值问题求解。

（2）解法二的关键点在于：“利用基本不等式”的技巧，这种技巧产生在充分的观察、思考与研究之后。在求解数学的问题时，首先就应该从宏观上把握问题，透过信息的表象，能抓住问题的本质，再从微观上明确解题的方向。

（3）解法三通过三角换元巧妙地将一些重要数学思想方法寓于问题的解决之中，曲径通幽，耐人寻味。

以上解决多元函数最值问题的思路与方法告诉我们：见多识广，可以增强领悟能力，博采众长，才能减少盲目性。解题中的灵感突现，源自平时的日积月累，只有多钻研，多探索，做题时便能随机应变或独辟蹊径，以致迎刃而解。