基于禁忌搜索的车联网蒙特卡洛定位算法
孙友伟,王辰寰,张 晶
(西安邮电大学 通信与信息工程学院,西安 710121)
基于禁忌搜索的车联网蒙特卡洛定位算法
孙友伟,王辰寰,张 晶
(西安邮电大学 通信与信息工程学院,西安 710121)
在蒙特卡洛定位算法中引入禁忌搜索算法以提高车联网中快速定位的性能;自组织车联网高速移动的车辆和快速变化的网络拓扑结构,使用传统的蒙特卡洛定位算法,不能迅速地收敛位置信息;在滤波阶段引入禁忌搜索算法对传统蒙特卡洛定位算法进行改进, 优化滤波排除可能性较小的位置点,获得近似最优估计位置采样集;仿真结果表明,改进后的算法在样本采集数、计算时间、定位精度等方面有了显著提升,改进后的算法能更好地解决车联网的定位问题。
蒙特卡洛定位;禁忌搜索算法;车联网;距离无关;定位
0 引言
物联网现今得到了长足的发展,诸如电力线通信、车联网等新兴领域成为物联网研究的热点[1],基于车联网的定位也成为业内急需解决的问题。传统的移动节点定位算法基本归纳为两类,一类是基于距离的定位算法,比如利用信号强度、到达时间、方位角度等确切物理值进行定位;另一类是与距离无关定位算法,通过连通网络间传送的消息进行定位[2]。一般而言基于距离的定位算法精确度较高,但其缺点也很显著,比如对硬件要求高、易受周围环境影响等;与距离无关定位算法通常来讲其定位精度不高。但其优点也很显著,比如不需时间同步、对硬件要求不高、节省能耗等[3]。传统的定位算法大多面向静态网络,不能有效解决车联网中汽车节点随时动态变化的问题,这成为近来车联网定位面临的一个主要难点。
1 提出问题
我们设计的车联网是基于自组织网络并且网络中移动节点高速运动,网络拓扑结构高度动态变化[4],传统定位方法已经不适用。根据车联网这一结构特点,本文提出一种改进型的蒙特卡洛(MCL)定位算法。Monte Carlo方法由美国科学家冯.诺依曼等人首先提出,后来广泛应用于经济、物理、生物医学领域,主要用于统计模型的建立。Monte Carlo方法首次用于定位领域是Sebastin Thrun等人通过蒙特卡洛采样确定移动机器人所处位置的概率[5]。MCL定位算法根据节点移动性构建数学模型[6],在贝叶斯滤波位置估计的基础上,利用若干个带有权重的采样点来计算移动节点在某一位置出现的概率,最终实现节点定位[7]。但是我们在仿真MCL定位算法的过程中发现,传统的MCL算法计算量大,位置估测样本较大,滤波过程耗时较长,且定位精度不高。因此我们在传统MCL算法滤波阶段引入禁忌搜索算法,经过一系列实验证明,改进后的算法与传统MCL算法相比,改进后的算法能够很好地适应车联网节点动态变化,并在样本集数量、计算时间、定位精度等几项参数指标方面均有显著提升。禁忌搜索算法(Tabu Search,TS)是一种全局优化算法。禁忌搜索算法广泛应用于路由优化、函数优化等方面[8]。禁忌搜索算法在滤波优化定位方面能够很好地契合车联网中高速移动节点快速定位的需求。
本文提出的TS-MCL算法属于与距离无关定位算法,该算法不仅能够满足与距离无关定位算法的各项优点,而且通过对传统MCL定位算法的改进,TS-MCL能达到较高的定位精度。
2 网络模型描述
在城市智能交通的车联网模型中,城市按照一定面积划定一个区域,区域内设若干固定路基信息点,这些信息点与其覆盖范围内的车辆进行双向通信,用于采集车辆实时信息以及向车辆传送交通控制中心的实时播报。设每一个信息点为锚节点,锚节点为静止状态,锚节点每隔一定时间发出包含锚节点自身位置信息的轮询信号,则以锚节点为圆心、锚节点所发送信号的最大传输距离为半径的圆内的所有移动节点均能接收到轮询信号。模型不考虑环境对信号的干扰等问题,并确保锚节点发出的轮询信号可以被不大于νmax速度运动的移动节点随时接收。
车联网中移动节点定位的相关空间变量定义如表1所示。
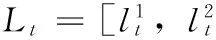
(1)
状态更新方程为:
(2)
将式(1)代入式(2),因为p(ot|o1:t-1)是归一化常量,所以看作已知数,故对于p(ot|lt)、p(lt|o1:t-1)、p(lt|o1:t)三者来说,只需要得任意两个,即可得第3个[9]。
3 TS-MCL算法描述
3.1 位置初始化
3.1.1 初始化
移动节点在定位以前并不知晓关于其自身所在N个位置的先验位置信息,故需要对其进行初始化操作(N表示算法执行过程中所要维持的采样数)。
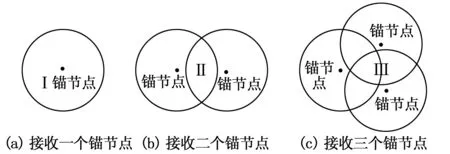
图1 移动节点估测范围
估测范围的确定如图1所示,当移动节点接收到一个锚节点的位置信息时,其估测范围为Ⅰ(图1(a)),锚节点为中心的信号传输最大距离为半径的圆形区域。当移动节点接收到两个锚节点的位置信息时,其估测范围为Ⅱ(图1(b)),即两个锚节点交叉覆盖范围。当移动节点接收到3个锚节点的位置信息时,其估测范围为Ⅲ(图1(c)),即3个锚节点交叉覆盖范围。同理,可得移动节点接收到更多锚节点位置信息时的估测范围。
L0=[移动节点所在区域内随机确立的 N个可能位置]
3.1.2 循环计算
根据Lt-1以及Ot计算Lt,三者分别代表上一时间段内移动节点的可能位置序列、新的观测值、移动节点新的可能位置。
初始位置确定后,每间隔一定时间通过移动节点的运动情况和新的观测信息对移动节点的位置序列进行位置更新。
3.2 位置预测

(3)
将式(3)的计算结果代入式(1)中,可计算出预测方程中的p(lt|o1:t-1)值。
3.3 TS寻优滤波
在滤波过程中采用禁忌搜索策略(TS)通过优化滤波排除可能性较小的位置点,获得近似最优估计位置采样集[11]。与传统MCL算法滤波过程相比较,禁忌搜索算法通过较少的迭代次数和暂时锁定局部极值引导搜索向其他路径延伸,在节约时间和提高准确度上有着明显的优势[12]。位置采样集中的元素依靠领域函数产生领域元素集,通过建立禁忌表避免陷入局部最优,使得采样集中的元素向更多路劲搜索,并利用特赦准侧释放性能良好的被禁元素,最终实现全局优化。
在t时刻采样集Lt利用TS寻优滤波方法优化滤波过程如下:
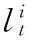
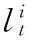
(4)
式(4)中,N(0,1)是均值为0,方差为1的正态随机数。若新产生的领域元素集中的元素与禁忌表中有重复,则重新产生领域元素集,避免迂回搜索。上式表明,权值较大的元素领域范围小,权值较小的元素领域范围大,产生的元素集更合理有效;
5)判断该元素是否满足终止条件,若满足,进行下一步,否则返回步骤2)。
终止条件:
(5)
式(5)中,U(0,1)表示[0,1]均匀分布的随机数;
算法最后得出最优或近似最优值即为要计算的当前t时刻的p(lt|ot)值。
综上所述,TS滤波算法通过建立禁忌表实现对局部极值一定时间的锁定,不会陷入局部极值,从而实现向其他路径搜索,最终依靠特赦准则释放优良元素,通过迭代实现步步接近最优值,从而实现全局最优化。这样的搜索过程既不会遗漏优化值,又能提高搜索效率。
算法流程如图2所示。
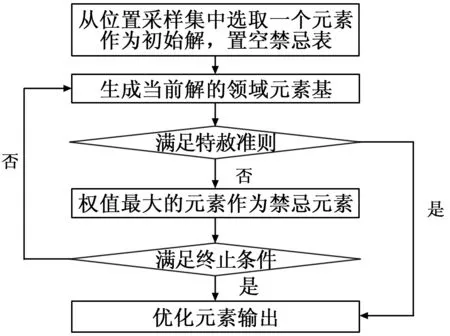
图2 禁忌搜索寻优滤波流程图
3.4 重要性采样及定位
重要性采样是将节点位置采样值通过标准化重要性采样函数π获得,并调整这些相互独立的节点采样值的权重值,利用权重值对节点可能位置作出后验概率分布估计。具体运用了如下递归式的重要性函数。
(6)
(7)
(8)
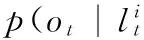
(9)
(10)
4 仿真性能分析
为了评估TS-MCL算法性能,我们对算法收敛性、样本集数量、计算时间、定位精度进行仿真测评。这里我们采用均方根误差(RMSE)来衡量定位算法的误差。
(11)
式(11)中,x、y代表被测量点的横、纵坐标的真实值,x′、y′代表被测量点的横、纵坐标的测量值。
仿真环境设置锚节点通信半径为1 000 m,区域内有40个移动节点,移动节点移动速度不大于50 m/s,移动节点能接收到两个锚节点的位置信息。则TS-MCL算法的收敛状况如图3所示。
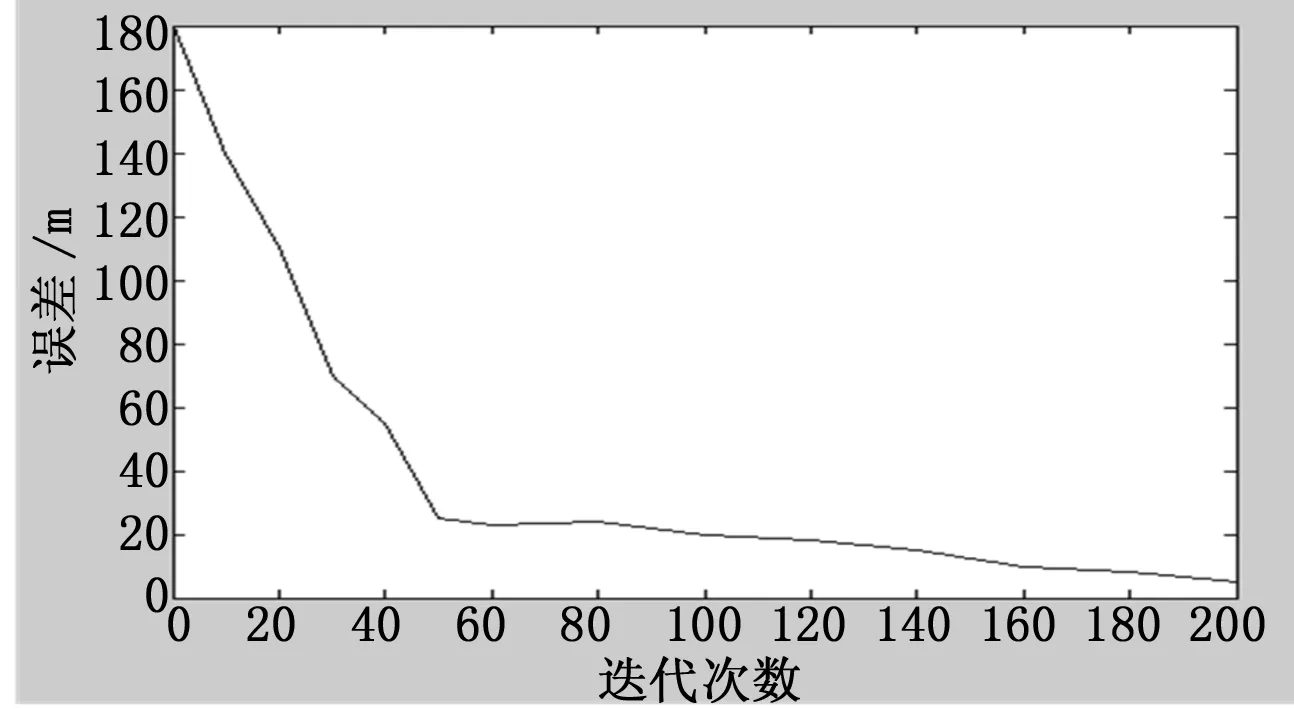
图3 算法收敛性证明
其中纵坐标代表TS-MCL算法定位误差,横坐标代表TS-MCL算法的迭代次数,由仿真图可知,在0~50步迭代过程中算法误差下降较快,100步之后,算法误差下降趋于平稳,误差测量值约为5 m,算法整体趋于收敛。
仿真环境参数设置仍如上所述,图4描述了TS-MCL算法在不同样本数量情况下,定位误差的变化情况。
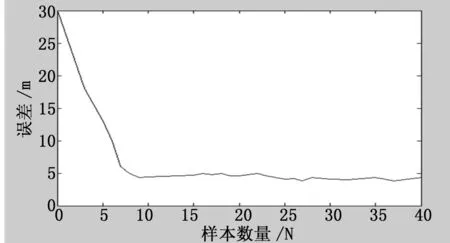
图4 定位误差受样本数量的影响
图中横坐标代表样本数量,纵坐标代表均方根误差。由图可知,TS-MCL算法在1~8个样本数时定位误差急剧下降,之后误差趋于平稳,得出采样样本数量占总体样本数的20%时,算法即可达到一定误差范围内的定位,与传统MCL算法比较,采样样本数量大幅减少。
图5描述了传统MCL算法与TS-MCL算法在不同迭代次数的情况下定位时间的对比。
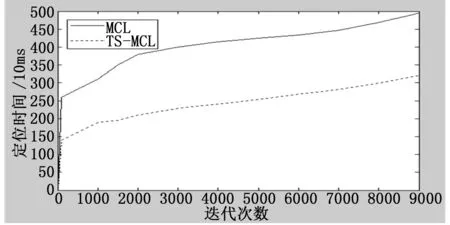
图5 TS-MCL算法与MCL算法定位时间对比
其中横坐标为迭代次数,纵坐标代表定位时间。由图可知,TS-MCL算法在相同迭代次数下,相较于传统MCL算法定位时间减少30%以上,这是因为TS-MCL算法在寻优滤波和重采样定位阶段计算量大大减小,导致算法整体计算时间缩短。
图6描述了在锚节点通信半径不同的情形下传统MCL算法与TS-MCL算法两种定位算法定位误差的对比。仿真条件设定移动节点能够接受到两个锚节点的位置信息。
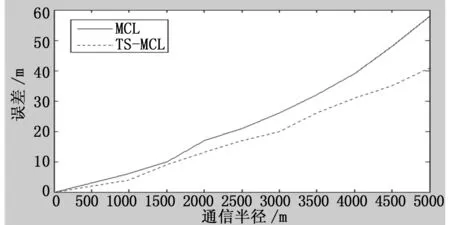
图6 TS-MCL算法与MCL算法定位误差比较
图6中横坐标代表锚节点的通信半径,纵坐标代表均方根误差。从图中可以看出,由于锚节点通信半径增大,定位精度都会下降,但同等通信半径条件下TS-MCL算法定位精度较传统MCL算法提高了10%以上。
5 总结
本文通过在滤波阶段引入禁忌搜索算法对传统MCL算法进行改进,仿真结果表明改进后的算法与传统MCL算法相比较在样本采集数、计算时间、定位精度等方面有了显著提升,改进后的算法能更好地解决车联网的定位问题。
[1] 孙友伟,温双涛.基于电力线通信的新型物联网架构[J].西安邮电大学学报,2014,19(3):43-48.
[2] Sheu J P,Hu W K,Lin J C.Distributed localization scheme for mobile sensor networks[J].IEEE Transactions on Mobile Computing,2010,9(4):510-512.
[3] 董振中.无线传感器网络无需测距的高效定位算法的研究[D].合肥:中国科学技术大学,2010:23-26.
[4] 孙友伟.现代通信新技术新业务[M].北京:北京邮电大学出版社,2004.
[5] 梅 举,陈 涤,辛 玲.基于蒙特卡洛方法的移动传感网节点定位优化算法[J].传感技术学报,2013,26(05):689-694.
[6] 孔凡天.无线传感器网络节点定位与数据融合技术研究及实现[D].武汉:华中科技大学, 2006 .
[7] 朱海平,于红丞,钟小勇,等.动态无线传感器网络的改进蒙特卡洛定位算法[J].传感技术学报,2012,25(9):1284-1288.
[8] 张玉芳,薛青松,熊忠阳.基于禁忌搜索的动态粒子群算法[J].计算机工程与应用,2008,44(24):56-58.
[9] 刘文文,宋国治,孙学梅,等.基于捕食搜索策略MCL算法的蜂窝网移动终端定位问题的研究[J].小型微型计算机系统,2015,36(1):54-59.
[10] 乔 峰,王思民.基于MCL算法的无线传感网络节点定位技术[J].山西电子技术,2009(03):63-64.
[11] 王 龙,夏厚培.禁忌搜索粒子滤波算法在目标跟踪中的应用[J].科学技术与工程,2013,13(06):1630-1634.
[12] Boer S Y,Driessen J N. Interacting multiple model particle filter[J].IEE Proc. of RadarSonar Navigation,2003,150(5):334-349.
A Monte Carlo Localization Algorithm Based on Tabu Search in Car Networking
Sun Youwei, Wang Chenghuan,Zhang Jing
(School of Communication and Information Engineering, Xi′an University of Posts and Telecommunications, Xi′an 710121, China)
Tabu search algorithm is introduced in Monte Carlo localization algorithm to improve the car networking quickly locate performance.Ad-hoc car networking vehicles moving at high speed and network topology rapidly changing,the use of traditional Monte Carlo localization algorithm,can not quickly converge location information.Tabu search algorithm is introduced in the filtering stage of the traditional Monte Carlo localization algorithm to filter optimization and exclude the small possibility points, to obtain approximate optimal sample set of the estimated position.Simulation results show that the improved algorithm in the number of sample collection,computation time,positioning precision,has been significantly improved,the improved algorithm can better solve the positioning of car networking.
MCL;tabu search algorithm;car networking;independent of distance;positioning
2016-01-05;
2016-01-20。
孙友伟(1956-),男,陕西西安人,教授,硕士研究生导师,主要从事下一代通信网方向的研究。
1671-4598(2016)06-0240-04
10.16526/j.cnki.11-4762/tp.2016.06.066
TN913.6
A

