基于状态反馈的LCL型逆变器解耦控制策略

屈克庆 李文旗 叶天凯 赵晋斌 李 芬



基于状态反馈的LCL型逆变器解耦控制策略

屈克庆 李文旗 叶天凯 赵晋斌 李 芬

（上海电力学院电气工程学院 上海 200090）

为实现带LCL滤波器的三相电压源型并网逆变器（VSI）的无静差控制，通常采用abc/dq变换将静止坐标系转换为同步坐标系，但这种变换存在dq分量间的耦合问题。因此提出了一种基于双电感电流和电容电压反馈的三闭环解耦控制策略，该策略采用状态反馈实现了多输入多输出（MIMO）线性时不变系统动态解耦，不仅有效解决了dq分量间的耦合问题，而且在保证较高的入网电流质量的条件下改善了系统动态性能。仿真和实验结果均验证了该控制策略的可行性和有效性。

同步坐标系 LCL滤波器 并网逆变器 状态反馈 解耦控制

0 引言

能源危机、温室效应等问题的出现，促进了新能源发电技术的迅速发展，新能源发电技术因此成为研究热点[1,2]。随着新能源比重的不断增加，电网公司对新能源并网发电系统在各方面都提出了更加严格的标准，如要求并网系统具备较高的入网电流质量、准确的功率调节能力等[3,4]。因此，改善并网逆变器入网电流电能质量以及准确控制其功率输出具有重要意义。

电压源型并网逆变器（Voltage Source Inverter, VSI）通常采用脉宽调制（Pulse Width Modulation, PWM）技术[5]，其输出电流中含有高次谐波，无法满足并网要求。因此，VSI输出与电网之间需要接入滤波器，来提高并网逆变器入网电流电能质量。常用L型和LCL型两种类型滤波器，LCL型滤波器与L型滤波器相比有更理想的高频滤波效果，且体积和损耗均小于同等滤波效果的L型滤波器。然而，LCL型滤波器为高阶系统，增加了控制器的设计复杂度[6,7]。如何通过改进控制策略提高LCL型并网逆变器性能受到了广泛关注[8-10]。

根据参考坐标系的不同，VSI控制器可分为基于静止自然坐标系[11,12]和基于旋转两相同步坐标 系[13-15]两类。在静止自然坐标下，比例谐振（Proportional Resonance, PR）控制器能够直接对交流信号进行跟踪，避免了坐标变换所引起的耦合问题，然而PR控制器存在数字化实现困难及难以实现无静差跟踪等问题。因此，大多数应用场合选择基于同步坐标系的控制策略。在同步坐标系下，三相交流信号经过abc/dq坐标变换为两相直流信号。但是变换得到的dq分量间存在耦合，该问题在LCL滤波器情况下变得尤为突出，严重影响控制系统的动态性能[16,17]。

针对耦合问题，虽然将耦合项当作外部干扰项直接忽略的传统双闭环方案可以在很大程度上降低控制器的设计难度，实现dq分量之间的独立控 制[18]，然而，直接忽略耦合项必然引起建模失真，导致输出电流质量降低。文献[19]通过分析系统传递函数关系，在控制策略中引入耦合补偿项。与直接忽略耦合项相比，该方案虽能提高了模型准确度，能够保证较高的输出电流质量，但却无法完全消除dq分量间耦合影响。

为此，本文提出了一种基于状态反馈的双电感电流和电容电压反馈的三闭环解耦控制策略。首先阐述LCL型输出滤波器存在耦合的原因，分析采用状态反馈实现多输入多输出（Multiple Input Multiple Output, MIMO）系统动态解耦的基本原理；其次设计解耦控制器并整定控制器参数；最后，通过与传统双闭环方案、补偿耦合项的双闭环方案的仿真和实验对比，验证本文所提出控制策略的可行性与优越性。

1 原理分析

图1为带LCL滤波器的并网VSI结构，图1中dc和1分别表示逆变器直流侧电压与输出交流电压，u表示电容电压，表示电网电压，1、2、i分别表示流过电感1、2及电容的电流。

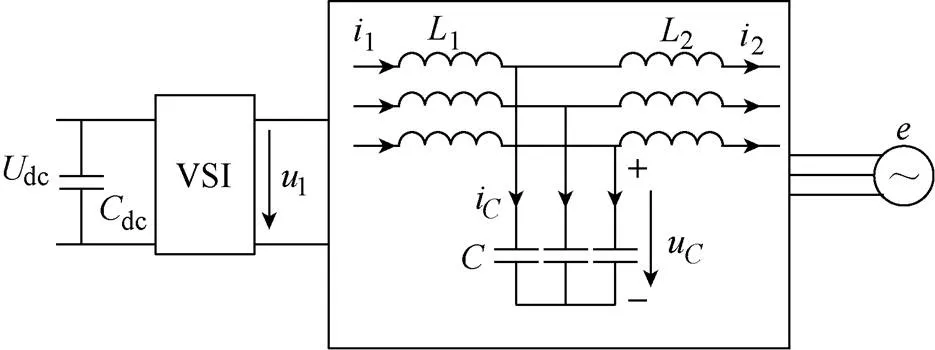
图1 带LCL滤波器的并网VSI结构

以电感1为例，分析所提出方案实现解耦的原理。在同步旋转坐标系下，对电感1有

式中，为电网电压角频率，可通过锁相环技术获取[20,21]。

由式（1）可知，1出现dq分量耦合项分别为11q和11d。状态反馈实现解耦的原理如下。

将式（1）写成状态空间形式为

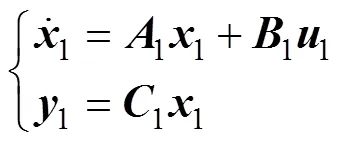
其中

该MIMO线性时不变系统传递函数矩阵为

式（3）所示的传递函数矩阵为非对角矩阵，表明该MIMO系统存在耦合。可引入状态反馈实现对角化，进而实现动态解耦。引入状态反馈1后，可得到系统传递函数矩阵为

式中，表示2阶单位矩阵。

为保证解耦后系统传递函数矩阵为对角阵，得

解耦后的传递函数矩阵为

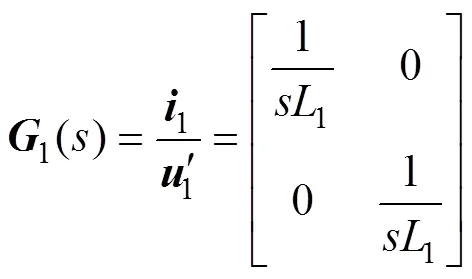
其中

对电容及电感2采用同样的方案进行解耦后，可以得到解耦后模型结构如图2所示。

图2 解耦后模型结构

根据以上分析可知，所提方案实质上是通过状态反馈引入与原耦合项大小相等的补偿项来抵消原耦合项，进而达到解耦目的。故所提出方案的解耦性能由状态反馈引入的补偿项是否与原耦合项相等直接决定。然而，计算补偿项所采用的滤波器参数值与实际值之间必然存在一些偏差，有必要分析这种差异对解耦性能的影响。以电感1为例，设定其实际值为1，计算时所采用值为1，于是状态反馈矩阵变为

耦合作用的大小可以用耦合项之间传递函数的模值来衡量。将式（7）代入式（4），得到耦合项间传递函数的模的表达式为

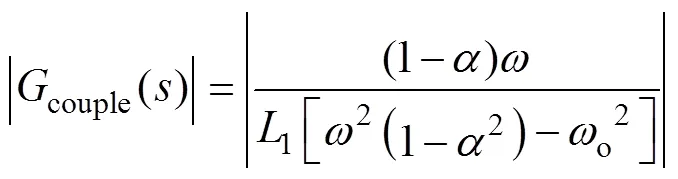
选定角频率o等于电网电压角频率时，得到耦合项间传递函数的模与的关系如图3所示，图3中纵轴值用标幺值表示，其基准值为=0.5时所对应值。图3中，所提出方案的解耦性能与的值直接相关，越接近1，解耦性能越好，对电容及电感2有相同的结论。

图3 与a 的关系

必须指出的是，实际应用中滤波电感电容与其标称值间必然存在误差，但误差值一般不会太大，即的值很接近1。因此，所提出的方案在实际应用中即使无法完全消除耦合影响，也能够很大程度上减小这种耦合影响。在实际应用中也可以通过实时调整计算值以获得满意的解耦性能。

2 控制器设计

以d轴为例，为实现本文所述的状态反馈解耦方法，需对电感电流1d、2d及电容电压ud均进行反馈，故采用图4所示带LCL滤波器的并网VSI解耦控制框图。图4中，2d表示入网电流d轴分量给定值，P1、I、P2和P3分别表示各控制器参数。入网电流2d外环采用PI控制器，以实现状态反馈解耦方法及对给定值的无静差跟踪。以电容电压ud及机侧电感电流1d为中环和内环，采用P控制器，以实现状态反馈解耦方法。另外，LCL滤波器存在由于阻尼不足而引起的谐振问题。现有研究指出，可以采用电容电流id或机侧电感电流1d反馈来实现有源阻尼。因此，所提方案中机侧电感电流1d反馈有增加阻尼、抑制谐振的作用。

由图4得到该解耦控制系统入网电流2d与其给定值2d之间的开环传递函数为

图4 带LCL滤波器的并网VSI解耦控制框图

其中

式中，PWM为逆变器等效环节，忽略开关死区时间，PWM=1。

系统闭环传递函数为

运用劳斯稳定判据可得系统稳定的条件为

在设计控制器参数时，只要满足式（11）所示不等式组，即可保证系统的稳定性。

将式（9）变换为典型环节串联的形式，得到

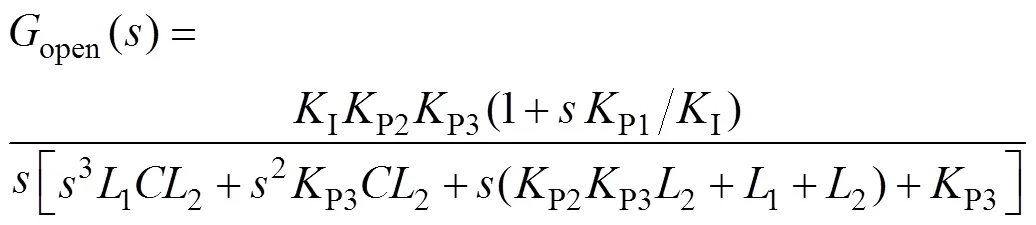
利用频域理论分析各参数与系统稳定性间的关系。在低频段，可忽略312项，系统开环传递函数可近似等效为式（13）。在低频段，该系统包含一个比例环节、一个一阶积分环节、一个微分环节及一个振荡环节。

在高频段，可忽略P3项，系统开环传递函数可近似等效为式（14）。在高频段，该系统由一个比例环节、一个二阶积分环节、一个微分环节及一个振荡环节串联组成。

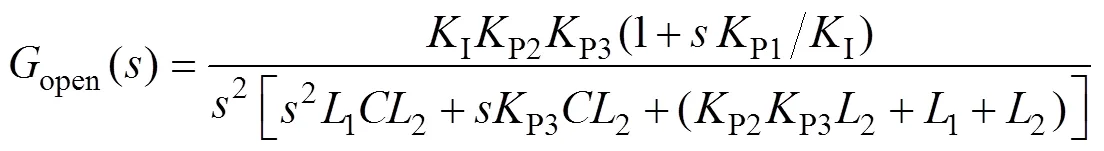
选择一阶微分环节转折频率1=I/P1进入高频段，同时为了保证系统具有足够的稳定裕度，设定幅频特性曲线以-20dB/dec的斜率穿过0dB线。根据典型系统幅频特性可画出系统近似开环幅频特性如图5所示。其中0表示低频段与高频段的分界频率，2表示振荡环节转折频率，c表示开环系统截止频率，3表示二阶微分环节与比例环节作用时的截止频率，即

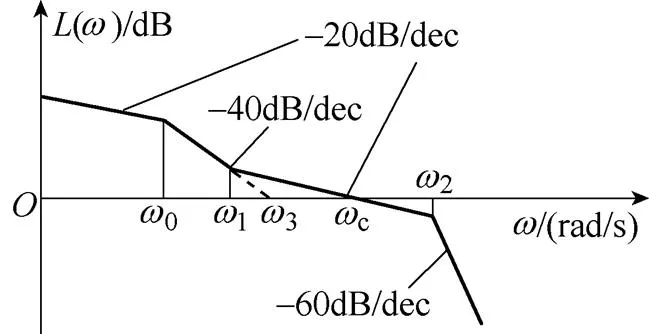
图5 系统近似开环幅频特性

选择滤波器参数：1=2mH、=20mF、2=1mH，设定振荡环节阻尼系数=0.707，由

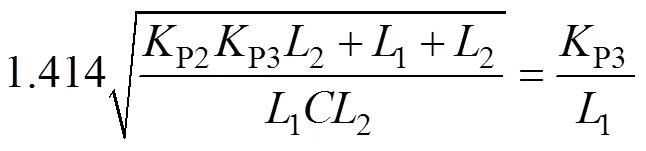
系统带宽=2/1=10。同时，由图5可知1＜3＜c，可选择3=21，得到

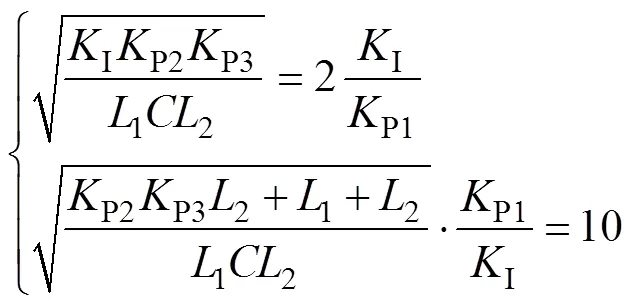
于是每选取一个P3的值即可得到一组控制参数。不同P3值对应的系统开环伯德图如图6所示，P3的值分别为50、100和200时，系统的幅值裕度分别为9dB、14dB和19.4dB，相位裕度分别为48.7°、47.8°和47.7°。根据系统稳定裕度要求可知，以上P3值均能保证系统拥有良好的稳定性。本文选择P3=100，计算得到P1=15.045，P2=0.47，I= 53 190，满足式（11）所给出的稳定条件，验证了以上参数设计的正确性。

图6 不同KP3所对应的系统开环伯德图

实际控制系统采用数字控制，选定采样频率为10kHz，并考虑数字离散化过程中的延时时间为半个采样周期，作出闭环系统零极点分布如图7所示。由图7可知，由于延时作用的影响，闭环系统增加了一个极点和一个零点。其中，有一个零点位于单位圆外，其余5个闭环极点和3个闭环零点（除去坐标原点）均位于单位圆内，故闭环系统是稳定的。

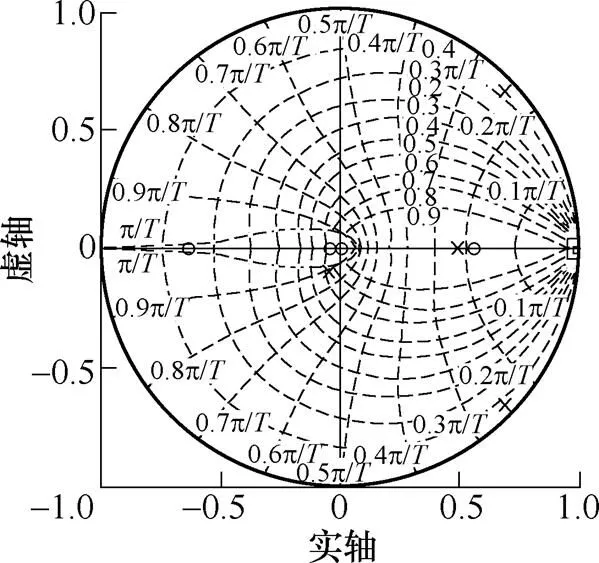
图7 闭环系统零极点分布

在元器件设计初期，测量仪器误差等因素可能导致实际参数与理论参数之间存在一定的偏差。另外，在实际应用中，由于温度的变化、元器件自身损耗以及电磁干扰等因素的影响，滤波器中元器件的参数也会发生变化。由以上分析可知，滤波器参数值与系统稳定性有直接关系。因此，有必要分析滤波器参数变化对系统稳定性的影响。

按照分析所得控制器参数，分别作滤波器参数1、、2变化时系统的开环伯德图，如图8所示。图8中，虚线箭头方向为参数值增大方向。电感1参数值在1～3mH之间按50%变化时，开环系统的幅值裕度分别为19.7dB、16.5dB、14.1dB、12.4dB与10.8dB，相位裕度分别为48°、47.9°、47.9°、47.8°与47.6°。电容参数值在10～30mF之间按50%变化时，开环系统的幅值裕度分别为16.5dB、15dB、13.7dB、12.4dB与11.1dB，相位裕度分别为65.6°、59.4°、51.3°、43.2°与33.3°。电感2参数值在0.5～1.5mH之间按50%变化时，开环系统的幅值裕度分别为8.54dB、11.7dB、14dB、15.9dB与17.3dB，相位裕度分别为39.9°、46.2°、47.2°、46.7°与44.8°。由此可知，所设计的控制系统对滤波器参数的变化具备一定的鲁棒性。

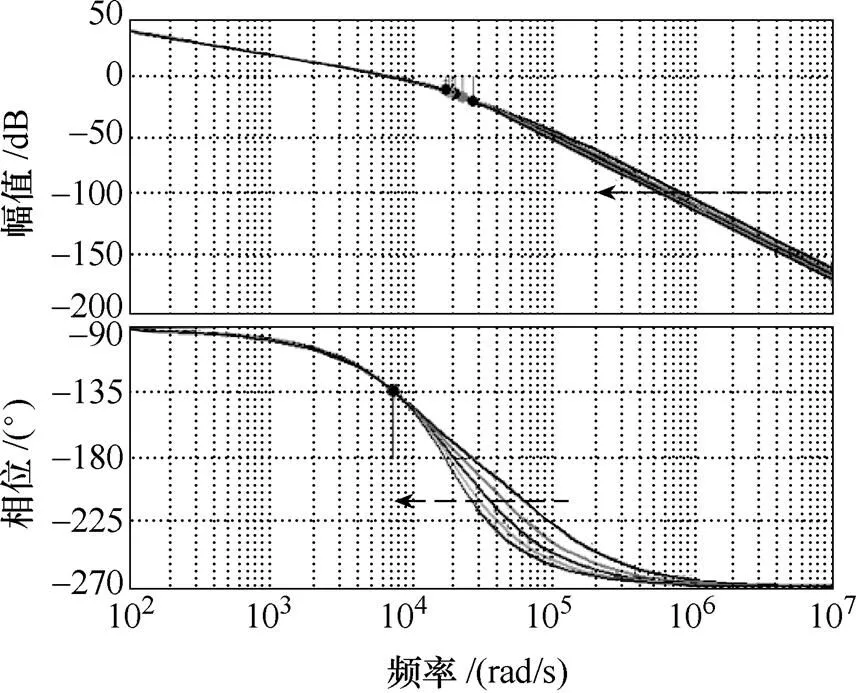
（a）1变化±50%

（b）变化±50%

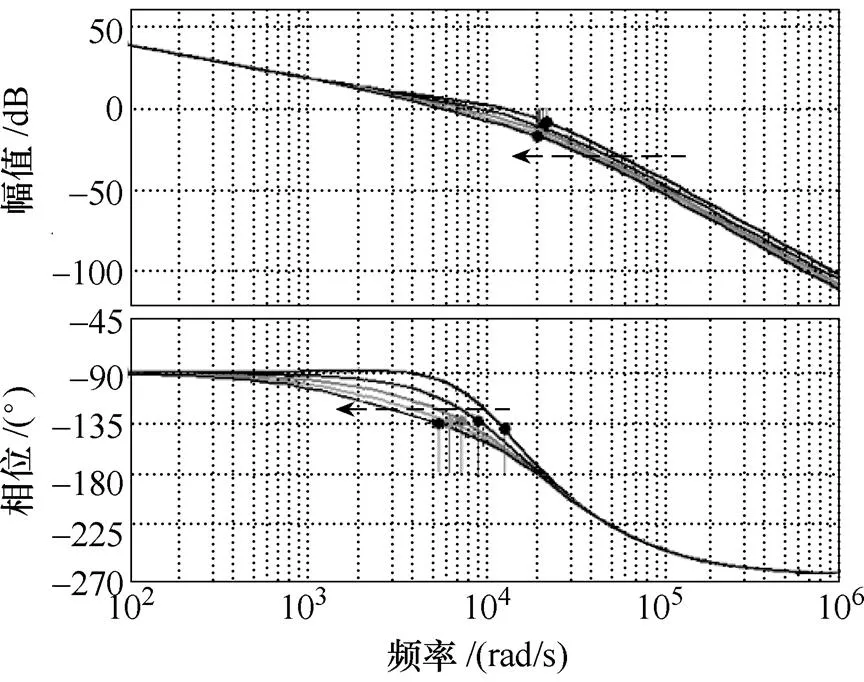
（c）2变化±50%

图8 滤波器参数变化时系统开环伯德图

Fig.8 Bode plots of the open-loop system when the parameters of filter change

3 仿真与实验

3.1 仿真

为说明所提出解耦控制方案的有效性，对所提出方案（方案1）、传统直接忽略耦合项的双闭环控制方案（方案2）及补偿耦合项的双闭环控制方案（方案3）在Matlab/Simulink平台进行了仿真，方案1仿真参数见表1。

表1 仿真参数

Tab.1 Parameters of simulation

设定仿真总时间为0.2s，当0.1s时给定有功功率由额定功率7.6kW阶跃变为3.8kW。仿真情况下，三种控制策略的输出三相入网电流及其dq分量波形如图9～图11所示。由仿真结果得到以下结论。

（1）由各个方案的THD分析结果可知，无论输出功率多大，相对方案2，方案1与方案3均有更高的入网电流质量。

（2）对比三种方案输出电流dq分量波形可知，在有功功率指令阶跃变化时，方案3输出电流d、q分量均出现明显抖动，方案1和方案2输出电流没有出现明显变化。表明方案1和方案2均具备消除这种耦合影响的作用，方案3无法消除功率变化时有功与无功间的耦合影响。

（3）对比三种方案输出电流波形可知，与方案3相比，由于方案1和方案2消除了有功分量与无功分量间的耦合影响，因而在功率变化时有更好的动态性能。

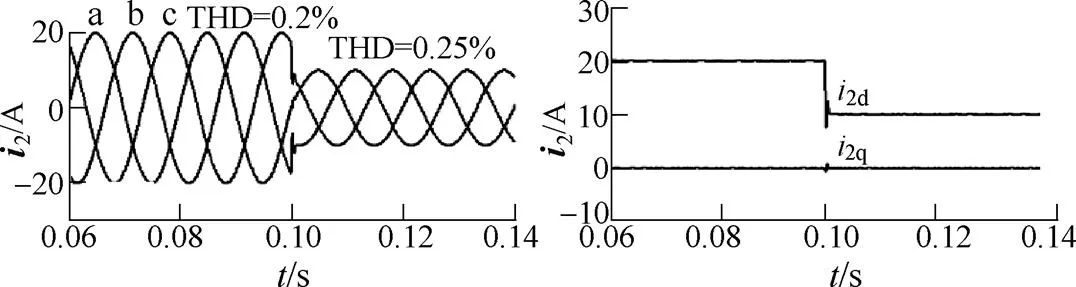
图9 方案1入网电流仿真波形

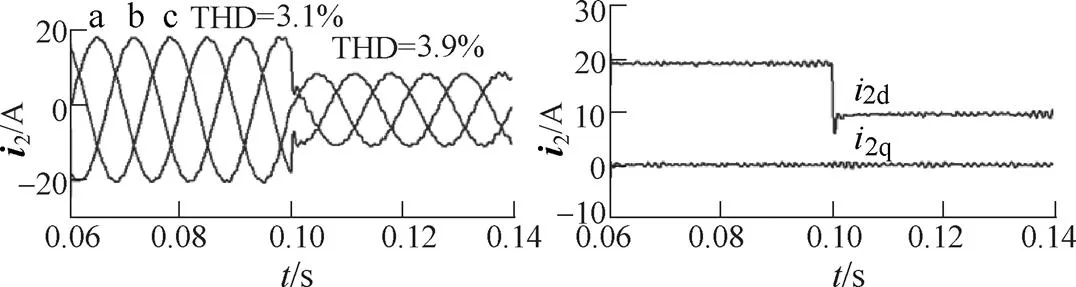
图10 方案2入网电流仿真波形

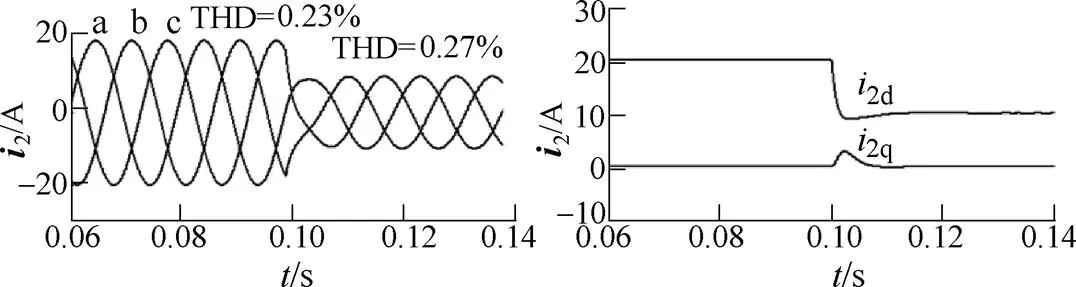
图11 方案3入网电流仿真波形

3.2 实验

基于上述理论分析与仿真结果，在一台额定功率为7.6kW的样机上对上述三种方案进行了实验分析，实验系统如图12所示。采用可编程PV直流电源作为直流侧电源，功率分析仪1用于网测量分析，功率分析仪2用于机侧量分析，TMS320F28334DSP作为主控制芯片。

图12 实验系统

如上分析，为了获得满意的解耦性能，DSP计算所采用的滤波器参数与其实际参数应当尽量保持一致。不同输出功率时，由LCR819智能LCR测量仪测得LCL滤波器参数见表2，测量精度为0.05%。实验中的其他参数与仿真情况一致。

运行过程中，有功指令信号发生阶跃变化，由7.6kW阶跃跳变为3.9kW。a相电网电压与方案1入网电流的波形如图13所示。三种方案的入网电流dq分量如图14～图16所示。

表2 LCL滤波器实测值

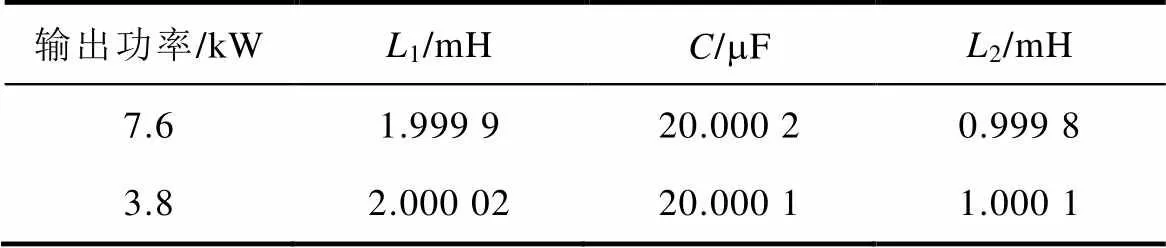
Tab.2 Actual values of LCL filter

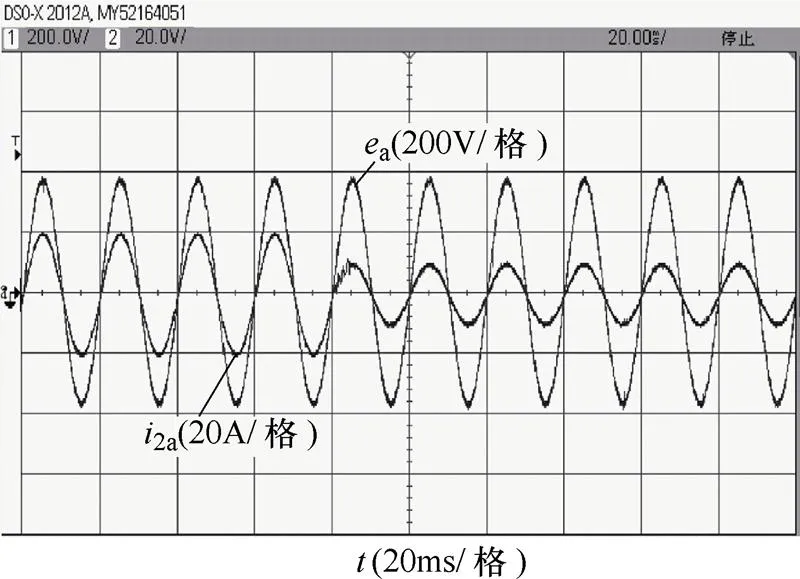
图13 a相电网电压与入网电流波形

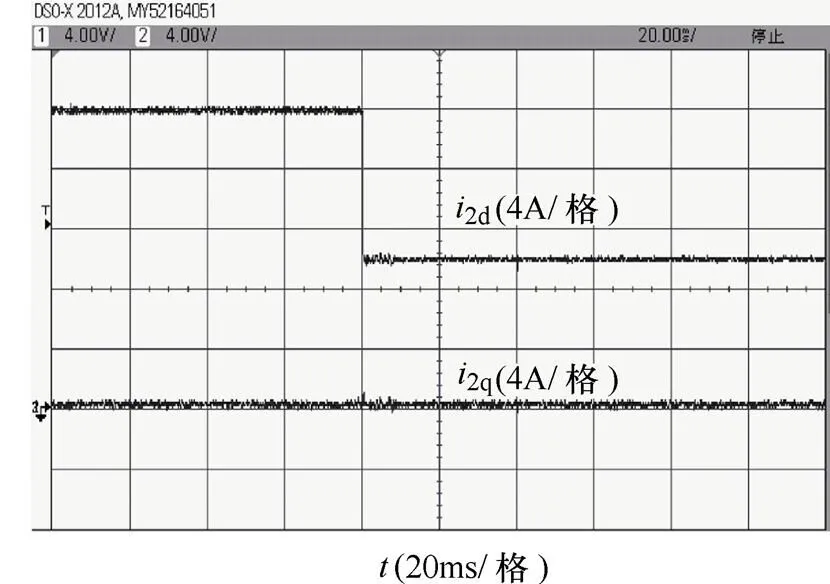
图14 方案1入网电流dq分量

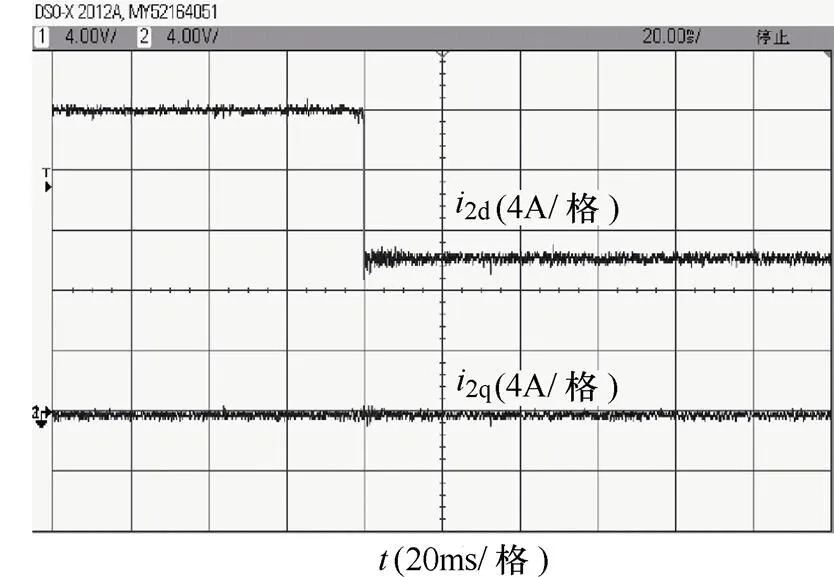
图15 方案2入网电流dq分量

从图13中可以看出，实验过程中，本文所提出策略能够保证实验样机产生较高质量的入网电流且逆变器输出电流与电网电压同相位，单位功率因数为1。由图14～图16所示的三种方案逆变器入网电流dq分量可以看出，在有功指令阶跃变化时，方案1与方案2并未有明显抖动，而方案3出现明显抖动且调整时间较长。总得来说，功率变化时方案1与方案2能有效消除有功功率与无功功率之间的耦合，而方案3无法消除两者之间的耦合。同时由于方案3无法消除有功功率与无功功率之间的耦合，其功率变化时的动态性能也较差。

图16 方案3入网电流dq分量

可以看出，理论分析、仿真结果和实验结果三者相一致，都说明了本文所提出解耦控制策略在保证较高质量的入网电流的同时，消除了有功功率与无功功率之间的耦合。验证了本文中所提出解耦控制策略的可行性和有效性。

4 结论

本文提出了一种基于双电感电流和电容电压反馈的三闭环解耦控制策略，该策略通过状态反馈实现了带LCL型滤波器的三相VSI模型dq分量间的动态解耦。该策略不仅有效消除了有功分量与无功分量间的耦合影响，而且保证了较高的入网电流质量，改善了系统动态性能。仿真和实验均说明了本文所提出控制策略的优越性。

参考文献：

[1] 肖湘宁. 新一代电网中多源多变换复杂交直流系统的基础问题[J]. 电工技术学报, 2015, 30(15): 1-14.

Xiao Xiangning. Basic problems of the new complex AC-DC power grid with multiple energy resources and multiple conversions[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 1-14.

[2] 刘海涛, 吕志鹏, 苏剑, 等. 具有功率精确分配能力的逆变器电压谐波分频下垂控制方法研究[J]. 电力系统保护与控制, 2015, 43(19): 9-14.

Liu Haitao, LüZhipeng, Su Jian, et al. Inverter’s frequency dividing droop controller with accurate load sharing ability[J]. Power System Protection and Control, 2015, 43(19): 9-14.

[3] Gong W, Hu S, Shan M, et al. Robust current control design of a three phase voltage source converter[J]. Journal of Modern Power Systems and Clean Energy, 2014, 2(1): 16-22.

[4] Bao C, Ruan X, Wang X, et al. Design of injected grid current regulator and capacitor-current-feedback active damping for LCL-type grid-connected inverter[C]//IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, 2012: 579-586.

[5] 周国华, 许建平. 开关变换器调制与控制技术综述[J]. 中国电机工程学报, 2014, 34(6): 815-831.

Zhou Guohua, Xu Jianping. Review of switch converter modulation and control technology[J]. Proceedings of the CSEE, 2014, 34(6): 815-831.

[6] 孙绍华, 李春鹏, 贲洪奇. 采用LCL滤波的三相并网逆变器[J]. 电工技术学报, 2011, 26(增1): 108- 112.

Sun Shaohua, Li Chunpeng, Ben Hongqi. Design of three-phase grid-connected inverter with LCL filter[J]. Transactions of China Electrotechnical Society, 2011, 26(S1): 108-112.

[7] 仇克坤, 岳云涛, 李炳华. 浅析LCL滤波器的三相并网逆变器控制技术(英文)[J]. 电工技术学报, 2015, 30(增1): 99-105.

Qiu Kekun, Yue Yuntao, Li Binghua. Study on the three-phase grid-connected[J]. Transactions of China Electrotechnical Society, 2015, 30(S1): 99-105.

[8] Tang Y, Loh P C, Wang P, et al. Exploring inherent damping characteristic of LCL-filters for three-phase grid-connected voltage source inverters[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1433-1443.

[9] 韩刚, 蔡旭. LCL并网变流器反馈阻尼控制方法的研究[J]. 电力系统保护与控制, 2014, 42(17): 72-78.

Han Gang, Cai Xu. Study on feedback damping control methods of grid-connected inverter with LCL filter[J]. Power System Protection and Control, 2014, 42(17): 72-78.

[10] 庄超, 叶永强, 赵强松, 等. 基于分裂电容法的LCL并网逆变器控制策略分析与改进[J]. 电工技术学报, 2015, 30(16): 85-93.

Zhuang Chao, Ye Yongqiang, Zhao Qiangsong, et al. Analysis and improvement of the control strategy of LCL[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 85-93.

[11] Gabe I J, Montagner V F, Pinheiro H. Design and implementation of a robust current controller for VSI connected to the grid through an LCL filter[J]. IEEE Transactions on Power Electronics, 2009, 24(6): 1444-1452.

[12] Loh P C, Holmes D G. Analysis of multiloop control strategies for LC/CL/LCL-filtered voltage-source and current-source inverters[J]. IEEE Transactions on Industry Applications, 2005, 41(2): 644-654.

[13] 胡雪峰, 韦徵, 陈轶涵, 等. LCL 滤波并网逆变器的控制策略[J]. 中国电机工程学报, 2012, 32(27): 142-148.

Hu Xuefeng, Wei Zheng, Chen Yihan, et al. A control strategy for grid-connected inverters with LCL filter[J]. Proceedings of the CSEE, 2012, 32(27): 142-148.

[14] 白志红, 阮新波, 徐林. 基于LCL滤波器的并网逆变器的控制策略[J]. 电工技术学报, 2011, 26(增1): 118-124.

Bai Zhihong, Ruan Xinbo, Xu Lin. Control strategy for the gird-connected inerter with LCL filter[J]. Transactions of China Electrotechnical Society, 2011, 26(S1): 118-124.

[15] 雷亚雄, 李建文, 李永刚. 基于准PR调节器电流双闭环LCL三相并网逆变器控制[J]. 电力系统保护与控制, 2014, 42(12): 44-50.

Lei Yaxiong, Li Jianwen, Li Yonggang. Control strategy of three-phase LCL grid-connected inverter based on quasi-PR adjuster[J]. Power System Protection and Control, 2014, 42(12): 44-50.

[16] Khajehoddin S A, Karimi-Ghartemani M, Jain P K, et al. A control design approach for three-phase grid- connected renewable energy resources[J]. IEEE Transactions on Sustainable Energy, 2011, 2(4): 423-432.

[17] Bao X, Zhuo F, Tian Y, et al. Simplified feedback linearization control of three-phase photovoltaic inverter with an LCL filter[J]. IEEE Transactions on Power Electronics, 2013, 28(6): 2739-2752.

[18] 徐志英, 许爱国, 谢少军. 采用LCL滤波器的并网逆变器双闭环入网电流控制技术[J]. 中国电机工程学报, 2009, 29(27): 36-41.

Xu Zhiying, Xu Aiguo, Xie Shaojun. Dual-loop grid current control technique for grid-connected inverter using an LCL filter[J]. Proceedings of the CSEE, 2009, 29(27): 36-41.

[19] 包献文, 卓放, 谭佩喧. 三相LCL型并网逆变器的模型分析及解耦控制[J]. 西安交通大学学报, 2014, 48(2): 44-49.

Bao Xianwen, Zhuo Fang, Tan Peixuan. Model analysis and decouple control strategy of three-phase grid-connected inverter with an LCL filter[J]. Journal of Xi’an Jiaotong University, 2014, 48(2): 44-49.

[20] Ferreira R J, Araújo R E, Pecas Lopes J A. A comparative analysis and implementation of various PLL techniques applied to single-phase grids[C]// Proceedings of the 2011 3rd International Youth Conference on Energetics (IYCE), Leiria, 2011: 1-8.

[21] Nicastri A, Nagliero A. Comparison and evaluation of the PLL techniques for the design of the grid-connected inverter systems[C]//IEEE Inter- national Symposium on Industrial Electronics, Bari, 2010: 3865-3870.

State Feedback Based Decoupling Control Strategy for Grid-Connected Inverter with LCL Filter

（School of Electrical Engineering Shanghai University of Electric Power Shanghai 200090 China）

Abc to dq transformation, which converts stationary reference frame to synchronous reference frame, is adopted to realize no static error control for three-phase grid-connected voltage source inverter (VSI) with LCL filter. However, this kind of coordinate transformation induces coupling impacts between d-axis and q-axis. Therefore, a three-closed-loop decoupling control strategy based on double-inductor current and capacitor voltage feedback is proposed. The proposed strategy realizes dynamic decoupling process of multiple-input multiple-output (MIMO) time invariant system by state feedback. It can not only effectively eliminate the coupling impacts, but also improve the dynamic performance with the high quality of grid-connected current. Simulation and experimental results have verified the proposed control strategy.

Synchronous reference frame, LCL filter, grid-connected inverter, state feedback, decoupling control

TM464

屈克庆 男，1970年生，博士，副教授，研究方向为电力电子技术及其在新能源和电力系统中的应用。

E-mail: kqqu@shiep.edu.cn（通信作者）

李文旗 男，1991年生，硕士研究生，研究方向为电力电子技术及其在新能源和电力系统中的应用。

E-mail: liwenqishiep@163.com

2016-01-11 改稿日期 2016-03-17

上海绿色能源并网工程技术研究中心资助项目（13DZ2251900）。