填充墙对钢筋混凝土框架结构周期折减系数的影响

刘延生，车德路，宋国华，任贺贺

（郑州大学，河南 郑州 450001）

填充墙对钢筋混凝土框架结构周期折减系数的影响

刘延生，车德路，宋国华，任贺贺

（郑州大学，河南 郑州 450001）

以填充墙的填充率为变量，建立了5个6层5×3跨的框架结构模型，通过数值分析,同时考虑填充墙的重量和刚度影响,并采用填充墙产生初始裂缝时的刚度进行折减,得出填充墙框架结构周期折减系数与填充率的关系,并提出周期折减系数的建议取值范围为0.4～0.85，该取值范围小于规范规定值。

钢筋混凝土框架结构；填充墙；填充率；周期折减系数

在我国，框架结构仍然是最主要的结构体系之一。汶川地震后的震害实例调查表明[1],框架结构房屋除了部分主体结构的破坏外,填充于框架内墙体的破坏也较为普遍且严重。现在的主流框架结构计算方法是先建立框架结构模型，填充墙以荷载的形式输入。然而实际情况与研究均证明在水平力作用下填充墙是一种受力构件，无论是强度和刚度都相对较高的砖墙，还是相对柔弱的轻质砌块，它们在水平荷载作用下都对结构的侧移刚度有较大的影响，会使结构刚度明显增大[2]，特别是结构早期刚度。结构刚度的增大会使结构自振周期减小，从而使作用在整个建筑上的水平地震作用增大，增大幅度高的可达到50%左右[3]。而且结构质量、自振周期及整体或局部的变形和位移都会有所变化[4、5]。

除了刚度效应外，填充墙还会对主体结构的梁、柱、墙产生约束效应，使得主体结构构件的变形受到一定程度的限制，并有可能减小梁、柱、墙的计算高度。由于填充墙与框架结构之间的相互作用，使得从结构开始加载直到破坏的整个受力和变形过程比较平缓，与填充墙的脆性不同，结构具有较好的延性。

填充墙的存在会改变框架结构的动力特性。因此，进行填充墙对框架结构动力特性影响的研究,更好地把握结构的实际动力特性和动力反应特点,对于有效减少框架结构在地震作用下的破坏,降低震害造成的经济损失有着重要的理论意义和实践价值。

本文采用计算机建立数值模型，通过运用控制变量法，改变某一变量，比较各个模型的试验结果，从而得到一定的结论。

建立了5个6层横向5跨纵向3跨的模型，底层高均为3.9m，其余层高为3m。框架柱距为6m，框架梁尺寸为650mm×250mm，框架柱尺寸为500mm× 500mm，楼板厚度为120mm，填充墙厚度为240mm，混凝土强度C30，填充墙材料为普通烧结砖，其初始弹性模量E0=7534.72MPa，考虑刚度折减[6]，用初始裂缝时的刚度，计算弹性模量E=1.5×106kN/m2，泊松比v=0.15，线膨胀系数a=5×10-6/C，容重r=18kN/m3。楼面恒荷载取1kN/m2，活荷载取2kN/m2，屋面活荷载取0.5kN/m2，女儿墙荷载取3.375kN/m。反应谱作用只取水平面作用，放大系数取1.5。地震信息如下：分组第一组，地震烈度7度（0.15g），场地类型II类，多遇地震，阻尼比0.05，采用平扭藕联CQC法，振型考虑正负号，支座采用固端约束。

建立模型1为纯框架，模型2、3、4为部分填充墙，其填充墙的填充率如表1所示，模型5为满布填充墙情况。模型1～模型4的结构布置如图1所示，其中模型2～模型4由于每层填充墙都一样，图中仅显示一层。模型5为全部填充墙结构，不再列图表示。

各模型填充墙的填充率（%） 表1

各模型前六阶模态对应的周期情况如表2所示，各模型对应的模态周期变化规律如图2所示。从图表可以看出，只有模态1、2、3是主要模态，且每3个模态为1组，周期接近。同一模型的第四阶振型与第三阶振型的周期比见表3。由表3可知，第四阶模态周期相对第三阶周期衰减很大，且由于能量总是从低阶振型向高阶振型传递，所以只取前三阶振型就可以正确分析，满足要求。

图1 模型的结构布置图

将各模型的模态周期随模态阶数的变化规律绘出，见图3所示。由图3知：纯框架的第三阶振型与第四阶振型变化相对框架填充墙要大的多，斜率很大；而框架填充墙结构填充率对第三阶振型与第四阶振型周期影响不大，斜率基本相同。说明纯框架结构能量耗损较之框架填充墙结构要迅速[7]。

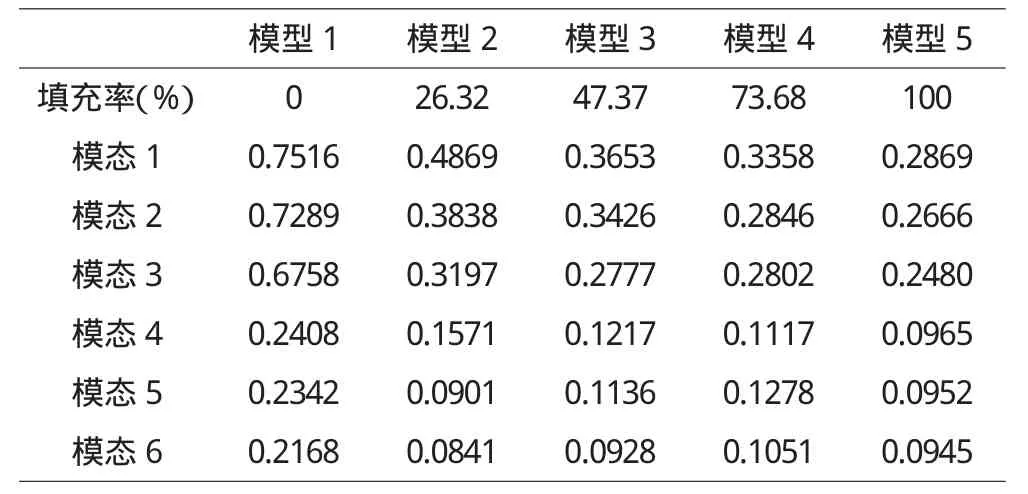
各模型对应的前6阶模态的周期（s） 表2

图2 模型前6阶模态周期（s）

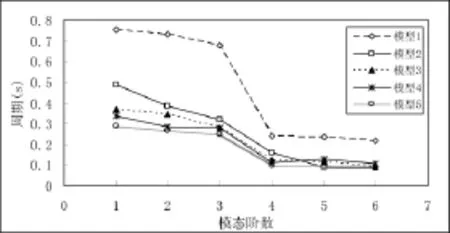
图3 各模型的模态周期随模态阶数的变化规律

同一模型的第四阶振型与第三阶振型的周期比 表3

定义周期折减系数为填充墙结构的周期与相应纯框架结构的周期的比值，其中前三阶模态周期折减系数见表4，并绘出周期折减系数与填充墙填充率的关系见图4。

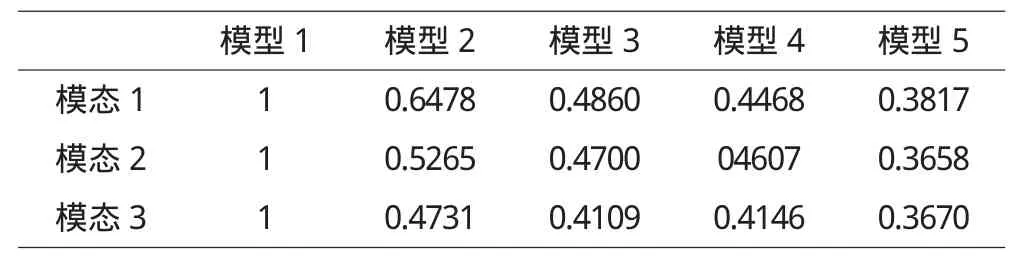
各模型前三阶模态的周期折减系数 表4

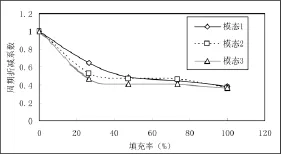
图4 周期折减系数与填充率的关系

由图4可知，前三阶模态的周期折减系数随着填充墙填充率的增大而减小，但是填充率较小时影响较大，特别是填充率小于40%时变化很快，大于40%以后，周期折减系数变化很小，基本稳定在0.4～0.5之间。

考虑到模型1和模型5的填充率为0和100%这两种极端情况，在实际工程中不可能存在，建议周期折减系数的最小值可以取为0.4。由图4可以看出当填充率为10%时，周期折减系数大致可以取为0.85。所以，建议多层框架结构粘土砖填充墙的周期折减系数的取值范围为：0.4～0.85。

综上所述，同时考虑填充墙刚度和质量，得到的周期折减系数在0.4～0.85。规范建议当主要考虑填充墙的刚度影响时，折减系数可0.6～0.7；根据填充墙的多少、填充墙开洞情况，其对结构自振周期影响的不同，可取0.5～0.9。可以看出本文的研究结果小于规范建议的周期折减系数建议值。需要说明的是本结论是用折减刚度计算求得的，其中计算刚度采取的填充墙初始裂缝时的刚度，即为初始刚度的0.2倍。可想而知如果用初始刚度，则周期折减系数会更小，所以填充墙刚度是设计师不可忽略的因素，否则会埋下重大安全隐患。

TU311.3

A

1007-7359（2016）05-0210-02

10.16330/j.cnki.1007-7359.2016.05.074

刘延生（1972-），男，河南鲁山人，毕业于郑州工业大学，学士；高级工程师，国家注册一级建造师。