基于多核稀疏编码的三维人体姿态估计

余家林，孙季丰，李万益

(华南理工大学电子与信息学院，广东广州 510641)



基于多核稀疏编码的三维人体姿态估计

余家林，孙季丰，李万益

(华南理工大学电子与信息学院，广东广州 510641)

为了准确有效的重构多视角图像中的三维人体姿态，该文提出一种基于多核稀疏编码的人体姿态估计算法.首先，针对连续帧姿态估计的歧义问题，该文设计了一种用于表达多视角图像的HA-SIFT描述子，其中，人体局部拓扑、肢体相对位置及外观信息被同时编码；然后，在多核学习框架下建立同时考虑特征空间内在流形结构与姿态空间几何信息的目标函数，并在希尔伯特空间优化目标函数以更新稀疏编码、过完备字典与多核权值；最后，利用姿态字典原子的线性组合来估计对应未知输入的三维人体姿态.实验结果表明，与核稀疏编码、Laplace稀疏编码及Bayesian稀疏编码相比，文本方法具有更高的估计精度.

人体姿态估计；多视角图像；多核学习；稀疏编码；字典学习

电子学报URL:http://www.ejournal.org.cn DOI:10.3969/j.issn.0372-2112.2016.08.019

1 引言

从多视角序列估计含三维空间位置信息的人体姿态在计算机视觉领域有广泛应用，譬如手势识别[1]、行为识别[2]、运动捕捉[3]和人机交互[4]等.该研究虽已取得重大突破，但仍有许多具有挑战性和亟待解决的难题.首先，复杂的三维人体运动与二维图像之间存在语义鸿沟，深度信息的缺乏导致估计的人体姿态存在歧义；其次，人体外观与轮廓在帧间差异较大，给肢体的定位带来困难；最后，肢体的遮挡、姿态数据的高维及场景光线的变化等，都使人体姿态估计成为一项艰巨的任务.常见方法分3类：基于模型的方法，其依赖一种基于先验知识的人体模型，通过优化目标函数来估计人体姿态，但计算量较大[5]；基于学习的方法，其直接学习从特征空间到姿态空间的映射[6]，但它对姿态的判别是以庞大的训练数据为前提；基于样本的方法，其在训练数据库中检索与输入最相似的数据，并利用该数据插值来获取结果，该方法同样依赖庞大的训练数据，且要求训练数据要覆盖姿态空间尽可能多的自由度[7].

最近，在机器学习和模式识别领域中兴起了一种被称为稀疏编码[8]的算法，譬如人脸识别[8]、目标分类[9]和人体姿态估计[10]等.Behnam等[11]在Bayesian框架下提出一种稀疏编码算法(Bayesian Sparse Coding,BSC)，通过学习两种过完备字典克服了小样本问题所导致的过拟合.Gao等[12]提出一种Laplace稀疏编码算法(Laplace Sparse Coding,LSC)，解决了数据位置和相似度信息丢失问题，但原始空间的特征往往带噪声，在该空间构造的正则项，未必能精确反映数据的内在流形.2013年，Gao等[13]提出一种能捕捉特征非线性相似度的核稀疏编码算法(Kernel Sparse Coding,KSC)，打破了仅在原始空间编码的模式.但对不同类型的输入，采用单一核函数来处理并不合理，且面临核函数及参数选择难题.

人体姿态估计中的样本是高维非线性的，尽管样本的近邻点可在线性距离上被找到，但由它们所构造的近邻图并不能精确反映数据的内在流形，而该流形在许多应用中又非常重要.核技巧把原始数据隐式映射至希尔伯特空间克服了该问题，但又面临核函数及参数的选择难题，交叉验证方法虽可解决该难题，但计算量过大.综合考虑，本文提出一种多核稀疏编码算法(Multi-Kernel Sparse Coding,MKSC)，通过引入多核学习，既解决了姿态数据的“维数灾难”问题[14]，又可应对样本的非线性.其中，最优核由核函数集中核函数的线性组合导出，从而不存在核函数及参数的选择难题.

2 基于多核稀疏编码的人体姿态估计

本文算法框架如图1所示，它从三方面提升了姿态估计精度.首先，将含肢体局部拓扑、位置及外观信息的SIFT算子作用于图像兴趣点，并借助词袋模型[15]描述图像，打破了以往仅编码单目轮廓的模式；其次，用多核函数将数据隐式映射至希尔伯特空间，使得构造的近邻图能够精确反映数据内在流形；最后，在稀疏编码过程中考虑姿态特征几何信息，使肢体的局部拓扑在运动过程中被有效保持.

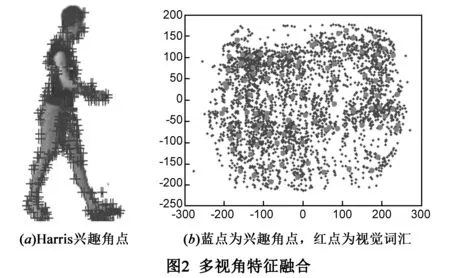
2.1 多视角特征融合

人体姿态估计精度高度依赖于图像的表达，人体轮廓特征虽为姿态估计提供强有力的形状线索，且对人体外观及光线具有不变性，但轮廓特征丢失了外观信息，而该信息对连续帧姿态之间微小的变化又十分敏感，这在连续帧姿态估计中容易造成歧义.为解决该问题，本文通过如下四步设计一种特殊的描述子：

(1)前景提取：通过背景差分获取多视角序列的人体形状边界窗body.

(2)提取Harris兴趣角点：在人体形状边界窗body内提取Harris兴趣点.

(3)SIFT算子：将肢体局部拓扑、位置及外观信息编码至SIFT算子，并作用于兴趣点得p.

(4)HA-SIFT描述子：找到兴趣点的相对位置(u,v)，生成HA-SIFT描述子：s=(u,v,p)T；

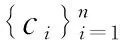
2.2 多核稀疏编码

2.2.1 建立目标函数

假设有m个训练样本对，ξ=[(x1,y1),…,(xm,ym)]，其中，[x1,…,xm]=X，表示输入特征矢量集，且xi=[xi1,…,xin]T∈n；[y1,…,ym]=Y，表示与X对应的m个姿态特征矢量集，且yi=[yi1,…,yir]Tr.在多核学习[14]框架下，利用核函数将原始输入空间隐式映射至高维再生希尔伯特空间(Reproducing Kernel Hilbert Space,RKHS)H(l)，该空间拥有非线性映射函数φ:X→H的内积〈·,·〉，即：〈φ(x),φ(y)〉=K(x,y).本文假设选用L个核函数，从而对应L个希尔伯特空间，但通常并不明确选用哪个空间，最合理的做法是级联这L个空间，从而形成增广再生希尔伯特空间，并通过迭代优化空间H(l)的权值≥0,∀，得最适合输入的空间.假设映射函数φ：ζi→φl(ζi)，l=1,…,L，φl为H(l)的映射函数，级联这L个函数：φτ(ζi)=[τ1φ1(ζi),…,τLφL(ζi)]T，其中，等同于H(l)的权值，确保级联后的映射函数φτ(ζi)也达到最优，且≥0,∀l，则样本对(ζi,ζj)的核函数可表示为如下式子：

(1)

当原始空间的特征被映射至希尔伯特空间后，将样本对(xi,yi)用(φτ(xi),φτ(yi))代替，输入特征字典DF∈n×k和人体姿态字典DP∈r×k分别用φτ(DF)和φτ(DP)代替.但核函数Kτ(DP,yi)，Kτ(DP,DP)，Kτ(DF,xi)和Kτ(DF,DF)的计算量过大.为解决该问题，假设输入特征和人体姿态特征的基元跨越在φτ(X)=[φτ(x1),…,φτ(xm)]和φτ(Y)=[φτ(y1),…,φτ(ym)]的列空间中，输入特征字典和姿态字典分别表示为：DF=φτ(X)·A和DP=φτ(Y)·B，其中，A∈m×k和B∈m×k为跨越参数矩阵.目标函数如下所示：

(2)

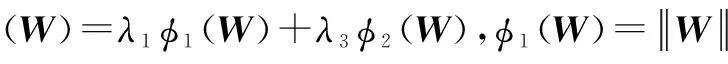
(3)

2.2.2 人体姿态空间转换

姿态字典DP∈r×k中含关节角度数据∈[-180°,180°]，使重构误差不能用l2范数度量.图3显示了两种人体姿态，它们手部空间位置很接近，但在角度空间中差异却很大.因此，本文采用一种映射将姿态矢量φi∈DP转换至一个2r的单位球面空间，记为：

(4)

2.3 优化目标函数

2.3.1 更新稀疏编码W

为了独立更新稀疏编码矢量wi，将目标函数改写为矢量形式，记为：

(5)

除wi以外的所有矢量{wj}j≠i都是固定的，可将式(5)进一步改写为：

(6)

2.3.2 更新跨越参数矩阵A和B

为了更新跨越参数矩阵A，现固定稀疏编码W、跨越参数矩阵B与多核权值τ，移除目标函数中的无关项，得如下式子：

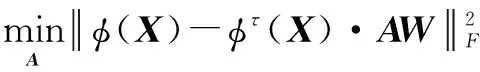
(10)

式(10)是一个带二次约束的最小二乘问题，可采用一般的基于迭代投影的梯度下降法求解.为提高算法性能，本文提出一种更加高效的基于拉格朗日对偶方法.

(11)

假设Λ为一个k×k的对角阵，且Λii=δi，这样L(DF,δ)可表示为：

+Tr(ATφ(X)Tφ(X)AΛ)-cTr(Λ)

(12)

对于式(12)而言，令∂L(DF,δ)/∂A=0可得出最优解A'，即：

∂L(DF,δ)/∂A=-2Kτ(X,X)WT+2WTKτ(X,X)WA

+2Kτ(X,X)ΛΑ

=0

(13)

A'=Kτ(X,X)WT·(WTKτ(X,X)W+Kτ(X,X)Λ)-1

(14)

将式(14)代入式(12)，拉格朗日对偶函数变为：

g(δ)= Tr(Kτ(X,X))-Tr(Kτ(X,X)WT(WWT

+Λ)-1W)-cTr(Λ)

(15)

通过解决如下一个拉格朗日对偶问题计算最优解Λ*：

s.t.δi≥0,i=1,…,k

(16)对于式(16)而言，可以直接采用牛顿法或梯度下降法计算最优解Λ*，代入式(14)得到最优的跨越参数矩阵A*=Kτ(X,X)WT·(WTKτ(X,X)W+Kτ(X,X)Λ*)-1.

2.3.3 更新多核权值τ

学习权值τ是为从核函数集中构造最优核来处理不同类型的输入，以提高系统的泛化性能.现固定稀疏编码W、跨越参数矩阵A和B，移除目标函数的无关项，得如下式子：

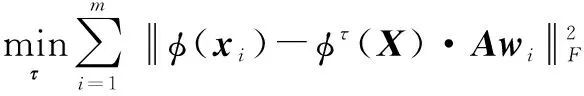
(17)

式(17)可被视为一个关于权值τ的带约束QP问题，即：

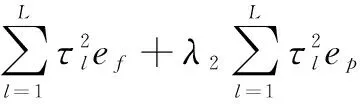
(18)

式(18)中，ef和ep可分别表示为：

(19)

将式(19)代入式(18)，求解一个标准的QP问题来更新权值τ.为提高算法效率，本文采用一种对偶作用集算法[18]在可行域内搜索解析解来实现该类问题的优化.

2.4 三维人体姿态估计

3 实验分析

3.1 多视角人体姿态估计

为了验证算法的有效性，本文在布朗大学的Brown与HumanEva数据库[19]上实验.其中，Brown库中含1184帧Lee环绕行走的C1～C4四视角灰度图像序列；HumanEva库中含(S1,S2,S3)的人体环绕行走姿态共2950帧、慢跑运动2345帧、拳击运动2486帧及其手势动作2850帧.由C1～C4灰度摄像机和C1～C3彩色摄像机采集而来.两数据库中图像尺寸分别为：644×484和656×490.

实验中取HumanEva-Ⅰ的C1～C3三个视角、Brown与HumanEva-Ⅱ的C1～C4四个视角.并分别选取10与15肢体人体模型，包括：头部、躯干、左右上下手臂、左右大小腿，后者增加了骨盆、左右手及左右脚.本文实验环境为：CPU:SU3500，2G内存，用Matlab 2012a仿真实验.本文分别从两方面验证算法有效性，一比较多核学习框架下与一般非监督学习框架下稀疏编码对人体姿态估计的影响；二比较HA-SIFT、SIFT及轮廓特征对算法性能的影响.

图4为从C1～C4四视角观察Brown库中环绕行走姿态估计结果.并将本文方法(MKSC)与Bayesian稀疏编码[11](BSC)、Laplace稀疏编码[12](LSC)及核稀疏编码[13](KSC)进行比较.

图5为从HumanEva中挑选出的部分实验结果：S1(Gesture)、S2(Walking)及S3(Jogging).在原始的HumanEva-Ⅰ数据库中，是采用10肢体的人体模型，本文将其扩展至15肢体.

针对图4的实验结果，对包含本文算法在内的四种算法进行对比分析：

(1)MKSC算法利用多核将输入特征隐式映射至希尔伯特空间，在该空间构造的近邻图能精确反映数据内在流形，并解决了样本的“维数灾难”及非线性问题.该算法采用多核融合导出的最优核，能适应各种类型的输入，该方法估计出的人体姿态效果最佳；

(2)KSC算法针对多种类型的输入仅采用单一核函数来处理，存在核函数及参数选择难题.人们往往是依据输入特征分布来确定最适宜的核函数.但当难以确定输入特征分布时，核函数的选取存在很大的随机性，导致KSC算法的泛化性能较差，估计误差也较大；

(3)LSC算法是直接在原始空间构造近邻图，没有考虑输入空间的噪声及样本的非线性，使构造的近邻图没能够精确反映数据的内在流形.另外，LSC的解偏向于一个常数，Laplace矩阵的嵌入并不能很好保存肢体的局部拓扑，外推能力较弱，姿态估计误差较大.

(4)BSC算法未考虑人体姿态数据的局部几何信息，而这些信息又是人体姿态估计中不可或缺的，这往往会导致肢体之间的局部拓扑在人体运动中不能被有效保持.实验结果显示，该算法估计出的人体右臂出现严重畸变，且各肢体间的连接不协调甚至不成人形.

由此得出结论，在多视角人体姿态估计问题上，本文算法比现有最新算法更具优势.

图6为MKSC分别基于三类特征的邻帧姿态估计结果，本文采用15肢体人体模型在HumanEva-Ⅱ的S2(Walking)上实验.实验结果表明，HA-SIFT克服了因自遮挡所导致的歧义(正常：左肢黄右肢青，歧义：左肢青右肢黄)，且估计精度也明显提高.

3.2 人体姿态估计误差

表1列出了本文算法与其它三种算法分别基于HA-SIFT，SIFT及轮廓特征的关节角度的均方根误差[5](RMS)，在行走(Walking)、拳击(Boxing)、慢跑(Jogging)及手势(Gesture)四类数据集上实验.估计姿态y与真实数据y′的RMS误差D(y,y′)如下所示：

(20)

图7显示了在四种算法作用下，分别基于三类特征在HumanEva-Ⅰ的S3(Jogging)数据集上实验所得到的对约定角度变量Angle∈[1,…,20]的关节角度相对误差.

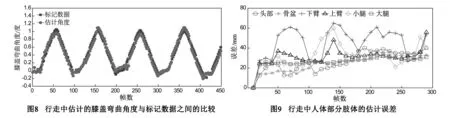
实验结果表明，在约定角度Angle∈[1,…,20]内，本文算法对多种类型的输入泛化性能强，并且本文的HA-SIFT特征在人体姿态估计问题上效果最佳，相对误差在3种特征中是最小的.图8为行走过程中本文算法估计的膝盖弯曲角度与标记数据之间的偏差.

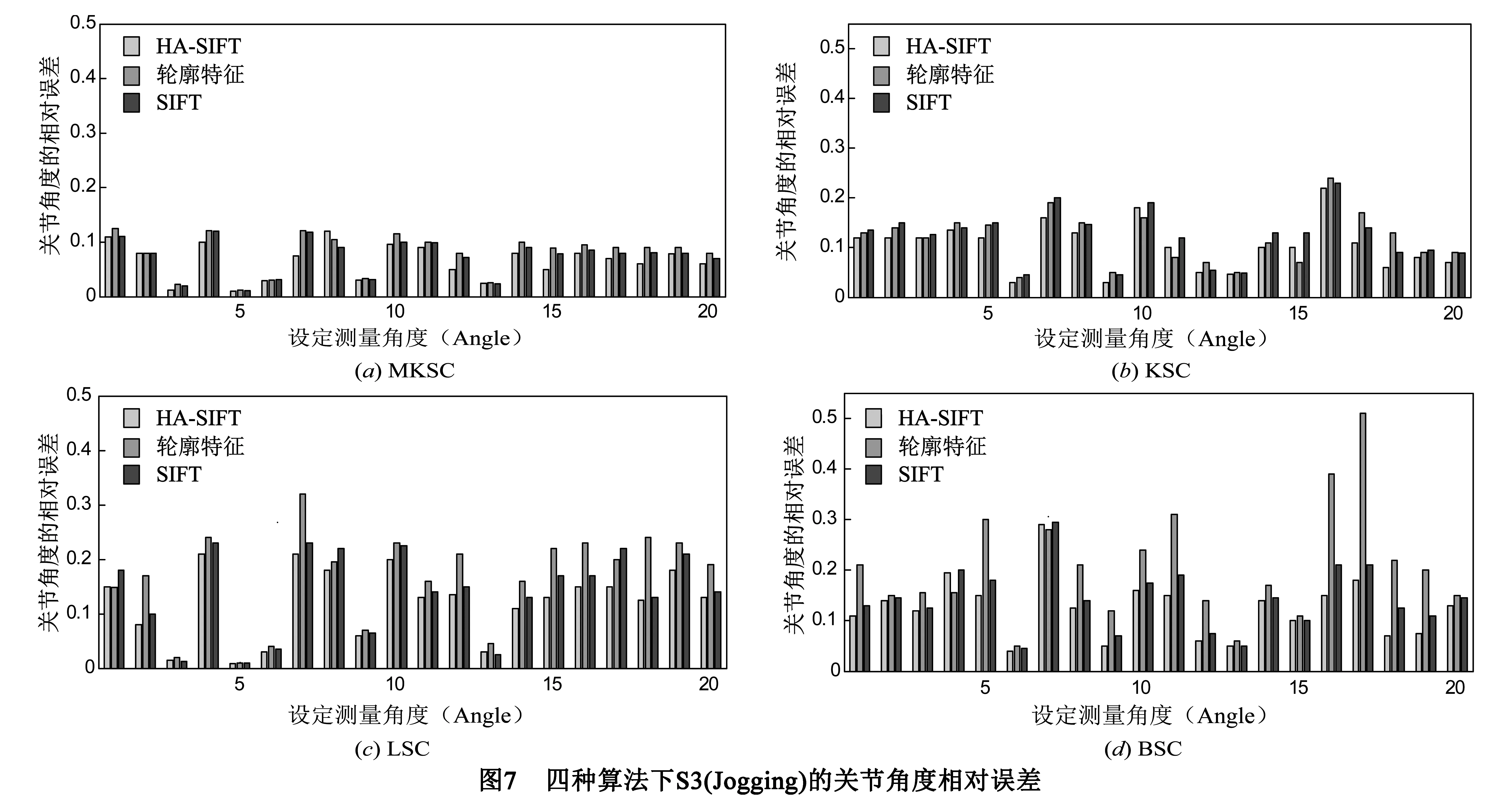
表1 行走、拳击、慢跑及手势四类数据集上的关节角度RMS误差(单位：度)

HA-SIFT特征SIFT特征轮廓特征行走拳击慢跑手势行走拳击慢跑手势行走拳击慢跑手势MKSC3.84523.03012.35312.76304.21023.65362.70132.81834.71934.85373.62173.2021KSC5.66274.36124.19213.96366.08635.65725.71435.89116.21316.16465.86616.1129LSC7.19446.25615.29715.74507.36406.33125.62396.85357.44456.97846.32556.3614BSC8.37097.21457.29156.71428.81358.27856.86187.27159.14678.46617.54977.4610

为了评价估计姿态的空间位置误差，参照文献[19]的方法，用肢体中各关节误差的均值作为每帧的估计误差.图9显示了前300帧中人体头部、骨盆、上下手臂及大小腿的估计误差.图10表示在单视角与四视角下本文算法与其它三种算法的行走姿态估计误差.

为了测试本文算法的抗噪能力.在实验中分别设定6种椒盐噪声密度：0%，10%，20%，30%，40%，50%.图11为在6种噪声强度干扰下的外观图像.图12为前300帧在6种噪声密度下行走姿态估计误差.

随噪声密度由0%增大至40%，估计误差逐渐增大，但从整体观察，仍处于较低水平.当噪声密度增大至50%时，估计误差异常偏大，表明算法已失效，本文算法在一定噪声强度范围内具有较强的鲁棒性.

3.3 算法的复杂性分析

本节主要讨论多核稀疏编码算法的计算复杂度与姿态估计精度之间的关系.假设共有m个训练样本对，ξ=[(x1,y1),…,(xm,ym)]，其中，xi∈n，yi∈r.在权值特征空间找到k个最近邻的计算复杂度为：O(m2)，其中，k等于m；固定矩阵A，B及权值τ，更新W的计算复杂度为：O(nm2J)，J为很小的正整数，表示W中非零元数目，则可近似为：O(nm2)；固定矩阵A，B及W，更新权值τ的计算复杂度为：O(k3Lm)，其中，L表示核函数的个数；固定W及权值τ，更新矩阵A与B的计算复杂度为：O(n3)与O(r3).那么，知整个算法的计算复杂度为：O(m2+t(nm2+Lm4+n3+r3))∝m,n.其中，t为迭代次数，r为姿态特征的维度.图13为在不同给定特征维度n下，手势姿态估计精度随训练样本数m的变化趋势.

4 结论

为了准确有效的重构多视角图像中的三维人体姿态，本文提出一种基于多核稀疏编码的三维人体姿态估计算法.该算法结合Harris兴趣角点与SIFT算子来生成本文的HA-SIFT描述子，并借助词袋模型来描述输入图像，打破了以往仅编码单目轮廓特征的模式；由于数据可能为非线性分布，直接在原始空间构造的流形正则项并不可靠，本文利用核函数将原始数据隐式映射至希尔伯特空间，使该空间的流形正则项能精确反映数据的内在流形结构.与目前最新算法相比，本文算法具有更高的估计精度.但由于目前仍采用刚性的人体模型，在估计复杂姿态时效果并不理想.在接下来的研究中，将试图采用点云配准方法代替基于能量的方法，用点云数据建模人体，有望进一步提高估计精度.

[1]Zhu Ren,Yuan Junsong,Meng Jingjing,et al.Robust part-based hand gesture recognition using kinect sensor[J].IEEE Transaction on Multimedia,2013,15(5):1110-1120.

[2]Lin Weiyao,Chen Yuanzhe,Wu Jianxin,et al.A new network-based algorithm for human activity recognition in videos[J].IEEE Transaction on Circuit and System for Video Technology,2014,24(5):826-841.

[3]S Vantigodi,W B Radhakrishnan.Action recognition from motion capture data using meta-cognitive RBF network classifier[A].Proceedings of IEEE International Conference on Intelligent Sensors,Sensor Networks and Information Processing(ISSNIP)[C].Singapore:IEEE Computer Society,2014.1-6.

[4]G Palmas,M Bachynskyi,A Oulasvirta,et al.MovExp:A versatile visualization tool for human-computer interaction studies with 3D performance and biomechanical data[J].IEEE Transaction on Visualization and Computer Grapgics,2014,20(12):2359-2368.

[5]A Agarwal,B Triggs.Recovering 3D human pose from monocular images[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2006,28(1):44-58.

[6]J Shotton,R Girshick,A Fitzgibbon,et al.Efficient human pose estimation from single depth images[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2013,35(12):2821-2839.

[7]N C Tang,Chiou-Ting Hsu,Weng Mingfang,et al.Example-based human motion extrapolation and motion repairing using contour manifold[J].IEEE Transaction on Multimedia,2014,16(1):47-59.

[8]Wang Jing,Lu Canyi,Wang Meng,et al.Robust face recognition via adaptive sparse representation[J].IEEE Transaction on Cybernetics,2014,44(12):2368-2378.

[9]王瑞,杜林峰,孙督等.复杂场景下结合SIFT与核稀疏表示的交通目标分类识别[J].电子学报,2014,42(11):2129-2134.

WANG Rui,DU Lin-feng,SUN Du,et al.Traffic object recognition in complex scenes based on SIFT and kernel sparse representation[J].Acta Electronica Sinica,2014,42(11):2129-2134.(in Chinese)

[10]Zhou Liuyang,Lu Zhiwu,Howard Leung,et al.Spatial temporal pyramid matching using temporal sparse representation for human motion retrieval[A].Proceedings of International Conference on Computer Graphics International(CGI)[C].Sydney,Australia:Springer,Berlin,2014.845-854.

[11]B M Behnam,A Jourabloo,A Zarghami,et al.A Bayseian framework for sparse representation-based 3D human pose estimation[J].IEEE Signal Processing Letters,2014,21(3):297-300.

[12]Gao Shenghua,I W Tsang,Chia Liang-Tien.Laplace sparse coding,Hypergraph laplacian sparse coding,and application[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2013,35(1):92-101.

[13]Gao Shenghua,I W Tsang,Chia Liang-Tien.Sparse representation with kernels[J].IEEE Transaction on Image Processing,2013,22(2):423-434.

[14]Hong Zeng,Yiu-ming Cheung.Feature selection and kernel learning for local learning-based clustering[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2011,33(8):1532-1546.

[15]赵宏伟,李清亮,刘萍萍.基于分级显著信息的空间编码方法[J].电子学报，2014,42(9):1863-1867.

ZHAO Hong-wei,LI Qing-liang,LIU Ping-ping.Spatial encoding based on hierarchical salient information[J].Acta Electronica Sinica,2014,42(9):1863-1867.(in Chinese)

[16]Edgar,Simo-Serra,A perez-Gracia.Kinematic synthesis using tree topologies[J].Mechanism and Machine Theory,2014,72(2):94-113.

[17]Y Xia,S Changyin.A novel neural dynamical approach to convex quadratic program and its efficient application[J].Neural Network,2009,10(22):1463-1470.

[18]Fan Qibin,Jiao Yuling,Lu Xiliang.A primal dual active algorithm with continuation for compressed sensing[J].IEEE Transaction on Signal Processing,2014,62(23):6274-6284.

[19]L Sigal,and M J Black.Humaneva:synchronized video and motion capture dataset for evaluation of articulated human motion[R].Report of Brown University,Providence:2006.

余家林(通信作者) 男，1989年生于贵州镇远.现为华南理工大学电信学院信息与通信工程专业博士研究生.研究方向为计算机视觉、人体运动形态分析、图像与视频处理等.

E-mail:yu.jialin@mail.scut.edu.cn

孙季丰 男，1962年生于广东揭阳，现为华南理工大学电信学院教授，博士生导师.研究方向包括智能信号处理、图像与视频处理、自组织通信网等.

3D Human Pose Estimation Based on Multi-kernel Sparse Coding

YU Jia-lin,SUN Ji-feng,LI Wan-yi

(SchoolofElectronicandInformationEngineering,SouthChinaUniversityofTechnology,Guangzhou,Guangdong510641,China)

In order to reconstruct 3D human pose from multi-view images accurately and effectively,a novel human pose estimation algorithm based on multi-kernel sparse coding is proposed.First,for the ambiguity of human pose estimation between the consecutive frames,we describe multi-view images using a special HA-SIFT descriptor,in which the human body local topology,relative coordinates and appearance information are encoded simultaneously;then,an objective function is established within the framework of multi-kernel learning,it takes both intrinsic manifold structure of the feature space and geometrical information of the pose space into consideration.The sparse coding,over-complete dictionary and multi-kernel weight are updated by optimizing the objective function iteratively in the Hilbert space;finally,the corresponding 3D human pose of the unknown input image is estimated by a linear combination of the bases of the human pose dictionary.The experimental results show that our proposed method provides higher accuracy of human pose estimation compared with kernel sparse coding,Laplace sparse coding and Bayesian sparse coding.

human pose estimation;multi-view images;multi-kernel learning;sparse coding;dictionary learning

2015-01-20；

2015-04-06；责任编辑：马兰英

国家自然科学基金青年科学基金(No.61202292);广东省自然科学基金(No.9151064101000037)

TP391.4

A

0372-2112 (2016)08-1899-10