军用飞机任务保障规划方案效率分析
崔建国,谢建文,于明月,徐晓宇,王瑞凯
(1.沈阳航空航天大学 自动化学院,沈阳 110136;2.沈阳飞机设计研究所,沈阳 110035)
军用飞机任务保障规划方案效率分析
崔建国1,2,谢建文1,于明月1,徐晓宇2,王瑞凯2
(1.沈阳航空航天大学 自动化学院,沈阳 110136;2.沈阳飞机设计研究所,沈阳 110035)
针对军用飞机再次出动保障任务规划方案的效率分析缺乏有效的解决方法的问题,构建了基于灰色聚类算法与熵权法相结合的任务保障规划方案效率分析模型;该模型首先利用灰色聚类对保障方案的人员利用率的有效参数进行计算并确定;其后利用熵权法对保障方案的人员数量时间分布进行计算;在此基础上根据任务规划工期、人员利用率、人员数量时间分布3个参数的权重得到任务保障规划方案效率;文中通过实例对构建的效率分析模型进行了验证;结果表明:所构建的效率分析模型能够有效的对军用飞机任务保障规划方案效率分析,且具有较高的可靠性和很好的工程应用价值。
效率分析;灰色聚类;熵权法;白化权函数;权重
0 引言
军用飞机任务保障规划方案效率分析是军用飞机保障任务规划的最后一个环节,也是检测军用飞机保障任务规划方案优劣的评判依据。合理的任务规划方案能够使的军用飞机保障任务规划效率得到提升。对军用飞机任务规划方案进行效率分析,可为实际保障工作提供理论参考和指导,是保障飞机再次出动高效完成的关键,在一定程度上决定着战斗的胜负,具有重要的研究价值和军事意义。
目前,对任务规划方案的效率分析常用的方法有:数据包络分析法、模糊层次分析法、灰色关联分析法。但是,针对军用飞机再次出动保障任务规划方案的效率分析尚缺乏有效的解决方法,文献[1] 提出了DEA交叉效率评价的方法,通过建立两阶段交叉效率评价模型和样本数据做出样本式的评价过程。由于DEA 模型存在只能将决策单元区分为有效与非有效的局限性,并不能有效的解决军飞机任务规划方案的效率分析。
本文提出了一种结合灰色聚类和熵权法组合赋权的方法,对保障任务规划方案进行了效率分析。有效的解决了多因素影响下对方案的效率分析。
1 任务保障规划方案效率分析理论基础
1.1 灰色聚类算法理论
设有n个聚类对象,m个聚类指标,s个不同灰类,根据第i(i=1,2,…,n)个对象关于j(j=1,2,…,m)指标的观测值xij(i=1,2,…,n;j=1,2,…,m),将第i个对象归入第k(k∈{1,2,...,s})个灰类,称为灰色聚类[2]。
依据对灰色系统理论的分析,以及结合白化权函数的具体概念及所表达的含义,可将白化权函数分为典型、下限测度、适中测度、上限测度等形式的白化权函数,根据任务的实际需求采用典型白化权函数。
典型白化权函数记为:
可给出其具体形式的计算公式如下:
1.2 熵权法理论
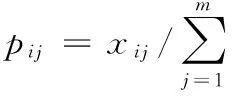
对于系统中的某个指标xj,其信息熵为:
(1)
式中,k=1/lnn。
可以看出:如果某个评价指标的信息熵越小,就表明其指标值的变异程度越大,提供的信息量也就越多,在综合评价中所起的作用越大,则其权重也应越大;反之亦然[4。
2 任务保障规划方案效率分析模型的构建
对军用飞机保障任务规划方案制定后,对方案的效率分析主要参考任务规划工期、人员利用率、人员数量时间分布这3个有效参数。工期的时间长短对军用飞机再次出动发挥作战效能起着至关重要的作用;人员的使用率能够显示出人员分配是否均匀,均衡度的提高更显人性化的安排;每时刻人员使用平均,避免某一时刻人员过度集中,使安排人员上可能会有更多的可选择性。先对能够充分反应规划工期、人员利用率、人员数量时间分布的各指标参数进行分析(即一级分析),得到这3个参数的有效值,然后对3个参数分配相应的权重进行二级分析。构建如图1所示的任务保障规划方案效率分析模型。
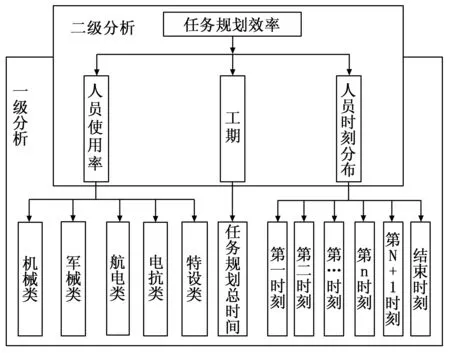
图1 任务保障规划方案效率分析模型
3 军用飞机任务保障任务规划的效率分析
3.1 人员利用效率分析
现有资源分别为军械类、机械类、航电类、电抗类、特设类五类人员,每类人员分别有师和员两种类别。如军械类有军械师、军械员两种人员。每类人员数量如表1所示。

表1 每类人员数量
不同的任务规划方案选择的人员使用情况会有区别,因此对于人员利用效率会产生影响。在安排人员时尽量使每一类资源都均衡利用,在分析人员利用率时应该对各类之间的利用率进行效率分析。有些任务活动仅需要特定的几类资源就可以满足,因此必须对每一类资源中的人员的利用率进行分析。
3.2 人员数量时刻分布分析
人员数量时刻分布实质上是每时刻所用的人员的数量,对于时刻分布的分析能够直观的反映出人员在每时刻的使用情况。人员数量时间分布是考察工作安排的密集程度,评判方案安排是否人性化的一个重要指标[6]。系统熵的大小可以表示人员时刻分布偏离平衡态的程度,熵越小,偏离的程度越大。
根据熵的原理和定义,当系统可能处于m种状态,每种状态出现的概率为Pi(i= 1, 2,…,m)时,系统的熵为:
当系统的状态概率为等概率,即出现人员数量时刻分布均衡时,Pi=1/m(i= 1, 2,…,m)时,其熵达到最大[7]。
其中:m表示所用的总工期。
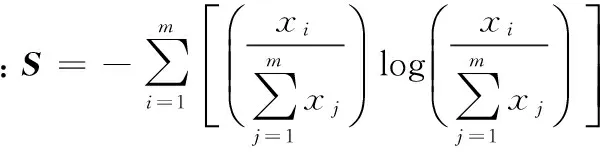
由熵的性质可知,Sx的取值范围在0~1,Sx越小,输入向量各分量越接近,越均衡。即每时刻所用的人员的数量越均衡。
本文提出的基于相对熵的均衡性评价映射模型如下:yx=(1-TSx)。其中:yx为输出评价,yx越大表示每时刻的输入越均衡; T为均衡性重要程度系数,T∈[0, 1],T越大,表示均衡性越重要,在实例分析中T取1;Sx为相对熵。
4 军用飞机任务保障规划方案效率实例分析
以军用飞机的再次出动实际的任务需求为例,对于给出的两种保障任务规划方案进行对比分析。
4.1 方案1的效率分析
4.1.1 人员利用效率分析
根据图2可以得出方案1每个人员的利用率如图3所示。

图2 方案1的任务保障规划甘特图

图3 方案1的人员利用率


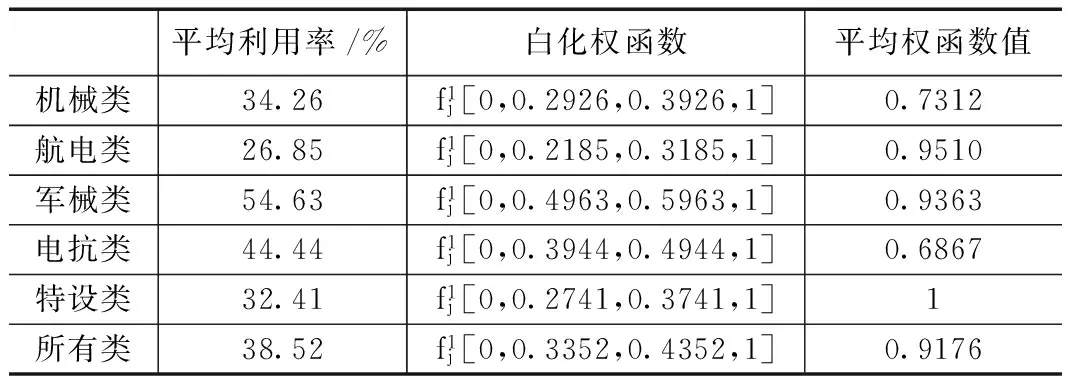
表2 方案1人员利用率计算表
如表2所示,对五类人员进行效率分析,取五类人员的平均权函数值,每类人员的权重为20%,则可以得到方案1每一类人员的平均效率为η11=(0.7312+0.9510+0.9363+0.6867+1)*0.2
=0.8610. 根据所有类中各类的利用率及每一类中人员的利用率对整个人员效率的重要性,并且结合专家经验,可给出所有类的权重为0.6,每一类人员的权重为0.4。由此可得出方案1的人员利用效率为yη1=0.6η12+0.4η11=0.8950。
4.1.2 人员数量时刻分布效率分析
根据图4.1 知,保障方案的总工期为27,系统有m=27种状态,Smax=log(27)=1.4313。方案1规范化的输入向量为X=(10,10,10,10,10,10,11,11,11,7,7,4,10,10,10,7,8,8,7,7,6,4,4,4,4,4,4,)系统熵为S1=1.4049,由相对熵公式可得Sx1=0.0184。人员数量时刻分布效率输出评价
yx1=(1-TSx1)=1-0.0184=0.9816。
4.1.3 方案1的效率分析计算
由给出的保障任务规划方案知所给出的方案的任务规划工期是最短,所以可以得到工期的效率为yT1=1。根据再次出动的实际需求及专家经验分配任务规划工期、各个人员的使用率、每时刻人员的数量分布的权重分别为0.5、0.3、0.2。依据构建的任务保障规划方案效率分析模型可得到方案1任务规划效率为:
y1=0.5yT1+0.3yη1+0.2yx1=0.964 8
4.2 方案2的效率分析
由图4可以得出表3所示的方案2的人员利用率计算表。
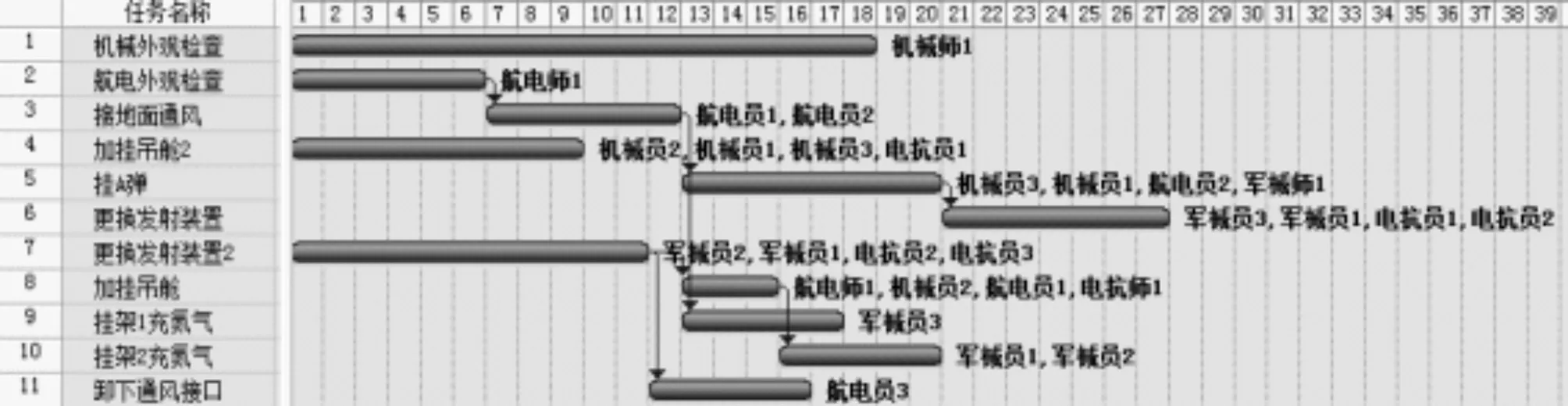
图4 方案2的任务保障规划甘特图
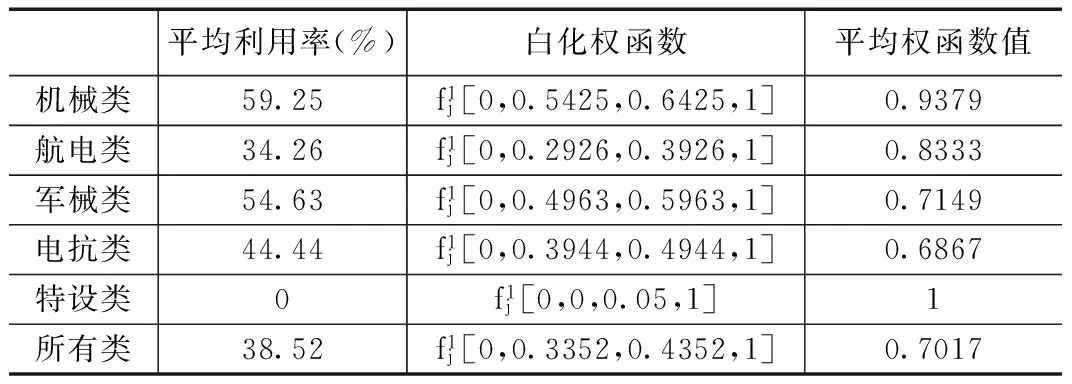
平均利用率(%)白化权函数平均权函数值机械类59.25f1j[0,0.5425,0.6425,1]0.9379航电类34.26f1j[0,0.2926,0.3926,1]0.8333军械类54.63f1j[0,0.4963,0.5963,1]0.7149电抗类44.44f1j[0,0.3944,0.4944,1]0.6867特设类0f1j[0,0,0.05,1]1所有类38.52f1j[0,0.3352,0.4352,1]0.7017
方案2每一类人员的平均利用效率为η21=(0.937 9+0.833 3+0.714 9+0.686 7+1)*0.2=0.834 6。类间与类内之间的权重分别为0.6、0.4。有方案2的人员利用效率为yη2=0.6η22+0.4η21=0.754 9。
方案2规范化的输入向量为X=(10,10,10,10,10,10,11,11,11,7,7,4,11,11,11,9,8,7,6,6,4,4,4,4,4,4,4,)。
Smax=log(27)=1.431 3,S2=1.400 2。
由相对熵公式可得Sx2=0.021 7。yx2=(1-TSx2)=1-0.021 7=0.978 3。
由给出的保障任务规划方案知所给出的方案都是工期最短的,所以可以得到工期的效率为yT2=1。根据再次出动的实际需求及专家经验分配任务规划工期、各个人员的使用率、每时刻人员的数量分布的权重分别为0.5、0.3、0.2。依据构建的任务保障规划方案效率分析模型可得到方案2任务规划效率为y2=0.5yT2+0.3yη2+0.2yx2=0.9221。
4.3 实例分析结果
综合任务规划工期、各个人员的使用率、每时刻人员的数量分布3个参数对效率分析的影响,对比方案1的任务规划效率y1=0.9648,方案2的任务规划效率y2=0.9221。可知方案1的保障规划更合理。
5 结论
提出了采用任务规划工期、人员利用率和人员数量时间分布3个保障方案评价参数,并对人员利用率及人员数量时间分布分别应用白化权函数和熵权法进行分析,并用实际案例对飞机再次出动保障方案评价进行了分析,最终通过对比得到了飞机再次出动最优保障方案,很好地完成了飞机再次出动保障方案效率分析。
研究结果表明,利用白化权函数和熵权法对选取的任务规划工期、人员利用率和人员数量时间分布3个评价参数进行分析可以得到很好的保障优化方案。能够在保障方案达到时间最优(即工期最短)的基础上,实现人员利用率较为平均,且在每时刻的人员数量较为均衡,使保障方案更加合理。
[1] 邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1992.
[2] Zhao D Y, Song H, A method of ameliorative multi-objective synthetic evaluation based on entropy weight and its application[J]. Journal of Ordnance Engineering College,2001,13(3):47-51.
[3] 邹志红,孙靖南等.模糊评价因子的熵权法赋权及其在水质评价中的应用[J].环境科学学报,2005,25(4):552-556.
[4] 苏 航. DEA交叉效率评价模型研究[D].吉林:吉林大学,2013.
[5] 刘思峰,谢乃明.基于改进三角白化权函数的灰评估新方法[J].系统工程学报,2011,26(2):244-250.
[6] 何逢标.综合评价方法MATLAB实现[M].北京:中国社会科学出版社,2010.
[7] 孙棣华,刘卫宁,宋 伟.基于相对熵的决策属性均衡性评价模型[J].系统工程理论与实践,2001,6:83-85.
Efficiency Analysis of Military Aircraft Mission Safeguard Plan
Cui Jianguo1,2, Xei Jianwen1, Yu Mingyue1,Xu Xiaoyu2,Wang Ruikai2
(1.School of Automation, Shenyang Aerospace University, Shenyang 110136, China;2.Shenyang Aircraft Design & Research Institute, Shenyang 110035, China)
Aiming at the problem that the efficiency analysis of the security task planning scheme of military aircraft is lack of effective method, the paper constructs a model of the efficiency analysis of the task support planning method based on the gray clustering algorithm and entropy weight method. In this model, using grey clustering method calculated and determined the effective parameters of Personnel utilization ratio of the security scheme. Subsequently, the distribution of personnel quantity time in the security scheme is calculated by the entropy weight method. On this basis, according to the task planning period, the personnel utilization ratio, time distribution of personnel the three parameters to ensure Task support planing scheme efficiency. In this paper, the efficiency of the model is verified by an example. The results indicate that the efficiency analysis model can effectively analyze military aircraft mission support plan, and has high reliability and good engineering application value.
efficiency analysis;gray clustering; entropy weight; whitening weight function; weight
2015-08-27;
2015-09-25。
航空科学基金(2010ZD54012;2007ZD54006);国防预研项目(A0520110023);国防基础科研项目(Z052012B002);辽宁省自然科学基金联合封闭基金(2014024003)。
崔建国(1963-),男,辽宁本溪人,博士后,教授,硕士生导师,主要从事飞行器综合健康管理方向的研究。
1671-4598(2016)06-0302-03
10.16526/j.cnki.11-4762/tp.2016.06.082
V267
A

