相控阵雷达接收系统噪声系数分析与测试验证

李维梅，刘 波，王旭艳

(西安空间无线电技术研究所,西安 710100)



相控阵雷达接收系统噪声系数分析与测试验证

李维梅，刘 波，王旭艳

(西安空间无线电技术研究所,西安 710100)

噪声系数是影响雷达接收机性能指标的主要参数之一，与雷达的作用距离紧密相关。文中采用将多端口网络转化为二端口网络的基本思想，对相控阵雷达接收系统的噪声特性以及增益进行了分析。首先，求出多端口网络的等效增益；再基于噪声系数的基本定义推出相控阵接收系统的噪声系数计算式；同时，基于等效的思想，提出了多端口网络噪声系数以及增益的直接测量方法；最后，用仿真以及实验验证了该计算及测量方法。

噪声系数；相控阵雷达；多端口网络

0 引 言

噪声系数作为影响雷达性能指标的重要参数之一，在雷达系统工程设计时必须进行优化设计和评估。对于微波雷达，从外部进入雷达接收机的噪声通常比较小。因此，噪声系数通常用来衡量其接收系统内部的噪声大小。相控阵天线在现代雷达中的应用越来越广泛[1-4]，如何准确地评估具有多通道的相控阵雷达接收系统的噪声系数[5]具有重要的工程意义。

关于相控阵雷达噪声系数的计算，文献[6]是对波束形成网络输出的总信号功率的表达式进行变换，根据其定义的等效天线增益，从总输出信号功率的表达式中得到等效接收系统的增益，进而根据等效噪声功率求出有源多通道系统的噪声系数。文献[7-8]在分析接收网络的噪声系数时，对于网络输出的总信号功率的表达式进行变换时，将增益分成了三部分：对信噪比没有影响的阵元增益、对噪声系数没有影响的网络接收增益，以及对信号有损耗的网络合成增益，进而得到系统的噪声系数。文献[7-8]对于输出信号功率表达式的变换采用了文献[6]的办法。文献[9]在求接收系统等效增益时也采用了文献[6]对输出的总信号功率表达式进行变换的办法，基于这种方法求出了双层波束合成网络的噪声系数。文献[10-13]则从多端口网络的角度对噪声系数进行了较详细的分析推导。文献[12-14]对噪声系数的测量进行了讨论，对比分析了n-1个输入端接负载且n个有源网络工作时的情况以及n-1个输入端接负载且只有1个有源网络工作的情况。文献[14]给出了在待测网络前接功分器的测试方法，其有源网络前以及有源二网络与合路器之间没有插损，只是考虑了功分器和合路器的固有插损，而对于某些实际的相控阵接收系统，为了波束形成的需要，有源二端口网络与合路器之间一般具有可变衰减器。文献[15]给出了阵列接收系统的输出信噪比，根据输出与输入噪声的功率比求得了系统的噪声系数。文献[16]在没考虑接收系统仪器附加噪声的情况下求得了噪声系数。

针对现有噪声系数的计算及测量方法，本文采用将多端口网络转化成二端口网络的办法，直接求得等效二端口网络的增益，再根据噪声系数的基本定义求得接收系统的噪声系数。在求解过程中，充分考虑了有源二端口网络前后的无源二端口网络引入的系统噪声。基于网络等效的思想，采用在接收网络前加功分器的办法，直接测量系统的噪声系数。为了说明本文所提方法的有效性，给出了一个四端口接收网络的仿真模型和测量实例。

1 噪声系数推导及特性分析

考虑一个相控阵接收系统的信号合成网络通用模型，如图1所示。网络的每一个接收通道包含了环行器、限幅器、低噪声放大器(LNA)、可调衰减器、数字移相器以及滤波器等。为了简化问题，对相控阵天线接收系统进行合并处理，因天线阵列单元接收到的远场回波信号是平面波，对于阵列天线，其每个阵列单元一般都具有相同的增益。因此，每个接收通道接收到的信号功率大小相等。通常所说的雷达接收机应不包括天线，所以可以将图1a)所示的系统简化为图1b)。将LNA前的损耗统称为输入损耗，用L1表示；LNA的噪声系数为NfA,增益为GA；LNA与合路器之间的固有损耗用L2表示，L2包括衰减器的固有插损、移相器的插损以及线损等。用L3m表示衰减器的控制衰减量，即波束形成时每个支路所加的可变衰减。合路器的固有插损用Ls表示。本文所有的损耗参数均认作为不小于1的参数，进行推导计算时取其真值。

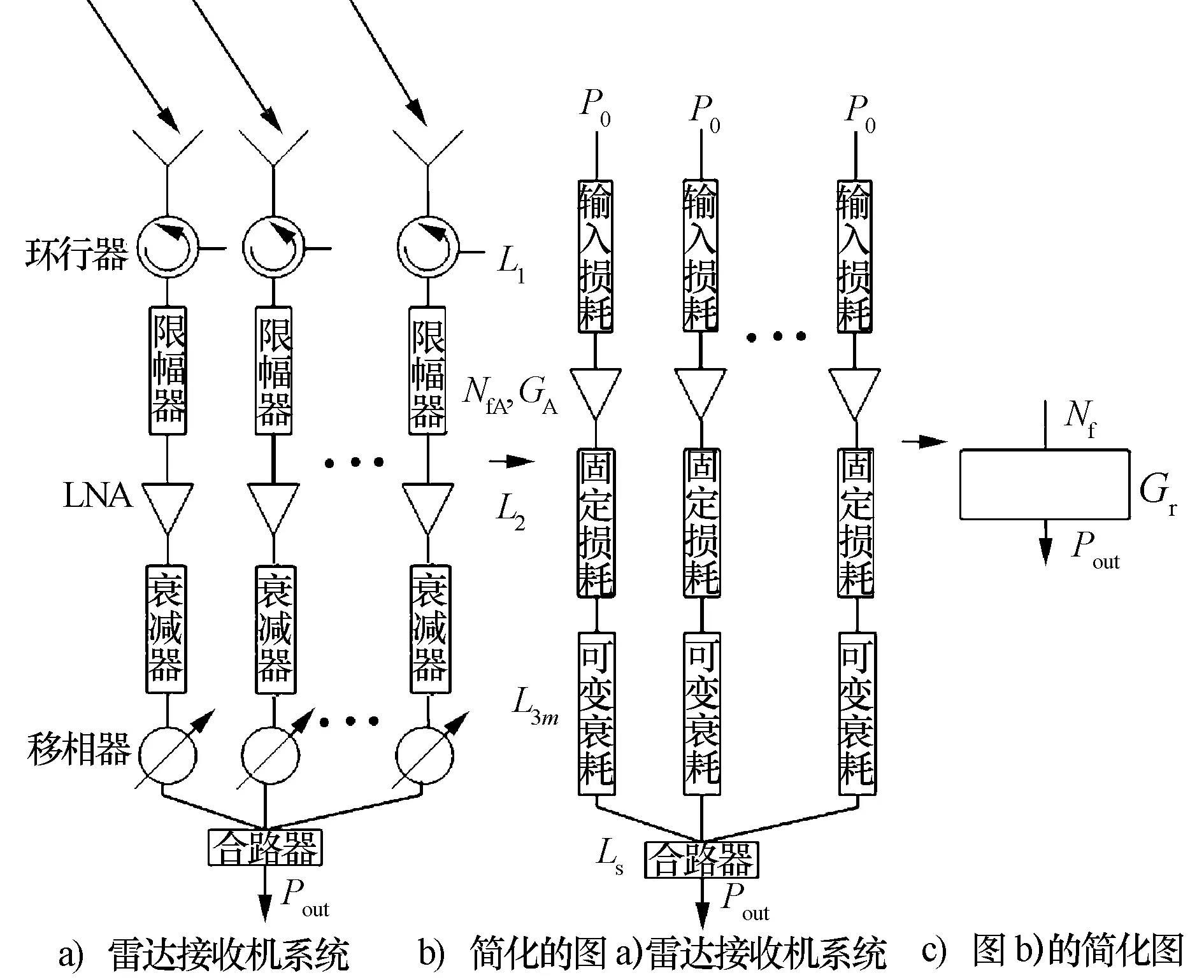
图1 相控阵雷达接收系统框图

基于噪声系数的原始定义，为了计算如图1b)所示接收系统这样的多端口网络的噪声系数，办法之一是将网络等效为一个二端口网络。根据相控阵的特点，入射到阵面的具有一定相位差的信号经过移相器的调整之后，到达合路器时是同相的，这里不考虑通道不一致性和相位加权等导致的相位误差。

噪声系数定义如下

(1)

式中：Sin为图1b)接收系统输入端总信号功率；Sout为接收系统输出端信号功率；Nin=kT0B为网络的输入噪声，对于多通道的接收系统，其单支路的输入噪声与整个接收系统的输入噪声是一样的[16]，其中，k为玻尔兹曼常数，B为工作带宽，T0为室温；Nout为接收系统输出端噪声功率；Gr为图1b)所示网络的等效接收增益。

假设系统有n条支路，则Sin=nP0，对于n路的合路器，其每个输入端口的信号功率只有1/n到达其输出端口。因此,第m条支路的信号到达合路器输出口的信号功率为

Som=P0Gm/(nLs)

(2)

式中：Gm为第m条支路的增益，有

Gm=GA/(L1·L2·L3m)

(3)

对于有用信号，加法器的输出为各支路信号功率转化成场叠加后再计算的总功率，因相控阵每一支路的信号经过移相器的作用到达合路器输入口时的相位相同，则合路器输出信号功率为

(4)

将式(2)和式(3)代入式(4)，进而可以求得该接收系统的等效增益为

(5)

根据式(1)，合路器前单个接收通道输出的噪声功率为

Nom=kT0B·Nfm·Gm

(6)

式(3)已经求得Gm，Nfm为单个接收支路的噪声系数，由多级接收系统的噪声系数级联公式可得

(7)

合路器自身的产生噪声功率如下

(8)

第m条接收通道经过合成网络产生的噪声功率到达合路器的输出口时为Nom/nLs，则合成网络总输出的噪声功率为

(9)

将式(5)、式(9)代入式(1)，得到接收系统的噪声系数为

(10)

至此，我们可以将图1b)所示的接收系统简化为图1c)，该二端口网络的增益为Gr,噪声系数为Nf。

2 噪声系数测量

通常噪声系数表征的是一个二端口网络的特性，对于噪声系数的直接测量，文献[13-14]提到在n-1个输入端接负载且n个有源网络工作时情况与n-1个输入端接负载且只有1个有源网络工作情况下进行测量，文中的分析均没有考虑有源二端口网络后接衰减器的情况。实际上，对于多端口网络的噪声分析，有源二端口网络和合路器之间的可变衰减量，对于系统输出的噪声有很大影响。因此，对于噪声系数的测量，将系统等效为一个二端口网络将会更加直观。根据上面的分析，可以将多端口合成网络等效成一个二端口网络，即可以将图1b)等效为图1c)的系统，其增益为Gr,噪声系数系数为Nf。既然可以将图1b)等效为图1c)，那么就可以在图1b)所示系统前端加一个功分器，将其变成图2a)的系统，即本文的测量系统。图1b)系统前加了功分器之后，其等效接收系统就变成图2b)的系统。为了和图1b)的信号形式保持一致，固有损耗里不再包含移相器的贡献，因为实际相控阵接收系统各支路不同相位的入射信号经过移相器的作用到达合路器输入口时是同相的。图1c)与图2b)的差别在于图2b)多了一个大小为Lg的固有插损。根据噪声系数的级联公式，图2b)系统的噪声系数为

(11)

因此，若要求图1b)系统与图2a)测量系统的噪声系数计算结果的差异(用分贝表示)在于功分器的欧姆损耗Lg，即前端接有功分器的测量系统的噪声系数要比实际相控阵雷达的噪声系数大LgdB。如果是理想功分器，即其欧姆损耗为Lg=0 dB,那么求图1b)与图2a)所示系统的噪声系数应该相等。

图2 等效测量系统

3 实验结果分析

以下为该接收系统的噪声系数计算和测量的仿真与实验验证，其中，ADS仿真实验如图3所示，实验测量系统如图4所示。

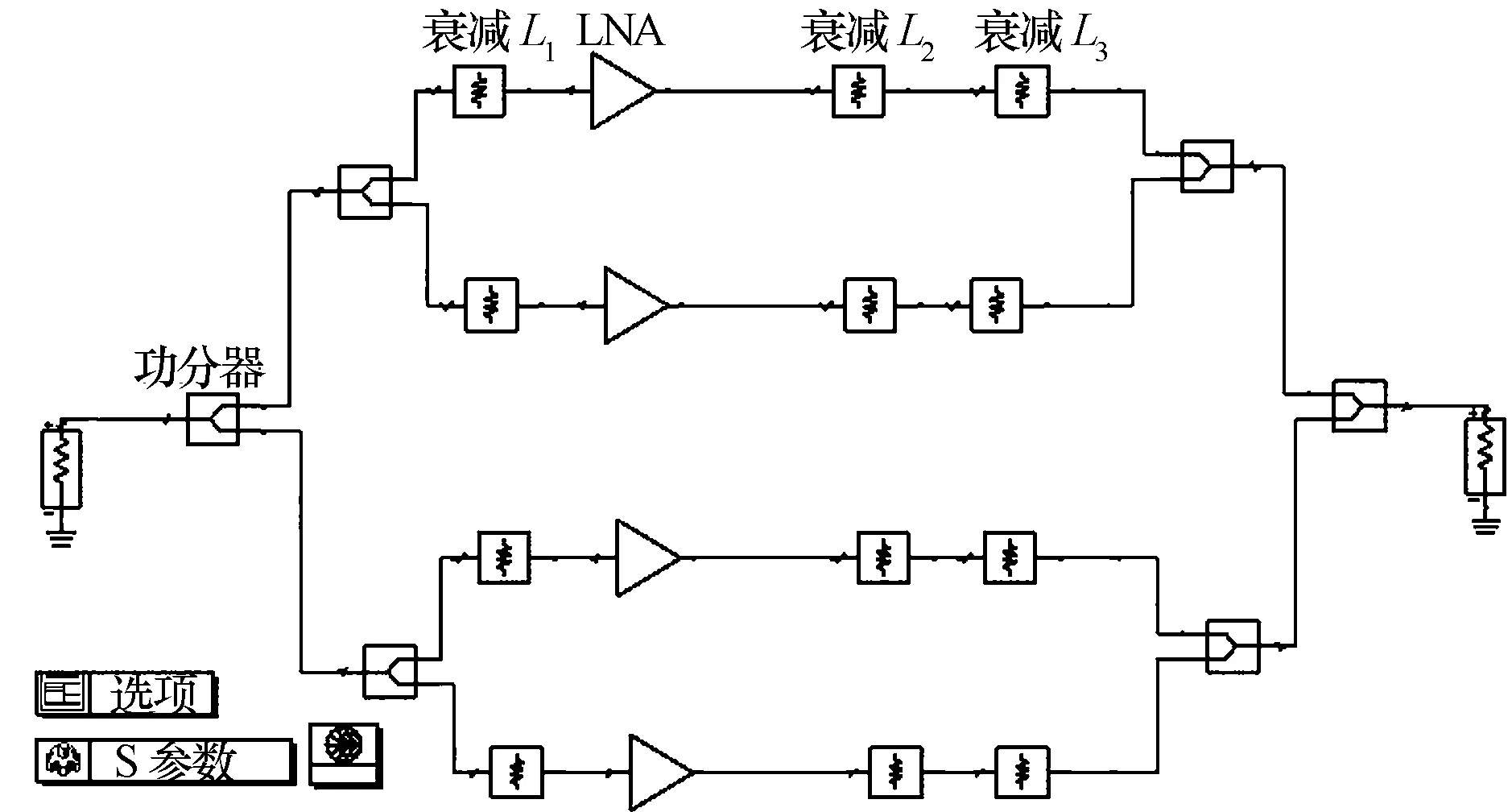
图3 实验ADS仿真框图

图4 实验测量系统

为了说明实验系统图2a)与实际接收系统图1b)的等效性，我们取Lg=0 dB，L1=0.9 dB，L2=8.3 dB，Ls=1 dB，GA=30 dB，NfA=1.4 dB，L3m取表1所示衰减量。将式(5)和式(10)计算得到的增益以及噪声系数与在ADS里仿真的结果进行比较。

表1 图2a)计算结果与图1b)(Lg=0)仿真结果对比dB

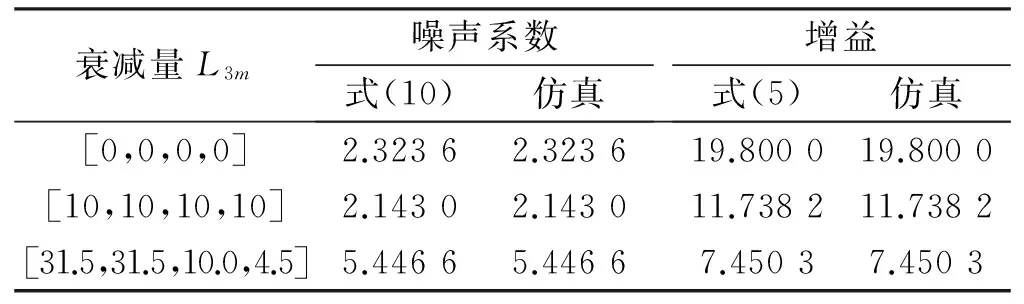
衰减量L3m噪声系数式(10)仿真增益式(5)仿真[0,0,0,0]2.32362.323619.800019.8000[10,10,10,10]2.14302.143011.738211.7382[31.5,31.5,10.0,4.5]5.44665.44667.45037.4503

从表1可以看出，当Lg=0 dB时，在衰减量为0(即不加衰减)，衰减量相同和不同情况下，实验系统图2a)与实际接收系统图1b)是完全等效的。为了进一步说明此结论，接下来取Lg=0.4 dB,即实验系统的功分器具有固有插损，实际上，也不可能将功分器做到完全没有固有插损，系统的其他参数不变。首先计算在L1=0.9 dB，L2=8.3 dB，Ls=1 dB，GA=30 dB，NfA=1.4 dB，L3m取表2所示衰减量时，实际接收系统图1b)的噪声系数与增益；然后，在ADS里仿真图2a)实验系统；最后，搭建实验系统进行测量。仿真原理图如图3所示。

在图3中，因为实际相控阵接收系统图1b)每条支路接收到的信号相位不同，经过移相器的调整之后，各支路信号到达合路器输入口时是同相的，在图2a)实验系统中，信号经过功分器之后是同相的，因为为了和图1b)保持一致，图2a)中不再需要移相器的作用，因此不含移相器。图4为实验测量系统,采用噪声系数测量仪直接进行二端口网络的测量。

表2 噪声系数计算图1b)与测量结果图2a) dB

衰减量L3m噪声系数计算仿真测量增益计算仿真测量[0,0,0,0]2.3242.7142.63～2.8419.80019.41519.25～19.54[10,10,10,10]2.5572.9472.81～3.119.8009.4159.30～9.52[31.5,31.5,10.0,4.5]5.4475.8375.65～5.927.4507.0656.98～7.21

对图1b)的计算以及对图2a)的仿真与测量结果如表2所示。从表2可以看出，噪声系数的仿真结果比计算结果大0.4 dB，而增益却比计算结果小0.4 dB，这是因为仿真系统前接有欧姆损耗为0.4 dB的功分器，而实际相控阵接收网络的噪声系数和增益计算是不含有功分器的。对于测量结果，基本与仿真结果吻合，但是也有些许差异，那是因为噪声系数测量仪测量时本身存在0.15 dB～0.2 dB的误差。由此，我们可以得出，本文对于噪声系数的计算与测量方法是可行的。

4 结束语

对于相控阵雷达接收系统，本文提出用等效的办法将多端口网络转化成一个二端口网络，求得网络的等效增益，再基于噪声系数的基本定义，考虑系统器件的附加噪声，进而求得多端口接收系统的噪声系数。同时提出用仿真和实验对相控阵接收系统进行等效验证测量的办法，仿真和实验结果表明本文所提出的噪声系数计算与测量方法是正确可行的。

[1] RYSZARD B,WOLFGANG H.Naval radar trends:A look back-a look forward[C]//2015 16th International Radar Symposium (IRS).Dresden:IEEE Press,2015:13-19.

[2] SGAMBATO P,BOTTA N,CELENTANO S,et al.System manager for AESA radar systems[C]//2015 IEEE National Radar Conference.Arlington,VA:IEEE Press,2015:1734-1738.

[3] KAWALEC A,KLEMBOWSKI W,WITCZAK A,et al.Military surveillance radars:from fixed to nonrotating antennas[C]//2015 16th International Radar Symposium (IRS).Dresden:IEEE Press,2015:967-972.

[4] PENG Z Y,RAN L X,LI C Z.A 24 GHz low-cost continuous beam steering phased array for indoor smart radar[C]//2015 IEEE 58th International Midwest Symposium on Circuits and Systems (MWSCAS).Fort Collins:IEEE Press,2015:1-4.

[5] YU H B.Noise characteristic analysis of multi-port network in active electrically scanned array radar[C]//2015 IEEE International Conference on Microwaves,Communications,Antennas and Electronic Systems (COMCAS).Tel-Aviv,Israel:IEEE Press,2015:1-4.

[6] 张光义.相控阵雷达系统[M].北京:国防工业出版社,1994.

ZHANG Guangyi.Phased array radar system[M].Beijing:National Defense Industry Press,1994.

[7] 栾铸微,王金锋.阵列接收噪声系数分析[J].雷达与对抗,2010,30(4):25-28．LUAN Zhuzheng,WANG Jinfeng.The analysis of noise factor of array receiver[J].Radar & Ecm,2010,30(4):25-28.

[8] 吉 胜.相控阵雷达接收系统噪声系数分析[J].现代电子技术,2013,36(1):21-24.

JI Sheng.Analysis of noise figure in phased array radar receiver system[J].Modern Electronic Technique,2013,36(1):21-24.

[9] 高 兵,杨丽丽.相控阵噪声系数特性及其典型应用分析[J].现代雷达,2014,36(4):14-18.

GAO Bing,YANG Lili.Noise factor characteristic analysis of phased array with its representative application[J].Modern Radar,2014,36(4):14-18.

[10] 赵旭昊.相控阵天线多通道并联噪声系数分析[J].现代雷达,2015,37(3):55-62.

ZHAO Xuhao.Noise figure analysis of parallel multi-channels in phased array antenna[J].Modern Radar,2015,37(3):55-62.

[11] 周求湛,王树勋,戴逸松.N级微波四端网络的噪声参数计算[J].计量学报,2004,25(1):70-75.

ZHOU Qiuzhan,WANG Shuxun,DAI Yisong.Noise parameters calculating for N-stage microwave two-port[J].Acta Metrologica Sinica,2004,25(1):70-75.

[12] 顾墨琳,林守远.有源相控阵接收系统的噪声测试[J].现代雷达,2004,26(3):54-57．

GU Molin,LIN Shouyuan.Noise temperature measurements of active phased array receiving system[J].Modern Radar,2004,26(3):54-57.

[13] 於洪标.相控阵雷达中多端口网络的噪声特性分析[J].微波学报,2009,25(2):58-61.

YU Hongbiao.Noise characteristic analysis of multi-port network in phased array radar[J].Journal of Microwaves,2009,25(2):58-61.

[14] 郭文刚,郗洪杰.阵列系统中多端口网络噪声系数测试分析[J].无线电工程,2011,41(3):59-61.

GUO Wengang,XI Hongjie.Noise figure test and analysis of multi-port network in array system[J].Radio Engeering,2011,41(3):59-61.

[15] LEE J J.G/T and noise figure of active array antennas[J].IEEE Transactions on Antennas and Propagation,1993,41(2):241-244.

[16] GATTI R V,DIONIGI M,SORRENTINO R.Computation of gain,noise figure,and third-order intercept of active array antennas[J].IEEE Transaction on Antennas and Propagation,2004,52(11):3139-3142.

李维梅 女，1986年生，博士。研究方向为GEO SAR射频收发系统关键技术。

刘 波 男，1963年生，研究员，博士生导师。研究方向为卫星有效载荷系统。

王旭艳 女，1979年生，博士。研究方向为合成孔径声纳信号处理。

Analysis and Measurement of Noise Figure in Phased Array Radar Receiving System

LI Weimei，LIU Bo，WANG Xuyan

(Xi′an Institute of Space Radio Technology,Xi′an 710100,China)

As one of the key parameters affecting the performance indexes of the radar receiving system,noise figure is closely related to the radar detection range.With the theory of equivalent conversion of a multi-port network model into a two-port network model,noise characteristic and gain of the phased array radar receiving system is analyzed and measured.Firstly,the equivalent gain of the multi-port network is computed by the equivalent theory.Then,based on the original definition of the noise figure,the formula of noise figure is deduced.At the same time,based on the equivalent theory,a direct measurement method of the noise and gain is presented.Finally,the method of computing and measuring noise figure and gain is verified by simulation and experiment.

noise figure; phased array radar; multi-port network

发技术·

10.16592/j.cnki.1004-7859.2016.10.016

李维梅 Email：li_weimei@163.com

2016-07-20

2016-09-20

TN958.92

A

1004-7859(2016)10-0069-05