一种新的多目标融合关联算法
孙伟 尚金涛 朱鲲
(声纳技术重点实验室 第七一五研究所,杭州,310023)
一种新的多目标融合关联算法
孙伟 尚金涛 朱鲲
(声纳技术重点实验室 第七一五研究所,杭州,310023)
多目标关联是多阵多传感器声呐数据融合的前提和关键,结合灰色理论利用多种量测信息,提出了一种新的多目标融合关联算法。利用目标方位、LOFAR和DEMON谱特征线谱实现多目标的融合关联,取得了更好的关联结果,通过仿真验证了所提算法的关联性能,相较纯方位关联算法有提高。
声呐数据处理;灰色理论;线谱;多目标关联
1 引言
目前,网络信息战是现代战争的趋势,而多传感器融合技术是其关键。多传感器融合技术利用了不同类型的多个传感器,具有较好的鲁棒性,可以有效扩展时间、空间覆盖能力及减小系统的模糊性程度。因具有如此多的优点,它在水声领域也有着广泛应用,如分布式节点探测、舰艇多阵联合观测等。
如何判断来自于不同传感器或两个不同声呐基阵的两条航迹是否代表同一个目标,目前主要有两类算法:一类是基于统计的方法,另一类是基于模糊数学的方法。统计方法的思想是将航迹关联问题转换为假设检验问题,构造利用两局部节点的航迹估计服从特定分布的检验统计量,并根据事先确定的门限值来判断两航迹是否来自同一目标。当系统包含有较大的导航、传感器校准及转换和延迟误差时,统计方法会显得力不从心。由于航迹关联判决中存在着较大的模糊性,而这种模糊性可以用模糊数学的隶属度函数来表示,也就是用隶属度概念来描述两个航迹的相似程度。然而基于统计的航迹关联方法需要假设典型的分布规律,运用模糊数学方法时隶属函数也需要主观给定。
采用灰色理论对多目标多传感器航迹关联进行研究,根据数据列因素之间发展态势的相似或相异程度来衡量航迹间接近的程度,对样本量的大小没有太高要求,分析时也不需要典型的分布规律。本文结合灰色理论提出一种利用目标已有的特征信息如方位、LOFAR、DEMON线谱等特征进行多目标的融合关联,为航迹关联问题探索一条新的途径。
2 算法原理
2.1 关联数据的预处理
目前声呐基阵直接或间接获得可以关联的信息包括方位、LOFAR谱、DEMON谱等,对以上信息进行标准化,归一化运算后求得关联系数,进而得到关联度。
2.1.1 数据序列的确定
选取基阵A的跟踪目标i为参考目标,包括方位、LOFAR谱中的线谱条数及对应的具体频率位置、DEMON谱中的线谱条数及对应的具体频率位置等信息,记为。设来自基阵B的第j个目标为比较目标,记为,假设基阵B共有n2个目标进行比较,其每个目标所含的特征信息种类与参考目标相同。
2.1.2 数据的标准化
为了保证数据具有可比性,在进行灰关联分析时,需要对每个目标的每种特征信息进行重新生成处理。这里采用区间值化的方法对特征指标数据进行标准化处理。
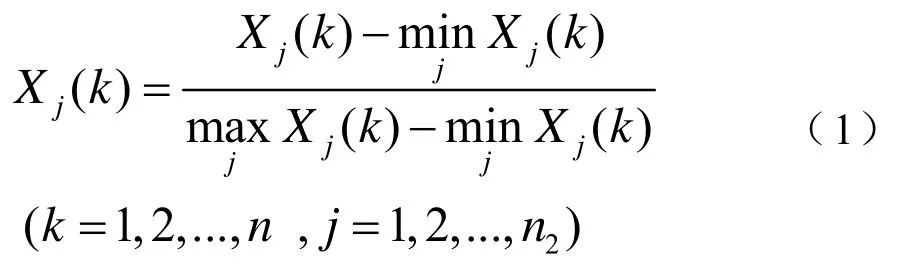
2.1.3 计算灰关联系数

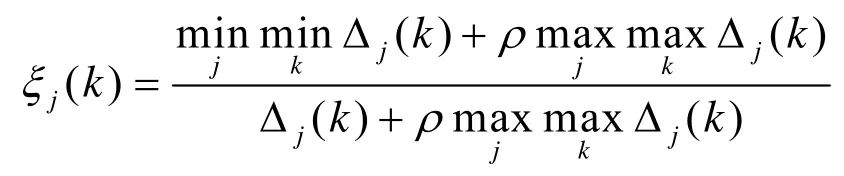
其中ρ为分辨系数,ρ越小,分辨力越大,一般取ρ=0.5,ρ的具体取值可视具体情况而定。称为两级最小差,为两级最大差,称为第k个指标X0与Xj的绝对差。于是可以求出的关联:
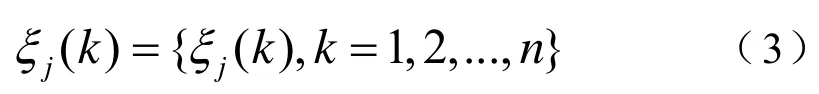
2.1.4 计算灰关联
将每一比较序列各个指标的关联系数集中体现在一个值上(便于比较),这个值称为灰关联度。比较序列Xj对参考序列的灰关联度常记为:
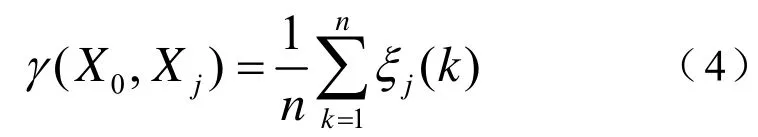
采用平均值法计算灰关联度实际上是认为比较序列的各个指标对于关联分析是同等重要,即作平权处理。但事实上,这些因素对关联判决的影响是不同的,因而必须进行加权处理。令表示相应指标的权系数,且,则可以定义加权关联度为:。
2.2 灰关联航迹关联准则
当计算出描述航迹接近程度的灰关联度之后,下一步就是如何判决两航迹间的相似性。为了给出航迹与航迹间的相似性判决,需要对关联度按从大到小进行排序,即得灰关联序列。这里我们采用最大关联度识别原则,即

则判决航迹i在l时刻与航迹j*关联,并且j*在 l时刻不再与其他航迹关联;否则来自局部节点的航迹i在l时刻不与来自局部节点2的任何一条航迹关联。其中ε为阈值参数,0.5≤ε≤1,阈值可以通过仿真来确定。
为了控制航迹关联检验的完结与终止,可进一步引入航迹关联质量。若在l时刻判决航迹与航迹为关联对,则

3 仿真验证
仿真一给出两基阵各目标方位相似性较差的条件下基于纯方位多目标关联算法的关联效果。仿真二给出的是两基阵各目标方位相似性较差的条件下联合多维特征信息的多目标关联算法的关联效果。
仿真条件:基阵A坐标(0 m,0 m);基阵B坐标(-600 m,400 m);目标1初始坐标(200 m,900 m),航向90°,航速-5 m/s,方位测量误差1°。目标2初始坐标(-100 m,1 000 m),航向60°,航速2 m/s,方位测量误差1°。目标3初始坐标(500 m,1 000 m),航向270°,航速-4 m/s,方位测量误差1°。观测时长为300 s。基阵A所测得的目标1、2、3分别与基阵B所测得的目标1、2、3对应。目标1~3对应的LOFAR谱线谱序列分别为(30,45,60,90)Hz、(45,60,100,130)Hz、(48,110,150,230)Hz,目标1~3对应的DEMON谱基频频率分别为7 Hz、13 Hz、9 Hz。
图1给出的是两基阵的方位历程图,图2(a)给出的是两基阵对不同目标的LOFAR谱分析结果。图2(b)给出的是两基阵对不同目标的DEMON谱分析结果。从图中可以得到目标间LOFAR谱和DEMON谱的相似度信息,利用这些频谱信息可以用来进行多目标之间的关联。
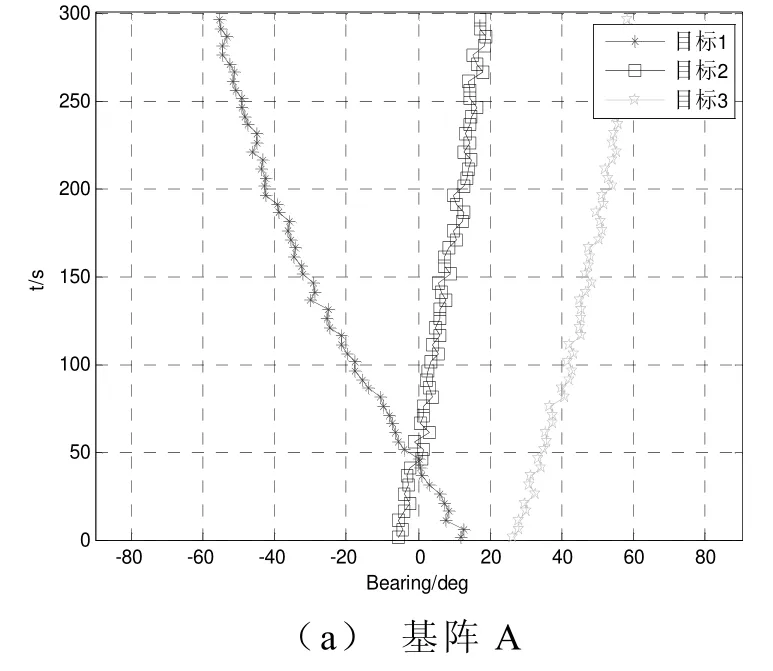
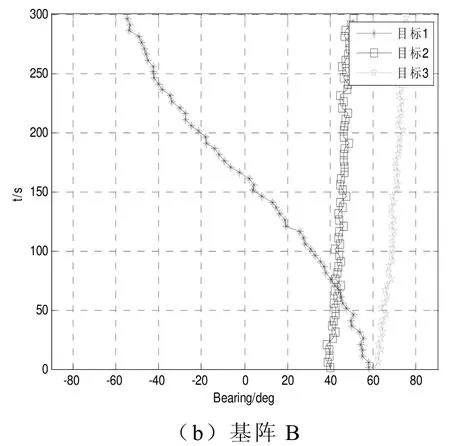
图1 两基阵的方位历程图
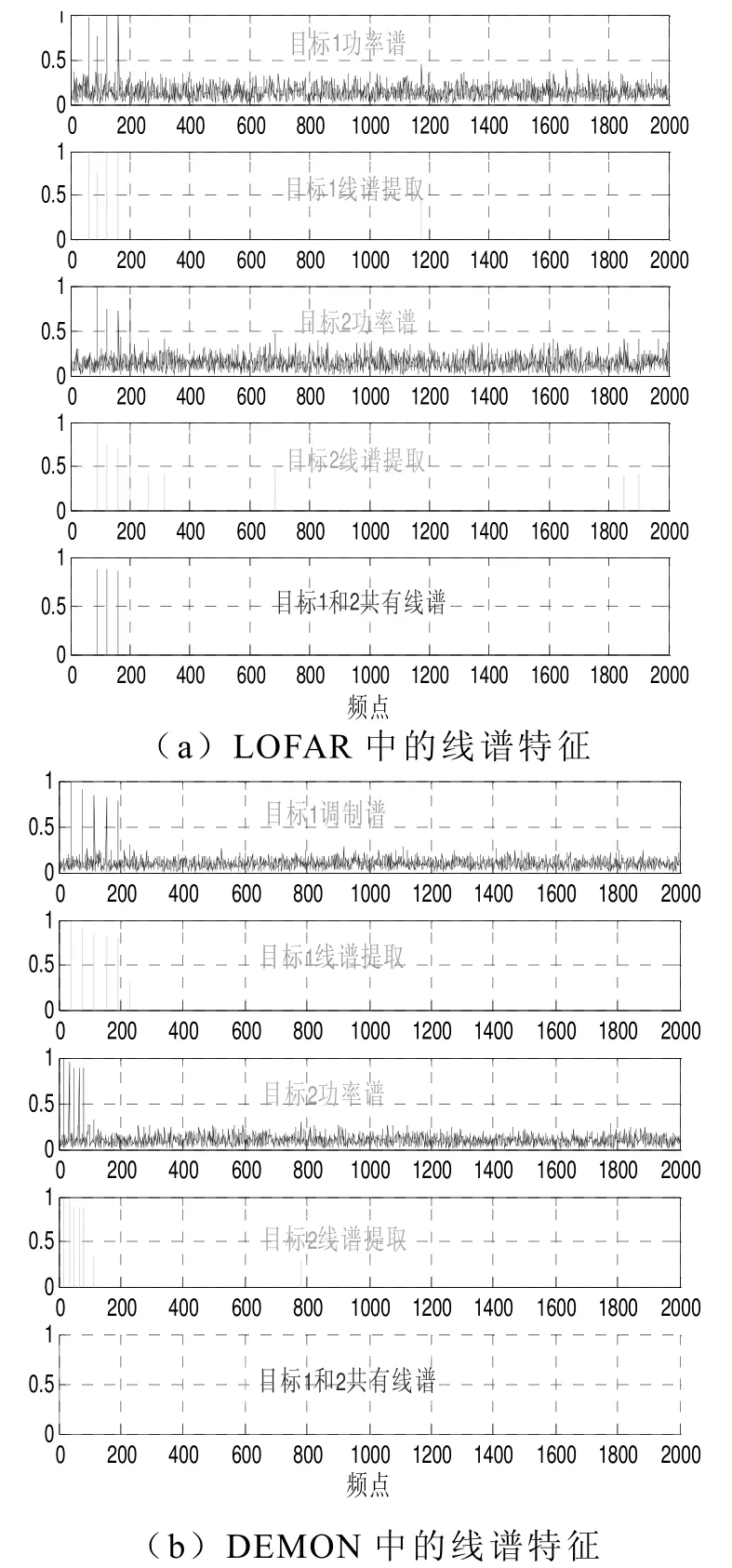
图2 比较两目标的LOFAR和DEMON中线谱特征
表1给出的是基于纯方位多目标关联算法的关联系数,表2给出的是联合多维特征信息的关联算法的关联系数。由表1可知,基于纯方位多目标关联算法在两基阵目标方位相似度较低条件下,效果并不理想。由表2可知,联合多维特征信息的关联算法在两基阵目标方位相似度较低条件下,关联性能仍然较高。
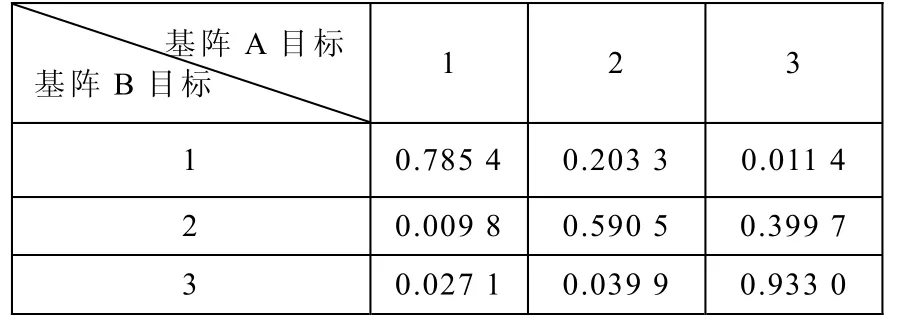
表2 联合多维特征信息的关联算法的关联系数
4 结束语
本文提出一种新的利用方位、LOFAR谱,DEMON谱等多维特征解决目标关联问题的算法,并详细介绍该算法的原理及步骤。通过仿真数据验证该算法在目标观测方位相似度较差的情况下,仍具有较好的关联性能,具有一定的工程应用价值。
[1]WANG GUOHONG,HE YOU.Improved association of ESM measurments with radar tracks[C].IEE Inter.Conf.on Radar,Edingburgh,UK,1997:648-652.
[2]LIU F,CAI X J,SHI B,et al.Multisensor data fusion based on genetic algorithm[C].1996,SPIE,1898:43-48.
[3]何友,彭应宁.一种新的多目标多传感器航迹相关算法[J].清华大学学报,1997,9:108-113.
[4]郭文艳,韩崇昭,雷明.基于EMD和灰关联技术的航迹关联方法[J].控制与决策,2008,23(7):803-807.
[5]刘源,谢维信,杜文吉,等.基于多传感器多目标特征信息的模糊数据关联算法[J].系统工程与电子技术,1998,12:18-23.

