平原水网区雨水管渠设计研究——以苏州市城市中心区为例

陆敏博，钱海平

（悉地（苏州）勘察设计顾问有限公司，江苏 苏州 215123）

平原水网区雨水管渠设计研究
——以苏州市城市中心区为例

陆敏博，钱海平

（悉地（苏州）勘察设计顾问有限公司，江苏 苏州 215123）

以苏州市城市中心区为例，分析了平原水网区排水防涝的特点，进行了恒定均匀流推理公式法和数学模型法两种雨水管渠设计方法的适用性分析，通过数学模型法得出与城市内涝防治设计重现期相匹配的雨水管渠设计重现期。

平原水网区；雨水管渠设计重现期；内涝防治设计重现期；数学模型法

0　引　言

雨水管渠设计方法体现了设计的科学性和合理性，设计重现期体现了城市抵御内涝灾害的能力，两者之间也关系到雨水管渠的工程投资。合理选用雨水管渠设计方法和确定设计重现期，是当前城市排水防涝工作面临的重要课题[1]。

苏州市城市中心区设立防洪包围圈，总面积89.26 km2。包围圈西面以黄花泾、京杭大运河为界，东面以苏嘉杭高速公路为界，南面以京杭大运河为界，北面以西塘河、沪宁高速公路为界，如图1所示。本文以苏州市城市中心区为例，分析了平原水网区排水防涝的特点，进行了恒定均匀流推理公式法和数学模型法两种雨水管渠设计方法的适用性分析，最后通过数学模型法，得出与城市内涝防治设计重现期相匹配的雨水管渠设计重现期。

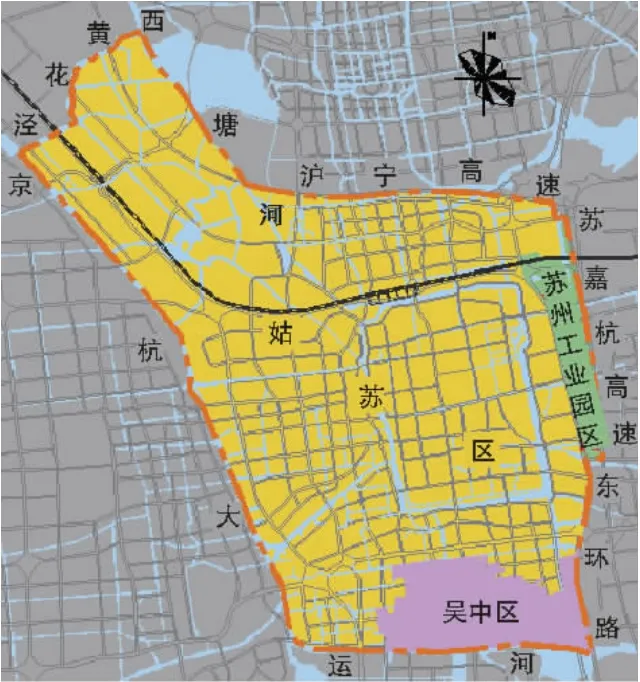
图1　苏州市城市中心区范围示意图

1　平原水网区排水防涝特点

平原水网区水系发达、地势低平，因而河流比降小，致使水流平缓、迂回。苏州市城市中心区雨水排水系统采用自排为主，机排为辅的排水模式。包围圈内水系周边地块降雨径流基本上就近、分散、自流直接排入内河水系；市政道路及距离河道较远地块的降雨径流经雨水管渠收集后就近排入内河水系；部分低洼地在雨水管渠末端设置强排至周边管渠或水系。包围圈内的涝水通过排涝泵站抽排至外河水系。

由于雨水管渠出水口普遍采用淹没出流，所以实际排水能力受内河水系水位的制约显著，而内河水系水位则由排涝泵站控制。若遇超标暴雨，且排涝泵站能力不足，雨水管渠就来不及排除降雨径流，地面积水甚至内涝就产生了。雨水管渠系统是城市排水防涝体系中最重要的部分之一，因此，雨水管渠设计重现期需要和城市内涝防治设计重现期相匹配。

平原水网区的排水防涝体系显著特点之一是单个雨水口的汇水区面积较小。以苏州市城市中心区为例，内河水系的间距一般不超过2 km，雨水管渠就近排入内河水系，其长度一般不超过1 km，整个苏州市城市中心区约1 500个雨水汇水区，每个雨水口的汇水区面积一般在5～15 hm2，最大的汇水区面积不足30 hm2。

2　雨水管渠设计方法选用

目前，雨水管渠设计常用的方法有恒定均匀流推理公式法和数学模型法两种。推理公式法适用于较小规模排水系统的计算，当应用于较大规模排水系统的计算时会产生较大误差。美国一些城市规定的推理公式适用范围分别为：奥斯汀4 km2，芝加哥0.8 km2，纽约1.6 km2，丹佛6.4 km2且汇流时间小于10 min；欧盟的排水设计规范要求当排水系统面积大于2 km2或汇流时间大于15 min时，应采用非恒定流模拟进行城市雨水管网水力计算[2]。我国现行《室外排水设计规范》（GB 50014—2006，2014年版）提出当汇水面积超过2 km2时，雨水设计流量宜采用数学模型进行确定。

由于苏州市城市中心区的每个雨水口的汇水区面积远小于2 km2，因此苏州市城市中心区雨水管渠设计建议采用恒定均匀流推理公式法进行。

排水工程设计常用的数学模型一般由降雨模型、产流模型、汇流模型、管网水动力模型等一系列模型组成，涵盖了排水系统的多个环节[2]。数学模型可以更加准确地反映雨水管渠系统与地表收纳水体之间的相互关系，当对已建雨水管渠系统所处区域的下垫面、河网水系、地形高程、管道布置、管道参数等资料掌握充分的情况下，可以采用数学模型法进行复核。

3　雨水管渠设计重现期的选用

3.1典型汇水区及推理公式法设计

选取苏州市城市中心区典型汇水区10 hm2为例，具体形态详见图2。

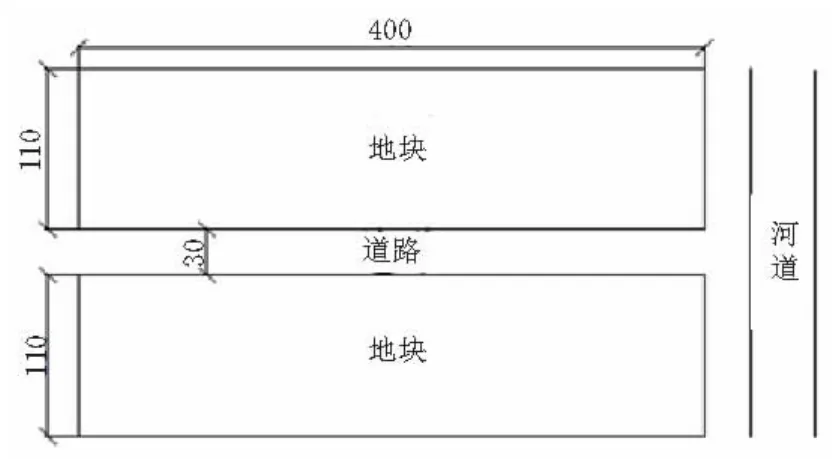
图2　典型汇水区示意图

相关参数如下：道路设计标高4.4～4.9 m（吴淞高程，下同），纵坡0.3%；管道设计标准采用苏州暴雨强度公式3 a一遇2 h雨量，综合径流系数按照新建地区不超过0.5的标准取0.5，最小覆土1.5 m。按照推理公式法进行雨水管渠设计，管径-坡度为d600-1.2‰～d1 350-0.7‰，设计道路和管道情况见图3。

3.2数学模型法复核

2015年3月苏州市人民政府在江苏省率先出台《苏州市城市中心区排水（雨水）防涝规划》。利用该规划中所建立的InfoWorks ICM数学模型和设计雨型，对典型汇水区设计方案进行长历时24 h 50 a一遇设计降雨雨型复核。

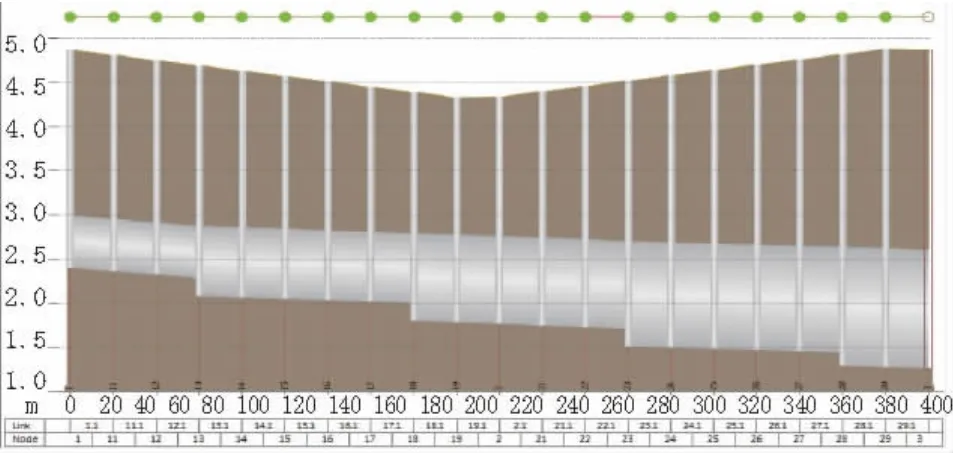
图3　设计道路及管道方案

复核分析设计了两个方案，方案1不考虑管道沉积，方案2根据目前养护标准设定沉积率。复核采用的综合径流系数采用偏不利值0.8，下游河道水位按照苏州城市中心区最高排涝控制水位3.4 m（水位淹没出水口管顶以上0.8 m）取值。复核方案详见表1。

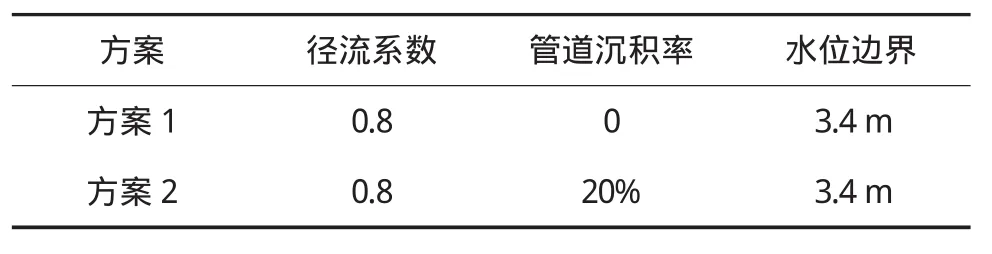
表1　长历时大重现期降雨雨型复核方案

方案1模拟结果表明，管网呈压力流状态，但地面不积水（见图4）。分析原因，主要是实际管网内的压力流态和设计时的满管无压流态的排水能力差别引起。当管道形成压力流时，其排水能力依然可以按照曼宁公式计算，只是此时坡度不再是管道的敷设坡度，而应该是其实际的水力坡度。如图中的末端管，设计管径d1 350，设计坡度0.7‰，而此时水力坡度为2‰，管道过流能力提升61%，达到2 276.7 L/s。另一方面，管道设计时，最低点也有1.5 m的覆土厚度，这无形中又为管道的水力坡度提供了一定的增长空间，从而造成3 a一遇设计管道50 a一遇降雨地面亦不积水。尽管此时地面不积水，但管道处于压力流状态，随着水力坡度的增大，管道所承受的压力也随之增大，长此以往不利于管道维护，安全系数也很低。

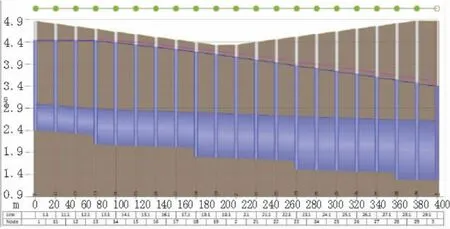
图4　方案1复核结果

方案2模拟结果表明，地面会产生积水，但最大积水深度为11 cm（见图5），未超过内涝防治标准定义的15 cm限值。分析其原因，主要是管网实际运行过程中发生的淤积现象，一方面减小了管道过流能力，另一方面加大管道糙率。过流断面的缩小，水力坡度增长的更快，造成了管网部分检查井冒溢。

TU992

B

1009-7716（2016）04-0111-02

10.16799/j.cnki.csdqyfh.2016.04.034

2015-12-11

陆敏博（1982-），男，江苏张家港人，硕士，工程师，从事给排水工程和综合管廊工程的规划设计工作。