基于不确定寿命的不可修冷贮备系统可靠性分析

刘 颖，马 瑶，王 林

（天津科技大学计算机科学与信息工程学院，天津 300222）

基于不确定寿命的不可修冷贮备系统可靠性分析

刘 颖，马 瑶，王 林

（天津科技大学计算机科学与信息工程学院，天津 300222）

针对无大量样本存在的不可修冷贮备系统，假设各部件寿命为相互独立的非负不确定变量，建立了3类不可修冷贮备系统可靠性的基本数学模型，即转换开关完全可靠情形的不可修冷贮备系统、开关寿命0-1型的不可修冷贮备系统以及开关寿命连续型的不可修冷贮备系统.分别对这3类不可修冷贮备系统进行可靠性分析，给出此3类冷贮备系统可靠度及平均寿命的具体数学表达式，并给出了数值算例.

不确定理论；不可修系统；可靠度；平均寿命；冷贮备系统

系统可靠性理论是20世纪40年代发展起来的一门综合性的基础理论，它是以系统的寿命特征为主要研究对象的.在传统可靠性理论［1-4］的研究中，系统的寿命通常被视为一个非负的随机变量，主要应用概率论为主要数学工具来研究系统的寿命特征.尽管传统可靠性理论在许多情况下被证明是有效的，但是使用概率论来处理可靠性问题必须满足3个基本前提：事件需明确定义；有大量样本空间存在；样本之间具有概率重复性.当样本量足够大时，概率分布可能足够接近的累积频率，在此情况下，可使用概率论解决问题.当没有充足的样本数据时，则需要采用专家的主观信度，此时不确定性分布通常偏离累积频率，用概率论来处理可靠性问题就有一定的局限性，而不确定理论为解决此类问题提供了有效的办法.

刘宝碇教授于2007年提出了不确定理论［5］.不确定理论是处理不确定现象的一套公理化数学体系.近年来，不确定理论在很多领域都得到广泛应用，如投资组合选择问题［6］、设施选址问题［7］、最优分配问题［8］、最大流问题［9］、交通问题［10］、系统可靠性问题［11］等.

在系统可靠性领域中，对不可修冷贮备系统可靠性的分析是一个研究热点.近年来，学者们运用不同的数学工具分析了各种不可修冷贮备系统.如文献［3］将系统和各部件的寿命视为随机变量，对各类不可修冷贮备系统的可靠性进行了分析；文献［12］将系统的寿命看作模糊变量，建立了开关绝对可靠的不可修冷贮备系统可靠性的基本模型，并给出其可靠度和平均寿命的具体表达式；对于随机性和模糊性并存的不可修冷贮备系统，文献［13］将各部件的寿命看作相互独立的随机模糊变量，分别建立了转换开关不完全可靠情况下的几类不可修冷贮备系统基本模型，并对其可靠性进行了分析.目前，使用不确定理论作为主要数学工具来研究不可修冷贮备系统的文献较少.因此，本文将不可修冷贮备系统的各部件寿命视为不确定变量，建立可靠性的数学模型，分别给出系统可靠度和平均寿命的数学表达式及数值算例.

1 不确定理论基础知识

文献［5］中首先提出了不确定理论，又在文献［14］中对其进行了细化和补充.下面给出本文用到的相关定义和定理.

设Γ为非空集合，L是由Γ中的子集所构成的σ代数.L中的元素称为事件.为了介绍不确定理论的公理化定义，对任一不确定事件Λ，规定一个非负数值M｛Λ｝表示事件Λ发生的信度，其中信度M需要满足如下4条公理：

公理1（规范性） 对全集Γ，有M｛ Γ｝=1.

公理2（单调性） 对任意事件Λ1⊂Λ2，有M｛Λ1｝≤M｛Λ2｝.

公理3（自对偶性） 对于任一事件Λ和其对立事件Λc，有M｛Λ｝+M｛Λc｝=1.

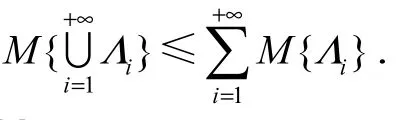
定义1［5］若集函数M：L→［0，1］满足以上四条公理，则称M为非空集合Γ上的不确定测度.

定义2［5］设Γ为非空集合，L是由Γ的子集构成的σ代数，M为Γ上的不确定测度，则称三元组（Γ，L， M）为不确定空间.

定义3［5］不确定变量定义为从不确定空间（Γ，L， M）到实数集的可测函数ξ，即对于任意Borel集B，集合｛γ∈Γ| ξ｛ γ｝∈B｝∈L 为一个事件.

定义4［5］若M｛ξ＜0｝=0成立，则称ξ为（Γ，L， M）上的非负不确定变量.

定义5［5］若f为实值可测函数，ξ1，ξ2，…，ξn为（Γ，L， M）上的不确定变量，则ξ=f （ξ1， ξ2，…，ξn）也为不确定变量，定义为函数ξ（ γ）=f （ξ1（ γ），ξ2（ γ），…，ξn（ γ）），∀γ∈Γ.

定义6［5］若ξ为Γ上的不确定变量.对于∀x∈R，若满足Φ（x）=M｛ξ≤x｝ ，则称Φ为ξ的不确定分布.

定义7［5］若不确定变量ξ的不确定分布函数为

其中a，b都为实数，且a＜b，则称ξ为线性的，记作ξ～L（ a， b）.

定义8［5］若不确定变量ξ的不确定分布函数为

其中a，b，c都为实数，且a＜b＜c，则称ξ为之字形的，记作ξ～Z（ a， b， c）.

定义9［5］若ξ为一个不确定变量，M为不确定测度，那么ξ的期望值定义为

只要以上两个积分中至少有一个是有限的.

定理2［14］若不确定变量ξ1和ξ2相互独立，分别服从线性分布：ξ1～L（ a1， b1）和ξ2～L（ a2， b2），则它们的和也服从线性分布，即

定理3［14］若不确定变量ξ1和ξ2相互独立，分别服从之字形分布ξ1～Z（ a1， b1， c1）和ξ2～Z（ a2， b2， c2），则它们的和也服从之字形分布，即

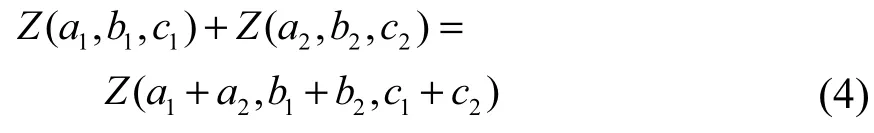
2 转换开关完全可靠的情形

所谓冷贮备系统是指贮备的部件既不失效也不劣化，贮备期的长短对以后使用时的工作寿命没有影响.假设系统由n个部件组成，在初始时刻，一个部件开始工作，其余n-1个部件做冷贮备.当工作部件失效时，贮备部件逐个去替换，直到所有部件都失效时，系统就失效.假设这n个部件的寿命分别为X1， X2，…，Xn，且它们相互独立.

例1 若冷贮备系统由3个部件X1， X2，X3构成，且X1～L（1.2，1.5）， X2～L（1.3，1.6）， X3～L（1.2，1.4），由式（3）可知X1+X2+X3～L（3.7，4.5），由式（1）可知其分布函数为

因此，该冷贮备系统的可靠度为

平均寿命为

例2若冷贮备系统由3个部件X1， X2，X3构成，而X1～Z（1.2，1.4，1.5），X2～Z（1.3，1.4，1.5），X3～Z（1.2，1.3，1.4），则由式（4）可知X1+X2+X3～Z （3.7，4.1，4.4），由式（2）可知其分布函数为

因此，该冷贮备系统的可靠度为

平均寿命为

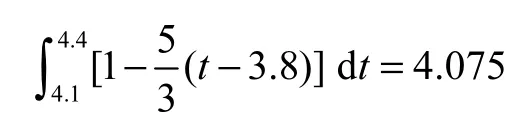
3 转换开关不完全可靠的情形

3.1 开关寿命0-1型

这里假设转换开关不完全可靠，其寿命是0-1型的不确定变量，即每次使用开关时，开关正常的信用度是p，开关失效的信用度是1-p.在以下两种情况下系统就失效：

（1）当正在工作的部件失效，使用转换开关时开关失效，这时系统会失效.

（2）所有n-1次使用开关时，开关都正常，在这种情形下，n个部件都失效时系统失效.

为求得系统可靠度，引入一个不确定变量

因此，该冷贮备系统的寿命为X= X1+X2+…+Xv.可求得

故系统可靠度为

平均寿命为

例3 该冷贮备系统由3个部件X1， X2，X3构成且X1～L（1.2，1.5），X2～L（1.3，1.6），X3～L（1.2，1.4），每次使用开关时，开关正常的信用度为0.8，由式（3）可知X1+X2～L（2.5，3.1），X1+X2+X3～L（3.7，4.5），首先计算

此外有M｛ v=1｝=0.2，M｛ v=2｝=0.2，M｛ v=3｝=0.8.因此，可以得到

因此该冷贮备系统的可靠度为

平均寿命为

3.2 开关寿命连续型

假定开关的寿命XK为一连续的不确定变量，并与各部件的寿命相互独立，当开关失效时，系统立即失效.显然，该冷贮备系统的寿命为

相应地，可以计算其可靠度为

平均寿命为

例4 若该冷贮备系统由2个部件X1，X2和开关XK构成，且X1～L（2，6），X2～L（3，5），XK～Z（2，4，5），由式（3）可知X1+X2～L（5，11），首先计算

因此，该冷贮备系统的可靠度为

平均寿命为

4 结 语

对于概率论无法处理的系统可靠性问题，不确定理论为其提供了有效的解决办法.不确定理论是基于规范性、单调性、自对偶性、可列次可加性的数学分支.本文将不确定理论应用于不可修冷贮备系统的建模和可靠性分析中，给出了评定系统可靠性的主要数量指标的数学表达式.由于转换开关的好坏是影响系统可靠度的一个重要因素，根据文中算例可知，在部件寿命分布相同的情况下，转换开关完全可靠的冷贮备系统可靠度和平均寿命高.在以后的研究中，将对不确定环境下可修系统进行建模和可靠性分析，并给出可靠性数量指标的表达式.

［1］ Barlow R E，Proschan F. Statistical Theory of Reliability and Life Testing：Probability Models［M］. New York：Holt，Rinehart and Winston，1975.

［2］ Gnedenko B V，Belyayev Y K，Solovyev A D. Mathe-matical Methods of Reliability Theory［M］. New York：Academic Press，1969.

［3］ 曹晋华，程侃. 可靠性数学引论［M］. 北京：高等教育出版社，2012.

［4］ 李玉亚. 可靠性数学［M］. 武汉：华中理工大学出版社，1999.

［5］ Liu B D. Uncertainty Theory［M］. 2nd ed.Berlin：Springer-Verlag，2007.

［6］ Huang X X. Mean-risk model for uncertain portfolio selection［J］. Fuzzy Optimization and Decision Making，2011，10（1）：71-89.

［7］ Gao Y. Uncertain inference control for balancing an inverted pendulum［J］. Fuzzy Optimization and Decision Making，2012，11（4）：481-492.

［8］ Zhang B，Peng J. Uncertain programming model for uncertain optimal assignment problem［J］. Applied Mathematical Modelling，2013，37（9）：6458-6468.

［9］ Han S W，Peng Z X，Wang S Q. The maximum flow problem of uncertain network［J］. Information Sciences， 2014，265（1）：167-175.

［10］ Yang L X，Liu P，Li S K，et al. Reduction methods of type-2 uncertain variables and their applications to solid transportation problem［J］. Information Sciences，2015，291（10）：204-237.

［11］ Liu Y，Li X Z，Xiong C C. Reliability analysis of unrepairable systems with uncertain lifetimes［J］. International Journal of Security and Its Applications，2015，9（12）：289-298.

［12］ Liu Y，Zhu H M. Reliability analysis of fuzzy unrepairable systems［J］. Information：An International Interdisciplinary Journal，2012，15（10）：3935-3944.

［13］ Liu Y，Li X Z，Yang G L. Reliability analysis of random fuzzy unrepairable cold standby systems with imperfect conversion switches［J］. Information：An International Interdisciplinary Journal，2011，14（2）：283-296.

［14］ Liu B D. Uncertainty Theory：A Branch of Mathematics for Modeling Human Uncertainty［M］. Berlin：Springer-Verlag，2010.

责任编辑：常涛

Reliability Analysis of Unrepairable Cold Standby Systems Based on Lifetime Uncertainty

LIU Ying，MA Yao，WANG Lin
（College of Computer Science and Information Engineering，Tianjin University of Science & Technology，Tianjin 300222，China）

When there are not enough samples for the lifetime of unrepairable cold standby systems，the lifetimes of components in the cold standby systems were used as independent and nonnegative uncertainty variables in this research.The basic mathematical models of three unrepairable cold standby systems were developed.They are the unrepairable cold standby system with absolutely reliable conversion switches，the unrepairable cold standby system with 0-1 mode conversion switches，and the unrepairable cold standby system with continuous mode conversion switches.Reliability analysis of the three unrepairable cold standby systems was conducted，respectively，and the expressions of reliability and mean time to failure（MTTF）of the three cold standby systems were realized.Finally，some numerical examples were given for illustration. Key words：uncertainty theory；unrepairable systems；reliability；mean time to failure；cold standby system

N945

A

1672-6510（2016）05-0074-05

10.13364/j.issn.1672-6510.20150232

2015-12-05；

2016-04-24

国家自然科学基金资助项目（11301382）；天津科技大学青年教师创新基金资助项目（2014CXLG28）

刘 颖（1982—），女（回），天津人，副教授，liu@tust.edu.cn.