炔雌醇多晶型非等温转晶动力学研究

李先朝，朱 亮，，王立宇，沙作良

（1. 天津科技大学化工与材料学院，天津 300457；2. 迈安德集团有限公司，扬州 225127）

炔雌醇多晶型非等温转晶动力学研究

李先朝1，朱 亮1，2，王立宇1，沙作良1

（1. 天津科技大学化工与材料学院，天津 300457；2. 迈安德集团有限公司，扬州 225127）

通过冷却结晶制备炔雌醇晶型Ⅰ，并采用X射线粉末衍射（XRPD）、拉曼光谱分析（Raman）以及差示扫描量热（DSC）对炔雌醇晶型进行分析表征；采用非等温差示扫描量热法对炔雌醇晶型Ⅰ升温晶型转变过程进行了系统研究.实验结果表明：炔雌醇晶型Ⅰ在热介导条件下可转化为晶型Ⅱ.结合炔雌醇晶型Ⅰ晶型转变过程实验数据，确定了炔雌醇晶型转变过程机理：随机成核和随后生长，n=1/4；机理函数的微分表达式和积分表达式分别为f（α）=4（1-α）［-ln（1-α）］3/4和G（α）=［-ln（1-α）］1/4.

炔雌醇；多晶型；晶型转变；转晶动力学

炔雌醇为3-羟基-19-去甲-17α-孕甾-1，3，5（10）-三烯-20-炔-17-醇［1-3］.炔雌醇为白色或类白色的结晶性粉末，无臭，是一种强效雌激素.炔雌醇是口服避孕药中最重要的雌激素，作用同乙烯雌酚，但效力强20倍.其与孕激素配伍，对抑制排卵有协同作用，增强避孕效果，并可减小突破性出血等副作用［2，4］.炔雌醇在激素替代疗法中曾被广泛应用，对因避孕所致月经紊乱等不良反应也有明显治疗效果.

Guguta等［5］通过进行广泛的结晶实验，报道了炔雌醇多种溶剂化合物（包含的溶剂分别为水、甲醇、乙腈以及二氧六环等）.Karpinska等［6］通过在真空中低温梯度升华，首次得到了炔雌醇的无溶剂化结晶，并得到3种溶剂化合物，包含的溶剂分别为丙酮、二甲基亚砜以及2-戊醇.现有文献对炔雌醇报道的仅仅是晶型筛选工作，针对炔雌醇多晶型之间存在晶型转变的文献未见报道.本文以甲醇和水为混合溶剂，通过冷却结晶方式制备得到了炔雌醇晶型Ⅰ.同时利用差示扫描量热（DSC）在升温过程对炔雌醇晶型Ⅰ进行了非等温转晶动力学研究，并利用Kissinger-Akahira-Sunose（KAS）方法求得其非等温转晶活化能，以最小偏差法得到最可能的机理函数.

1 材料与方法

1.1 实验原料

炔雌醇（纯度≥99%），华润紫竹药业有限公司，经重结晶精制；无水甲醇，分析纯，博欧特（天津）化工贸易有限公司；蒸馏水，天津腾达化学试剂公司.

1.2 炔雌醇样品的处理

将炔雌醇粗品溶解于V（甲醇）∶V（水）=1∶1的混合溶剂中，配制成饱和溶液，通过冷却结晶方式制备得到炔雌醇晶型Ⅰ.炔雌醇晶型Ⅰ在150，℃高温下干燥可以转化成炔雌醇晶型Ⅱ.

1.3 表征方法及条件

1.3.1 X射线粉末衍射（XRPD）分析

采用Lab MALS XD-3型衍射仪进行分析，配有石墨单色器；Cu靶Kα射线（λ=0.154，056，nm）；工作电压40，kV，工作电流40，mA；扫描范围5°～40°，步长0.02°，扫描速率1 °/min.

1.3.2 拉曼光谱（Raman）分析

采用Lab RAM HR800型激光显微共聚焦拉曼光谱仪（法国Horiba JOBIN YVON公司）进行分析，激发光源：20，mW，He-Ne，激发波长532，nm，扫描范围100～4，000，cm-1，曝光时间5，s，扫描次数2次. 1.3.3 差示扫描量热分析

采用DSC 200，F3型差示扫描量热仪（德国NETZSCH 公司）进行相关测定.铝坩埚，氮气气氛，流量50，mL/min；升温范围为25～200，℃，升温速率分别为10、15、20、30，K/min.

1.3.4 热重（TGA）分析

采用TGA/DSC 1/SF型热重分析仪（瑞士Mettler Toledo公司）进行分析，Al2O3坩埚，升温范围为25～550，℃，升温速率为10，K/min，气氛为氮气.

2 基本原理

2.1 等转化率法

任何非等温动力学分析（DSC、DTA、TG等）都以速率方程为基础［7-8］

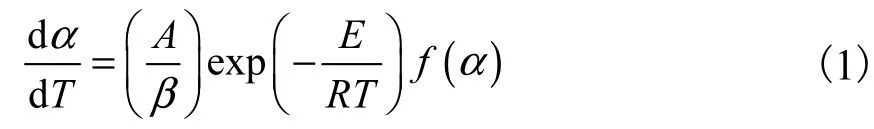
式中：α 为转化率；f（α）为动力学机理函数；β为升温速率，K/min；E为活化能，kJ/mol；A为指前因子，s-1；T为该转化率下的反应温度，K；R为气体常数，

温度积分公式P（x）在数学上得到不精确解，常由近似公式代替.采用Coats-Redfern近似式［9-10］得到Kissinger-Akahira-Sunose（KAS）方程［11］R=8.314，J/（mol·K）.

设x=E/RT，对式（1）进行移项并两端同时进行积分得

2.2 判定最可能的机理函数

主曲线法［12］是判定最可能的机理函数一种常用的方法，它是以实验曲线和理论曲线的最大重合作为判定的依据；最小偏差法则是以实验值和理论值大小差别作为判定的依据［8，12-14］.本文以最小偏差法来求算炔雌醇晶型相转变最可能的反应机理函数，其过程如下：

以α=0.5作为参考点［15］，由式（2）可以得到

同时，本文采用温度积分近似表达式［16-17］来计算P（x）：

将KAS方程计算得到每个转化率下的活化能以及转化率所对应的温度T值代入式（4）右端，计算出P（x）/P（x0.5）的值，作为实验值；将表1中的反应机理对应的G（α）代入式（4）的左端计算出G（α）/G（0.5）的值，作为理论值.计算实验值和理论值之间的标准偏差，根据计算出的标准偏差大小来确定合适的反应机理函数.当某一个反应机理能够精确地描述实验结果时，其标准偏差数值最小.

标准偏差（SD）采用式（6）计算［12］.

式中：m和n分别为数据点和升温速率的数目；k为表中反应机理的序号.

表1 常用的非均相反应的动力学模型Tab. 1 Kinetic model usually employed for the solid-state reaction

3 结果与讨论

3.1 炔雌醇多晶型的表征

炔雌醇晶型XRPD谱图如图1所示.

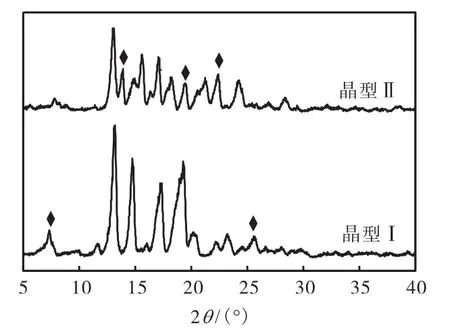
图1 炔雌醇晶型XRPD谱图Fig. 1 XRPD patterns of EE

由图1可知：炔雌醇晶型Ⅰ在2θ为7.299°、25.659°等峰位存在典型的特征峰；炔雌醇晶型Ⅱ在2θ 为13.840°、18.260°、22.317°等峰位存在典型的特征峰，这些特征峰可以作为区别炔雌醇晶型的依据.图2拉曼图谱结果显示，炔雌醇晶型Ⅰ与晶型Ⅱ的不同在于炔雌醇晶型Ⅱ在2，100，cm-1处出现双特征峰，而晶型Ⅰ是单峰，晶型Ⅰ在3，600，cm-1附近处无特征峰，但晶型Ⅱ在此处有2个明显的特征峰.图3是升温速率为10，K/min时炔雌醇晶型Ⅰ和Ⅱ在25～200，℃的DSC曲线，从图3可以看出炔雌醇晶型Ⅰ在147.6，℃和183，℃附近产生2个吸热峰，但在147.6，℃附近同时存在吸热峰和放热峰.而炔雌醇晶型Ⅱ仅在183，℃有一个吸热峰.

图2 炔雌醇晶型拉曼谱图Fig. 2 Raman spectral of EE

图3 升温速率为10，K/min时炔雌醇晶型的DSC曲线Fig. 3 DSC curves of EE at the heating rate of 10，K/min

图4是升温速率为10，K/min时炔雌醇晶型Ⅰ和Ⅱ在25～550，℃的TGA曲线，可以看出炔雌醇晶型Ⅰ无脱溶剂平台，仅在200，℃开始发生热分解，可以判断晶型Ⅰ非溶剂化合物.晶型Ⅰ热分解有2个阶段：第一阶段从200，℃开始到320，℃结束，第二阶段从320，℃左右开始到500，℃左右热分解完成.同时可以看出炔雌醇晶型Ⅱ同样存在2个热分解阶段：第一阶段从230，℃到365，℃结束，第二阶段从365，℃开始到500，℃左右热分解完成.

图4 升温速率为10，K/min时炔雌醇晶型的TGA曲线Fig. 4 TGA curves of EE at the heating rate of 10，K/min

3.2 炔雌醇晶型转变动力学

在通过差示扫描量热法进行非等温转晶分析过程中，首先需要确定转化率α，转化率可以表述为指定温度下的结晶放热曲线积分面积除以整个曲线的积分面积［18］.上述过程可以采用式（7）表示.

式中：α 为转化率，T0、T1及T分别为结晶曲线的起始温度、某时刻温度及终止温度.

不同升温速率下25～200，℃内炔雌醇晶型Ⅰ的DSC曲线如图5所示.

图5 不同升温速率下炔雌醇晶型Ⅰ的DSC曲线Fig. 5 DSC curves of crystal formⅠof EE at different heating rates

由图5可知：随着升温速率增加，放热峰的峰强逐渐增大且转晶初始温度向更高温度偏移.同时根据DSC曲线所对应的数据，依据等转化率法来确定动力学参数，使用KAS方程对炔雌醇晶型Ⅰ相转变过程的活化能E进行计算.通过转化率α 分别依据式（2）和式（3）即可求取动力学参数.在不同转化率α下，以1，000/T 为横坐标，ln（β/T2）为纵坐标对数据点进行拟合，结果如图6所示.

图6 不同转化率下KAS方程作图Fig. 6 KAS plot of EE with different values of conversion

由图6中拟合得到线性斜率可以分别计算出KAS方程所得到的活化能E以及线性相关系数R2.由图7结果可知：KAS方程得到的活化能随着转化率α 的提高逐渐减小，变化范围为243～359，kJ/mol，这意味着炔雌醇相转变过程反应机理不是恒定不变的，且活化能与转化率α 有关.结果还表明，KAS方法能够很好地描述炔雌醇晶型Ⅰ转晶过程.

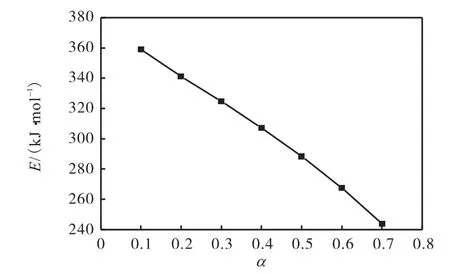
图7 活化能随转化率的变化Fig. 7Activation energy along with the change of the conversion

采用2.2中所述的方法，将实验数据代入式（4）右端，计算得到P（x）/P（x0.5）的值，构成实验值，将表1中列出的机理对应的G（α）代入式（4）左端计算出G（α）/G（0.5）的值，构成理论值.根据最小偏差法对实验值和理论值进行处理，表1中列出了各种机理函数所对应的标准偏差.由表1中数据可知函数8所对应的标准偏差最小，应为炔雌醇晶型转变过程的最可能的机理，函数方程是Avarmi-Erofeev，该机理为随机成核和随后生长机理，n=1/4.对应的机理函数为G（α）=［-ln（1-α）］1/4，相对应的微分形式为f（α）= 4（1-α）［-ln（1-α）］3/4.

4 结 论

采用非等温差示扫描量热法得到炔雌醇晶型Ⅰ的晶型转变过程符合Avarmi-Erofeev公式；采用最小偏差法得到炔雌醇晶型Ⅰ晶型转变最可能机理函数，机理为随机成核和随后生长，n=1/4，机理函数的微分表达式和积分表达式分别为f（α）=4（1-α）［-ln（1-α）］3/4和G（α）=［-ln（1-α）］1/4.

［1］ 宁丽峰，徐娟，郭颖志，等. 女性口服避孕药物多晶型的研究进展［J］. 中国计划生育学杂志，2014，22（5）：349-351.

［2］ 王彦坤，宁美英，刘有平. 炔雌醇固体分散体的制备及性质考察［J］. 中国新药杂志，2014，23（4）：470-475.

［3］ Pheasant R. Polymorphism of 17-ethinylestradiol［J］. Journal of the American Chemical Society，1950，72（9）：4303-4304.

［4］ 闫胜英，李琳，侯连云. 乙炔雌二醇治疗皮下埋植避孕法所致月经紊乱［J］. 山西职工医学院学报，2008，18（3）：39-40.

［5］ Guguta C，Eeuwijk I，Smits J M M，et al. Structural diversity of ethinyl estradiol solvates［J］. Crystal Growth & Design，2008，8（3）：823-831.

［6］ Karpinska J，Erxleben A，McArdle P. Applications of low temperature gradient sublimation in vacuo：Rapid production of high quality crystals. The first solvent-free crystals of ethinyl estradiol［J］. Crystal Growth & Design，2013，13（3）：1122-1130.

［7］ Budrugeac P，Segal E. Some methodological problems concerning nonisothermal kinetic analysis of heterogeneous solid-gas reactions［J］. International Journal of Chemical Kinetics，2001，33（10）：564-573.

［8］ Lu X C，Li H Y，Xiao P L，et al. The kinetic analysis of the non-isothermal crystallization process of （Zr46，Cu42Al7Y5）95Be5metallic glass［J］. Thermochimica Acta，2013，570：27-32.

［9］ Coats A W，Redfern J P. Kinetic parameters from thermogravimetric data［J］. Nature，1964，201：68-69.

［10］ Coats A W，Redfern J P. Kinetic parameters from thermogravimetric data. Ⅱ［J］. Journal of Polymer Science Part B：Polymer Letter，1965，3：917-920.

［11］ Slopiecka K，Bartocci P，Fantozzi F. Thermogravimetric analysis and kinetic study of poplar wood pyrolysis［J］. Applied Energy，2012，97：491-497.

［12］ 周佳，何明中，张爱华，等. 高岭土相转变的非等温动力学［J］. 无机化学学报，2010，26（7）：1279-1283.

［13］ Yang H C，Cho Y J，Eun H C，et al. Kinetic study of a thermal dechlorination and oxidation of neodymium oxychloride［J］. Thermochimica Acta，2007，460（1/2）：53-59.

［14］ 曾远，何明中，周佳，等. 迪开石热分解及重结晶的非等温动力学［J］. 高等化学学报，2011，32（12）：2865-2871.

［15］ 唐万军，陈栋华，伍明. 草酸亚锡热分解反应动力学［J］. 中南民族大学学报：自然科学版，2007，26（1）：16-19.

［16］ 唐万军，陈栋华. 二水草酸亚铁分解反应动力学［J］.物理化学学报，2007，23（4）：605-608.

［17］ Senum G I，Yang R T. Rational approximations of the integral of the Arrhenius function［J］. Journal of Thermal Analysis，1977，11（3）：445-447.

［18］ Grooff D，De Villiers M M，Liebenberg W. Thermal methods for evaluating polymorphic transitions in nifedipine［J］. Thermochimica Acta，2007，454（1）：33-42.

责任编辑：周建军

Non-isothermal Kinetics of Polymorphic Transition of Ethinyl Estradiol

LI Xianchao1，ZHU Liang1，2，WANG Liyu1，SHA Zuoliang1
（1.College of Chemical Engineering and Materials Science，Tianjin University of Science & Technology，Tianjin 300457，China；2.Myande Group Co.，Ltd.，Yangzhou 225127，China）

Crystal form Ⅰof ethinyl estradiol was prepared through cooling crystallization and characterized by X-ray powder diffraction（XRPD），raman spectrometry and differential scanning calorimetry（DSC）.Non-isothermal kinetics of ethinyl estradiol in the transformation process of crystal formⅠwas systematically investigated，using DSC technique.The results indicate that formⅠof ethinyl estradiol can be transformed into crystal formⅡunder heat mediated conditions.Based on the experimental data and different kinetic functions of corresponding polymorphic transition mechanism，the polymorphic mechanism of ethinyl estradiol was analyzed and estimated.It is found that nuclei production and nuclei growth model，n=1/4，can best describe the ethinyl estradiol polymorphic transformation process.The corresponding mechanic functions of differential expression and the integral expression are f（α）=4（1-α）［-ln（1-α）］3/4and G（α）=［-ln（1-α）］1/4，respectively. Key words：ethinyl estradiol；polymorphism；polymorphic transition；transformation kinetics

O792； R9

A

1672-6510（2016）05-0047-05

10.13364/j.issn.1672-6510.20150087

2015-07-06；

2015-12-24

天津市应用基础与前沿技术研究计划资助项目（14JCZDJC40900）

李先朝（1988—），男，安徽人，硕士研究生；通信作者：朱 亮，副教授，zhuliang@tust.edu.cn.