水平井体积改造应力干扰计算模型及其应用

胥云，陈铭，吴奇，，李德旗，杨能宇，翁定为，管保山

（1. 中国石油勘探开发研究院廊坊分院；2. 中国石油天然气股份有限公司油气藏改造重点实验室；3. 中国石油勘探开发研究院；4. 中国石油勘探与生产分公司；5. 中国石油浙江油田公司）

水平井体积改造应力干扰计算模型及其应用

胥云1，2，陈铭1，3，吴奇2，4，李德旗5，杨能宇4，翁定为1，2，管保山1，2

（1. 中国石油勘探开发研究院廊坊分院；2. 中国石油天然气股份有限公司油气藏改造重点实验室；3. 中国石油勘探开发研究院；4. 中国石油勘探与生产分公司；5. 中国石油浙江油田公司）

基于位移不连续边界元法，引入应力校正因子，建立裂缝介质应力场计算模型。模型计算精度与三维位移不连续模型接近，并显著减小了计算复杂度。在此基础上，基于断裂准则和扩展速度模型，建立了多裂缝扩展形态算法，对多裂缝应力干扰及应力干扰下裂缝扩展形态进行了计算研究。结果表明：应力干扰作用范围由缝高或缝长的最小尺寸决定，对缝长大于缝高的裂缝，应力干扰作用范围为1.2～1.5倍缝高，对缝长小于缝高的裂缝其范围为1.2～1.5倍缝长；缝间距相对缝高越大或净压力相对原场主应力差越小，裂缝偏转位置距离井筒越远，裂缝偏转角度越小。3簇等间距布缝时，中间裂缝沿直线路径扩展，而非等间距布缝时，中间裂缝会向间距远的裂缝一侧偏转，且存在单一主扩展裂缝。图9参26

水平井；体积改造；应力干扰；位移不连续法；裂缝偏转；多簇扩展；不等间距布缝

0 引言

体积改造应力干扰是水力裂缝张开或滑移对原场应力的扰动，又称水力裂缝诱导应力或应力阴影作用［1-2］。认清体积改造应力干扰作用规律及应力干扰作用下多裂缝扩展形态，对于体积改造优化设计［3-4］、产能预测具有重要意义。

早期Sneddon［5］、Green［6］、Pollard等［7］给出了二维平面应变裂缝应力场解析解，但解析解只适用于二维平直裂缝，不能用于复杂裂缝应力场计算。复杂裂缝应力场的计算需采用数值计算方法。常用数值方法包括有限元、有限差分、有限体积、离散元和边界元方法。其中前4种方法均需对整个求解域进行离散求解，计算量较大，而边界元方法将全场问题转化为边界问题，只需将边界离散而显著减小了解题规模，尤为适合无限大介质中裂缝和断裂问题［8-9］。1976年Crouch［10］建立了二维位移不连续边界元法，1993年Shou［11］引入裂尖渐近解，建立了三维位移不连续边界元法，但计算量显著增大。2004年Olson［12］提出了拟三维不连续边界元法，但忽略了对裂缝宽度的处理。Weng等［13］的非常规压裂模型（UFM）及Wu等［14］的裂缝扩展模型均采用Olson模型求解岩体变形，因存在计算误差而影响施工决策。

针对应力场计算模型的不足，本文基于二维位移不连续边界元法，引入应力校正因子，建立裂缝介质的应力场计算模型，并与三维位移不连续模型对比，验证模型的可靠性。基于断裂力学方法，显式求解多裂缝扩展速度，给出了多缝扩展形态算法，并对应力干扰以及应力干扰作用下裂缝扩展形态进行了影响因素分析和实例研究。

1 计算模型

1.1 模型建立

位移不连续边界元法是基于位移不连续单元基本解的数值方法，其基本原理类似于渗流力学格林函数法。对于缝长为L，高度为H的三维非平面裂缝（见图1），沿缝长将裂缝等分为N个单元，每个单元的半长为a，某个单元的中心点坐标为（xi，yi），i=1，2，…，N。对于半长为a的单元，其位移不连续定义为［10］：

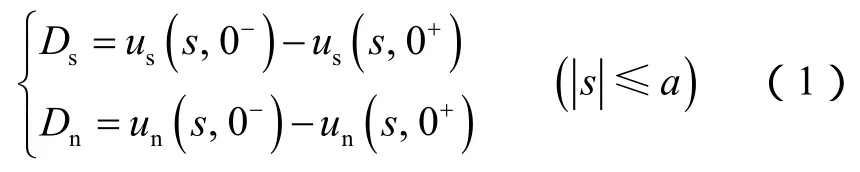
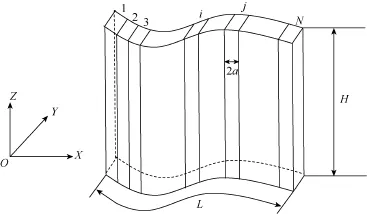
图1 坐标及裂缝示意图

根据位移不连续基本解［10］，j单元位移不连续产生的应力为：

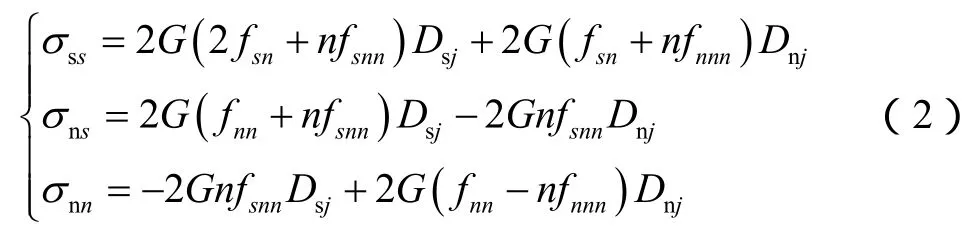
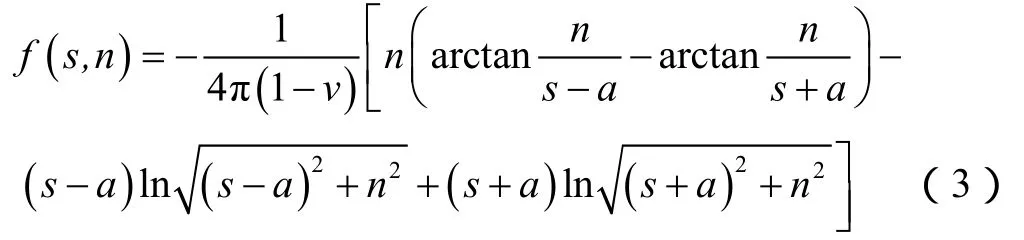
i单元中心点在j单元局部坐标系内的坐标为：

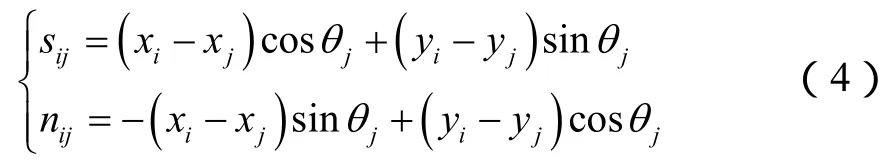
根据应力坐标转换［15］，将（2）式应力分量转换到i单元局部坐标系，可得Dsj、Dnj在i单元产生的法向和切向应力为：

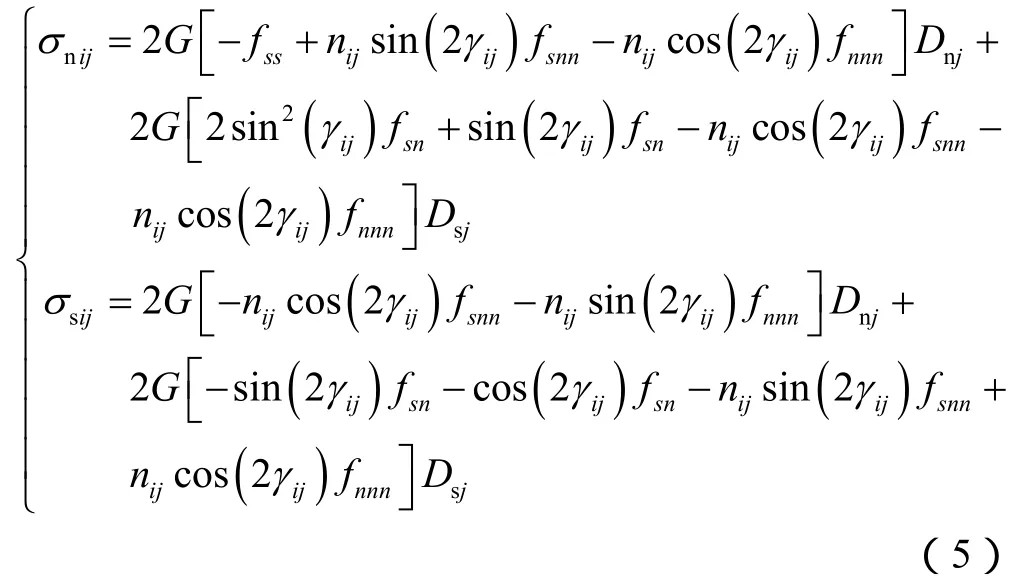
其中 γij=θi- θj

将（5）式简记为：

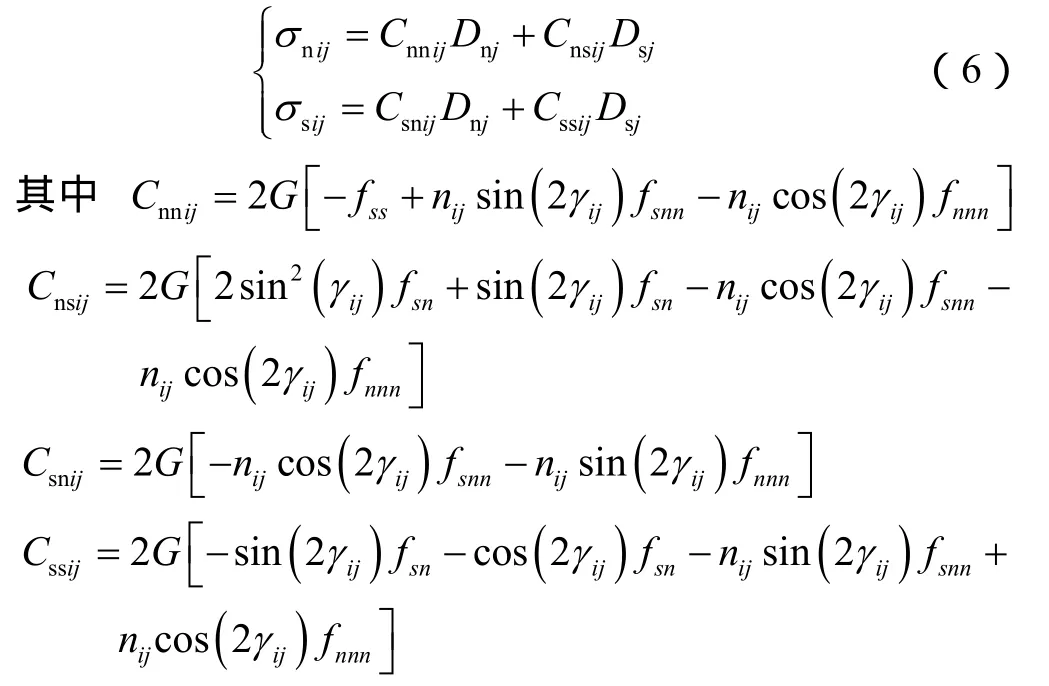
根据叠加原理，N个位移不连续量在i单元产生的应力为：

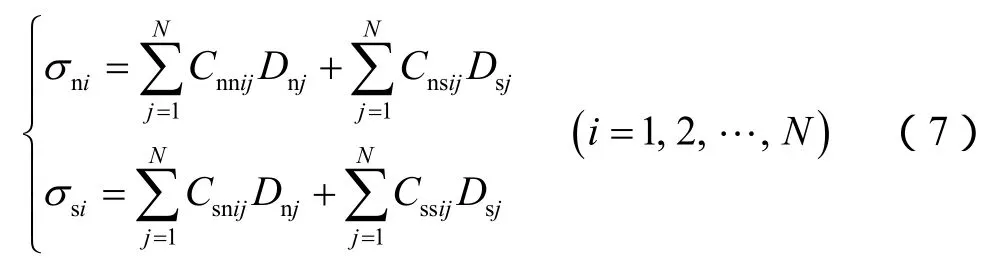
以上是长度方向离散得到位移不连续计算模型，其中应力影响系数未考虑缝高的影响。为不增加计算复杂度，通过修正（7）式的应力影响系数来考虑缝高的影响。根据弹性力学的推导，对于高度为H的平面裂缝，垂直于裂缝面方向（y轴）的应力［16］为：

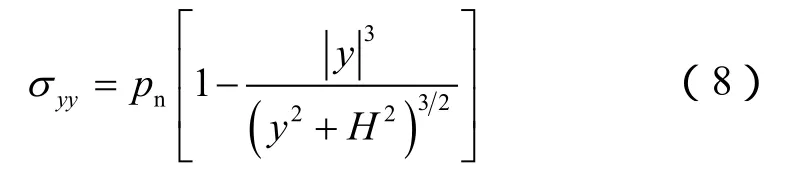
根据（8）式描述的缝高影响下的应力分布形式，引入应力校正因子：

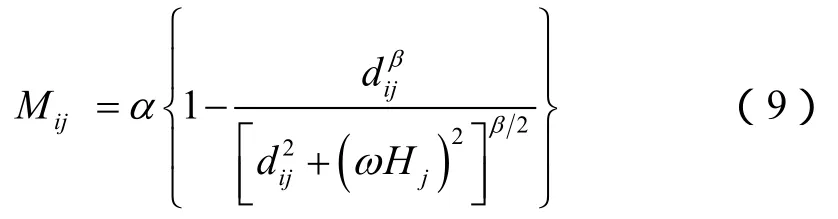
将应力校正因子与（6）式或（7）式中应力影响系数相乘［17］，即得到修正的应力影响系数。修正的应力影响系数在缝长应力影响系数基础上，考虑了高度方向应力影响特征。根据应力影响系数的修正方法，得到三维裂缝的应力场计算模型：

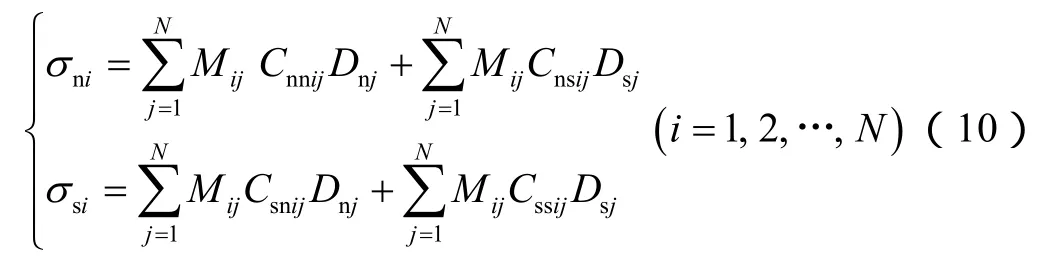
通过试算分析，确定采用修正系数α=2，β=2，ω=1.2可得到较好的计算结果。

1.2 模型验证与对比

1.2.1 准确性验证与对比

为了验证计算模型的可靠性，采用三维位移不连续法（3D DDM）［11］、Olson的计算模型与本文模型计算对比。算例参数：裂缝高度50 m，半长150 m，净压力5 MPa，弹性模量为35 320 MPa，泊松比为0.2，图2为裂缝宽度分布和垂直裂缝面（沿y轴）的应力σyy分布。

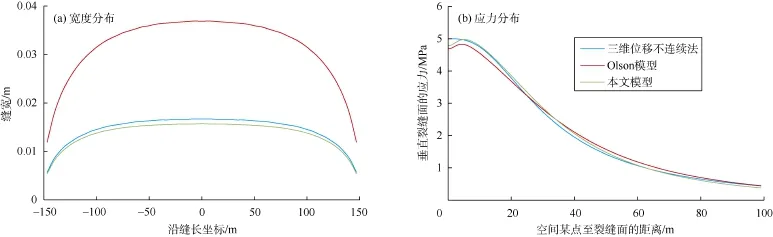
图2 模型计算结果对比

由图2可见，Olson模型应力计算接近3D DDM，但裂缝宽度的计算结果显著偏离3D DDM结果；而本文模型裂缝宽度和应力计算结果均接近3D DDM。由于裂缝宽度的计算是水力压裂模型的重要部分，裂缝宽度影响水力裂缝尖端位置、缝长和导流能力的计算，因此采用Olson模型必然存在较大误差。新模型不存在Olson计算模型的不足，可用于裂缝应力场和缝宽的计算。

1.2.2 计算量对比

3D DDM在求解裂缝问题时需将裂缝沿长度和高度方向离散，每个单元具有3个未知量（1个法向和2个切向位移不连续量）。本文模型和Olson模型均只对长度方向进行离散，每个单元有两个未知量。假设沿缝长方向离散为NL个单元，沿缝高方向离散为NH个单元，则3D DDM总共有3NLNH个未知量，对应矩阵方程的阶为3NLNH。由于该边界元矩阵方程为稠密矩阵，迭代法（高斯-赛德尔迭代等）并不适用，采用直接法（高斯-约当消去法等）求解矩阵方程的计算量约为（3NLNH）3/3+0.5（3NLNH）2；本文模型和Olson模型仅沿长度方向离散，共有2NL个未知量，直接法求解矩阵方程的计算量约为（2NL）3/3+0.5（2NL）2。图3为3种模型计算量对比，3D DDM缝高离散单元数取10。结果显示，3D DDM计算量显著高于本文和Olson模型，若缝高离散数量NH增大，计算量将更大，不利于工程应用。

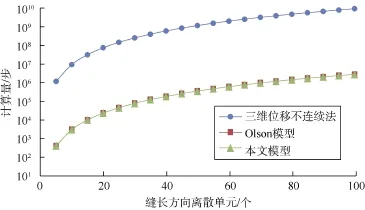
图3 模型计算量对比

综合计算精度和计算量分析，本文模型在保证计算量相对3D DDM较小的情况下，计算应力和缝宽均较为准确，可用于工程计算。

1.3 多裂缝扩展形态计算

裂缝扩展形态的计算采用Roussel［18］、Olson［19］等的假设，即不考虑流动摩阻和滤失，考察恒定高度裂缝在缝间应力干扰作用下扩展形态。矿场尺度下水力压裂裂缝扩展通常处于黏度控制阶段［20］，裂缝应力强度因子小于其断裂韧性时也会发生扩展。根据Pollard［21］、Olson［22］等研究，采用亚临界扩展模型计算扩展速度：

Ⅰ—Ⅱ复合型裂缝尖端应力强度因子［23］为：

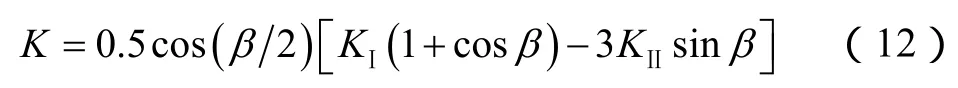
其中Ⅰ型、Ⅱ型应力强度因子通过缝尖位移不连续量确定［24］。

裂缝扩展角度φ采用最大周向应力准则［23］确定：

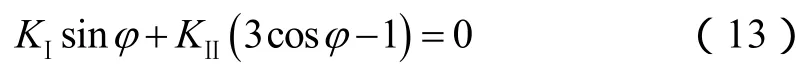
多裂缝同步扩展情况下，多条裂缝尖端根据扩展速度增加单元长度。需要注意的是，非等单元条件下，裂缝尖端应力强度因子存在较大误差。为了避免裂缝非等单元扩展，对多裂缝同步扩展处理方法为：计算各缝尖应力强度因子，确定各自扩展速度，将各缝尖扩展速度进行排序，最大扩展速度的缝尖增加一个单元，其他缝尖则根据其扩展速度累计单元增量，当累计单元增量达到一个扩展单元时，进入位移不连续裂缝扩展模型的计算部分，否则累计缝长直到一个扩展单元。由于裂缝体积等于注入液量，因此以裂缝体积达到注入液量为计算终止判定条件。

2 模型应用

2.1 应力干扰作用范围理论分析

由图4可知，应力干扰作用范围与裂缝形态有关。当L/H=1时，应力干扰作用范围为50 m；当L/H为3、5、10时，应力干扰作用范围为60～75 m，满足1.2～1.5倍裂缝高度，表明缝长大于缝高时，增大缝长不会扩大应力干扰作用范围，应力干扰作用范围由裂缝面最小尺寸——缝高确定；而缝长小于缝高时，如L/H为0.2、0.5时，应力干扰作用范围为15～32 m。应力干扰作用距离不再为1.2～1.5倍缝高，而是1.2～1.5倍缝长，表明裂缝长度小于高度时，应力干扰作用范围与缝高无关，由裂缝面最小尺寸——缝长确定。

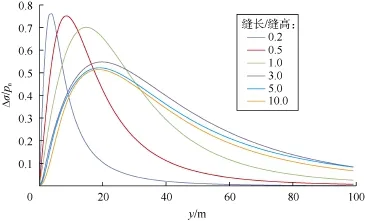
图4 不同尺寸裂缝的Δσ/pn与y关系

综上，应力干扰作用范围由裂缝面最小尺寸确定。由于水力裂缝通常缝长大于缝高，因此，水力裂缝应力干扰作用范围通常受控于缝高；在缝高过量增长的情况下，应力干扰作用范围将受控于缝长。

应力干扰作用范围实质上为三维应力向二维应力转化的结果。当缝长大于缝高时，垂直于缝长的截面近似为平面应变，缝高是控制岩体变形的特征量，应力场则受缝高影响；缝长小于缝高时，垂直于缝高的截面近似为平面应变，缝长是控制岩体变形的特征量，应力场则受缝长影响。

2.2 多簇裂缝扩展形态因素分析

结合国内体积改造的主要做法［24，26］，以2簇和3簇压裂为例分析多簇裂缝扩展形态。计算参数：注入液量300 m3，弹性模量35 320 MPa，泊松比0.2，主应力差5 MPa，净压力5 MPa，裂缝高度30 m，裂缝间距30 m，亚临界指数1。由于水力压裂缝通常缝长大于缝高，根据上述研究，该情况下应力干扰作用范围由裂缝高度决定，因此以缝间距和缝高作为一组因素分析。净压力是应力干扰作用的来源，其改变原地应力场的程度取决于原场主应力大小，因此将净压力与主应力差作为一组因素分析。

根据选择参数进行模拟计算。结果表明（见图5）：2簇裂缝扩展时，裂缝相互背离偏转，偏转角度约为3.15°；3簇裂缝扩展时，两侧裂缝在30 m附近发生约1.95°背离偏转，中间裂缝沿直线扩展，但扩展长度小于两侧裂缝，约为两侧裂缝长度的53%。

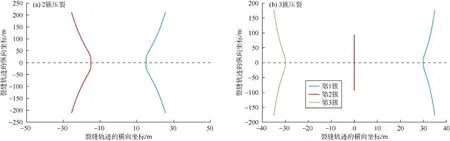
图5 多簇压裂裂缝扩展形态

为考察裂缝偏转的影响，采用偏转位置和偏转角度来表征。偏转位置为裂缝发生偏转时与井筒的距离，平均偏转角度为偏转方向与原扩展方向的平均夹角。

2.2.1 缝间距与缝高的影响

3簇裂缝扩展时，两侧裂缝的偏转规律与2簇裂缝扩展规律相同，因此参数敏感性分析以两簇裂缝扩展为例。

由图6可见，缝间距20 m、缝高50 m时，裂缝偏转位置距离井筒最近，为18.5 m，同时偏转角最大。缝高20 m、缝间距40 m或缝高30 m、缝间距50 m时，裂缝不发生偏转，表明该条件下应力干扰作用可以忽略不计。

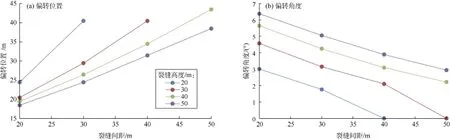
图6 不同裂缝高度下裂缝偏转位置和偏转角度与裂缝间距的关系

研究结果表明，裂缝高度与缝间距存在最佳匹配关系。对于一定高度的裂缝，裂缝间距越大，发生偏转的位置距井筒越远（即偏转时间越晚），偏转角度越小。而间距一定的情况下，增大裂缝高度会减小裂缝偏转位置，增大裂缝偏转角度。

2.2.2 净压力与主应力差的影响

改变净压力与主应力差，研究净压力与主应力差对裂缝偏转形态的影响。由图7可见，裂缝最小偏转位置为22.5 m，最大偏转角为7.19°。净压力为20 MPa，主应力差为5 MPa时，偏转位置距离井筒最近、偏转角度最大。净压力为5 MPa时，不同主应力差下裂缝偏转位置为29.5～39.5 m；净压力为10 MPa时，不同主应力差下偏转位置为25.5～39.5m，偏转角度为1.8°～5.1°；净压力为15 MPa时，偏转位置范围为23.5～32.5 m，偏转角度为2.5°～6.3°；净压力为20 MPa时，偏转位置范围为22.5～28.5 m，偏转角度为3.2°～7.2°。

结果表明：主应力差和净压力是影响裂缝偏转的关键因素。净压力相对主应力差越小，发生偏转的位置距离井筒越远，偏转角度越小。

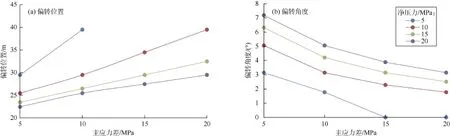
图7 不同净压力下偏转位置和偏转角度与主应力差的关系

2.2.3 非等间距布缝的影响

实际作业中，由于地层复杂性或射孔不完善性，多簇裂缝不可避免会出现非等间距分布的情况。取裂缝高度50 m，3簇裂缝簇间距依次为d1/d2=2/1、d1/d2=1/2，研究裂缝扩展形态。由图8可知，由于缝间距的存在，裂缝扩展不均匀程度增大，并存在一条主扩展裂缝。主扩展裂缝为距离其他裂缝均较远的裂缝。中间裂缝不再恒为直线路径扩展，而是先沿直线延伸20 m，然后向距中间裂缝较远的裂缝偏转，偏转角度接近90°。

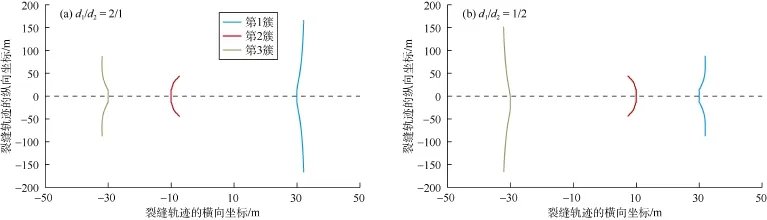
图8 非等间距布缝裂缝扩展形态

等间距分布裂缝时，中间裂缝受到两侧裂缝对称应力作用，因此中间裂缝为单一张型裂缝，裂缝沿直线路径扩展；而非等间距分布裂缝时，中间裂缝受到两侧裂缝不均衡的应力作用，不再为单一张型裂缝，因此中间裂缝偏离直线路径扩展。同时，中间裂缝受近距离裂缝的应力干扰作用更加强烈，因此会向间距较远的裂缝偏转。

对于非均质储集层，可采用多簇非等间距布缝，将主扩展裂缝置于“甜点”区，提高甜点改造程度；对于较为均质的储集层，可等间距布缝，避免出现单一裂缝过量延伸而影响改造效果。

3 实例

黄金坝YS108H1-01井为页岩气产能评价水平井，评价井段为2 762～4 115 m，储集层垂深2 531.88～ 2 546.69 m。射孔段岩石平均弹性模量为33 605 MPa，平均泊松比0.22，最小主应力约为57 MPa，最大主应力约为72 MPa，最大主应力方位为北西西—南东东向。该井采用分段多簇压裂，共分15段，每段长80～100 m，除第一段外，每段射孔3簇，平均簇间距为30 m。压后分析净压力约为10 MPa。

该井压裂中进行了地面微地震裂缝监测。微地震事件均发生于最大主应力方向，即裂缝沿最大主应力方向延伸，未发生明显偏转。该井1～6段压裂裂缝沿北东约120°发育，即沿最大主应力方向分布，裂缝平均高度约为50 m，平均半长约为300～400 m。模拟该井3簇同步裂缝扩展形态（见图9）。结果显示，裂缝基本沿直线扩展。模拟结果与微地震解释结果相符。裂缝呈直线扩展的主要原因是水平主应力差较大，抑制了裂缝转向。

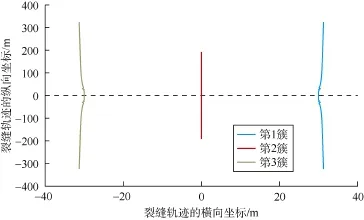
图9 YS108H1-01井3簇同步裂缝模拟结果

4 结论

基于位移不连续边界元法，建立了应力干扰计算模型，并与3D DDM和Olson模型对比，本文模型计算量远低于3D DDM，且裂缝宽度计算更符合实际，便于裂缝应力场和裂缝扩展的计算。

应力干扰作用范围受控于裂缝形态。对缝长大于缝高的裂缝，应力干扰作用范围为1.2～1.5倍缝高；对缝高大于缝长的裂缝，应力干扰作用范围为1.2～1.5倍缝长。

缝间距相对缝高越大或净压力相对原场主应力差越小，裂缝偏转角度越小，偏转位置距离井筒越远。裂缝最小可在距离井筒18.5 m处发生偏转，最大偏转角度为7.19°。

对于3簇压裂，等间距布缝时，外侧裂缝为主扩展裂缝，中间裂缝沿直线扩展；非等间距布缝时，裂缝扩展不均匀程度增大，距离其他裂缝均较远的外侧裂缝为主扩展裂缝，中间裂缝向与之间距较远的裂缝偏转。

实例分析表明，本文模型计算的裂缝扩展形态与现场监测结果相符，可用于施工设计和现场分析。

符号注释：

［1］ELBEL J L，MACK M G. Rrefracturing: Obervations and theories［R］. SPE 25464，1993.

［2］FISHER M K，HEINZE J R，HARRIS C D，et al. Optimizing horizontal completion techniques in the Barnett shale using microseismic fracture mapping［R］. SPE 90051，2004.

［3］吴奇，胥云，王腾飞，等. 增产改造理念的重大变革: 体积改造技术概论［J］. 天然气工业，2011，31（4）: 7-12. WU Qi，XU Yun，WANG Tengfei，et al. The resolution of reservoir stimulation: An introduction of volume fracturing［J］. Natural Gas Industry，2011，31（4）: 7-12.

［4］吴奇，胥云，王晓泉，等. 非常规油气藏体积改造技术: 内涵、优化设计与实现［J］. 石油勘探与开发，2012，39（3）: 252-258. WU Qi，XU Yun，WANG Xiaoquan，et al. Volume fracturing technology of unconventional reservoirs: Connotation，optimization design and implementation［J］. Petroleum Exploration and Development，2012，39（3）: 252-258.

［5］SNEDDON I N，ELLIOT H A. The opening of a Griffith crack under internal pressure［J］. Quart. Appl. Math.，1946，4（3）: 262-267.

［6］GREEN A E，SNEDDON I N. The distribution of stress in the neighborhood of a flat elliptical crack in an elastic solid［J］. Math. Proc. Cambridge Philos. Soc.，1950，46（1）: 159-163.

［7］POLLARD D D，HOLZHAUSEN G. On the mechanical interaction between a fluid-filled fracture and the earth's surface［J］. Tectonophysics，1979，53（1）: 27-57.

［8］王元淳. 边界元法基础［M］. 上海: 上海交通大学出版社，1988: 2-3. WANG Yuanchun. The basis of boundary element method［M］. Shanghai: Shanghai Jiaotong University Press，1988: 2-3.

［9］胡建伟，汤怀民. 微分方程数值方法［M］. 北京: 科学出版社，2007: 215-216. HU Jianwei，TANG Huaimin. Numerical methods of differential equations［M］. Beijing: Science Press，2007: 215-216.

［10］CROUCH S L. Solution of plane elasticity problems by the displacement discontinuity method. Ⅰ: Infinite body solution［J］. International Journal for Numerical Methods in Engineering，1976，10（2）: 301-343.

［11］SHOU K J. A higher order three-dimensional displacement discontinuity method with application to bonded half-space problems［D］. Minnesota: University of Minnesota，1993.

［12］OLSON J E. Predicting fracture swarms: The influence of subcritical crack growth and the crack-tip process zone on joint spacing in rock［J］. Journal of the Geological Society，2004，231（1）: 73-88.

［13］WENG X，KRESSE O，COHEN C，et al. Modeling of hydraulic fracture network propagation in a naturally fractured formation［R］. SPE 140253，2011.［14］WU Kan，OLSON J E. Simultaneous multifracture treatments: Fully coupled fluid flow and fracture mechanics for horizontal wells［R］. SPE 167626，2014.

［15］李世愚，和泰名，尹祥础，等. 岩石断裂力学导论［M］. 合肥: 中国科学技术大学出版社，2010: 45-46. LI Shiyu，HE Taiming，YIN Xiangchu，et al. Introduction of rock fracture mechnics［M］. Hefei: Press of University of Science and Technology of China，2010: 45-46.

［16］WARPINSKI N R，BRANAGAN P T. Altered-stress fracturing［J］. Journal of Petroleum Technology，1989，41（9）: 990-997.

［17］OLSON J E. Joint pattern development: Effects of subcritical crack growth and mechanical crack interaction［J］. Journal of Geophysical Research，1993，98（B7）: 12251-12265.

［18］ROUSSEL N P，SHARMA M M. Strategies to minimize frac spacing and stimulate natural fractures in horizontal completions［R］. SPE 146104，2011.

［19］OLSON J E. Multi-fracture propagation modeling: Applications to hydraulic fracturing in shales and tight gas sands［C］//The 42nd US rock mechanics symposium （USRMS）. San Francisco: American Rock Mechanics Association，2008.

［20］DETOURNAY E. Propagation regimes of fluid-driven fractures in impermeable rocks［J］. International Journal of Geomechanics，2004，41（35）: 35-45.

［21］POLLARD D D. Elementary fracture mechanics applied to the structural interpretation of dykes［R］. Halls: Geological Society of Canada，1987.

［22］张晓敏，万玲，严波，等. 断裂力学［M］. 北京: 清华大学出版社，2012: 76-77. ZHANG Xiaomin，WAN Ling，YAN Bo，et al. Fracture mechanics［M］. Beijing: Tsinghua University Press，2012: 76-77.

［23］SHEIBANI F，OLSON J. Stress intensity factor determination for three-dimensional crack using the displacement discontinuity method with applications to hydraulic fracture height growth and non-planar propagation paths［R］. Brisbane: International Society for Rock Mechanics，2013.

［24］马旭，郝瑞芬，来轩昂，等. 苏里格气田致密砂岩气藏水平井体积压裂矿场试验［J］. 石油勘探与开发，2014，41（6）: 742-747. MA Xu，HAO Ruifen，LAI Xuanang，et al. Field test of volume fracturing for horizontal wells in Sulige tight sandstone gas reservoirs［J］. Petroleum Exploration and Development，2014，41（6）: 742-747.

［25］ROUSSEL N P，SHARMA M M. Optimizing fracture spacing and sequencing in horizontal-well fracturing［J］. SPE Production & Operations，2011，26（2）: 173-184.

［26］吴奇，胥云，张守良，等. 非常规油气藏体积改造技术核心理论与优化设计关键［J］. 石油学报，2014，35（4）: 706-714. WU Qi，XU Yun，ZHANG Shouliang，et al. The core theories and key optimization of volume stimulation technology for unconventional reservoirs［J］. Acta Petrolei Sinica，2014，35（4）: 706-714.

（编辑 郭海莉）

Stress interference calculation model and its application in volume stimulation of horizontal wells

XU Yun1，2，CHEN Ming1，3，WU Qi2，4，LI Deqi5，YANG Nengyu4，WENG Dingwei1，2，GUAN Baoshan1，2
（1. Langfang Branch of PetroChina Research Institute of Petroleum Exploration & Development，Langfang 065007，China；2. The Key Laboratory of Research Stimulation，PetroChina，Langfang 065007，China； 3. PetroChina Research Institute of Petroleum Exploration & Development，Beijing 100083，China； 4. PetroChina Exploration and Production Company，Beijing 100007，China； 5. PetroChina Zhejiang Oilfield Company，Hangzhou 310023，China）

A new model for calculating stress fields of fractured media was established by incorporating stress correction factor based on displacement discontinuity boundary element method. The accuracy of the new model is close to 3D displacement discontinuity model，and its calculation is significantly simplified. An algorithm for multi-fracture propagation geometry was proposed based on fracture criterion and fracture growth rate law，which was used to investigate multi-fracture stress interference and propagation geometry. The results show that the size of stress interference is determined by the shortest dimension of fracture face，which is 1.2-1.5 times fracture height when fracture length is longer than fracture height，and 1.2-1.5 times fracture length when fracture length is shorter than fracture height. The larger the ratio of fracture spacing to fracture height，or the smaller the ratio of net pressure to the differential principle stress，the more close to well-bores the deviation position is，and the larger the deviation angle is. The middle fracture propagates to the fracture at a further distance and one dominating fracture propagates longest when three-cluster fractures are not equally spaced，while the middle fracture propagates straightly when three-cluster fractures are equally spaced.

horizontal well； volume fracturing； stress interference； displacement discontinuity method； fracture deviation；multi-fracture propagation； unequally distributed fracture

国家科技重大专项“大型油气田及煤层气开发”（2011ZX05013—003）

TE357.1

A

1000-0747（2016）05-0780-07

10.11698/PED.2016.05.14

胥云（1961-），男，重庆市人，博士，中国石油勘探开发研究院廊坊分院教授级高级工程师，主要从事油气藏压裂酸化基础理论、技术方法与现场应用等研究工作。地址：河北省廊坊市44号信箱，中国石油勘探开发研究院廊坊分院，邮政编码：065007。E-mail：xuyun69@petrochina.com.com

联系作者：陈铭（1990-）男，山东泰安人，中国石油勘探开发研究院硕士研究生，主要从事水力压裂数值模拟研究。地址：河北省廊坊市44号信箱，中国石油勘探开发研究院廊坊分院，邮政编码：065007。E-mail：xmcm0122@126.com

2015-11-21

2016-06-17